1022. Sum of Root To Leaf Binary Numbers

Given a binary tree, each node has value 0 or 1. Each root-to-leaf path represents a binary number starting with the most significant bit. For example, if the path is 0 -> 1 -> 1 -> 0 -> 1, then this could represent 01101 in binary, which is 13.
For all leaves in the tree, consider the numbers represented by the path from the root to that leaf.
Return the sum of these numbers.

Example 1: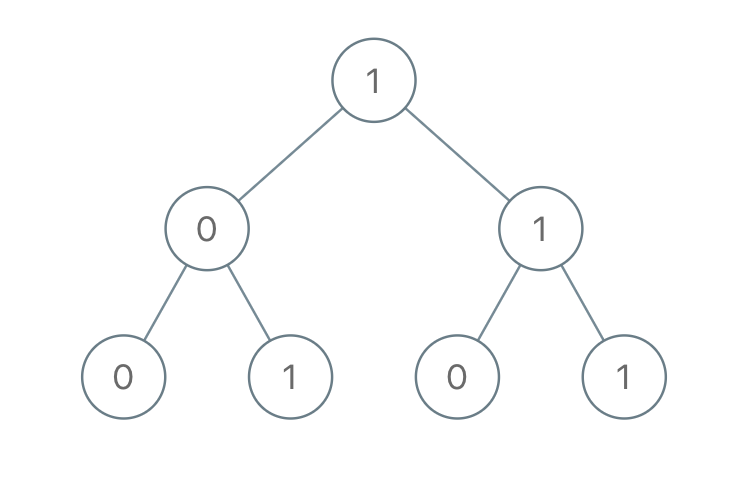

Input: [1,0,1,0,1,0,1]
Output: 22
Explanation: (100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22

Note:

1. The number of nodes in the tree is between 1 and 1000.
2. node.val is 0 or 1.
3. The answer will not exceed 2^31 - 1.

Runtime: 8 ms, faster than 60.81% of C++ online submissions for Sum of Root To Leaf Binary Numbers.
Memory Usage: 16.7 MB, less than 100.00% of C++ online submissions for Sum of Root To Leaf Binary Numbers.

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int sumRootToLeaf(TreeNode* root) {
        int sum = 0;
        traverse(root, sum, root->val);
        return sum;
    }
    void traverse(TreeNode* root, int& sum, int lastSum) {
        if (root->left != NULL) {
            traverse(root->left, sum, lastSum * 2 + root->left->val);
        }
        if (root->right != NULL) {
            traverse(root->right, sum, lastSum * 2 + root->right->val);
        }
        if (root->left == NULL && root->right == NULL) {
            sum += lastSum;
        }
    }
};