简介
R-B Tree,全称是Red-Black Tree,又称为“红黑树”,它一种特殊的二叉查找树。红黑树的每个节点上都有存储位表示节点的颜色,可以是红(Red)或黑(Black)。
红黑树的特性
(1)每个节点或者是黑色,或者是红色。
(2)根节点是黑色。
(3)每个叶子节点(NIL)是黑色。 [注意:这里叶子节点,是指为空(NIL或NULL)的叶子节点!]
(4)如果一个节点是红色的,则它的子节点必须是黑色的。
(5)从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。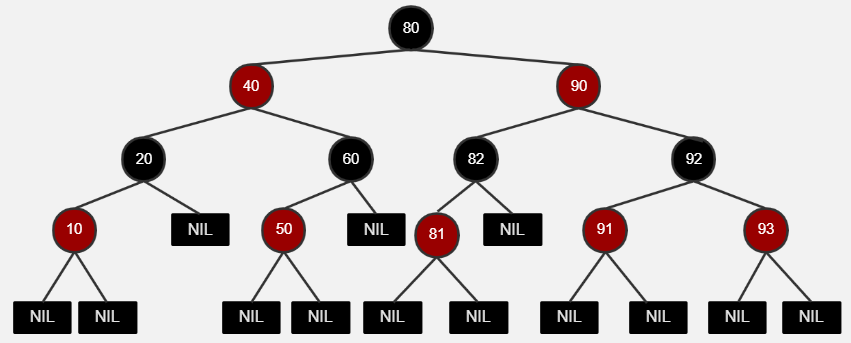
应用
红黑树的应用比较广泛,主要是用它来存储有序的数据,它的时间复杂度是O(lgn),效率非常之高。
例如,Java集合中的TreeSet和TreeMap,C++ STL中的set、map,以及Linux虚拟内存的管理,都是通过红黑树去实现的。
时间复杂度
红黑树的时间复杂度为: O(lgn)
定理:一棵含有n个节点的红黑树的高度至多为2log(n+1).
基本操作
红黑树的基本操作是添加、删除。在对红黑树进行添加或删除之后,都会用到旋转方法。为什么呢?道理很简单,添加或删除红黑树中的节点之后,红黑树就发生了变化,可能不满足红黑树的5条性质,也就不再是一颗红黑树了,而是一颗普通的树。而通过旋转,可以使这颗树重新成为红黑树。简单点说,旋转的目的是让树保持红黑树的特性。
旋转包括两种:左旋 和 右旋。下面分别对它们进行介绍。
左旋
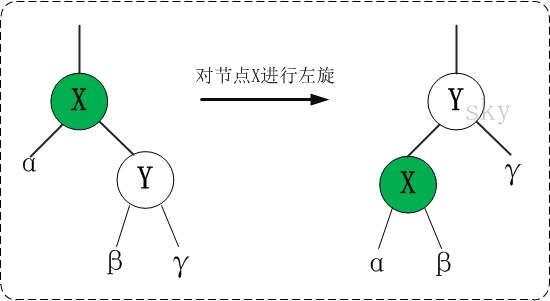
前提:这里假设x的右孩子为y。下面开始正式操作
- 将 “y的左孩子” 设为 “x的右孩子”,即 将β设为x的右孩子
- 将 “x” 设为 “y的左孩子的父亲”,即 将β的父亲设为x
- 将 “x的父亲” 设为 “y的父亲”
- 情况1:如果 “x的父亲” 是空节点,则将y设为根节点 0
- 情况2:如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子”
- 情况3:(x是它父节点的右孩子) 将y设为“x的父节点的右孩子”
- 将 “x” 设为 “y的左孩子” 、
- 将 “x的父节点” 设为 “y”

