布隆过滤器可以理解为一个不怎么精确的 set 结构，当你使用它的 contains 方法判断某 个对象是否存在时，它可能会误判。但是布隆过滤器也不是特别不精确，只要参数设置的合 理，它的精确度可以控制的相对足够精确，只会有小小的误判概率。
当布隆过滤器说某个值存在时，这个值可能不存在；当它说不存在时，那就肯定不存 在。

使用

布隆过滤器有二个基本指令，bf.add 添加元素，bf.exists 查询元素是否存在，它的用法 和 set 集合的 sadd 和 sismember 差不多。注意 bf.add 只能一次添加一个元素，如果想要
一次添加多个，就需要用到 bf.madd 指令。同样如果需要一次查询多个元素是否存在，就需
要用到 bf.mexists 指令。

  1. 127.0.0.1:6379> bf.add codehole user1
  2. (integer) 1
  3. 127.0.0.1:6379> bf.add codehole user2
  4. (integer) 1
  5. 127.0.0.1:6379> bf.add codehole user3
  6. (integer) 1
  7. 127.0.0.1:6379> bf.exists codehole user1
  8. (integer) 1
  9. 127.0.0.1:6379> bf.exists codehole user2
  10. (integer) 1
  11. 127.0.0.1:6379> bf.exists codehole user3
  12. (integer) 1
  13. 127.0.0.1:6379> bf.exists codehole user4
  14. (integer) 0
  15. 127.0.0.1:6379> bf.madd codehole user4 user5 user6
  16. 1) (integer) 1
  17. 2) (integer) 1
  18. 3) (integer) 1
  19. 127.0.0.1:6379> bf.mexists codehole user4 user5 user6 user7
  20. 1) (integer) 1
  21. 2) (integer) 1
  22. 3) (integer) 1
  23. 4) (integer) 0

误判率大约 1% 多点。你也许会问这个误判率还是有点高啊，有没有办法降低 一点？答案是有的。

我们上面使用的布隆过滤器只是默认参数的布隆过滤器，它在我们第一次 add 的时候自 动创建。Redis 其实还提供了自定义参数的布隆过滤器，需要我们在 add 之前使用 bf.reserve 指令显式创建。如果对应的 key 已经存在，bf.reserve 会报错。bf.reserve 有三个参数，分别是 key, error_rate 和 initial_size。错误率越低，需要的空间越大。initial_size 参数表示预计放 入的元素数量，当实际数量超出这个数值时，误判率会上升。
所以需要提前设置一个较大的数值避免超出导致误判率升高。如果不使用 bf.reserve，默 认的 error_rate 是 0.01，默认的 initial_size 是 100。

注意事项
布隆过滤器的 initial_size 估计的过大，会浪费存储空间，估计的过小，就会影响准确 率，用户在使用之前一定要尽可能地精确估计好元素数量，还需要加上一定的冗余空间以避 免实际元素可能会意外高出估计值很多。
布隆过滤器的 error_rate 越小，需要的存储空间就越大，对于不需要过于精确的场合， error_rate 设置稍大一点也无伤大雅。比如在新闻去重上而言，误判率高一点只会让小部分文 章不能让合适的人看到，文章的整体阅读量不会因为这点误判率就带来巨大的改变。

原理

image.png
每个布隆过滤器对应到 Redis 的数据结构里面就是一个大型的位数组和几个不一样的无 偏 hash 函数。所谓无偏就是能够把元素的 hash 值算得比较均匀。

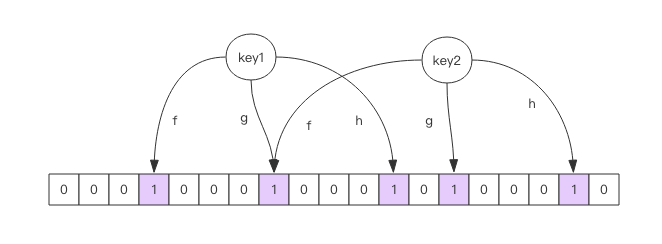
向布隆过滤器中添加 key 时，会使用多个 hash 函数对 key 进行 hash 算得一个整数索 引值然后对位数组长度进行取模运算得到一个位置，每个 hash 函数都会算得一个不同的位 置。再把位数组的这几个位置都置为 1 就完成了 add 操作。
向布隆过滤器询问 key 是否存在时，跟 add 一样，也会把 hash 的几个位置都算出 来，看看位数组中这几个位置是否都位 1，只要有一个位为 0，那么说明布隆过滤器中这个 key 不存在。如果都是 1，这并不能说明这个 key 就一定存在，只是极有可能存在，因为这 些位被置为 1 可能是因为其它的 key 存在所致。

空间占用估计

布隆过滤器有两个参数，第一个是预计元素的数量 n，第二个是错误率 f。公式根据这 两个输入得到两个输出，第一个输出是位数组的长度 l，也就是需要的存储空间大小 (bit)， 第二个输出是 hash 函数的最佳数量 k。hash 函数的数量也会直接影响到错误率，最佳的数量会有最低的错误率。

  1. k=0.7*(l/n) # 约等于
  3. f=0.6185^(l/n) # ^ 表示次方计算，也就是 math.pow

从公式中可以看出
1、位数组相对越长 (l/n)，错误率 f 越低，这个和直观上理解是一致的
2、位数组相对越长 (l/n)，hash 函数需要的最佳数量也越多，影响计算效率
3、当一个元素平均需要 1 个字节 (8bit) 的指纹空间时 (l/n=8)，错误率大约为 2%
4、错误率为 10%，一个元素需要的平均指纹空间为 4.792 个 bit，大约为 5bit
5、错误率为 1%，一个元素需要的平均指纹空间为 9.585 个 bit，大约为 10bit
6、错误率为 0.1%，一个元素需要的平均指纹空间为 14.377 个 bit，大约为 15bit

应用

在爬虫系统中，我们需要对 URL 进行去重，已经爬过的网页就可以不用爬了。但是 URL 太多了，几千万几个亿，如果用一个集合装下这些 URL 地址那是非常浪费空间的。这 时候就可以考虑使用布隆过滤器。它可以大幅降低去重存储消耗，只不过也会使得爬虫系统 错过少量的页面。

布隆过滤器在 NoSQL 数据库领域使用非常广泛，我们平时用到的 HBase、Cassandra 还有 LevelDB、RocksDB 内部都有布隆过滤器结构，布隆过滤器可以显著降低数据库的 IO 请求数量。当用户来查询某个 row 时，可以先通过内存中的布隆过滤器过滤掉大量不存在的 row 请求，然后再去磁盘进行查询。

邮箱系统的垃圾邮件过滤功能也普遍用到了布隆过滤器，因为用了这个过滤器，所以平 时也会遇到某些正常的邮件被放进了垃圾邮件目录中，这个就是误判所致，概率很低。