N皇后

Ref: https://pdai.tech/md/algorithm/alg-core-backtracking.html#n-%E7%9A%87%E5%90%8E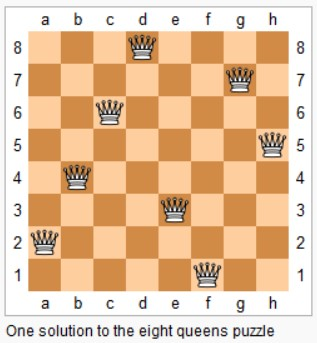

在 n*n 的矩阵中摆放 n 个皇后，并且每个皇后不能在同一行，同一列，同一对角线上，求所有的 n 皇后的解。
一行一行地摆放，在确定一行中的那个皇后应该摆在哪一列时，需要用三个标记数组来确定某一列是否合法，这三个标记数组分别为：列标记数组、45 度对角线标记数组和 135 度对角线标记数组。

45 度对角线标记数组的维度为 2 n - 1，通过下图可以明确 (r, c) 的位置所在的数组下标为 r + c: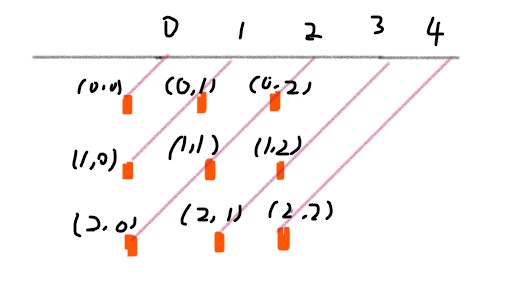

135 度对角线标记数组的维度也是 2 n - 1，(r, c) 的位置所在的数组下标为 n - 1 - (r - c):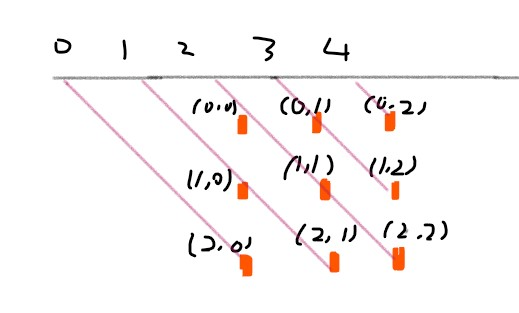

private List<List<String>> solutions;
private char[][] nQueens;
private boolean[] colUsed;
private boolean[] diagonals45Used;
private boolean[] diagonals135Used;
private int n;
public List<List<String>> solveNQueens(int n) {
    solutions = new ArrayList<>();
    nQueens = new char[n][n];
    for (int i = 0; i < n; i++) {
        Arrays.fill(nQueens[i], '.');
    }
    colUsed = new boolean[n];
    diagonals45Used = new boolean[2 * n - 1];
    diagonals135Used = new boolean[2 * n - 1];
    this.n = n;
    backtracking(0);
    return solutions;
}
private void backtracking(int row) {
    if (row == n) {
        List<String> list = new ArrayList<>();
        for (char[] chars : nQueens) {
            list.add(new String(chars));
        }
        solutions.add(list);
        return;
    }
    for (int col = 0; col < n; col++) {
        int diagonals45Idx = row + col;
        int diagonals135Idx = n - 1 - (row - col);
        if (colUsed[col] || diagonals45Used[diagonals45Idx] || diagonals135Used[diagonals135Idx]) {
            continue;
        }
        nQueens[row][col] = 'Q';
        colUsed[col] = diagonals45Used[diagonals45Idx] = diagonals135Used[diagonals135Idx] = true;
        backtracking(row + 1);
        colUsed[col] = diagonals45Used[diagonals45Idx] = diagonals135Used[diagonals135Idx] = false;
        nQueens[row][col] = '.';
    }
}