Ref: https://blog.csdn.net/lb812913059/article/details/83313360

1.二叉树遍历

二叉树的深度优先遍历的非递归的通用做法是采用栈，广度优先遍历的非递归的通用做法是采用队列。

1.1 深度优先遍历

对每一个可能的分支路径深入到不能再深入为止，而且每个结点只能访问一次。对每一个可能的分支路径深入到不能再深入为止，而且每个结点只能访问一次。
要特别注意的是，二叉树的深度优先遍历比较特殊，可以细分为先序遍历、中序遍历、后序遍历。具体说明如下：

先序遍历：对任一子树，先访问根，然后遍历其左子树，最后遍历其右子树。
中序遍历：对任一子树，先遍历其左子树，然后访问根，最后遍历其右子树。
后序遍历：对任一子树，先遍历其左子树，然后遍历其右子树，最后访问根。

Java 循环实现先序遍历：

  1. public void flatten(TreeNode root) {
  2.     List<TreeNode> list = new ArrayList<TreeNode>();
  3.     Deque<TreeNode> stack = new LinkedList<TreeNode>();
  4.     TreeNode node = root;
  5.     while (node != null || !stack.isEmpty()) {
  6.         while (node != null) {
  7.             list.add(node);
  8.             stack.push(node);
  9.             node = node.left;
  10.         }
  11.         node = stack.pop();
  12.         node = node.right;
  13.     }
  14. }

1.2 广度优先遍历

又叫层次遍历，从上往下对每一层依次访问，在每一层中，从左往右（也可以从右往左）访问结点，访问完一层就进入下一层，直到没有结点可以访问为止。又叫层次遍历，从上往下对每一层依次访问，在每一层中，从左往右（也可以从右往左）访问结点，访问完一层就进入下一层，直到没有结点可以访问为止。

1.3 深度优先搜索算法

不全部保留结点，占用空间少；有回溯操作 (即有入栈、出栈操作)，运行速度慢。
通常深度优先搜索法不全部保留结点，扩展完的结点从数据库中弹出删去，这样，一般在数据库中存储的结点数就是深度值，因此它占用空间较少。所以，当搜索树的结点较多，用其它方法易产生内存溢出时，深度优先搜索不失为一种有效的求解方法。

1.4 广度优先搜索算法

保留全部结点，占用空间大； 无回溯操作 (即无入栈、出栈操作)，运行速度快。
广度优先搜索算法，一般需存储产生的所有结点，占用的存储空间要比深度优先搜索大得多，因此，程序设计中，必须考虑溢出和节省内存空间的问题。但广度优先搜索法一般无回溯操作，即入栈和出栈的操作，所以运行速度比深度优先搜索要快些。

1.5 案例

image.png
先序遍历（递归）：35 20 15 16 29 28 30 40 50 45 55
中序遍历（递归）：15 16 20 28 29 30 35 40 45 50 55
后序遍历（递归）：16 15 28 30 29 20 45 55 50 40 35

广度优先遍历：35 20 40 15 29 50 16 28 30 45 55
深度优先遍历：16 15 28 30 29 20 45 55 50 40 35

2.深度优先遍历

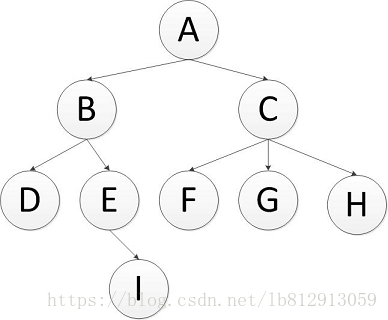
image.png
对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次。
对于上面的例子来说深度优先遍历的结果就是：A,B,D,E,I,C,F,G,H.(假设先走子节点的的左侧)。

深度优先遍历各个节点，需要使用到栈（Stack）这种数据结构。stack 的特点是是先进后出。整个遍历过程如下：

  1. 首先将A节点压入栈中，stack（A）;
  2. 将A节点弹出，同时将A的子节点C，B压入栈中，此时B在栈的顶部，stack(B,C)；
  3. 将B节点弹出，同时将B的子节点E，D压入栈中，此时D在栈的顶部，stack（D,E,C）；
  4. 将D节点弹出，没有子节点压入,此时E在栈的顶部，stack（E，C）；
  5. 将E节点弹出，同时将E的子节点I压入，stack（I,C）；
  6. ...依次往下，最终遍历完成

代码：

  1. public class TreeNode {
  2.     int val = 0;
  3.     TreeNode left = null;
  4.     TreeNode right = null;
  6.     public TreeNode(int val) {
  7.         this.val = val;
  8.     }
  9. }
  10. public class Solution {
  11.     public ArrayList<Integer> deep(TreeNode root) {
  12.         ArrayList<Integer> lists=new ArrayList<Integer>();
  13.         if(root==null)
  14.             return lists;
  15.         Stack<TreeNode> stack=new Stack<TreeNode>();
  16.         stack.push(root);
  17.         while(!stack.isEmpty()){
  18.             TreeNode node=stack.pop();
  19. 　　　　　　//先往栈中压入右节点，再压左节点，这样出栈就是先左节点后右节点了。
  20.             if(node.right!=null)
  21.                 stack.push(tree.right);
  22.             if(node.left!=null)
  23.                 stack.push(tree.left);
  24.             lists.add(node.val);
  25.         }
  26.         return lists;
  27.     }
  28. }

3.广度优先遍历

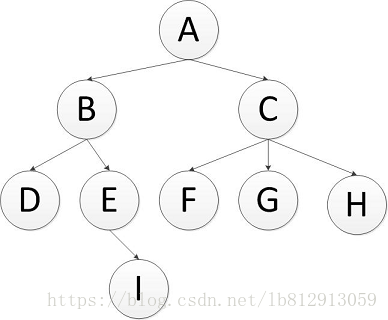
image.png
其过程检验来说是对每一层节点依次访问，访问完一层进入下一层，而且每个节点只能访问一次。对于上面的例子来说，广度优先遍历的 结果是：A,B,C,D,E,F,G,H,I (假设每层节点从左到右访问)。

广度优先遍历各个节点，需要使用到队列（Queue）这种数据结构，queue 的特点是先进先出，其实也可以使用双端队列，区别就是双端队列首位都可以插入和弹出节点。整个遍历过程如下：

  1. 首先将A节点插入队列中，queue（A）;
  2. 将A节点弹出，同时将A的子节点B，C插入队列中，此时B在队列首，C在队列尾部，queue（B，C）；
  3. 将B节点弹出，同时将B的子节点D，E插入队列中，此时C在队列首，E在队列尾部，queue（C，D，E）;
  4. 将C节点弹出，同时将C的子节点F，G，H插入队列中，此时D在队列首，H在队列尾部，queue（D，E，F，G，H）；
  5. 将D节点弹出，D没有子节点，此时E在队列首，H在队列尾部，queue（E，F，G，H）；
  6. ...依次往下，最终遍历完成

代码：

  1. public class TreeNode {
  2.     int val = 0;
  3.     TreeNode left = null;
  4.     TreeNode right = null;
  6.     public TreeNode(int val) {
  7.         this.val = val;
  8.     }
  9. }
  10. public class Solution {
  11.     public ArrayList<Integer> wide(TreeNode root) {
  12.         ArrayList<Integer> lists=new ArrayList<Integer>();
  13.         if(root==null)
  14.             return lists;
  15.         Queue<TreeNode> queue=new LinkedList<TreeNode>();
  16.         queue.offer(root);
  17.         while(!queue.isEmpty()){
  18.             TreeNode node = queue.poll();
  19.             if(node.left!=null){
  20.                 queue.offer(node.left);
  21.             }
  22.             if(node.right!=null){
  23.                 queue.offer(node.right);
  24.             }
  25.             lists.add(node.val);
  26.         }
  27.         return lists;
  28.     }
  29. }