Ref: https://mp.weixin.qq.com/s/vn3KiV-ez79FmbZ36SX9lg

1.概览

排序算法可以分为内部排序和外部排序。
内部排序是数据记录在内存中进行排序。
而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。
常见的内部排序算法有：插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。
用一张图概括：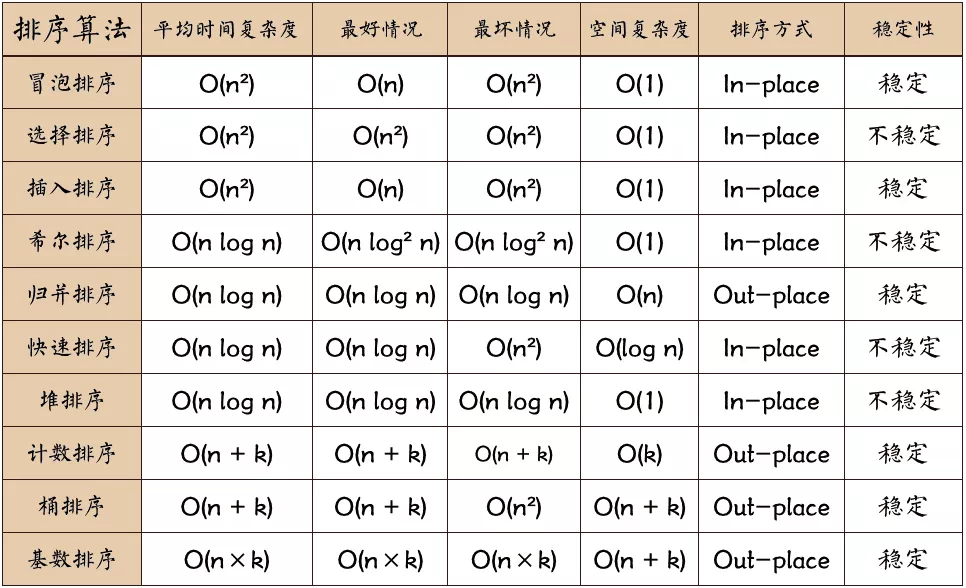
image.png

关于时间复杂度：
平方阶 (O (n2)) 排序 各类简单排序：直接插入、直接选择和冒泡排序。
线性对数阶 (O (nlog2n)) 排序 快速排序、堆排序和归并排序；
O (n1+§)) 排序，§ 是介于 0 和 1 之间的常数。 希尔排序
线性阶 (O (n)) 排序 基数排序，此外还有桶、箱排序。

关于稳定性：
稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序。
不是稳定的排序算法：选择排序、快速排序、希尔排序、堆排序。

2.排序算法

2.1 选择排序

算法步骤

  • 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
  • 再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
  • 重复第二步，直到所有元素均排序完毕。

动画演示
image.png
代码：

  1. public class SelectionSort implements IArraySort {
  3.     @Override
  4.     public int[] sort(int[] sourceArray) throws Exception {
  5.         int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
  7.         // 总共要经过 N-1 轮比较
  8.         for (int i = 0; i < arr.length - 1; i++) {
  9.             int min = i;
  11.             // 每轮需要比较的次数 N-i
  12.             for (int j = i + 1; j < arr.length; j++) {
  13.                 if (arr[j] < arr[min]) {
  14.                     // 记录目前能找到的最小值元素的下标
  15.                     min = j;
  16.                 }
  17.             }
  19.             // 将找到的最小值和i位置所在的值进行交换
  20.             if (i != min) {
  21.                 int tmp = arr[i];
  22.                 arr[i] = arr[min];
  23.                 arr[min] = tmp;
  24.             }
  26.         }
  27.         return arr;
  28.     }
  29. }

2.2 选择排序

算法步骤：

  • 将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。
  • 从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）

动画演示：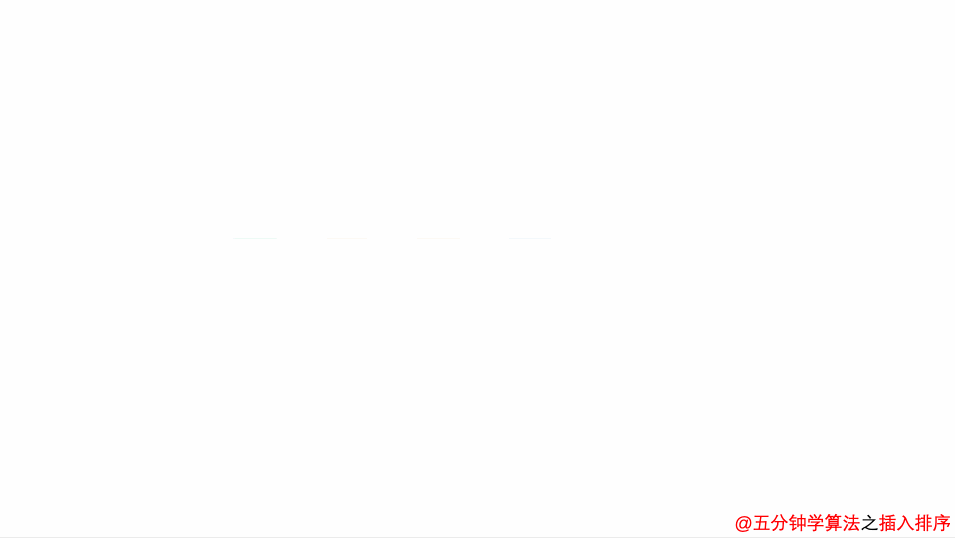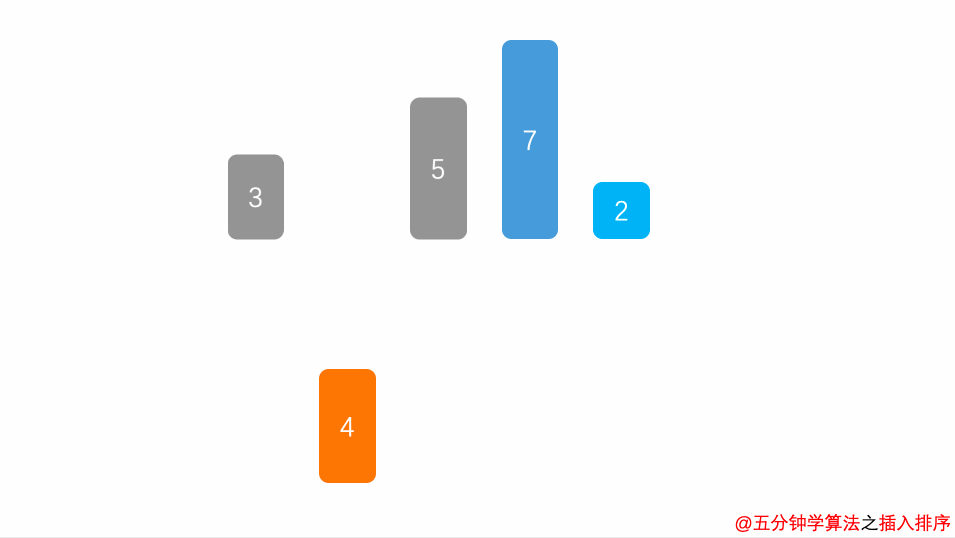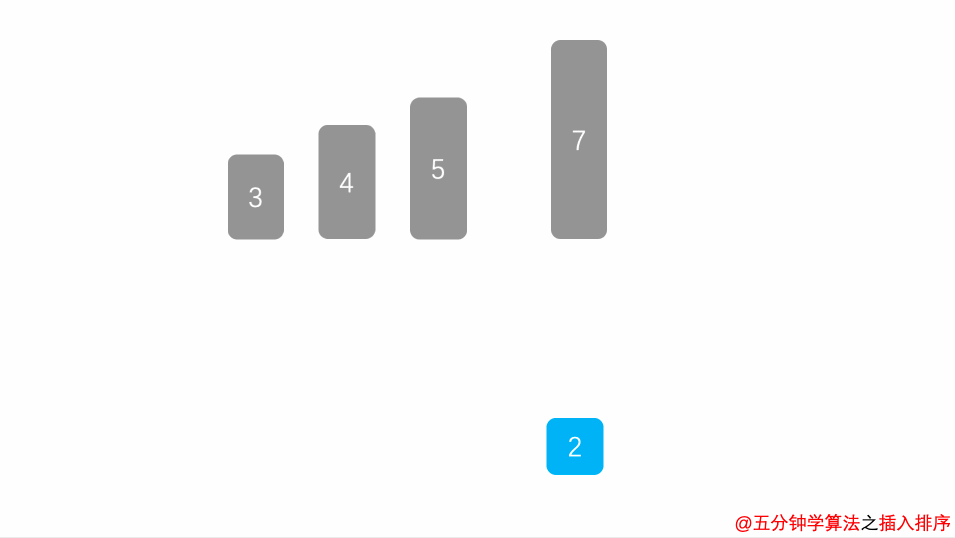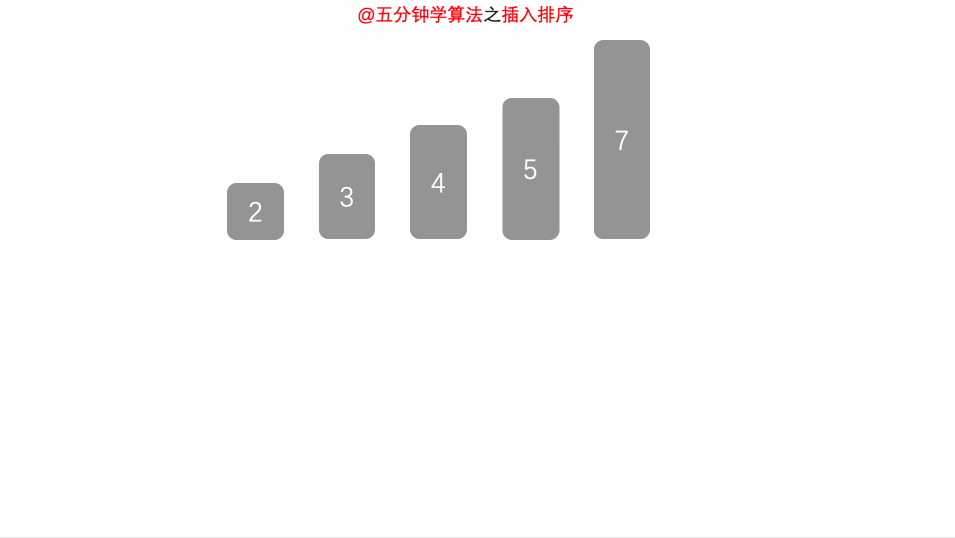
排序算法 - 图3
代码：

  1. public class InsertSort implements IArraySort {
  3.     @Override
  4.     public int[] sort(int[] sourceArray) throws Exception {
  5.         // 对 arr 进行拷贝，不改变参数内容
  6.         int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
  8.         // 从下标为1的元素开始选择合适的位置插入，因为下标为0的只有一个元素，默认是有序的
  9.         for (int i = 1; i < arr.length; i++) {
  11.             // 记录要插入的数据
  12.             int tmp = arr[i];
  14.             // 从已经排序的序列最右边的开始比较，找到比其小的数
  15.             int j = i;
  16.             while (j > 0 && tmp < arr[j - 1]) {
  17.                 arr[j] = arr[j - 1];
  18.                 j--;
  19.             }
  21.             // 存在比其小的数，插入
  22.             if (j != i) {
  23.                 arr[j] = tmp;
  24.             }
  26.         }
  27.         return arr;
  28.     }
  29. }

2.3 归并排序

算法步骤：

  • 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；
  • 设定两个指针，最初位置分别为两个已经排序序列的起始位置；
  • 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；
  • 重复步骤 3 直到某一指针达到序列尾；
  • 将另一序列剩下的所有元素直接复制到合并序列尾。

动画演示：
排序算法 - 图4
代码：

  1. public class MergeSort implements IArraySort {
  3.     @Override
  4.     public int[] sort(int[] sourceArray) throws Exception {
  5.         // 对 arr 进行拷贝，不改变参数内容
  6.         int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
  8.         if (arr.length < 2) {
  9.             return arr;
  10.         }
  11.         int middle = (int) Math.floor(arr.length / 2);
  13.         int[] left = Arrays.copyOfRange(arr, 0, middle);
  14.         int[] right = Arrays.copyOfRange(arr, middle, arr.length);
  16.         return merge(sort(left), sort(right));
  17.     }
  19.     protected int[] merge(int[] left, int[] right) {
  20.         int[] result = new int[left.length + right.length];
  21.         int i = 0;
  22.         while (left.length > 0 && right.length > 0) {
  23.             if (left[0] <= right[0]) {
  24.                 result[i++] = left[0];
  25.                 left = Arrays.copyOfRange(left, 1, left.length);
  26.             } else {
  27.                 result[i++] = right[0];
  28.                 right = Arrays.copyOfRange(right, 1, right.length);
  29.             }
  30.         }
  32.         while (left.length > 0) {
  33.             result[i++] = left[0];
  34.             left = Arrays.copyOfRange(left, 1, left.length);
  35.         }
  37.         while (right.length > 0) {
  38.             result[i++] = right[0];
  39.             right = Arrays.copyOfRange(right, 1, right.length);
  40.         }
  42.         return result;
  43.     }
  45. }


2.4 快速排序

算法步骤：

  • 从数列中挑出一个元素，称为 “基准”（pivot）;
  • 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
  • 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；

动画演示：
排序算法 - 图5
代码：

  1. public class QuickSort implements IArraySort {
  3.     @Override
  4.     public int[] sort(int[] sourceArray) throws Exception {
  5.         // 对 arr 进行拷贝，不改变参数内容
  6.         int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
  8.         return quickSort(arr, 0, arr.length - 1);
  9.     }
  11.     private int[] quickSort(int[] arr, int left, int right) {
  12.         if (left < right) {
  13.             int partitionIndex = partition(arr, left, right);
  14.             quickSort(arr, left, partitionIndex - 1);
  15.             quickSort(arr, partitionIndex + 1, right);
  16.         }
  17.         return arr;
  18.     }
  20.     private int partition(int[] arr, int left, int right) {
  21.         // 设定基准值（pivot）
  22.         int pivot = left;
  23.         int index = pivot + 1;
  24.         for (int i = index; i <= right; i++) {
  25.             if (arr[i] < arr[pivot]) {
  26.                 swap(arr, i, index);
  27.                 index++;
  28.             }
  29.         }
  30.         swap(arr, pivot, index - 1);
  31.         return index - 1;
  32.     }
  34.     private void swap(int[] arr, int i, int j) {
  35.         int temp = arr[i];
  36.         arr[i] = arr[j];
  37.         arr[j] = temp;
  38.     }
  40. }


2.5 堆排序

算法步骤：

  • 创建一个堆 H [0……n-1]；
  • 把堆首（最大值）和堆尾互换；
  • 把堆的尺寸缩小 1，并调用 shift_down (0)，目的是把新的数组顶端数据调整到相应位置；
  • 重复步骤 2，直到堆的尺寸为 1。

动画演示：
排序算法 - 图6
代码：

  1. public class HeapSort implements IArraySort {
  3.     @Override
  4.     public int[] sort(int[] sourceArray) throws Exception {
  5.         // 对 arr 进行拷贝，不改变参数内容
  6.         int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
  8.         int len = arr.length;
  10.         buildMaxHeap(arr, len);
  12.         for (int i = len - 1; i > 0; i--) {
  13.             swap(arr, 0, i);
  14.             len--;
  15.             heapify(arr, 0, len);
  16.         }
  17.         return arr;
  18.     }
  20.     private void buildMaxHeap(int[] arr, int len) {
  21.         for (int i = (int) Math.floor(len / 2); i >= 0; i--) {
  22.             heapify(arr, i, len);
  23.         }
  24.     }
  26.     private void heapify(int[] arr, int i, int len) {
  27.         int left = 2 * i + 1;
  28.         int right = 2 * i + 2;
  29.         int largest = i;
  31.         if (left < len && arr[left] > arr[largest]) {
  32.             largest = left;
  33.         }
  35.         if (right < len && arr[right] > arr[largest]) {
  36.             largest = right;
  37.         }
  39.         if (largest != i) {
  40.             swap(arr, i, largest);
  41.             heapify(arr, largest, len);
  42.         }
  43.     }
  45.     private void swap(int[] arr, int i, int j) {
  46.         int temp = arr[i];
  47.         arr[i] = arr[j];
  48.         arr[j] = temp;
  49.     }
  51. }

2.6 桶排序

算法步骤：

  • 设置固定数量的空桶。
  • 把数据放到对应的桶中。
  • 对每个不为空的桶中数据进行排序。
  • 拼接不为空的桶中数据，得到结果

动画演示：
排序算法 - 图7
代码：

  1. public class BucketSort implements IArraySort {
  3.     private static final InsertSort insertSort = new InsertSort();
  5.     @Override
  6.     public int[] sort(int[] sourceArray) throws Exception {
  7.         // 对 arr 进行拷贝，不改变参数内容
  8.         int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
  10.         return bucketSort(arr, 5);
  11.     }
  13.     private int[] bucketSort(int[] arr, int bucketSize) throws Exception {
  14.         if (arr.length == 0) {
  15.             return arr;
  16.         }
  18.         int minValue = arr[0];
  19.         int maxValue = arr[0];
  20.         for (int value : arr) {
  21.             if (value < minValue) {
  22.                 minValue = value;
  23.             } else if (value > maxValue) {
  24.                 maxValue = value;
  25.             }
  26.         }
  28.         int bucketCount = (int) Math.floor((maxValue - minValue) / bucketSize) + 1;
  29.         int[][] buckets = new int[bucketCount][0];
  31.         // 利用映射函数将数据分配到各个桶中
  32.         for (int i = 0; i < arr.length; i++) {
  33.             int index = (int) Math.floor((arr[i] - minValue) / bucketSize);
  34.             buckets[index] = arrAppend(buckets[index], arr[i]);
  35.         }
  37.         int arrIndex = 0;
  38.         for (int[] bucket : buckets) {
  39.             if (bucket.length <= 0) {
  40.                 continue;
  41.             }
  42.             // 对每个桶进行排序，这里使用了插入排序
  43.             bucket = insertSort.sort(bucket);
  44.             for (int value : bucket) {
  45.                 arr[arrIndex++] = value;
  46.             }
  47.         }
  49.         return arr;
  50.     }
  52.     /**
  53.      * 自动扩容，并保存数据
  54.      *
  55.      * @param arr
  56.      * @param value
  57.      */
  58.     private int[] arrAppend(int[] arr, int value) {
  59.         arr = Arrays.copyOf(arr, arr.length + 1);
  60.         arr[arr.length - 1] = value;
  61.         return arr;
  62.     }
  64. }

2.7 基数排序

算法步骤：

  • 将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零
  • 从最低位开始，依次进行一次排序
  • 从最低位排序一直到最高位排序完成以后，数列就变成一个有序序列

动画演示：
排序算法 - 图8
代码：

  1. public class RadixSort implements IArraySort {
  3.     @Override
  4.     public int[] sort(int[] sourceArray) throws Exception {
  5.         // 对 arr 进行拷贝，不改变参数内容
  6.         int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
  8.         int maxDigit = getMaxDigit(arr);
  9.         return radixSort(arr, maxDigit);
  10.     }
  12.     /**
  13.      * 获取最高位数
  14.      */
  15.     private int getMaxDigit(int[] arr) {
  16.         int maxValue = getMaxValue(arr);
  17.         return getNumLenght(maxValue);
  18.     }
  20.     private int getMaxValue(int[] arr) {
  21.         int maxValue = arr[0];
  22.         for (int value : arr) {
  23.             if (maxValue < value) {
  24.                 maxValue = value;
  25.             }
  26.         }
  27.         return maxValue;
  28.     }
  30.     protected int getNumLenght(long num) {
  31.         if (num == 0) {
  32.             return 1;
  33.         }
  34.         int lenght = 0;
  35.         for (long temp = num; temp != 0; temp /= 10) {
  36.             lenght++;
  37.         }
  38.         return lenght;
  39.     }
  41.     private int[] radixSort(int[] arr, int maxDigit) {
  42.         int mod = 10;
  43.         int dev = 1;
  45.         for (int i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
  46.             // 考虑负数的情况，这里扩展一倍队列数，其中 [0-9]对应负数，[10-19]对应正数 (bucket + 10)
  47.             int[][] counter = new int[mod * 2][0];
  49.             for (int j = 0; j < arr.length; j++) {
  50.                 int bucket = ((arr[j] % mod) / dev) + mod;
  51.                 counter[bucket] = arrayAppend(counter[bucket], arr[j]);
  52.             }
  54.             int pos = 0;
  55.             for (int[] bucket : counter) {
  56.                 for (int value : bucket) {
  57.                     arr[pos++] = value;
  58.                 }
  59.             }
  60.         }
  62.         return arr;
  63.     }
  64.     private int[] arrayAppend(int[] arr, int value) {
  65.         arr = Arrays.copyOf(arr, arr.length + 1);
  66.         arr[arr.length - 1] = value;
  67.         return arr;
  68.     }
  69. }