Ref: https://pdai.tech/md/algorithm/alg-core-dynamic.html#0-1-%E8%83%8C%E5%8C%85

概览

0-1 背包：

完全背包：

  • 1449. 数位成本和为目标值的最大数字
  • 322. 零钱兑换
  • 518. 零钱兑换 II

  • 279. 完全平方数

    0-1背包

    有一个容量为 N 的背包，要用这个背包装下物品的价值最大，这些物品有两个属性：体积 w 和价值 v。 定义一个二维数组 dp 存储最大价值，其中 dp[i][j] 表示前 i 件物品体积不超过 j 的情况下能达到的最大价值。
    设第 i 件物品体积为 w，价值为 v，根据第 i 件物品是否添加到背包中，可以分两种情况讨论:

  • 第 i 件物品没添加到背包，总体积不超过 j 的前 i 件物品的最大价值就是总体积不超过 j 的前 i-1 件物品的最大价值，dp[i][j] = dp[i-1][j]。

  • 第 i 件物品添加到背包中，dp [i][j] = dp [i-1][j-w] + v。 第 i 件物品可添加也可以不添加，取决于哪种情况下最大价值更大。

因此，0-1 背包的状态转移方程为: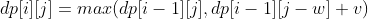
image.png

  1. public int knapsack(int W, int N, int[] weights, int[] values) {
  2.     int[][] dp = new int[N + 1][W + 1];
  3.     for (int i = 1; i <= N; i++) {
  4.         int w = weights[i - 1], v = values[i - 1];
  5.         for (int j = 1; j <= W; j++) {
  6.             if (j >= w) {
  7.                 dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - w] + v);
  8.             } else {
  9.                 dp[i][j] = dp[i - 1][j];
  10.             }
  11.         }
  12.     }
  13.     return dp[N][W];
  14. }

空间优化

在程序实现时可以对 0-1 背包做优化。观察状态转移方程可以知道，前 i 件物品的状态仅与前 i-1 件物品的状态有关，因此可以将 dp 定义为一维数组，其中 dp [j] 既可以表示 dp [i-1][j] 也可以表示 dp [i][j]。此时，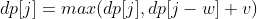
背包 - 图2
因为 dp [j-w] 表示 dp [i-1][j-w]，因此不能先求 dp [i][j-w]，以防将 dp [i-1][j-w] 覆盖。也就是说要先计算 dp[i][j] 再计算 dp[i][j-w]，在程序实现时需要按倒序来循环求解。

  1. public int knapsack(int W, int N, int[] weights, int[] values) {
  2.     int[] dp = new int[W + 1];
  3.     for (int i = 1; i <= N; i++) {
  4.         int w = weights[i - 1], v = values[i - 1];
  5.         for (int j = W; j >= 1; j--) {
  6.             if (j >= w) {
  7.                 dp[j] = Math.max(dp[j], dp[j - w] + v);
  8.             }
  9.         }
  10.     }
  11.     return dp[W];
  12. }

数组等和子数组

Ref: Leetcode
image.png
在前 i 个元素里找到和为 target 的元素：
image.png
上一行的结果可以直接抄下来，因为和为 target 的元素之前就存在的话，则一直存在，下一行只不过增加了元素。

  1. class Solution {
  2.     public boolean canPartition(int[] nums) {
  3.         int len = nums.length;
  4.         if (len == 1) {
  5.             return false;
  6.         }
  7.         int sum = 0;
  8.         for (int n : nums) {
  9.             sum += n;
  10.         }
  12.         if ((sum & 1) == 1) {
  13.             return false;
  14.         }
  16.         int target = sum / 2;
  17.         boolean[] dp = new boolean[target + 1];
  18.         dp[0] = true;
  20.         for (int i = 0; i < len; i++) {
  21.             for (int j = target; j >= 0 && nums[i] <= j; j--) {
  22.                 dp[j] = dp[j] || dp[j - nums[i]];
  23.             }
  24.             if (dp[target]) {
  25.                 return true;
  26.             }
  27.         }
  28.         return dp[target];
  29.     }
  30. }

和为 K 的子数组

Ref: Leetcode
给你一个整数数组 nums 和一个整数 k ，请你统计并返回该数组中和为 k 的连续子数组的个数。
输入：nums = [1,1,1], k = 2 输出：2
输入：nums = [1,2,3], k = 3 输出：2
image.png

  1. class Solution {
  2.     public int subarraySum(int[] nums, int k) {
  4.         int len = nums.length;
  6.         Map<Integer, Integer> map = new HashMap<>();
  8.         int count = 0, pre = 0;
  9.         map.put(0, 1);
  10.         for (int i = 0; i < len; i++) {
  11.             pre += nums[i];
  13.             if (map.containsKey(pre - k)) {
  14.                 count += map.get(pre - k);
  15.             }
  17.             map.put(pre, map.getOrDefault(pre, 0) + 1);
  18.         }
  20.         return count;
  21.     }
  22. }

目标和

方法二：动态规划
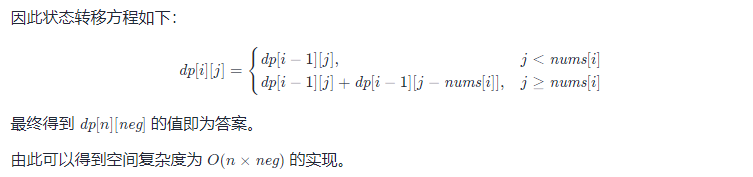
image.png
image.png

  1. class Solution {
  2.     public int findTargetSumWays(int[] nums, int target) {
  3.         int sum = 0;
  4.         for (int num : nums) {
  5.             sum += num;
  6.         }
  7.         int diff = sum - target;
  8.         if (diff < 0 || diff % 2 != 0) {
  9.             return 0;
  10.         }
  11.         int n = nums.length, neg = diff / 2;
  12.         int[][] dp = new int[n + 1][neg + 1];
  13.         dp[0][0] = 1;
  14.         for (int i = 1; i <= n; i++) {
  15.             int num = nums[i - 1];
  16.             for (int j = 0; j <= neg; j++) {
  17.                 dp[i][j] = dp[i - 1][j];
  18.                 if (j >= num) {
  19.                     dp[i][j] += dp[i - 1][j - num];
  20.                 }
  21.             }
  22.         }
  23.         return dp[n][neg];
  24.     }
  25. }

最多的字符串（背包 - 多维费用）

字符组成最多的字符串

  1. 输入：strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
  2. 输出：4
  3. 解释：最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ，因此答案是 4 。
  4. 其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。

这是一个多维费用的 0-1 背包问题，有两个背包大小，0 的数量和 1 的数量。

  1. public int findMaxForm(String[] strs, int m, int n) {
  2.     if (strs == null || strs.length == 0) {
  3.         return 0;
  4.     }
  5.     int[][] dp = new int[m + 1][n + 1];
  6.     for (String s : strs) {    // 每个字符串只能用一次
  7.         int ones = 0, zeros = 0;
  8.         for (char c : s.toCharArray()) {
  9.             if (c == '0') {
  10.                 zeros++;
  11.             } else {
  12.                 ones++;
  13.             }
  14.         }
  15.         for (int i = m; i >= zeros; i--) {
  16.             for (int j = n; j >= ones; j--) {
  17.                 dp[i][j] = Math.max(dp[i][j], dp[i - zeros][j - ones] + 1);
  18.             }
  19.         }
  20.     }
  21.     return dp[m][n];
  22. }

零钱兑换（完全背包 - 组合）

输入：coins = [1, 2, 5], amount = 11
输出：3 
解释：11 = 5 + 5 + 1

image.png

public int coinChange(int[] coins, int amount) {
    int len = coins.length;
    int[] dp = new int[amount + 1];
    Arrays.fill(dp, amount + 1);
    dp[0] = 0;

    for (int i = 1; i <= amount; i++) {
        for (int coin : coins) {
            if (coin <= i) {
                dp[i] = Math.min(dp[i], dp[i - coin] + 1);
            }
        }
    }

    return dp[amount] > amount ? -1 : dp[amount];
}

组合总和 Ⅳ（完全背包 - 排列）

输入：nums = [1,2,3], target = 4
输出：7
解释：
所有可能的组合为：
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意，顺序不同的序列被视作不同的组合。

image.png

public int combinationSum4(int[] nums, int target) {
    int len = nums.length;
    int[] dp = new int[target + 1];
    dp[0] = 1;
    for (int j = 1; j <= target; j++) {
        for (int num : nums) {
            if (j >= num) {
                dp[j] = dp[j] + dp[j-num];
            }
        }
    }

    return dp[target];
}