Ref:
- https://oi-wiki.org/math/quick-pow/
- https://zhuanlan.zhihu.com/p/95902286
矩阵快速幂
Ref: https://leetcode-cn.com/problems/climbing-stairs/solution/pa-lou-ti-by-leetcode-solution/
以上的方法适用于 n 比较小的情况,在 n 变大之后,O(n) 的时间复杂度会让这个算法看起来有些捉襟见肘。我们可以用「矩阵快速幂」的方法来优化这个过程。
首先我们可以构建这样一个递推关系: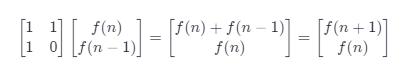
因此: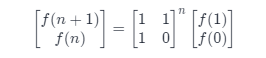
令: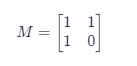
因此我们只要能快速计算矩阵 M 的 n 次幂,就可以得到 f(n) 的值。如果直接求取 M^n,时间复杂度是 O(n) 的,我们可以定义矩阵乘法,然后用快速幂算法来加速这里 M^n 的求取。
如何想到使用矩阵快速幂
- 如果一个问题可与转化为求解一个矩阵的 nn 次方的形式,那么可以用快速幂来加速计算
如果一个递归式形如
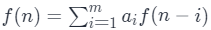 ,即齐次线性递推式,我们就可以把数列的递推关系转化为矩阵的递推关系,即构造出一个矩阵的 n 次方乘以一个列向量得到一个列向量,这个列向量中包含我们要求的 f(n)。一般情况下,形如
,即齐次线性递推式,我们就可以把数列的递推关系转化为矩阵的递推关系,即构造出一个矩阵的 n 次方乘以一个列向量得到一个列向量,这个列向量中包含我们要求的 f(n)。一般情况下,形如 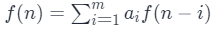 可以构造出这样的 m×m 的矩阵:
可以构造出这样的 m×m 的矩阵:那么遇到非齐次线性递推我们是不是就束手无策了呢?其实未必。有些时候我们可以把非齐次线性递推转化为其次线性递推,比如这样一个递推:

我们可以做这样的变换:
于是就可以使用矩阵快速幂求解了。并不是所有非齐次线性都可以化成齐次线性,我们还是要具体问题具体分析。
留两个思考题:
你能把 f(x) = 2f(x - 1) + 3f(x - 2) + 4cf(x)=2f(x−1)+3f(x−2)+4c 化成齐次线性递推吗?欢迎大家在评论区留言。
如果一个非齐次线性递推可以转化成齐次线性递推,那么一般方法是什么?这个问题也欢迎大家在评论区总结。
代码:
Java
public class Solution {public int climbStairs(int n) {int[][] q = {{1, 1}, {1, 0}};int[][] res = pow(q, n);return res[0][0];}public int[][] pow(int[][] a, int n) {int[][] ret = {{1, 0}, {0, 1}};while (n > 0) {if ((n & 1) == 1) {ret = multiply(ret, a);}n >>= 1;a = multiply(a, a);}return ret;}public int[][] multiply(int[][] a, int[][] b) {int[][] c = new int[2][2];for (int i = 0; i < 2; i++) {for (int j = 0; j < 2; j++) {c[i][j] = a[i][0] * b[0][j] + a[i][1] * b[1][j];}}return c;}}
Golang
type matrix [2][2]intfunc mul(a, b matrix) (c matrix) {for i := 0; i < 2; i++ {for j := 0; j < 2; j++ {c[i][j] = a[i][0]*b[0][j] + a[i][1]*b[1][j]}}return c}func pow(a matrix, n int) matrix {res := matrix{{1, 0}, {0, 1}}for ; n > 0; n >>= 1 {if n&1 == 1 {res = mul(res, a)}a = mul(a, a)}return res}func climbStairs(n int) int {res := pow(matrix{{1, 1}, {1, 0}}, n)return res[0][0]}
复杂度分析
时间复杂度:同快速幂,O(logn)。
空间复杂度:O(1)。

