Ref: https://pdai.tech/md/algorithm/alg-domain-bigdata-bloom-filter.html

0.相关题目

  1. 给你 A,B 两个文件，各存放 50 亿条 URL，每条 URL 占用 64 字节，内存限制是 4G，让你找出 A,B 文件共同的 URL。如果是三个乃至 n 个文件呢？

根据这个问题我们来计算下内存的占用，4G=2^32 大概是 40 亿 * 8 大概是 340 亿，n=50 亿，如果按出错率 0.01 算需要的大概是 650 亿个 bit。现在可用的是 340 亿，相差并不多，这样可能会使出错率上升些。另外如果这些 urlip 是一一对应的，就可以转换成 ip，则大大简单了。

  1. 给定 a、b 两个文件，各存放 50 亿个 url，每个 url 各占 64 字节，内存限制是 4G，让你找出 a、b 文件共同的 url?

如果允许有一定的错误率，可以使用 Bloom filter，4G 内存大概可以表示 340 亿 bit。将其中一个文件中的 url 使用 Bloom filter 映射为这 340 亿 bit，然后挨个读取另外一个文件的 url，检查是否与 Bloom filter，如果是，那么该 url 应该是共同的 url (注意会有一定的错误率)。”

  1. 在 2.5 亿个整数中找出不重复的整数，注，内存不足以容纳这 2.5 亿个整数。

方案1: 采用 2-Bitmap (每个数分配 2bit，00 表示不存在，01 表示出现一次，10 表示多次，11 无意义) 进行，共需内存 2^32 * 2 bit=1 GB 内存，还可以接受。然后扫描这 2.5 亿个整数，查看 Bitmap 中相对应位，如果是 00 变 01，01 变 10，10 保持不变。所描完事后，查看 bitmap，把对应位是 01 的整数输出即可。
方案2: 也可采用分治，划分小文件的方法。然后在小文件中找出不重复的整数，并排序。然后再进行归并，注意去除重复的元素。

  1. 给 40 亿个不重复的 unsigned int 的整数，没排过序的，然后再给一个数，如何快速判断这个数是否在那 40 亿个数当中？

用位图 / Bitmap 的方法，申请 512M 的内存，一个 bit 位代表一个 unsigned int 值。读入 40 亿个数，设置相应的 bit 位，读入要查询的数，查看相应 bit 位是否为 1，为 1 表示存在，为 0 表示不存在。

1.布隆过滤器由来

布隆在 1970 年提出了布隆过滤器 (Bloom Filter)，是一个很长的二进制向量 (可以想象成一个序列) 和一系列随机映射函数 (hash function)。可用于判断一个元素是否在一个集合中，查询效率很高 (1-N，最优能逼近于 1)。通常应用在一些需要快速判断某个元素是否属于集合，但是并不严格要求 100% 正确的场合。

特点

  • 优点: 占用空间小，查询快

  • 缺点: 有误判，删除困难

    几个专业术语

    这里有必要介绍一下 False Positive 和 False Negative 的概念:

  • False Positive: 中文可以理解为 “假阳性”，在这里表示，有可能把不属于这个集合的元素误认为属于这个集合

  • False Negative: 中文可以理解为 “假阴性”，Bloom Filter 是不存在 false negatived 的， 即不会把属于这个集合的元素误认为不属于这个集合 (False Negative)。

    2.布隆过滤器应用场景

  • 网页爬虫对URL的去重: 避免爬取相同的 URL 地址；

  • 反垃圾邮件: 假设邮件服务器通过发送方的邮件域或者 IP 地址对垃圾邮件进行过滤，那么就需要判断当前的邮件域或者 IP 地址是否处于黑名单之中。如果邮件服务器的通信邮件数量非常大 (也可以认为数据量级上亿)，那么也可以使用 Bloom Filter 算法；
  • 缓存击穿: 将已存在的缓存放到布隆中，当黑客访问不存在的缓存时迅速返回避免缓存及 DB 挂掉；
  • HTTP 缓存服务器: 当本地局域网中的 PC 发起一条 HTTP 请求时，缓存服务器会先查看一下这个 URL 是否已经存在于缓存之中，如果存在的话就没有必要去原始的服务器拉取数据了 (为了简单起见，我们假设数据没有发生变化)，这样既能节省流量，还能加快访问速度，以提高用户体验。
  • 黑/白名单: 类似反垃圾邮件。
  • Bigtable: Google 著名的分布式数据库 Bigtable 使用了布隆过滤器来查找不存在的行或列，以减少磁盘查找的 IO 次数。
  • Squid: 网页代理缓存服务器在 cachedigests 中使用了也布隆过滤器。
  • Venti 文档存储系统: 也采用布隆过滤器来检测先前存储的数据。
  • SPIN 模型检测器: 也使用布隆过滤器在大规模验证问题时跟踪可达状态空间。
  • Chrome 加速安全浏览: Google Chrome 浏览器使用了布隆过滤器加速安全浏览服务。
  • Key-Value 系统: 在很多 Key-Value 系统中也使用了布隆过滤器来加快查询过程，如 Hbase，Accumulo，Leveldb，一般而言，Value 保存在磁盘中，访问磁盘需要花费大量时间，然而使用布隆过滤器可以快速判断某个 Key 对应的 Value 是否存在，因此可以避免很多不必要的磁盘 IO 操作，只是引入布隆过滤器会带来一定的内存消耗。
  • HTTP Proxy-Cache: 在 Internet Cache Protocol 中的 Proxy-Cache 很多都是使用 Bloom Filter 存储 URLs，除了高效的查询外，还能很方便得传输交换 Cache 信息。

  • 网络应用: P2P 网络中查找资源操作，可以对每条网络通路保存 Bloom Filter，当命中时，则选择该通路访问。广播消息时，可以检测某个 IP 是否已发包。检测广播消息包的环路，将 Bloom Filter 保存在包里，每个节点将自己添加入 Bloom Filter。信息队列管理，使用 Counter Bloom Filter 管理信息流量。

    3.布隆过滤器实现

    Bloom Filter 在很多开源框架都有实现，例如:

  • Elasticsearch: org.elasticsearch.common.util.BloomFilter

  • guava: com.google.common.hash.BloomFilter
  • Hadoop: org.apache.hadoop.util.bloom.BloomFilter (基于 BitSet 实现)

    以 BitSet 实现方式为例

    创建一个 m 位 BitSet，先将所有位初始化为 0，然后选择 k 个不同的哈希函数。第 i 个哈希函数对字符串 str 哈希的结果记为 h(i, str)，且 h(i, str) 的范围是 0 到 m-1 。

    加入字符串过程

    下面是每个字符串处理的过程，首先是将字符串 str “记录” 到 BitSet 中的过程：对于字符串 str，分别计算 h(1, str)，h(2, str)…… h(k, str)。然后将 BitSet 的第 h(1, str)、h(2, str)…… h(k, str) 位设为 1。
    image.png
    这样就将字符串 str 映射到 BitSet 中的 k 个二进制位了。

    检查字符串是否存在的过程

    下面是检查字符串 str 是否被 BitSet 记录过的过程: 对于字符串 str，分别计算 h(1, str)，h(2, str)…… h(k, str)。然后检查 BitSet 的第 h(1, str)、h(2, str)…… h(k, str) 位是否为 1，若其中任何一位不为 1 则可以判定 str 一定没有被记录过。若全部位都是 1，则 “认为” 字符串 str 存在。 若一个字符串对应的 Bit 不全为 1，则可以肯定该字符串一定没有被 Bloom Filter 记录过。(这是显然的，因为字符串被记录过，其对应的二进制位肯定全部被设为 1 了)

    以 BitSet 实现代码

    ```java package algorithm; import java.util.BitSet;

public class BloomFilter {

  1. /* BitSet初始分配2^24个bit */
  2. private static final int DEFAULT_SIZE = 1 << 25;
  3. private BitSet bits = new BitSet(DEFAULT_SIZE);
  5. /* 不同哈希函数的种子，一般应取质数 */
  6. private static final int[] seeds = new int[]{ 5, 7, 11, 13, 31, 37, 61 };
  8. /* 哈希函数对象 */
  9. private SimpleHash[] func = new SimpleHash[seeds.length];
  11. public BloomFilter() {
  12.     for (int i = 0; i < seeds.length; i++) {
  13.         func[i] = new SimpleHash(DEFAULT_SIZE, seeds[i]);
  14.     }
  15. }
  17. // 将字符串标记到bits中
  18. public void add(String value) {
  19.     for (SimpleHash f : func) {
  20.         bits.set(f.hash(value), true);
  21.     }
  22. }
  24. // 判断字符串是否已经被bits标记
  25. public boolean contains(String value) {
  26.     if (value == null) {
  27.         return false;
  28.     }
  29.     boolean ret = true;
  30.     for (SimpleHash f : func) {
  31.         ret = ret && bits.get(f.hash(value));
  32.     }
  33.     return ret;
  34. }
  36. /* 哈希函数类 */
  37. public static class SimpleHash {
  38.     private int cap;
  39.     private int seed;
  41.     public SimpleHash(int cap, int seed) {
  42.         this.cap = cap;
  43.         this.seed = seed;
  44.     }
  46.     // hash函数，采用简单的加权和hash
  47.     public int hash(String value) {
  48.         int result = 0;
  49.         int len = value.length();
  50.         for (int i = 0; i < len; i++) {
  51.             result = seed * result + value.charAt(i);
  52.         }
  53.         return (cap - 1) & result;
  54.     }
  55. }

} ```

4.误报率 - False Positive Rate

误报率的产生

初始状态下，Bloom Filter 是一个 m 位的位数组，且数组被 0 所填充。同时，我们需要定义 k 个不同的 hash 函数，每一个 hash 函数都随机的将每一个输入元素映射到位数组中的一个位上。那么对于一个确定的输入，我们会得到 k 个索引。
插入元素：经过 k 个 hash 函数的映射，我们会得到 k 个索引，我们把位数组中这 k 个位置全部置 1 (不管其中的位之前是 0 还是 1)
查询元素：输入元素经过 k 个 hash 函数的映射会得到 k 个索引，如果位数组中这 k 个索引任意一处是 0，那么就说明这个元素不在集合之中；如果元素处于集合之中，那么当插入元素的时候这 k 个位都是 1。但如果这 k 个索引处的位都是 1，被查询的元素就一定在集合之中吗？答案是不一定，也就是说出现了 False Positive 的情况 (但 Bloom Filter 不会出现 False Negative 的情况)
image.png
在上图中，当插入 x、y、z 这三个元素之后，再来查询 w，会发现 w 不在集合之中，而如果 w 经过三个 hash 函数计算得出的结果所得索引处的位全是 1，那么 Bloom Filter 就会告诉你，w 在集合之中，实际上这里是误报，w 并不在集合之中。

误报率的计算

Bloom Filter 的误报率到底有多大？下面在数学上进行一番推敲。假设 HASH 函数输出的索引值落在 m 位的数组上的每一位上都是等可能的。那么，对于一个给定的 HASH 函数，在进行某一个运算的时候，一个特定的位没有被设置为 1 的概率是
image.png
那么，对于所有的 k 个 HASH 函数，都没有把这个位设置为 1 的概率是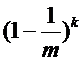
image.png
如果我们已经插入了 n 个元素，那么对于一个给定的位，这个位仍然是 0 的概率是
image.png
那么，如果插入 n 个元素之后，这个位是 1 的概率是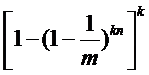
image.png
如果对一个特定的元素存在误报，那么这个元素的经过 HASH 函数所得到的 k 个索引全部都是 1，概率也就是
image.png
根据常数 e 的定义，可以近似的表示为: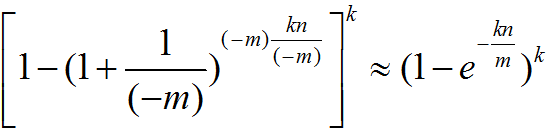
image.png

减少误报率：最优的哈希函数个数

既然 Bloom Filter 要靠多个哈希函数将集合映射到位数组中，那么应该选择几个哈希函数才能使元素查询时的错误率降到最低呢？这里有两个互斥的理由：

  • 如果哈希函数的个数多，那么在对一个不属于集合的元素进行查询时得到 0 的概率就大；
  • 但另一方面，如果哈希函数的个数少，那么位数组中的 0 就多。

为了得到最优的哈希函数个数，我们需要根据上一小节中的错误率公式进行计算。

先用 p 和 f 进行计算。注意到 f = exp (k ln (1 − e−kn/m))，我们令 g = k ln (1 − e−kn/m)，只要让 g 取到最小，f 自然也取到最小。由于 p = e-kn/m，我们可以将 g 写成
image.png
根据对称性法则可以很容易看出当 p = 1/2，也就是 k = ln2・(m/n) 时，g 取得最小值。在这种情况下，最小错误率 f 等于 (1/2) k ≈ (0.6185) m/n。另外，注意到 p 是位数组中某一位仍是 0 的概率，所以 p = 1/2 对应着位数组中 0 和 1 各一半。换句话说，要想保持错误率低，最好让位数组有一半还空着。
需要强调的一点是，p = 1/2 时错误率最小这个结果并不依赖于近似值 p 和 f。同样对于 f’ = exp (k ln (1 − (1 − 1/m) kn))，g’ = k ln (1 − (1 − 1/m) kn)，p’ = (1 − 1/m) kn，我们可以将 g’写成
image.png
同样根据对称性法则可以得到当 p’ = 1/2 时，g’取得最小值。

减少误报率：位数组的大小

在不超过一定错误率的情况下，Bloom Filter 至少需要多少位才能表示全集中任意 n 个元素的集合？假设全集中共有 u 个元素，允许的最大错误率为є，下面我们来求位数组的位数 m。
假设 X 为全集中任取 n 个元素的集合，F (X) 是表示 X 的位数组。那么对于集合 X 中任意一个元素 x，在 s = F (X) 中查询 x 都能得到肯定的结果，即 s 能够接受 x。显然，由于 Bloom Filter 引入了错误，s 能够接受的不仅仅是 X 中的元素，它还能够є (u - n) 个 false positive。因此，对于一个确定的位数组来说，它能够接受总共 n + є (u - n) 个元素。在 n + є (u - n) 个元素中，s 真正表示的只有其中 n 个，所以一个确定的位数组可以表示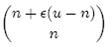
image.png
个集合。m 位的位数组共有 2m 个不同的组合，进而可以推出，m 位的位数组可以表示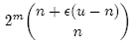
image.png
个集合。全集中 n 个元素的集合总共有
image.png
个，因此要让 m 位的位数组能够表示所有 n 个元素的集合，必须有
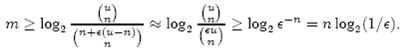
image.png
即:
image.png
上式中的近似前提是 n 和єu 相比很小，这也是实际情况中常常发生的。根据上式，我们得出结论：在错误率不大于є的情况下，m 至少要等于 n log2 (1/є) 才能表示任意 n 个元素的集合。
上一小节中我们曾算出当 k = ln2・(m/n) 时错误率 f 最小，这时 f = (1/2) k = (1/2) mln2 /n。现在令 f≤є，可以推出
image.png
这个结果比前面我们算得的下界 n log2 (1/є) 大了 log2 e ≈ 1.44 倍。这说明在哈希函数的个数取到最优时，要让错误率不超过є，m 至少需要取到最小值的 1.44 倍。

5.拓展: Counting Bloom Filter

从前面对 Bloom Filter 的介绍可以看出，标准的 Bloom Filter 是一种很简单的数据结构，它只支持插入和查找两种操作。在所要表达的集合是静态集合的时候，标准 Bloom Filter 可以很好地工作，但是如果要表达的集合经常变动，标准 Bloom Filter 的弊端就显现出来了，因为它不支持删除操作。

Counting Bloom Filter 的出现解决了这个问题，它将标准 Bloom Filter 位数组的每一位扩展为一个小的计数器 (Counter)，在插入元素时给对应的 k (k 为哈希函数个数) 个 Counter 的值分别加 1，删除元素时给对应的 k 个 Counter 的值分别减 1。Counting Bloom Filter 通过多占用几倍的存储空间的代价，给 Bloom Filter 增加了删除操作。下一个问题自然就是，到底要多占用几倍呢？
image.png
我们先计算第 i 个 Counter 被增加 j 次的概率，其中 n 为集合元素个数，k 为哈希函数个数，m 为 Counter 个数 (对应着原来位数组的大小):
image.png
上面等式右端的表达式中，前一部分表示从 nk 次哈希中选择 j 次，中间部分表示 j 次哈希都选中了第 i 个 Counter，后一部分表示其它 nk – j 次哈希都没有选中第 i 个 Counter。因此，第 i 个 Counter 的值大于 j 的概率可以限定为: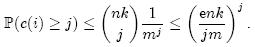
image.png
上式第二步缩放中应用了估计阶乘的斯特林公式:
image.png
在 Bloom Filter 概念和原理一文中，我们提到过 k 的最优值为 (ln2) m/n，现在我们限制 k ≤ (ln2) m/n，就可以得到如下结论:
image.png
如果每个 Counter 分配 4 位，那么当 Counter 的值达到 16 时就会溢出。这个概率为: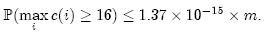
image.png
这个值足够小，因此对于大多数应用程序来说，4 位就足够了。

6.拓展：其它

  • Data synchronization：Byers 等人提出了使用布隆过滤器近似数据同步。
  • Bloomier filters：Chazelle 等人提出了一个通用的布隆过滤器，该布隆过滤器可以将某一值与每个已经插入的元素关联起来，并实现了一个关联数组 Map。与普通的布隆过滤器一样，Chazelle 实现的布隆过滤器也可以达到较低的空间消耗，但同时也会产生 false positive，不过，在 Bloomier filter 中，某 key 如果不在 map 中，false positive 在会返回时会被定义出的。该 Map 结构不会返回与 key 相关的在 map 中的错误的值。
  • Compact approximators
  • Stable Bloom filters
  • Scalable Bloom filters
  • Attenuated Bloom filters