一、二叉树入门

之前我们实现的符号表中，不难看出，符号表的增删查操作，随着元素个数N的增多，其耗时也是线性增多的，时 间复杂度都是O(n),为了提高运算效率，接下来我们学习树这种数据结构。

1.1 树的基本定义

树是我们计算机中非常重要的一种数据结构，同时使用树这种数据结构，可以描述现实生活中的很多事物，例如家谱、单位的组织架构、等等。
树是由n(n>=1)个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就 是说它是根朝上，而叶朝下的。
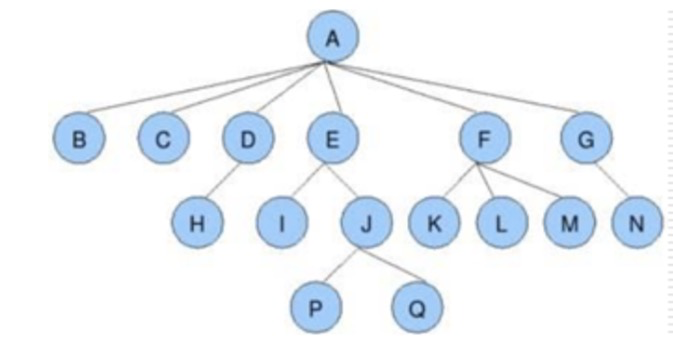
image.png
树具有以下特点:

  1. 每个结点有零个或多个子结点;
  2. 没有父结点的结点为根结点;
  3. 每一个非根结点只有一个父结点;

  4. 每个结点及其后代结点整体上可以看做是一棵树，称为当前结点的父结点的一个子树;

    1.2 树的相关术语

    结点的度:
    一个结点含有的子树的个数称为该结点的度;
    叶结点:
    度为0的结点称为叶结点，也可以叫做终端结点
    分支结点:
    度不为0的结点称为分支结点，也可以叫做非终端结点
    结点的层次:
    从根结点开始，根结点的层次为1，根的直接后继层次为2，以此类推
    结点的层序编号:
    将树中的结点，按照从上层到下层，同层从左到右的次序排成一个线性序列，把他们编成连续的自然数。
    树的度:
    树中所有结点的度的最大值
    树的高度(深度):
    树中结点的最大层次
    森林:
    m(m>=0)个互不相交的树的集合，将一颗非空树的根结点删去，树就变成一个森林;给森林增加一个统一的根 结点，森林就变成一棵树
    孩子结点:
    一个结点的直接后继结点称为该结点的孩子结点
    双亲结点(父结点):
    一个结点的直接前驱称为该结点的双亲结点
    兄弟结点:
    同一双亲结点的孩子结点间互称兄弟结点

    1.3 二叉树的基本定义

    二叉树就是度不超过2的树(每个结点最多有两个子结点)
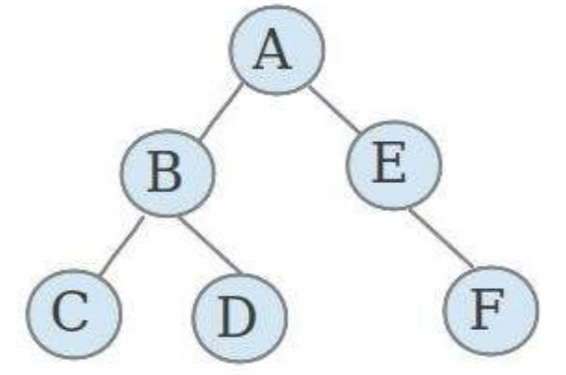
    image.png
    满二叉树:
    一个二叉树，如果每一个层的结点树都达到最大值，则这个二叉树就是满二叉树。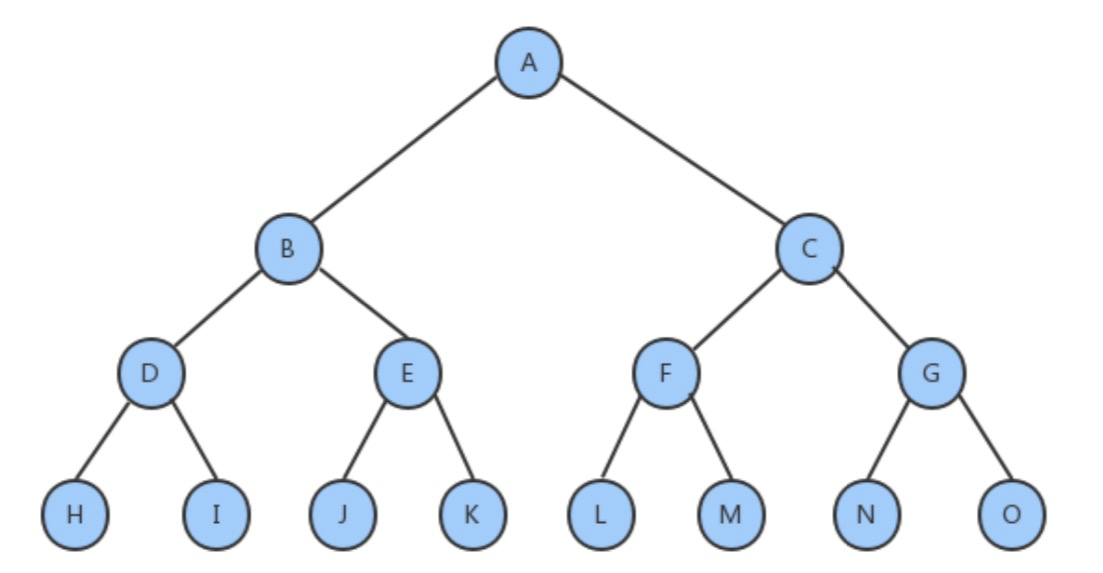
    image.png
    完全二叉树:
    叶节点只能出现在最下层和次下层，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树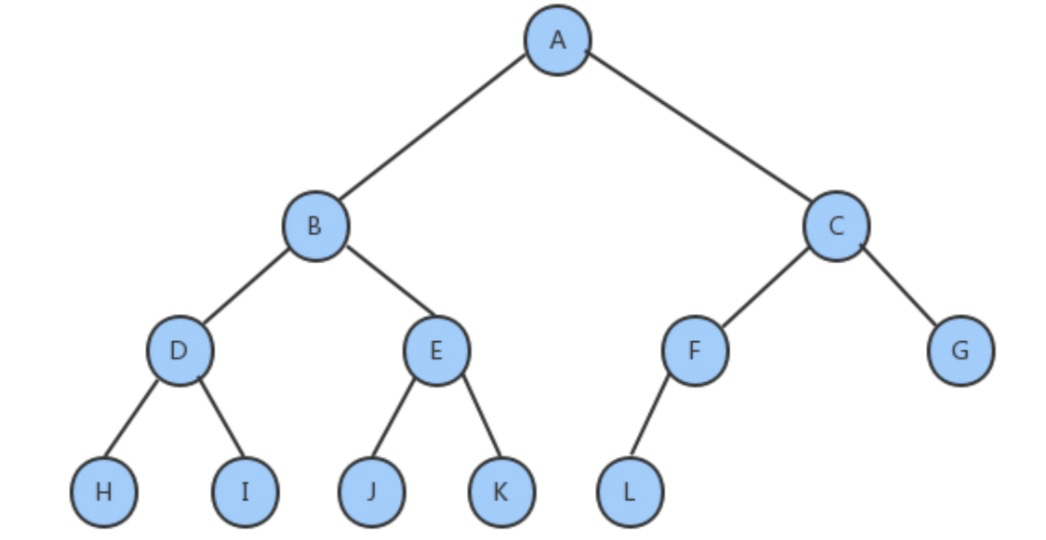
    image.png

    1.4 二叉查找树的创建

    1.4.1二叉树的结点类

    根据对图的观察，我们发现二叉树其实就是由一个一个的结点及其之间的关系组成的，按照面向对象的思想，我们设计一个结点类来描述结点这个事物。
    结点类API设计: 

    1.          |                     **类名**                                                                         | **Node<Key,Value>**                                                                                         |

    | —- | —- | | 构造方法 | Node(Key key, Value value, Node left, Node right):创建Node对象 | | 成员变量 | 1.public Node left:记录左子结点
    2.public Node right:记录右子结点
    3.public Key key:存储键
    4.public Value value:存储值 |

    1.  <br />    <br />[06_树的入门.pdf](https://www.yuque.com/attachments/yuque/0/2021/pdf/384158/1610332615080-d038e017-2055-4d7e-b516-be72173aa8e4.pdf)<br />                                                            <br />                                                            <br />                                                            <br />                                                            <br />                                                            <br />                                                            <br />                                                            <br />                                                            <br />                                                            <br />                                                            <br />                                                            <br />                                                            <br />                                                                                                                <br />