Task01 Data类与Dataset类

1. PyG中图的表示及使用——Data类

1.1 Data对象的创建

1.1.1 通过构造函数

Data类的构造函数如下，

class Data(object):
    def __init__(self, x=None, edge_index=None, edge_attr=None, y=None, **kwargs):
    r"""
    Args:
        x (Tensor, optional): 节点属性矩阵，大小为`[num_nodes, num_node_features]`
        edge_index (LongTensor, optional): 边索引矩阵，大小为`[2, num_edges]`，第0行为尾节点，第1行为头节点，头指向尾
        edge_attr (Tensor, optional): 边属性矩阵，大小为`[num_edges, num_edge_features]`
        y (Tensor, optional): 节点、图或者是边的标签，任意大小
    """
    self.x = x
    self.edge_index = edge_index
    self.edge_attr = edge_attr
    self.y = y
    for key, item in kwargs.items():
        if key == 'num_nodes':
            self.__num_nodes__ = item
        else:
            self[key] = item

• edge_index的每一列定义一条边，其中第一行为边起始节点的索引，第二行为边结束节点的索引。这种表示方法被称为COO格式（coordinate format），通常用于表示稀疏矩阵。
• PyG不是用稠密矩阵来持有邻接矩阵的信息，而是用仅存储邻接矩阵中非元素的稀疏矩阵来表示图。
• 通常，一个图至少包含x, edge_index, edge_attr, y, num_nodes5个属性，当图包含其他属性时，我们可以通过指定额外的参数使**Data**对象包含其他的属性：

  graph = Data(x=x, edge_index=edge_index, edge_attr=edge_attr, y=y, num_nodes=num_nodes, other_attr=other_attr)

下面来看一个示例

import torch
from torch_geometric.data import Data
edge_index = torch.tensor([[0, 1, 1, 2],
                           [1, 0, 2, 1]], dtype=torch.long)
x = torch.tensor([[-1], 
                  [0], 
                  [1]], dtype=torch.float)
data = Data(x=x, edge_index=edge_index)
# Data(edge_index=[2, 4], x=[3, 1])

上面这段代码产生的图的结构如下图所示

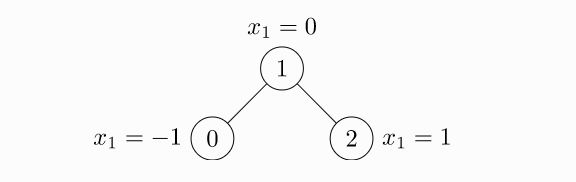
如果要用edge_index定义节点索引元组列表的话，应该使用contigious在将他们传递给构造函数前先进行转置操作，再调用该方法，代码如下：

from torch_geometric.data import Data
edge_index = torch.tensor([[0, 1],
                           [1, 0],
                           [1, 2],
                           [2, 1]], dtype=torch.long)
x = torch.tensor([[-1], [0], [1]], dtype=torch.float)
data = Data(x=x, edge_index=edge_index.t().contiguous())
# Data(edge_index=[2, 4], x=[3, 1])

这里每一条边用两个元组定义，说明每条边的两个方向。

1.1.2 将dict对象转为Data对象

也可以将一个dict对象转边为一个Data对象，代码如下：

graph_dict = {
    'x': x,
    'edge_index': edge_index,
    'edge_attr': edge_attr,
    'y': y,
    'num_nodes': num_nodes,
    'other_attr': other_attr
}
graph_data = Data.from_dict(graph_dict)

这里from_dict是一个类方法：

@classmethod
def from_dict(cls, dictionary):
    r"""Creates a data object from a python dictionary."""
    data = cls()
    for key, item in dictionary.items():
        data[key] = item
    return data

【注意】：graph_dict中属性值的类型与大小的要求与Data类的构造函数的要求相同。

1.2 Data对象的常见操作

Data类由许多实用函数对实例对象操作，下面来简单看一下这些操作

# 获取Data对象包含的属性的关键字
print(data.keys)
# ['x', 'edge_index']
# 获取属性
print(data['x'])
# tensor([[-1.0], [0.0], [1.0]])
# 设置属性
data['x'] = x
for key, item in data:
    print("{} found in data".format(key))
# x found in data
# edge_index found in data
'edge_attr' in data
# False
# 对边排序并移除重复的边
graph_data.coalesce()
# 节点数量
data.num_nodes
# 3
# 边数量
data.num_edges
# 4
# 节点属性的维度，边属性的维度查找同理
# data.node_features
data.num_node_features
# 1
# 是否含有孤立节点
data.contains_isolated_nodes()
# False
# 是否含有自环边
data.contains_self_loops()
# False
# 是否为有向图
data.is_directed()
# False
# 用作训练集的节点
data.train_mask.sum()
# 用作训练集的节点的数量
int(data.train_mask.sum()) / data.num_nodes
# Transfer data object to GPU.
device = torch.device('cuda')
data = data.to(device)

1.3 Data对象转变为其他的数据

• Data对象转换为dict对象：

  def to_dict(self):
   return {key: item for key, item in self}

• Data对象转换为namedtuple：

  def to_namedtuple(self):
   keys = self.keys
   DataTuple = collections.namedtuple('DataTuple', keys)
   return DataTuple(*[self[key] for key in keys])

2. PyG中图数据集的表示及使用——Dataset类

PyG内置了大量常用的基准数据集，接下来以PyG内置的Planetoid数据集为例，来学习PyG中图数据集的表示及使用。

2.1 生成数据集对象并分析数据集

在第一次生成PyG内置的数据集时，程序首先下载原始文件，然后将原始文件处理成包含**Data**对象的**Dataset**对象并保存到文件。代码如下：

from torch_geometric.datasets import Planetoid
dataset = Planetoid(root='/dataset/Cora', name='Cora')
# Cora()
len(dataset)
# 1
dataset.num_classes
# 7
dataset.num_node_features
# 1433

2.2 分析数据集中样本

从上一节中可以看出，该数据集只有一个图，包含7个分类，节点的属性为1433维。

data = dataset[0]
# Data(edge_index=[2, 10556], test_mask=[2708],
#         train_mask=[2708], val_mask=[2708], x=[2708, 1433], y=[2708])
data.is_undirected()
# True
data.train_mask.sum().item()
# 140
data.val_mask.sum().item()
# 500
data.test_mask.sum().item()
# 1000

该数据集包含唯一一个图，有2708个节点，节点特征为1433维，有10556条边，有140个用作训练集的节点，有500个用作验证集的节点，有1000个用作测试集的节点。

2.3 自定义切分数据集

以 ENZYMES 数据集（含有6个分类，600张图）为例

from torch_geometric.datasets import TUDataset
dataset = TUDataset(root='/tmp/ENZYMES', name='ENZYMES')
# 访问第一个图
data = dataset[0]
print(data)
# Data(edge_index=[2, 168], x=[37, 3], y=[1])
# 使用切片分割数据集，要求训练集和测试集的比例是7：3
train_data = dataset[:420]
test_data = dataset[420:]
print(train_data, ',', test_data)
# ENZYMES(420), ENZYMES(180)
# 如果不确定在拆分之前数据集是否已经打乱，可以通过运行如下函数来随机排列数据集
dataset = dataset.shuffle()

2.4 数据集的使用

假设已经定义好了一个图神经网络模型，其名为Net。在下方的代码中，展示了节点分类图数据集在训练过程中的使用。

devic = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Net().to(device)
data = dataset[0].to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)
model.train()
for epoch in range(200):
    optimizer.zero_grad()
    out = model(data)
    loss = F.nll_loss(out[data.train_mask], data.y[data.train_mask])
    loss.backward()
    optimizer.step()

3. 小批量处理

神经网络通常以批处理方式进行训练。PyG通过创建稀疏块对角邻接矩阵（由edge_index定义）并在节点维度中连接特征和目标矩阵来实现小批量的并行化。这种组合允许在一批中的示例上有不同数量的节点和边，如下图所示

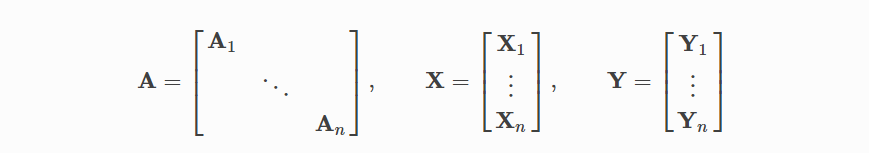
PyG中包含其自身的torch_geometric.data.DataLoader,其可以处理这一连接过程，下面来看一个例子

from torch_geometric.datasets import TUDataset
from torch_geometric.data import DataLoader
dataset = TUDataset(root='/Dataset/ENZYMES', name='ENZYMES', use_node_attr=True)
loader = DataLoader(dataset, batch_size=32, shuffle=True)
for batch in loader:
    print(batch)
    print(batch.num_graphs)

结果如下图所示

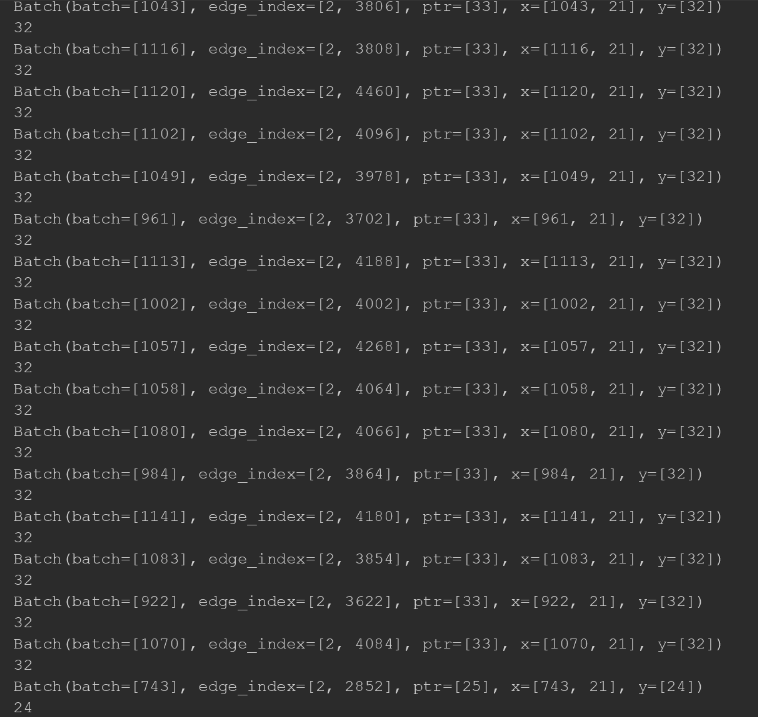
torch_geometric.data.Batch继承torch_geometric.data.Data，并包含一个batch附加属性

batch是一个列向量，它在批处理中将每个节点映射到其各自的图：

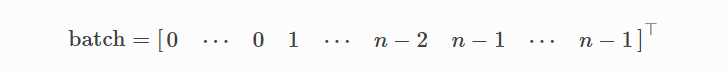
可以利用它来对每个图在节点维度上平均节点特征

from torch_scatter import scatter_mean
from torch_geometric.datasets import TUDataset
from torch_geometric.data import DataLoader
dataset = TUDataset(root='/tmp/ENZYMES', name='ENZYMES', use_node_attr=True)
loader = DataLoader(dataset, batch_size=32, shuffle=True)
for data in loader:
    x = scatter_mean(data.x, data.batch, dim=0)
    print(x.size())

结果如下图所示：

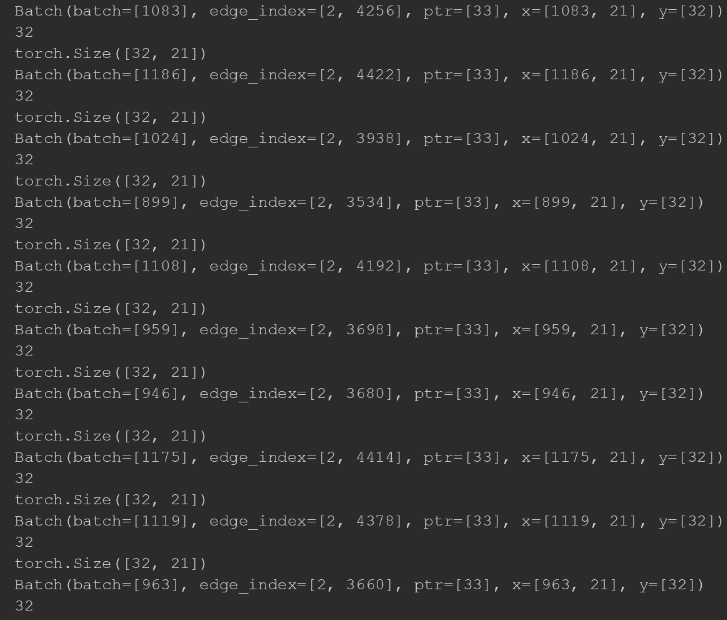
4. 数据转换

转换是torchvision变换图像和执行增强的常用方法。PyG带有自己的转换，它以一个Data对象作为输入并返回一个新的变换后的Data对象。可以使用torch_geometric.transforms.Compose在将处理过的数据集保存到磁盘 (pre_transform) 或访问数据集中的图形(transform)之前将转换链接在一起。

下面来看一个例子，在ShapEnet数据集上使用转换（包含17000个3D形状点云和16个形状类别的标签）

from torch_geometric.datasets import ShapeNet
dataset = ShapeNet(root='/tmp/ShapeNet', categories=['Airplane'])
print(dataset[0])
# Data(pos=[2518, 3], y=[2518])

我们可以通过转换从点云生成最近邻图来将点云数据集转换为图数据集（简单来说，就是通过KNN算法寻找节点的邻居，然后加边生成图）

import torch_geometric.transforms as T
from torch_geometric.datasets import ShapeNet
dataset = ShapeNet(root='/tmp/ShapeNet', categories=['Airplane'],
                    pre_transform=T.KNNGraph(k=6))
print(dataset[0])
# Data(edge_index=[2, 15108], pos=[2518, 3], y=[2518])

【注意】：使用pre_transform将数据保存至磁盘后，下一次启动时它已经包含图形的边，即使未通过任何转换。

此外，我们可以使用transform参数随机增强对象，比如，将每个节点位置平移一个小数

import torch_geometric.transforms as T
from torch_geometric.datasets import ShapeNet
dataset = ShapeNet(root='/tmp/ShapeNet', categories=['Airplane'],
                    pre_transform=T.KNNGraph(k=6),
                    transform=T.RandomTranslate(0.01))
print(dataset[0])
# Data(edge_index=[2, 15108], pos=[2518, 3], y=[2518])

5. 作业

要求：请通过继承Data类实现一个类，专门用于表示“机构-作者-论文”的网络。该网络包含“机构“、”作者“和”论文”三类节点，以及“作者-机构“和“作者-论文“两类边。对要实现的类的要求：

1）用不同的属性存储不同节点的属性；

2）用不同的属性存储不同的边（边没有属性）；

3）逐一实现获取不同节点数量的方法。

分析：

• 节点有三类，分别记为 P：论文；A：作者；I：机构
• 边有两类，分别记为 AtoI：作者-机构；AtoP：作者-论文
• 这里可以视为两个二分图（作者-机构图和作者-论文图）存放在一个Data对象中
• 代码参考了PyG实现将两个图（源图：和目标图）存储在一个Data中的代码以及PyG实现二分图的代码和社区的标准答案来实现

代码：

    def __init__(self, x_p, x_a, x_i, edge_index_a2p, edge_index_a2i, edge_attr_a2p=None, edge_attr_a2i=None):
        super(myData, self).__init__()
        self.edge_index_a2p = edge_index_a2p
        self.edge_attr_a2p = edge_attr_a2p
        self.edge_index_a2i = edge_index_a2i
        self.edge_attr_a2i = edge_attr_a2i
        self.x_p = x_p
        self.x_a = x_a
        self.x_i = x_i

在这种定义下，edge_index_a2p、edge_index_a2i应该相对独立的增加边对应的源节点和目标节点，比如 edge_index_a2p应该增加[[self.x_a.size(0)], [self.x_i.size(0)]]

    def __inc__(self, key, value):
        if key == 'edge_index_a2p':
            return torch.tensor([[self.x_a.size(0)], [self.x_p.size(0)]])
        if key == 'edge_index_a2i':
            return torch.tensor([[self.x_a.size(0)], [self.x_i.size(0)]])
        else:
            return super().__inc__(key, value)

实现取不同属性的节点的数量的方法：

    @property
    def num_paper_Nodes(self):
        return self.x_p.shape[0]
    @property
    def num_author_Nodes(self):
        return self.x_a.shape[0]
    @property
    def num_institution_Nodes(self):
        return self.x_i.shape[0]

测试代码：

# 测试部分 假设作者数：3 论文数：2 机构数：2
x_a = torch.randn(3,4)
x_p = torch.randn(2,6)
x_i = torch.randn(2,3)
edge_index_a2p = torch.tensor([[0, 1, 1, 2],
                               [0, 0, 1, 1]], dtype=torch.long)
edge_index_a2i = torch.tensor([[0,1,2],
                               [0,0,1]], dtype=torch.long)
data = myData(x_a=x_a, x_p=x_p, x_i=x_i, edge_index_a2p=edge_index_a2p, edge_index_a2i=edge_index_a2i)
data
'''
    myData(edge_index_a2i=[2, 3], edge_index_a2p=[2, 4], x_a=[3, 4], x_i=[2, 3], x_p=[2, 6])
'''
data.num_author_Nodes
# 3

6. 参考资料

• DataWhale开源学习资料：https://github.com/datawhalechina/team-learning-nlp/tree/master/GNN
• PyG官方文档：https://pytorch-geometric.readthedocs.io/en/latest/index.html