1. 消息传播
1.1 简介
消息传播范式是一种聚合邻接节点信息来更新中心节点信息的范式,它将卷积算子推广到了不规则数据领域,实现了图与神经网络的连接。此范式包含三个步骤:
1)邻接节点信息变换
2)邻接节点信息聚合到中心节点
3)聚合信息变换
1.2 原理
用%7Di%5Cin%5Cmathbb%7BR%7D%5EF#card=math&code=%5Cmathbf%7Bx%7D%5E%7B%28k-1%29%7D_i%5Cin%5Cmathbb%7BR%7D%5EF&id=vLCXI)表示
#card=math&code=%28k-1%29&id=uj6kG)层中节点
的节点特征, 表示从节点
到节点
的边的特征,消息传递图神经网络可以描述为
%7D%20%3D%20%5Cgamma%5E%7B(k)%7D%20%5Cleft(%20%5Cmathbf%7Bx%7Di%5E%7B(k-1)%7D%2C%20%5Csquare%7Bj%20%5Cin%20%5Cmathcal%7BN%7D(i)%7D%20%5C%2C%20%5Cphi%5E%7B(k)%7D%5Cleft(%5Cmathbf%7Bx%7Di%5E%7B(k-1)%7D%2C%20%5Cmathbf%7Bx%7D_j%5E%7B(k-1)%7D%2C%5Cmathbf%7Be%7D%7Bj%2Ci%7D%5Cright)%20%5Cright)%2C%0A#card=math&code=%5Cmathbf%7Bx%7Di%5E%7B%28k%29%7D%20%3D%20%5Cgamma%5E%7B%28k%29%7D%20%5Cleft%28%20%5Cmathbf%7Bx%7D_i%5E%7B%28k-1%29%7D%2C%20%5Csquare%7Bj%20%5Cin%20%5Cmathcal%7BN%7D%28i%29%7D%20%5C%2C%20%5Cphi%5E%7B%28k%29%7D%5Cleft%28%5Cmathbf%7Bx%7Di%5E%7B%28k-1%29%7D%2C%20%5Cmathbf%7Bx%7D_j%5E%7B%28k-1%29%7D%2C%5Cmathbf%7Be%7D%7Bj%2Ci%7D%5Cright%29%20%5Cright%29%2C%0A&id=T4rmR)
其中表示可微分的、具有排列不变性(函数输出结果与输入参数的排列无关)的函数。具有排列不变性的函数有
**Sum**函数、**Mean**函数和**Max**函数。和
表示可微分的函数,如MLPs(多层感知器)。
对公式的理解:
%7D(xi%5E%7B(k-1)%7D%2C%20x_j%5E%7B(k-1)%7D%2Ce%7Bj%2Ci%7D)#card=math&code=%5Cphi%5E%7B%28k%29%7D%28xi%5E%7B%28k-1%29%7D%2C%20x_j%5E%7B%28k-1%29%7D%2Ce%7Bj%2Ci%7D%29&id=WPCD9)表示邻节点的信息聚合
%7D#card=math&code=%5Csquare_%7Bj%20%5Cin%20%5Cmathcal%7BN%7D%28i%29%7D&id=Cw8TV)表示池化方式
下方图片展示了基于消息传递范式的聚合邻接节点信息来更新中心节点信息的过程:
- 在图中黄色方框部分,B节点的邻接节点(A, C)的信息经过变换后聚合到B节点,接着B节点信息与邻接节点聚合信息一起经过变换得到B节点的新的节点信息。同时,分别如红色和绿色方框部分所示,C、D节点也遵循同样的过程更新信息。这种过程会在所有节点上都进行一遍,即所有节点的信息都会更新。
- 这样的“邻接节点信息传递到中心节点的过程”会进行多次。如图中蓝色方框部分所示,A节点的邻接节点(B,C,D)的已经发生过一次更新的节点信息,经过变换、聚合、再变换产生了A节点第二次更新的节点信息。多次更新后的节点信息就作为节点表征。

2. PyG实现消息传播网络
2.1 一个简单的图神经网络实例
本节将使用一个简单的GCN在Cora引文数据集上进行实验。代码如下
import torchimport torch.nn.functional as Ffrom torch_geometric.datasets import Planetoidfrom torch_geometric.nn import GCNConv# 加载数据集dataset = Planetoid(root='/Datasets/Cora', name='Cora')# 实现一个两层的GCNclass Net(torch.nn.Module):def __init__(self):super(Net, self).__init__()self.conv1 = GCNConv(dataset.num_node_features, 16)self.conv2 = GCNConv(16, dataset.num_classes)def forward(self, data):x, edge_index = data.x, data.edge_indexx = self.conv1(x, edge_index)x = F.relu(x)x = F.dropout(x, training=self.training)x = self.conv2(x, edge_index)return F.log_softmax(x, dim=1)# 定义模型device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')model = Net().to(device)data = dataset[0].to(device)optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)# 训练部分model.train()for epoch in range(200):optimizer.zero_grad()out = model(data)loss = F.nll_loss(out[data.train_mask], data.y[data.train_mask])loss.backward()optimizer.step()# 在测试节点上评估模型model.eval()_, pred = model(data).max(dim=1)correct = int(pred[data.test_mask].eq(data.y[data.test_mask]).sum().item())acc = correct / int(data.test_mask.sum())print('Accuracy:{:.4f}'.format(acc))
结果:

2.2 PyG中的MessagePassing基类
Pytorch Geometric提供了MessagePassing基类,它实现了消息传播的自动处理,继承该基类可使我们方便地构造消息传播图神经网络,我们只需定义函数,即
**message()**方法,和函数,即
**update()**方法,以及使用的消息聚合方式,即**aggr="add"**、**aggr="mean"**或**aggr="max"**。这些是在以下方法的帮助下完成的:
MessagePassing(aggr="add", flow="source_to_target", node_dim=-2):aggr:定义要使用的聚合方案(”add”、”mean “或 “max”);flow:定义消息传递的流向(”source_to_target “或 “target_to_source”);**node_dim**:定义沿着哪个轴线传播。
MessagePassing.propagate(edge_index, size=None, **kwargs):- 开始传播消息的起始调用,在此方法中
**message**、**update**等方法被调用。 - 它以
edge_index(边的端点的索引)和flow(消息的流向)以及一些额外的数据为参数,参数说明如下:**edge_index**: 边端点索引,它可以是**Tensor**类型或**SparseTensor**类型。- 当flow=”source_to_target”时,节点
**edge_index[0]**的信息将被传递到节点**edge_index[1]** - 当flow=”target_to_source”时,节点
**edge_index[1]**的信息将被传递到节点**edge_index[0]**
- 当flow=”source_to_target”时,节点
- 开始传播消息的起始调用,在此方法中
(这也说明了**edge_index[0]**表示源节点列表,**edge_index[1]**表示目标节点列表)
- `size`: 邻接节点的数量与中心节点的数量。- 对于普通图,邻接节点的数量与中心节点的数量都是N,我们可以不给size传参数,即`size=None`,这时假定矩阵是对称的。- `propagate()`不仅限于在形状为`[N, N]`的对称邻接矩阵中交换消息,还可以**通过传递**`**size=(N, M)**`**作为额外参数。例如,在二部图的形状为**`**[N, M]**`**的一般稀疏分配矩阵中交换消息**。- 对于**有两个独立的节点集合和索引集合的二分图,并且每个集合都持有自己的信息,我们可以传递一个元组参数,即**`**x=(x_N, x_M)**`**,来标记信息的区分。**- `kwargs`: 图其他属性或额外的数据。
edge_index是propagate函数必须的参数。在**message**函数中希望接受到哪些数据(或图的属性或额外的数据),就要在**propagate**函数的调用中传递哪些参数。
[MessagePassing.message(...)](https://pytorch-geometric.readthedocs.io/en/latest/modules/nn.html#torch_geometric.nn.conv.message_passing.MessagePassing.message):- 首先确定要给节点
传递消息的边的集合,如果
flow="source_to_target",则是%20%5Cin%20%5Cmathcal%7BE%7D#card=math&code=%28j%2Ci%29%20%5Cin%20%5Cmathcal%7BE%7D&id=PaZA3)的边的集合;
- 如果
flow="target_to_source",则是%20%5Cin%20%5Cmathcal%7BE%7D#card=math&code=%28i%2Cj%29%20%5Cin%20%5Cmathcal%7BE%7D&id=N6cLX)的边的集合。
- 接着为各条边创建要传递给节点
的消息,即实现
函数。
**MessagePassing.message(...)**函数接受最初传递给**MessagePassing.propagate(edge_index, size=None, **kwargs)**函数的所有参数。- 此外,传递给
propagate()的张量可以被映射到各自的节点和
上,只需在变量名后面加上
**_i**或**_j**。我们把称为消息传递的目标中心节点,把
称为邻接节点。
- 首先确定要给节点
MessagePassing.aggregate(...):- 将从源节点传递过来的消息聚合在目标节点上,一般可选的聚合方式有
sum,mean和max。
- 将从源节点传递过来的消息聚合在目标节点上,一般可选的聚合方式有
MessagePassing.message_and_aggregate(...):- 在一些场景里,邻接节点信息变换和邻接节点信息聚合这两项操作可以融合在一起,那么我们可以在此函数里定义这两项操作,从而让程序运行更加高效。
[MessagePassing.update(aggr_out, ...)](https://pytorch-geometric.readthedocs.io/en/latest/modules/nn.html#torch_geometric.nn.conv.message_passing.MessagePassing.update):- 为每个节点
更新节点表征,即实现
函数。该函数以聚合函数的输出为第一个参数,并接收所有传递给
propagate()函数的参数。
- 为每个节点
2.2.1 MessagePassing基类执行过程分析
在__init__()方法中,我们看到程序会检查子类是否实现了**message_and_aggregate()**方法,并将检查结果赋值给**fuse**属性。
class MessagePassing(torch.nn.Module):
def __init__(self, aggr: Optional[str] = "add", flow: str = "source_to_target", node_dim: int = -2):
super(MessagePassing, self).__init__()
# 此处省略n行代码
# Support for "fused" message passing.
self.fuse = self.inspector.implements('message_and_aggregate')
# 此处省略n行代码
“消息传播过程”是从**propagate**方法被调用开始执行的,先来看下propagate方法的源码
def propagate(self, edge_index: Adj, size: Size = None, **kwargs):
r"""开始消息传播的初始调用。
Args:
edge_index (Tensor or SparseTensor): 定义了消息传播流。
当flow="source_to_target"时,节点`edge_index[0]`的信息将被发送到节点`edge_index[1]`,
反之当flow="target_to_source"时,节点`edge_index[1]`的信息将被发送到节点`edge_index[0]`
kwargs: 图其他属性或额外的数据。
"""
size = self.__check_input__(edge_index, size)
# Run "fused" message and aggregation (if applicable).
if (isinstance(edge_index, SparseTensor) and self.fuse
and not self.__explain__):
coll_dict = self.__collect__(self.__fused_user_args__, edge_index,
size, kwargs)
msg_aggr_kwargs = self.inspector.distribute(
'message_and_aggregate', coll_dict)
out = self.message_and_aggregate(edge_index, **msg_aggr_kwargs)
update_kwargs = self.inspector.distribute('update', coll_dict)
return self.update(out, **update_kwargs)
# Otherwise, run both functions in separation.
elif isinstance(edge_index, Tensor) or not self.fuse:
coll_dict = self.__collect__(self.__user_args__, edge_index, size,
kwargs)
msg_kwargs = self.inspector.distribute('message', coll_dict)
out = self.message(**msg_kwargs)
# For `GNNExplainer`, we require a separate message and aggregate
# procedure since this allows us to inject the `edge_mask` into the
# message passing computation scheme.
if self.__explain__:
edge_mask = self.__edge_mask__.sigmoid()
# Some ops add self-loops to `edge_index`. We need to do the
# same for `edge_mask` (but do not train those).
if out.size(self.node_dim) != edge_mask.size(0):
loop = edge_mask.new_ones(size[0])
edge_mask = torch.cat([edge_mask, loop], dim=0)
assert out.size(self.node_dim) == edge_mask.size(0)
out = out * edge_mask.view([-1] + [1] * (out.dim() - 1))
aggr_kwargs = self.inspector.distribute('aggregate', coll_dict)
out = self.aggregate(out, **aggr_kwargs)
update_kwargs = self.inspector.distribute('update', coll_dict)
return self.update(out, **update_kwargs)
propagate()方法首先检查**edge_index**是否为**SparseTensor**类型(是否用稀疏张量表示矩阵)以及子类是否实现了**message_and_aggregate()**方法,如是就执行子类的**message_and_aggregate**方法;否则依次执行子类的**message(), aggregate(), update()**三个方法。
2.3 继承MessagePassing的GCN层(重点)
GCN层的数学定义为
%7D%20%3D%20%5Csum%7Bj%20%5Cin%20%5Cmathcal%7BN%7D(i)%20%5Ccup%20%5C%7B%20i%20%5C%7D%7D%20%5Cfrac%7B1%7D%7B%5Csqrt%7B%5Cdeg(i)%7D%20%5Ccdot%20%5Csqrt%7B%5Cdeg(j)%7D%7D%20%5Ccdot%20%5Cleft(%20%5Cmathbf%7B%5CTheta%7D%20%5Ccdot%20%5Cmathbf%7Bx%7D_j%5E%7B(k-1)%7D%20%5Cright)%2C%0A#card=math&code=%5Cmathbf%7Bx%7D_i%5E%7B%28k%29%7D%20%3D%20%5Csum%7Bj%20%5Cin%20%5Cmathcal%7BN%7D%28i%29%20%5Ccup%20%5C%7B%20i%20%5C%7D%7D%20%5Cfrac%7B1%7D%7B%5Csqrt%7B%5Cdeg%28i%29%7D%20%5Ccdot%20%5Csqrt%7B%5Cdeg%28j%29%7D%7D%20%5Ccdot%20%5Cleft%28%20%5Cmathbf%7B%5CTheta%7D%20%5Ccdot%20%5Cmathbf%7Bx%7D_j%5E%7B%28k-1%29%7D%20%5Cright%29%2C%0A&id=huRer)
其中,相邻节点的特征首先通过权重矩阵进行转换,然后按节点的度进行归一化处理,最后进行聚合。这个公式可以分为以下几个步骤:
- 向邻接矩阵添加自环边。
- 线性转换节点特征矩阵。
- 计算归一化系数。
- 归一化
,即临接节点的节点表征。
- 将相邻节点特征聚合(采用”求和”聚合方式)。
步骤1-3通常是在消息传递发生之前计算的。步骤4-5可以使用MessagePassing基类处理,该层的实现代码如下
import torch
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import add_self_loops, degree
class GCNConv(MessagePassing):
def __init__(self, in_channels, out_channels):
super(GCNConv, self).__init__(aggr='add', flow='source_to_target')
# aggr='add' 表示采用”Add“聚合(第五步)
# flow='source_to_target' 表示消息从源节点传播到目标节点
self.lin = torch.nn.Linear(in_channels, out_channels)
def forward(self, x, edge_index):
# X [N,in_channels]
# edge [2, E]
# 1.向邻接矩阵添加自环边
edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
# 2.线性转化节点特征矩阵
x = self.lin(x)
# 3.计算归一化系数
row, col = edge_index
# 这里因为是无向图,所以用row,col都行
deg = degree(col, x.size(0), dtype=x.dtype) # 计算出所有节点的度,其中row表示计算出度,col表示计算入度
deg_inv_sqrt = deg.pow(-0.5)
norm = deg_inv_sqrt[row] * deg_inv_sqrt[col]
# 4-5.开始进行消息传播
return self.propagate(edge_index, x=x, norm=norm)
def measage(self, x_j, norm):
# x_j [E, out_channels]
# 4.标准化节点特征
# .view方法相当于numpy中的resize,用来改变矩阵结构,这里相当于把矩阵展开成了一个一维向量
return norm.view(-1, 1) * x_j
GCN层继承了MessagePassing并以”求和”作为邻域节点信息聚合方式。对GCN层代码的理解如下:
__init__():
这一部分主要是定义了一个线性变换的结构进行降维,具体逻辑在**forward()**中实现。这部分对应公式中的,输入维度为
(N, in_channels),输出维度为(N, out_channels),N是节点个数。def __init__(self, in_channels, out_channels): super(GCNConv, self).__init__(aggr='add') # "Add" aggregation. self.lin = torch.nn.Linear(in_channels, out_channels)forward():
GCN层的所有逻辑都发生在**forward()**方法中。其中,def forward(self, x, edge_index): # X [N,in_channels] # edge [2, E] # 1.向邻接矩阵添加自环边 edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0)) # 2.线性转化节点特征矩阵 x = self.lin(x) # 3.计算归一化系数 row, col = edge_index # 这里因为是无向图,所以用row,col都行 deg = degree(col, x.size(0), dtype=x.dtype) # 计算出所有节点的度,其中row表示计算出度,col表示计算入度 deg_inv_sqrt = deg.pow(-0.5) norm = deg_inv_sqrt[row] * deg_inv_sqrt[col] # 4-5.开始进行消息传播 return self.propagate(edge_index, x=x, norm=norm)- 首先使用
torch_geometric.utils.add_self_loops()函数向我们的边索引添加自循环边,即构造矩阵(步骤1)
- 调用
torch.nn.Linear实例对节点特征进行线性变换(步骤2),变换的过程如下图所示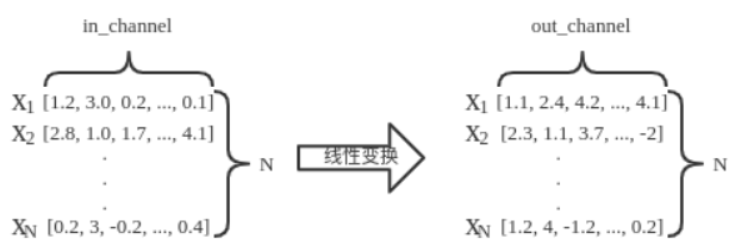
- 归一化系数是由每个节点的节点度得出的,它被转换为每个边的节点度。结果被保存在形状
**[num_edges, ]**的张量**norm**中(步骤3)
- 首先使用
message():
在message()函数中,我们需要通过**norm**对相邻节点表征进行归一化处理。这里,
**x_j**包含每条边的目标节点特征,即每个中心节点的邻接。
这里需要先说明一下x_j的由来。def measage(self, x_j, norm): # x_j [E, out_channels] # 4.标准化节点特征 # .view方法相当于numpy中的resize,用来改变矩阵结构,这里相当于把矩阵展开成了一个一维向量 return norm.view(-1, 1) * x_j- 边矩阵
edge_index,形状为(2, E),第一行表示边的source节点,第二行表示边的target节点,如下图所示: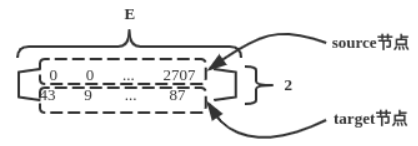
- 以target节点作为索引,从线性变换后的特征矩阵中索引得到target节点的特征矩阵,如下图所示:
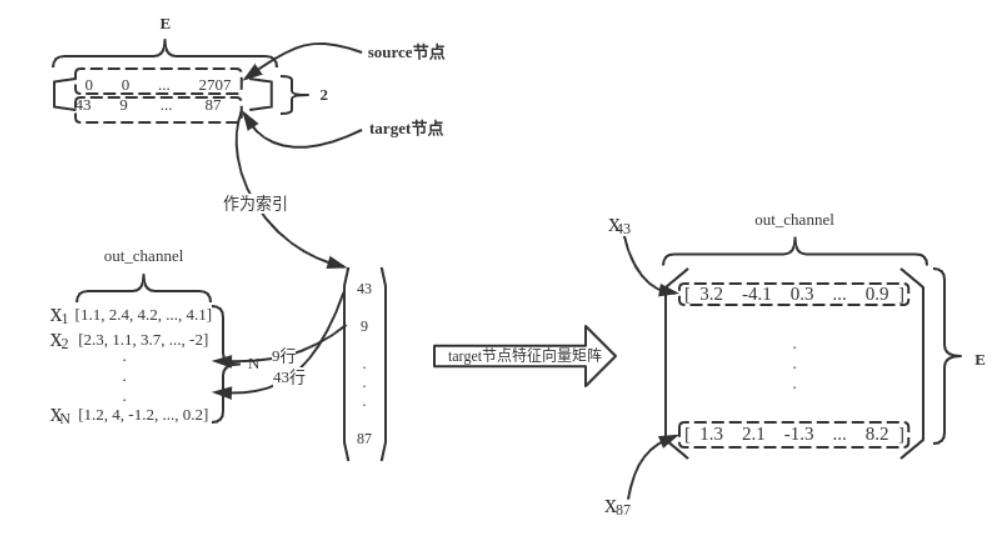
- 边矩阵
这就是x_j的由来,也是为什么形状为(E, out_channels)的原因。
aggregate():aggregate()函数按照source节点对target特征向量矩阵进行信息聚合,这里的聚合,就是source索引相同的target特征向量求和,用于得到source节点新的特征向量。示意图如下: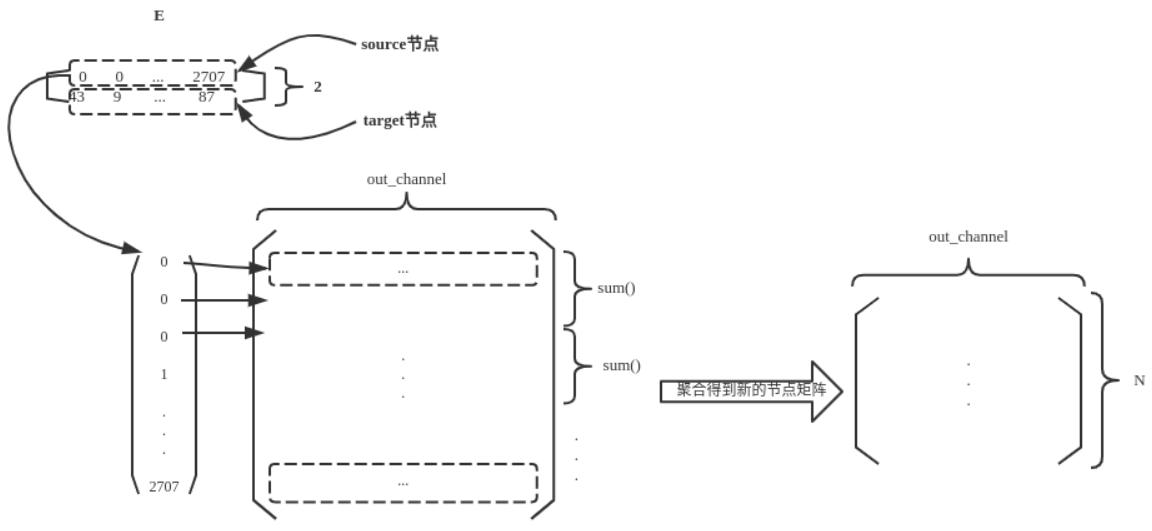
至此,就得到了该GCN层的输出,shape为(N, out_channel)。
以上就是创建一个仅包含一次“消息传递过程”的图神经网络的方法及对代码的理解。我们可以把这个层作为深层架构的构建块,方便地初始化和调用它:
conv = GCNConv(16, 32)
x = conv(x, edge_index)
通过串联多个这样的简单图神经网络,我们就可以构造复杂的图神经网络模型。
2.3.1 重写message方法
前面我们介绍了,传递给**propagate()**方法的参数,如果是节点的属性的话,可以被拆分成属于中心节点的部分和属于邻接节点的部分,只需在变量名后面加上**_i**或**_j**。现在我们有一个额外的节点属性,节点的度**deg**,我们希望**meassge**方法还能接收中心节点的度,我们对前面**GCNConv**的**message**方法进行改造得到新的**GCNConv**类:
import torch
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import add_self_loops, degree
from torch_geometric.datasets import Planetoid
class GCNConv(MessagePassing):
def __init__(self, in_channels, out_channels):
super(GCNConv, self).__init__(aggr='add', flow='source_to_target')
# aggr='add' 表示采用”Add“聚合(第五步)
# flow='source_to_target' 表示消息从源节点传播到目标节点
self.lin = torch.nn.Linear(in_channels, out_channels)
def forward(self, x, edge_index):
# X [N,in_channels]
# edge [2,E]
# 1.向邻接矩阵添加自环边
edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
# 2.线性转化节点特征矩阵
x = self.lin(x)
# 3.计算归一化系数
row, col = edge_index
deg = degree(col, x.size(0), dtype=x.dtype)
deg_inv_sqrt = deg.pow(-0.5)
norm = deg_inv_sqrt[row] * deg_inv_sqrt[col]
# 4-5.开始进行消息传播,这里增加了deg参数
return self.propagate(edge_index, x=x, norm=norm, deg=deg.view((-1, 1)))
def measage(self, x_j, norm, deg_i):
# x_j [E, out_channels]
# deg_i [E, 1]
# 4.标准化节点特征
return norm.view(-1, 1) * x_j * deg_i
dataset = Planetoid(root='/Dataset/', name='Cora')
data = dataset[0]
net = GCNConv(data.num_features, 64)
h_nodes = net(data.x, data.edge_index)
print(h_nodes.shape)
# torch.Size([2708, 64])
'''
原始数据的特征共1433维,可以看到,经过这一层GCNConv,数据的特征被映射到了64维
'''
若一个数据可以被拆分成属于中心节点的部分和属于邻接节点的部分,其形状必须是**[num_nodes, *]**,因此在上方代码的第29行,我们执行了deg.view((-1, 1))操作,使得数据形状为**[num_nodes, 1]**,然后才将数据传给propagate()方法。
2.3.2 重写aggregate方法
在前面的例子中,我们增加如下的aggregate函数,通过观察运行结果我们发现,我们重写的**aggregate**函数被调用,同时在**super(GCNConv, self).__init__(aggr='add')**中传递给**aggr**参数的值被存储到了**self.aggr**属性中。
import torch
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import add_self_loops, degree
from torch_geometric.datasets import Planetoid
class GCNConv(MessagePassing):
def __init__(self, in_channels, out_channels):
super(GCNConv, self).__init__(aggr='add', flow='source_to_target')
# aggr='add' 表示采用”Add“聚合(第五步)
# flow='source_to_target' 表示消息从源节点传播到目标节点
self.lin = torch.nn.Linear(in_channels, out_channels)
def forward(self, x, edge_index):
# X [N,in_channels]
# edge [2,E]
# 1.向邻接矩阵添加自环边
edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
# 2.线性转化节点特征矩阵
x = self.lin(x)
# 3.计算归一化系数
row, col = edge_index
deg = degree(col, x.size(0), dtype=x.dtype)
deg_inv_sqrt = deg.pow(-0.5)
norm = deg_inv_sqrt[row] * deg_inv_sqrt[col]
# 4-5.开始进行消息传播
return self.propagate(edge_index, x=x, norm=norm, deg=deg.view((-1, 1)))
def measage(self, x_j, norm, deg_i):
# x_j [E, out_channels]
# deg_i [E, 1]
# 4.标准化节点特征
return norm.view(-1, 1) * x_j * deg_i
def aggregate(self, inputs, index, ptr, dim_size):
print('self.aggr: ', self.aggr)
print("`aggregate` is called")
return super().aggregate(inputs, index, ptr=ptr, dim_size=dim_size)
dataset = Planetoid(root='/Dataset/', name='Cora')
data = dataset[0]
net = GCNConv(data.num_features, 64)
h_nodes = net(data.x, data.edge_index)
print(h_nodes.shape)
'''
self.aggr: add
`aggregate` is called
torch.Size([2708, 64])
'''
2.3.3 重写message_and_aggregate方法
在一些例子中,消息传递与消息聚合可以融合在一起,这种情况可以通过重写message_and_aggregate函数来实现,注意这里propagate()传入的不再是edge_index,而是SparseTensor类型的Adjancency Matrix。
import torch
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import add_self_loops, degree
from torch_sparse import SparseTensor
from torch_geometric.datasets import Planetoid
class GCNConv(MessagePassing):
def __init__(self, in_channels, out_channels):
super(GCNConv, self).__init__(aggr='add', flow='source_to_target')
# aggr='add' 表示采用”Add“聚合(第五步)
# flow='source_to_target' 表示消息从源节点传播到目标节点
self.lin = torch.nn.Linear(in_channels, out_channels)
def forward(self, x, edge_index):
# X [N,in_channels]
# edge [2,E]
# 1.向邻接矩阵添加自环边
edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
# 2.线性转化节点特征矩阵
x = self.lin(x)
# 3.计算归一化系数
row, col = edge_index
deg = degree(col, x.size(0), dtype=x.dtype)
deg_inv_sqrt = deg.pow(-0.5)
norm = deg_inv_sqrt[row] * deg_inv_sqrt[col]
# 4-5.开始进行消息传播
adjmat = SparseTensor(row=edge_index[0], col=edge_index[1], value=torch.ones(edge_index.shape[1]))
# 此处传的不再是edge_idex,而是SparseTensor类型的Adjancency Matrix
return self.propagate(adjmat, x=x, norm=norm, deg=deg.view((-1, 1)))
def measage(self, x_j, norm, deg_i):
# x_j [E, out_channels]
# deg_i [E, 1]
# 4.标准化节点特征
return norm.view(-1, 1) * x_j * deg_i
def aggregate(self, inputs, index, ptr, dim_size):
print('self.aggr: ', self.aggr)
print("`aggregate` is called")
return super().aggregate(inputs, index, ptr=ptr, dim_size=dim_size)
def message_and_aggregate(self, adj_t, x, norm):
print('`message_and_aggregate` is called')
# 没有实现真实的消息传递与消息聚合的操作
dataset = Planetoid(root='/Dataset/', name='Cora')
data = dataset[0]
net = GCNConv(data.num_features, 64)
h_nodes = net(data.x, data.edge_index)
# `message_and_aggregate` is called
运行程序后可以看到虽然我们同时重写了**message**函数和**aggregate**函数,然而只有**message_and_aggregate**函数被执行。
2.3.4 重写update函数
update函数接收聚合的输出作为第一个参数,此外还可以接收传递给propagate方法的任何参数。在下方的代码中,我们覆写的update方法接收了聚合的输出作为第一个参数,此外接收了传递给propagate的deg参数。
import torch
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import add_self_loops, degree
from torch_sparse import SparseTensor
from torch_geometric.datasets import Planetoid
class GCNConv(MessagePassing):
def __init__(self, in_channels, out_channels):
super(GCNConv, self).__init__(aggr='add', flow='source_to_target')
# aggr='add' 表示采用”Add“聚合(第五步)
# flow='source_to_target' 表示消息从源节点传播到目标节点
self.lin = torch.nn.Linear(in_channels, out_channels)
def forward(self, x, edge_index):
# X [N,in_channels]
# edge [2,E]
# 1.向邻接矩阵添加自环边
edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
# 2.线性转化节点特征矩阵
x = self.lin(x)
# 3.计算归一化系数
row, col = edge_index # 这里row表示源节点列表, col表示目标节点列表
deg = degree(col, x.size(0), dtype=x.dtype)
deg_inv_sqrt = deg.pow(-0.5)
norm = deg_inv_sqrt[row] * deg_inv_sqrt[col]
# 4-5.开始进行消息传播
adjmat = SparseTensor(row=edge_index[0], col=edge_index[1], value=torch.ones(edge_index.shape[1]))
# 此处传的不再是edge_idex,而是SparseTensor类型的Adjancency Matrix
return self.propagate(adjmat, x=x, norm=norm, deg=deg.view((-1, 1)))
def measage(self, x_j, norm, deg_i):
# x_j [E, out_channels]
# deg_i [E, 1]
# 4.标准化节点特征
return norm.view(-1, 1) * x_j * deg_i
def aggregate(self, inputs, index, ptr, dim_size):
print('self.aggr: ', self.aggr)
print("`aggregate` is called")
return super().aggregate(inputs, index, ptr=ptr, dim_size=dim_size)
def message_and_aggregate(self, adj_t, x, norm):
print('`message_and_aggregate` is called')
# 没有实现真实的消息传递与消息聚合的操作
def update(self, inputs, deg):
print(deg)
return inputs
dataset = Planetoid(root='/Dataset/', name='Cora')
data = dataset[0]
net = GCNConv(data.num_features, 64)
h_nodes = net(data.x, data.edge_index)
'''
`message_and_aggregate` is called
tensor([[4.],
[4.],
[6.],
...,
[2.],
[5.],
[5.]])
'''
2.4 继承MessagePassing的EdgeConv层
边卷积或者点云卷积在数学上被定义为:
%7D%20%3D%20%5Cmax%7B%5Cmathbf%7Bj%7D%20%5Cin%20%5Cmathbf%7BN(i)%7D%7D%5Cmathbf%7Bh%7D%7B%5CTheta%7D(%5Cmathbf%7Bx%7Di%5E%7B(k-1)%7D%2C%20%5Cmathbf%7Bx%7D_j%5E%7B(k-1)%7D-%5Cmathbf%7Bx%7D_i%5E%7B(k-1)%7D)%0A#card=math&code=%5Cmathbf%7Bx%7D_i%5E%7B%28k%29%7D%20%3D%20%5Cmax%7B%5Cmathbf%7Bj%7D%20%5Cin%20%5Cmathbf%7BN%28i%29%7D%7D%5Cmathbf%7Bh%7D_%7B%5CTheta%7D%28%5Cmathbf%7Bx%7D_i%5E%7B%28k-1%29%7D%2C%20%5Cmathbf%7Bx%7D_j%5E%7B%28k-1%29%7D-%5Cmathbf%7Bx%7D_i%5E%7B%28k-1%29%7D%29%0A&id=okNdv)
这里表示多层感知机。类比GCN层,也可以通过继承
MessagePassing类来实现,这里采用max方式聚合:
import torch
from torch.nn import Sequential as Seq, Linear, ReLU
from torch_geometric.nn import MessagePassing
class EdgeConv(MessagePassing):
def __init__(self, in_channels, out_channels):
super(EdgeConv, self).__init__(aggr='max') # "Max" aggregation.
self.mlp = Seq(Linear(2 * in_channels, out_channels),
ReLU(),
Linear(out_channels, out_channels))
def forward(self, x, edge_index):
# x 的形状为 [N, in_channels]
# edge_index 的形状为 [2, E]
return self.propagate(edge_index, x=x)
def message(self, x_i, x_j):
# x_i 的形状为 [E, in_channels]
# x_j 的形状为 [E, in_channels]
tmp = torch.cat([x_i, x_j - x_i], dim=1) # tmp 的形状为 [E, 2 * in_channels]
return self.mlp(tmp)
在message()函数内部,我们使用对每条边**self.mlp**的目标节点特征**x_i**和相对源节点特征进行变换%E2%88%88E#card=math&code=x_j%20-%20x_i%2C%20%28j%2Ci%29%E2%88%88E&id=cRIM0)。
边卷积实际上是一种动态卷积,它使用特征空间中的最近邻重新计算每一层的图。PyG 带有 GPU 加速的批处理 k-NN 图生成方法torch_geometric.nn.pool.knn_graph():
from torch_geometric.nn import knn_graph
class DynamicEdgeConv(EdgeConv):
def __init__(self, in_channels, out_channels, k=6):
super(DynamicEdgeConv, self).__init__(in_channels, out_channels)
self.k = k
def forward(self, x, batch=None):
edge_index = knn_graph(x, self.k, batch, loop=False, flow=self.flow)
return super(DynamicEdgeConv, self).forward(x, edge_index)
在这里,knn_graph()计算最近邻图,它进一步用于调用 的forward()方法EdgeConv。
同样的,也可以通过一个接口来初始化和调用该层
conv = DynamicEdgeConv(3, 128, k=6)
x = conv(x, batch)
3. 作业
3.1 总结MessagePassing类的运行流程
MessagePassing类的流程主要分为如下两个步骤,从邻居节点聚集信息,然后用神经网络更新节点表示,可以用如下两个公式表示
%7D%7BMt(h_v%5Et%2C%20h_w%5Et%2C%20c%7Bvw%7D)%7D%0A#card=math&code=mv%5E%7Bt%2B1%7D%20%3D%20%5Csum%7Bw%20%5Cin%20N%28v%29%7D%7BMt%28h_v%5Et%2C%20h_w%5Et%2C%20c%7Bvw%7D%29%7D%0A&id=XiRzg)
%0A#card=math&code=h_v%5E%7Bt%2B1%7D%20%3D%20U_t%28h_v%5Et%2C%20m_v%5E%7Bt%2B1%7D%29%0A&id=Wuoy4)
3.2 请复现一个一层的图神经网络的构造,总结通过继承MessagePassing基类来构造自己的图神经网络类的规范
这里我选择实现一个未使用归一化的增加自环边的GCNConv层,并输出线性变换后的x, x_j以及结果的大小,其数学公式如下:
%7D%7D%20%3D%20%5Cmathbf%7B%5Chat%7BA%7D%7D%0A%5Cmathbf%7BH%5E%7B(l)%7D%7D%20%5Cmathbf%7BW%7D%2C%0A#card=math&code=%5Cmathbf%7BH%5E%7B%28l%2B1%29%7D%7D%20%3D%20%5Cmathbf%7B%5Chat%7BA%7D%7D%0A%5Cmathbf%7BH%5E%7B%28l%29%7D%7D%20%5Cmathbf%7BW%7D%2C%0A&id=NH0FX)
反映到节点上则是:
%7Di%20%3D%20%5Cmathbf%7BW%7D%20%5Csum%7Bj%20%5Cin%20%5Cmathcal%7BN%7D(v)%20%5Ccup%0A%5C%7B%20i%20%5C%7D%7D%20e%7Bj%2Ci%7D%20%5Cmathbf%7Bx%7D_j%5E%7B(l)%7D%0A#card=math&code=%5Cmathbf%7Bx%7D%5E%7B%28l%2B1%29%7D_i%20%3D%20%5Cmathbf%7BW%7D%20%5Csum%7Bj%20%5Cin%20%5Cmathcal%7BN%7D%28v%29%20%5Ccup%0A%5C%7B%20i%20%5C%7D%7D%20e_%7Bj%2Ci%7D%20%5Cmathbf%7Bx%7D_j%5E%7B%28l%29%7D%0A&id=ZJ19V)
和之前介绍的GCNconv类似,这个公式也可以分为如下几步:
- 向邻接矩阵添加自环边。
- 线性转换节点特征矩阵。
- 将相邻节点特征聚合(采用”求和”聚合方式)。
代码如下:
import torch
from torch.nn import Linear
from torch_geometric.utils import add_self_loops
from torch_geometric.nn import MessagePassing
from torch_geometric.datasets import Planetoid
class MyGNN(MessagePassing):
def __init__(self, in_channels, out_channels):
super(MyGNN, self).__init__(aggr='add', flow='source_to_target')
self.lin = Linear(in_channels, out_channels)
def forward(self, x, edge_index):
# X [N,in_channels]
# edge [2, E]
# 1.向邻接矩阵添加自环边
edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
# 2.线性转化节点特征矩阵
x = self.lin(x)
print("X Shape ",x.shape)
# X [N,out_channels]
# 3.开始进行消息传播
return self.propagate(edge_index, x=x)
def message(self, x_j):
print("X_j Shape ",x_j.shape)
return x_j
def aggregate(self, inputs, index, ptr, dim_size):
# print('self.aggr: ', self.aggr)
return super().aggregate(inputs, index)
def update(self, inputs):
print("Result Shape ", inputs.shape)
return inputs
dataset = Planetoid(root='/Dataset/', name='Cora')
data = dataset[0]
net = MyGNN(data.num_features, 64)
result = net(data.x, data.edge_index)
'''
X Shape torch.Size([2708, 64])
X_j Shape torch.Size([13264, 64])
Result Shape torch.Size([2708, 64])
'''

