Task05 超大图上的节点表征学习

引言

本节我们基于论文Cluster-GCN: An Efficient Algorithm for Training Deep and Large Graph Convolutional Network介绍超大图上的节点表征学习。

1. 产生背景

目前，基于随机梯度下降（SGD）的训练方法在大规模图卷积神经网络上需要很大的计算量，且随着GCN层的层数呈指数级增长。此外，保存整个图的信息和每一层每个节点的表征到内存（显存）而消耗巨大内存（显存）空间。虽然已经有一些论文提出了无需保存整个图的信息和每一层每个节点的表征到GPU内存（显存）的方法（比如GraphSAGE采用采样的方法），但这些方法可能会损失预测精度或者对提高内存的利用率并不明显。为了解决普通的训练方法无法训练超大图的问题，论文提出了一种新的图神经网络的训练方法：Cluster-GCN，该方法的主要思想和优势如下：

• 利用图节点聚类算法将一个图的节点划分为个簇，每一次选择几个簇的节点和这些节点对应的边构成一个子图，然后对子图做训练。
• 由于是利用图节点聚类算法将节点划分为多个簇，所以簇内边的数量要比簇间边的数量多得多，这样可以提高表征利用率，并提高图神经网络的训练效率。
• 每一次随机选择多个簇来组成一个batch，这样不会丢失簇间的边，同时也不会有batch内类别分布偏差过大的问题。
• 基于小图进行训练，不会消耗很多内存空间，于是我们可以训练更深的神经网络，进而可以达到更高的精度。

2. 模型原理

2.1 节点表征学习回顾

给定一个图#card=math&code=G%3D%28%5Cmathcal%7BV%7D%2C%20%5Cmathcal%7BE%7D%2C%20A%29&id=fbiqN)，它由个节点和条边组成，其邻接矩阵记为，其节点属性记为，表示节点属性的维度。一个层的图卷积神经网络由个图卷积层组成，每一层都通过聚合邻接节点的上一层的表征来生成中心节点的当前层的表征：

%7D%3DA%5E%7B%5Cprime%7D%20X%5E%7B(l)%7D%20W%5E%7B(l)%7D%2C%20%5C%20X%5E%7B(l%2B1)%7D%3D%5Csigma%5Cleft(Z%5E%7B(l%2B1)%7D%5Cright)%0A%5Ctag%7B1%7D%0A#card=math&code=Z%5E%7B%28l%2B1%29%7D%3DA%5E%7B%5Cprime%7D%20X%5E%7B%28l%29%7D%20W%5E%7B%28l%29%7D%2C%20%5C%20X%5E%7B%28l%2B1%29%7D%3D%5Csigma%5Cleft%28Z%5E%7B%28l%2B1%29%7D%5Cright%29%0A%5Ctag%7B1%7D%0A&id=rOsSS)

其中%7D%20%5Cin%20%5Cmathbb%7BR%7D%5E%7BN%20%5Ctimes%20F%7Bl%7D%7D#card=math&code=X%5E%7B%28l%29%7D%20%5Cin%20%5Cmathbb%7BR%7D%5E%7BN%20%5Ctimes%20F%7Bl%7D%7D&id=SqztB)表示第层个节点的表征，并且有%7D%3DX#card=math&code=X%5E%7B%280%29%7D%3DX&id=DKsDT)。是归一化和规范化后的邻接矩阵，%7D%20%5Cin%20%5Cmathbb%7BR%7D%5E%7BF%7Bl%7D%20%5Ctimes%20F%7Bl%2B1%7D%7D#card=math&code=W%5E%7B%28l%29%7D%20%5Cin%20%5Cmathbb%7BR%7D%5E%7BF%7Bl%7D%20%5Ctimes%20F%7Bl%2B1%7D%7D&id=PGxk7)是权重矩阵，也就是要训练的参数。为了简单起见，我们假设所有层的表征维度都是一样的，即 #card=math&code=%5Cleft%28F%7B1%7D%3D%5Ccdots%3DF%7BL%7D%3DF%5Cright%29&id=Sjlfo)。激活函数#card=math&code=%5Csigma%28%5Ccdot%29&id=N9UyN)通常被设定为ReLU。

当图神经网络应用于半监督节点分类任务时，训练的目标是通过最小化损失函数来学习公式(1)中的权重矩阵：

%7D%5Cright)%0A%5Ctag%7B2%7D%0A#card=math&code=%5Cmathcal%7BL%7D%3D%5Cfrac%7B1%7D%7B%5Cleft%7C%5Cmathcal%7BY%7D%7BL%7D%5Cright%7C%7D%20%5Csum%7Bi%20%5Cin%20%5Cmathcal%7BY%7D%7BL%7D%7D%20%5Coperatorname%7Bloss%7D%5Cleft%28y%7Bi%7D%2C%20z_%7Bi%7D%5E%7B%28L%29%7D%5Cright%29%0A%5Ctag%7B2%7D%0A&id=HNNSP)

其中，是节点类别；%7D#card=math&code=z%7Bi%7D%5E%7B%28L%29%7D&id=l7wdm)是%7D#card=math&code=Z%5E%7B%28L%29%7D&id=t63kt)的第行，表示对节点的预测，节点的真实类别为。

2.2 Cluster-GCN方法

2.2.1 以往方法的缺陷

以往的训练方法需要同时计算所有节点的表征以及训练集中所有节点的损失产生的梯度（后文我们直接称为完整梯度）。这种训练方式需要非常巨大的计算开销和内存（显存）开销：在内存（显存）方面，计算上一节中公式(2)的完整梯度需要存储所有的节点表征矩阵%7D%5Cright%5C%7D%7Bl%3D1%7D%5E%7BL%7D#card=math&code=%5Cleft%5C%7BZ%5E%7B%28l%29%7D%5Cright%5C%7D%7Bl%3D1%7D%5E%7BL%7D&id=gieMI)，这需要#card=math&code=O%28N%20F%20L%29&id=v31eP)的空间；在收敛速度方面，由于神经网络在每个epoch中只更新一次，所以训练需要更多的epoch才能达到收敛。

最近的一些工作证明，采用mini-batch SGD的方式训练，可以提高图神经网络的训练速度并减少内存（显存）需求。在参数更新中，SGD不需要计算完整梯度，而只需要基于mini-batch计算部分梯度。我们使用来表示一个batch，其大小为。SGD的每一步都将计算梯度估计值%7D%5Cright)#card=math&code=%5Cfrac%7B1%7D%7B%7C%5Cmathcal%7BB%7D%7C%7D%20%5Csum%7Bi%20%5Cin%20%5Cmathcal%7BB%7D%7D%20%5Cnabla%20%5Coperatorname%7Bloss%7D%5Cleft%28y%7Bi%7D%2C%20z_%7Bi%7D%5E%7B%28L%29%7D%5Cright%29&id=sZiSZ)来进行参数更新。尽管在epoches数量相同的情况下，采用SGD方式进行训练，收敛速度可以更快，但此种训练方式会引入额外的时间开销，这使得相比于全梯度下降的训练方式，此种训练方式每个epoch的时间开销要大得多。

为什么采用最简单的mini-batch SGD方式进行训练，每个epoch需要的时间更多？

• 我们将节点的梯度的计算表示为%7D%5Cright)#card=math&code=%5Cnabla%20%5Coperatorname%7Bloss%7D%5Cleft%28y%7Bi%7D%2C%20z%7Bi%7D%5E%7B%28L%29%7D%5Cright%29&id=jhUE1)，它依赖于节点的层的表征，而节点的非第层的表征都依赖于各自邻接节点的前一层的表征，这被称为邻域扩展。假设一个图神经网络有层，节点的平均的度为。为了得到节点的梯度，平均我们需要聚合图上#card=math&code=O%5Cleft%28d%5E%7BL%7D%5Cright%29&id=q6685)的节点的表征（节点度为，即每层要聚集个节点的信息，共L+1层，抛开最开始一层，共需要聚集次，所以为）。也就是说，我们需要获取节点的距离为#card=math&code=k%28k%3D1%2C%20%5Ccdots%2C%20L%29&id=w9YES)的邻接节点的信息来进行一次参数更新。由于要与权重矩阵%7D#card=math&code=W%5E%7B%28l%29%7D&id=z3xvh)相乘，所以计算任意节点表征的时间开销是#card=math&code=O%5Cleft%28F%5E%7B2%7D%5Cright%29&id=TwxqO)。所以平均来说，一个节点的梯度的计算需要#card=math&code=O%5Cleft%28d%5E%7BL%7D%20F%5E%7B2%7D%5Cright%29&id=Dxpm5)的时间。

节点表征的利用率可以反映出计算的效率。考虑到一个batch有多个节点，时间与空间复杂度的计算就不是上面那样简单了，因为不同的节点同样距离远的邻接节点可以是重叠的，于是计算表征的次数可以小于最坏的情况#card=math&code=O%5Cleft%28b%20d%5E%7BL%7D%5Cright%29&id=j6fts)。为了反映mini-batch SGD的计算效率，Cluster-GCN论文提出了“表征利用率”的概念来描述计算效率。在训练过程中，如果节点在层的表征%7D#card=math&code=z%7Bi%7D%5E%7B%28l%29%7D&id=cqiU7)被计算并在层的表征计算中被重复使用次，那么我们说%7D#card=math&code=z_%7Bi%7D%5E%7B%28l%29%7D&id=UmXIt)的表征利用率为。对于随机抽样的mini-batch SGD，非常小，因为图通常是大且稀疏的。假设是一个小常数（节点间同样距离的邻接节点重叠率小），那么mini-batch SGD的训练方式对每个batch需要计算#card=math&code=O%5Cleft%28b%20d%5E%7BL%7D%5Cright%29&id=qT96B)的表征，于是每次参数更新需要#card=math&code=O%5Cleft%28b%20d%5E%7BL%7D%20F%5E%7B2%7D%5Cright%29&id=VCX9u)的时间，每个epoch需要#card=math&code=O%5Cleft%28N%20d%5E%7BL%7D%20F%5E%7B2%7D%5Cright%29&id=n3354)的时间，这被称为邻域扩展问题。

相反的是，全梯度下降训练具有最大的表征利用率——每个节点表征将在上一层被重复使用平均节点度次。因此，全梯度下降法在每个epoch中只需要计算#card=math&code=O%28N%20L%29&id=LCxts)的表征，这意味着平均下来只需要#card=math&code=O%28L%29&id=gx1ds)的表征计算就可以获得一个节点的梯度。

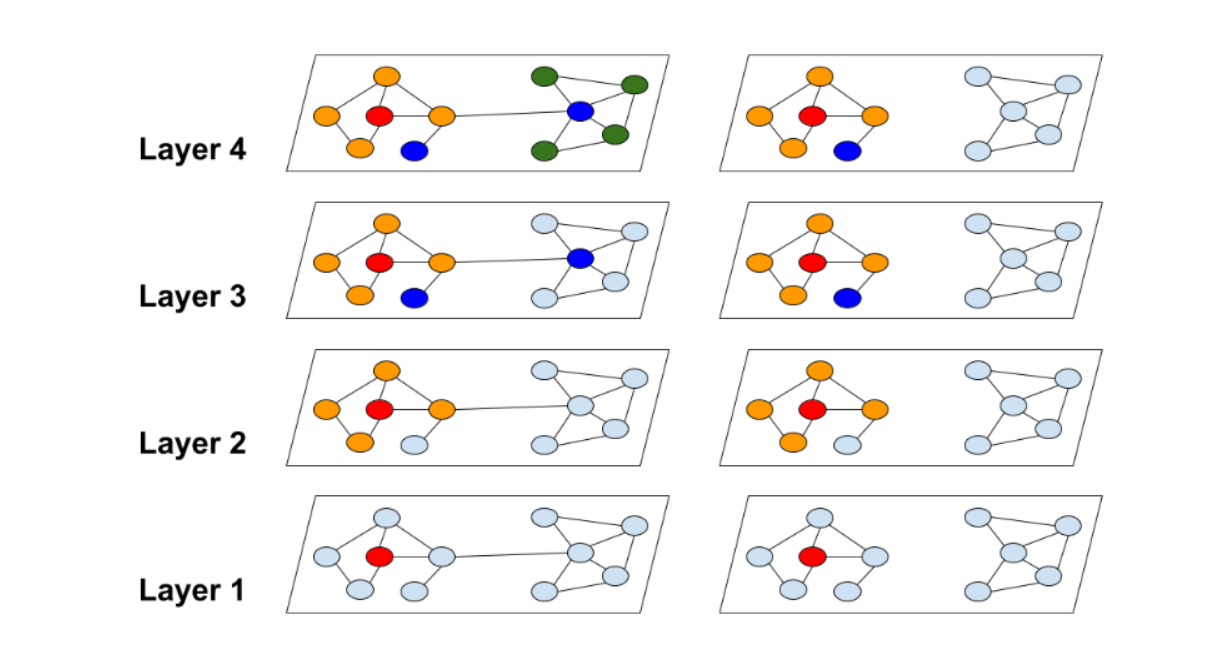
下图展示了过去的方法和Cluster-GCN方法之间的邻域扩展差异。红色节点是邻域扩展的起始节点。过去的方法需要做指数级的邻域扩展（图左），而Cluster-GCN的方法可以避免巨大范围的邻域扩展（图右）。

2.2.2 Cluster-GCN方法原理

Cluster-GCN方法是由这样的问题驱动的：

• 我们能否找到一种将节点分成多个batch的方式，对应地将图划分成多个子图，使得表征利用率最大？

我们通过将表征利用率的概念与图节点聚类的目标联系起来来回答这个问题。

考虑到在每个batch中，我们计算一组节点（记为）从第层到第层的表征。由于图神经网络每一层的计算都使用相同的子图（内部的边），所以表征利用率就是这个batch内边的数量，记为。因此，为了最大限度地提高表征利用率，理想的划分batch的结果是，batch内的边尽可能多，batch之间的边尽可能少。基于这一点，我们将SGD图神经网络训练的效率与图聚类算法联系起来。

现在我们正式学习Cluster-GCN方法。对于一个图，我们将其节点划分为个簇：，其中由第个簇中的节点组成，对应的我们有个子图：

其中只由中的节点之间的边组成。经过节点重组，邻接矩阵被划分为大小为的块矩阵，如下所示

其中

其中，对角线上的块是大小为的邻接矩阵，它由内部的边构成。是图的邻接矩阵。由两个簇和之间的边构成。是由的所有非对角线块组成的矩阵。同样，我们可以根据划分节点表征矩阵和类别向量，得到和，其中和分别由中节点的表征和类别组成。

接下来我们用块对角线邻接矩阵去近似邻接矩阵，这样做的好处是，完整的损失函数（公式(2）)可以根据batch分解成多个部分之和。以表示归一化后的，最后一层节点表征矩阵可以做如下的分解：

%7D%20%26%3D%5Cbar%7BA%7D%5E%7B%5Cprime%7D%20%5Csigma%5Cleft(%5Cbar%7BA%7D%5E%7B%5Cprime%7D%20%5Csigma%5Cleft(%5Ccdots%20%5Csigma%5Cleft(%5Cbar%7BA%7D%5E%7B%5Cprime%7D%20X%20W%5E%7B(0)%7D%5Cright)%20W%5E%7B(1)%7D%5Cright)%20%5Ccdots%5Cright)%20W%5E%7B(L-1)%7D%20%5C%5C%0A%26%3D%5Cleft%5B%5Cbegin%7Barray%7D%7Bc%7D%0A%5Cbar%7BA%7D%7B11%7D%5E%7B%5Cprime%7D%20%5Csigma%5Cleft(%5Cbar%7BA%7D%7B11%7D%5E%7B%5Cprime%7D%20%5Csigma%5Cleft(%5Ccdots%20%5Csigma%5Cleft(%5Cbar%7BA%7D%7B11%7D%5E%7B%5Cprime%7D%20X%7B1%7D%20W%5E%7B(0)%7D%5Cright)%20W%5E%7B(1)%7D%5Cright)%20%5Ccdots%5Cright)%20W%5E%7B(L-1)%7D%20%5C%5C%0A%5Cvdots%20%5C%5C%0A%5Cbar%7BA%7D%7Bc%20c%7D%5E%7B%5Cprime%7D%20%5Csigma%5Cleft(%5Cbar%7BA%7D%7Bc%20c%7D%5E%7B%5Cprime%7D%20%5Csigma%5Cleft(%5Ccdots%20%5Csigma%5Cleft(%5Cbar%7BA%7D%7Bc%20c%7D%5E%7B%5Cprime%7D%20X%7Bc%7D%20W%5E%7B(0)%7D%5Cright)%20W%5E%7B(1)%7D%5Cright)%20%5Ccdots%5Cright)%20W%5E%7B(L-1)%7D%0A%5Cend%7Barray%7D%5Cright%5D%0A%5Cend%7Baligned%7D%0A%5Ctag%7B6%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AZ%5E%7B%28L%29%7D%20%26%3D%5Cbar%7BA%7D%5E%7B%5Cprime%7D%20%5Csigma%5Cleft%28%5Cbar%7BA%7D%5E%7B%5Cprime%7D%20%5Csigma%5Cleft%28%5Ccdots%20%5Csigma%5Cleft%28%5Cbar%7BA%7D%5E%7B%5Cprime%7D%20X%20W%5E%7B%280%29%7D%5Cright%29%20W%5E%7B%281%29%7D%5Cright%29%20%5Ccdots%5Cright%29%20W%5E%7B%28L-1%29%7D%20%5C%5C%0A%26%3D%5Cleft%5B%5Cbegin%7Barray%7D%7Bc%7D%0A%5Cbar%7BA%7D%7B11%7D%5E%7B%5Cprime%7D%20%5Csigma%5Cleft%28%5Cbar%7BA%7D%7B11%7D%5E%7B%5Cprime%7D%20%5Csigma%5Cleft%28%5Ccdots%20%5Csigma%5Cleft%28%5Cbar%7BA%7D%7B11%7D%5E%7B%5Cprime%7D%20X%7B1%7D%20W%5E%7B%280%29%7D%5Cright%29%20W%5E%7B%281%29%7D%5Cright%29%20%5Ccdots%5Cright%29%20W%5E%7B%28L-1%29%7D%20%5C%5C%0A%5Cvdots%20%5C%5C%0A%5Cbar%7BA%7D%7Bc%20c%7D%5E%7B%5Cprime%7D%20%5Csigma%5Cleft%28%5Cbar%7BA%7D%7Bc%20c%7D%5E%7B%5Cprime%7D%20%5Csigma%5Cleft%28%5Ccdots%20%5Csigma%5Cleft%28%5Cbar%7BA%7D%7Bc%20c%7D%5E%7B%5Cprime%7D%20X%7Bc%7D%20W%5E%7B%280%29%7D%5Cright%29%20W%5E%7B%281%29%7D%5Cright%29%20%5Ccdots%5Cright%29%20W%5E%7B%28L-1%29%7D%0A%5Cend%7Barray%7D%5Cright%5D%0A%5Cend%7Baligned%7D%0A%5Ctag%7B6%7D%0A&id=W2uNb)

由于是块对角形式（是的对角线上的块），于是损失函数可以分解为

%7D%5Cright)%0A%5Ctag%7B7%7D%0A#card=math&code=%5Cmathcal%7BL%7D%7B%5Cbar%7BA%7D%5E%7B%5Cprime%7D%7D%3D%5Csum%7Bt%7D%20%5Cfrac%7B%5Cleft%7C%5Cmathcal%7BV%7D%7Bt%7D%5Cright%7C%7D%7BN%7D%20%5Cmathcal%7BL%7D%7B%5Cbar%7BA%7D%7Bt%20t%7D%5E%7B%5Cprime%7D%7D%20%5Ctext%20%7B%20and%20%7D%20%5Cmathcal%7BL%7D%7B%5Cbar%7BA%7D%7Bt%20t%7D%5E%7B%5Cprime%7D%7D%3D%5Cfrac%7B1%7D%7B%5Cleft%7C%5Cmathcal%7BV%7D%7Bt%7D%5Cright%7C%7D%20%5Csum%7Bi%20%5Cin%20%5Cmathcal%7BV%7D%7Bt%7D%7D%20%5Coperatorname%7Bloss%7D%5Cleft%28y%7Bi%7D%2C%20z%7Bi%7D%5E%7B%28L%29%7D%5Cright%29%0A%5Ctag%7B7%7D%0A&id=ydOVE)

基于公式(6)和公式(7)，在训练的每一步中，Cluster-GCN首先采样一个簇，然后根据的梯度进行参数更新。这种训练方式，只需要用到子图, , 以及神经网络权重矩阵%7D%5Cright%5C%7D%7Bl%3D1%7D%5E%7BL%7D#card=math&code=%5Cleft%5C%7BW%5E%7B%28l%29%7D%5Cright%5C%7D%7Bl%3D1%7D%5E%7BL%7D&id=szqv3)。 实际中，主要的计算开销在神经网络前向过程中的矩阵乘法运算（公式(6)的一个行）和梯度反向传播。

我们使用图节点聚类算法来划分图。图节点聚类算法将图节点分成多个簇，划分结果是簇内边的数量远多于簇间边的数量。如前所述，每个batch的表征利用率相当于簇内边的数量。直观地说，每个节点和它的邻接节点大部分情况下都位于同一个簇中，因此跳（L-hop）远的邻接节点大概率仍然在同一个簇中。由于我们用块对角线近似邻接矩阵代替邻接矩阵，产生的误差与簇间的边的数量成正比，所以簇间的边越少越好。综上所述，使用图节点聚类算法对图节点划分多个簇的结果，正是我们希望得到的。

回看上一节最后的图，很明显，Cluster-GCN方法可以避免巨大范围的邻域扩展（图右），因为Cluster-GCN方法将邻域扩展限制在簇内。

2.2.2.1 时间与空间复杂度分析

由于簇中每个节点只连接到该簇内部的节点，节点的邻域扩展不需要在簇外进行。每个batch的计算将纯粹是矩阵乘积运算（%7D%20W%5E%7B(l)%7D#card=math&code=%5Cbar%7BA%7D%7Bt%20t%7D%5E%7B%5Cprime%7D%20X%7Bt%7D%5E%7B%28l%29%7D%20W%5E%7B%28l%29%7D&id=avLp4)）和一些对元素的操作（ReLU），因此每个batch的总体时间复杂度为#card=math&code=O%5Cleft%28%5Cleft%5C%7CA%7Bt%20t%7D%5Cright%5C%7C%7B0%7D%20F%2B%20b%20F%5E%7B2%7D%5Cright%29&id=BtaiL)。因此，每个epoch的总体时间复杂度为#card=math&code=O%5Cleft%28%5C%7CA%5C%7C_%7B0%7D%20F%2BN%20F%5E%7B2%7D%5Cright%29&id=oOzLN)。平均来说，每个batch只需要计算#card=math&code=O%28b%20L%29&id=jqIWQ)的表征，这是线性的，而不是指数级的。在空间复杂度方面，在每个batch中，我们只需要在每一层中存储个节点的表征，产生用于存储表征的内存（显存）开销为#card=math&code=O%28b%20L%20F%29&id=RPjoD)。因此，此算法也比之前所有的算法的内存效率更高。此外，我们的算法只需加载子图到内存（显存）中，而不是完整的图（尽管图的存储通常不是内存瓶颈）。下表中总结了详细的时间和内存复杂度。

2.2.3 随机多分区

尽管简单Cluster-GCN方法可以做到较其他方法更低的计算和内存复杂度，但它仍存在两个潜在问题：

• 图被分割后，一些边（公式(4)中的部分）被移除，性能可能因此会受到影响。
• 图聚类算法倾向于将相似的节点聚集在一起。因此，单个簇中节点的类别分布可能与原始数据集不同，导致对梯度的估计有偏差。

下图展示了一个类别分布不平衡的例子，采用Reddit数据集，节点聚类由Metis软件包实现。根据各个簇的类别分布来计算熵值。与随机划分相比，采用聚类划分得到的大多数簇熵值都很小，簇熵值小表明簇中节点的标签分布偏向于某一些特定的类别，这意味着不同簇的标签分布有较大的差异，这将影响训练的收敛。

为了解决上述问题，Cluster-GCN论文提出了一种随机多簇方法，此方法首先将图划分为个簇，，是一个较大的值，在构建一个batch时，不是只使用一个簇，而是使用随机选择的个簇，表示为，得到的batch包含节点 、簇内边和簇间边。此方法的好处有，

1）不会丢失簇间的边;

2）不会有很大的batch内类别分布的偏差;

3）以及不同的epoch使用的batch不同，这可以降低梯度估计的偏差。

下图展示了随机多簇方法，在每个epoch中，采取不放回的方式随机选择个簇（这里=2）及簇间的边来组成一个batch（相同颜色的色块在同一Batch中），不同的epoch的batch不同。这里对角线上的矩阵代表了簇内边，非对角线上的矩阵表示簇间边。

如下图所示，使用多个簇来组成一个batch可以提高收敛性。

这里，虚线部分使用300个簇，实线部分使用1500个簇，并随机选择5个簇来组成一个batch。该图X轴为epoches，Y轴为F1-Score。

最终的Cluster-GCN算法如下图所示，

2.2.4 训练深层GCNs的问题

以往尝试训练更深的GCN的研究似乎表明，增加更多的层是没有帮助的。然而，那些研究的实验使用的图太小，所以结论可能并不正确。例如，其中有一项研究只使用了一个只有几百个训练节点的图，由于节点数量过少，很容易出现过拟合的问题。此外，加深GCN神经网络层数后，训练变得很困难，因为层数多了之后前面的信息可能无法传到后面。有的研究采用了一种类似于残差连接的技术，使模型能够将前一层的信息直接传到下一层。具体来说，他们修改了公式(1)，将第层的表征添加到下一层，如下所示

%7D%3D%5Csigma%5Cleft(A%5E%7B%5Cprime%7D%20X%5E%7B(l)%7D%20W%5E%7B(l)%7D%5Cright)%2BX%5E%7B(l)%7D%0A%5Ctag%7B8%7D%0A#card=math&code=X%5E%7B%28l%2B1%29%7D%3D%5Csigma%5Cleft%28A%5E%7B%5Cprime%7D%20X%5E%7B%28l%29%7D%20W%5E%7B%28l%29%7D%5Cright%29%2BX%5E%7B%28l%29%7D%0A%5Ctag%7B8%7D%0A&id=wKsW9)

在这里，我们提出了另一种简单的技术来改善深层GCN神经网络的训练。在原始的GCN的设置里，每个节点都聚合邻接节点在上一层的表征。然而，在深层GCN的设置里，该策略可能不适合，因为它没有考虑到层数的问题。直观地说，近距离的邻接节点应该比远距离的的邻接节点贡献更大。因此，Cluster-GCN提出一种技术来更好地解决这个问题。其主要思想是放大GCN每一层中使用的邻接矩阵的对角线部分。通过这种方式，我们在GCN的每一层的聚合中对来自上一层的表征赋予更大的权重。这可以通过给加上一个单位矩阵来实现，公式如下，

%7D%3D%5Csigma%5Cleft(%5Cleft(A%5E%7B%5Cprime%7D%2BI%5Cright)%20X%5E%7B(l)%7D%20W%5E%7B(l)%7D%5Cright)%0A%5Ctag%7B9%7D%0A#card=math&code=X%5E%7B%28l%2B1%29%7D%3D%5Csigma%5Cleft%28%5Cleft%28A%5E%7B%5Cprime%7D%2BI%5Cright%29%20X%5E%7B%28l%29%7D%20W%5E%7B%28l%29%7D%5Cright%29%0A%5Ctag%7B9%7D%0A&id=qfxij)

虽然公式(9)似乎是合理的，但对所有节点使用相同的权重而不考虑其邻居的数量可能不合适。此外，它可能会受到数值不稳定的影响，因为当使用更多的层时，数值会呈指数级增长。因此，Cluster-GCN方法提出了一个修改版的公式(9)，以更好地保持邻接节点信息和数值范围。首先给原始的添加一个单位矩阵，并进行归一化处理

%5E%7B-1%7D(A%2BI)%0A%5Ctag%7B10%7D%0A#card=math&code=%5Ctilde%7BA%7D%3D%28D%2BI%29%5E%7B-1%7D%28A%2BI%29%0A%5Ctag%7B10%7D%0A&id=q3h9h)

然后考虑，

%7D%3D%5Csigma%5Cleft((%5Ctilde%7BA%7D%2B%5Clambda%20%5Coperatorname%7Bdiag%7D(%5Ctilde%7BA%7D))%20X%5E%7B(l)%7D%20W%5E%7B(l)%7D%5Cright)%0A%5Ctag%7B11%7D%0A#card=math&code=X%5E%7B%28l%2B1%29%7D%3D%5Csigma%5Cleft%28%28%5Ctilde%7BA%7D%2B%5Clambda%20%5Coperatorname%7Bdiag%7D%28%5Ctilde%7BA%7D%29%29%20X%5E%7B%28l%29%7D%20W%5E%7B%28l%29%7D%5Cright%29%0A%5Ctag%7B11%7D%0A&id=G8ezl)

3. 代码实现

3.1 数据集分析

from torch_geometric.datasets import Reddit
from torch_geometric.data import ClusterData, ClusterLoader, NeighborSampler
dataset = Reddit('D://Dataset/Reddit')
data = dataset[0]
print(f'Number of classes: {dataset.num_classes}')
print(f'Number of nodes: {data.num_nodes}')
print(f'Number of edges: {data.num_edges}')
print(f'Number of features: {data.num_features}')
'''
Downloading https://data.dgl.ai/dataset/reddit.zip
Extracting D:\Dataset\Reddit\raw\reddit.zip
Processing...
Done!
Number of classes: 41
Number of nodes: 232965
Number of edges: 114615892
Number of features: 602
'''

可以看到该数据集包含41类标签，232,965个节点，114,615,873条边，节点维度为602维。

3.2 图节点聚类与数据加载器生成

cluster_data = ClusterData(data, num_parts=1500, recursive=False, save_dir=dataset.processed_dir)
train_loader = ClusterLoader(cluster_data, batch_size=20, shuffle=True, num_workers=12)
subgraph_loader = NeighborSampler(data.edge_index, sizes=[-1], batch_size=1024, shuffle=False, num_workers=12)

• ClusterData(data , num_parts : int, recursive : bool= False, save_dir : Optional str = None , log : bool= True)
  • 作用：将图数据对象聚类/划分为多个子图
  • 参数说明：
    • num_parts：分区数
    • recrusive：如果设置为True，将使用多级递归二分法而不是多级 k 路分区
    • save_dir：如果设置，会将分区数据保存到save_dir目录中便于复用。
    • log：如果设置为False，则不会记录任何进度。

• ClusterLoader(cluster_data , **kwargs):
  • 作用：将来自大规模图数据对象的分区子图及其子图间的边合并成一个小批量。
  • 参数说明：
    • cluster_data：已经分区的数据对象。
    • **kwargs：torch.utils.data.DataLoader的附加参数，例如batch_size, shuffle, drop_last或num_workers。

• NeighborSampler(edge_index: Union[torch.Tensor, torch_sparse.tensor.SparseTensor], sizes: List[int], node_idx: Optional[torch.Tensor] = None, num_nodes: Optional[int] = None, return_e_id: bool = True, transform: Optional[Callable] = None, **kwargs):
  • 作用：在无法进行全批量训练的大规模图上对 GNN 进行小批量训练。
    给定一个层的GNN和我们想要计算表征的特定小批量节点node_idx，该模块迭代地采样邻居并构建模拟 GNN 实际计算流程的二分图。
    更具体地说，sizes表示我们想要为每一层中的每个节点采样多少邻居。然后，该模块接收sizes，并且sizes[l]为 第l层中每个节点采样的邻居数。在下一层中，对已经遇到的节点的联合重复采样。然后以反向模式返回实际的计算图，这意味着我们将消息从一组较大的节点传递到一组较小的节点，直到到达我们最初想要计算表征的节点。
    因此，由NeighborSampler返回的项包含当前的batch_size 、参与计算的所有节点的IDn_id以及通过 tuple(edge_index, e_id, size) 的二分图对象列表，其中edge_index表示源节点和目标节点之间的二部边，e_id表示在大规模图中的原始边的ID。size表示二部图的形状。对于每个二分图，目标节点也包含在源节点列表的开头，以便人们可以轻松地应用跳过连接或添加自循环。
  • 参数说明：
    • edge_index(Tensor或SparseTensor)：
      • 定义底层图形连接/消息传递流，类型是torch.LongTensor或 torch_sparse.SparseTensor。 edge_index保存（稀疏）对称邻接矩阵的索引。
      • 如果edge_index是torch.LongTensor类型，则其形状必须定义为[2, num_edges]，如果flow=“source_to_target，则消息从edge_index[0]的节点传播到edge_index[1]中的对应节点。
      • 如果edge_index是torch_sparse.SparseTensor类型，则其稀疏索引(row, col)应与row=edge_index[1]和col=edge_index[0]相关。
      • 两种格式的主要区别在于我们是否输入转置的稀疏邻接矩阵。

  - `size`：为每一层中的每个节点采样的邻居数。如果设置`sizes[l]`为`-1`，则所有邻居都包含在`l`层中。
  - `node_idx(LongTensor, optional)`：创建小批量时应考虑的节点。如果设置为`[None](https://docs.python.org/3/library/constants.html#None)`，将考虑所有节点。
  - `num_nodes` ：图中节点的数量（默认值：`[None](https://docs.python.org/3/library/constants.html#None)`）。
  - `return_e_id(bool)` ：如果设置为`[False](https://docs.python.org/3/library/constants.html#False)`，则不会返回采样边的原始边索引。这仅在对没有边缘特征的图形进行操作以节省内存的情况下才有用（默认值：`[True](https://docs.python.org/3/library/constants.html#True)`）。
  - `transform (callable, optional)`：一个函数/转换，它接受一个采样的小批量并返回一个转换后的版本（默认值：`[None](https://docs.python.org/3/library/constants.html#None)`）。
  - `**kwargs(optional)`：`torch.utils.data.DataLoader`的附加参数，例如`batch_size`,  `shuffle`, `drop_last`或`num_workers`。

【注意】：这里内存不够的话会报错。

【补充】：num_workers的作用

1. 每个epoch的dataloader加载数据时，dataloader一次性创建num_workers个worker（也可以说dataloader一次性创建num_worker个工作进程，worker也是普通的工作进程），并用batch_sampler将指定batch分配给指定worker，worker将它负责的batch加载进RAM。然后，dataloader从RAM中找本轮迭代要用的batch，如果找到了，就使用。如果没找到，就要num_worker个worker继续加载batch到内存，直到dataloader在RAM中找到目标batch。一般情况下都是能找到的，因为batch_sampler指定batch时当然优先指定本轮要用的batch。
2. num_worker设置得大，好处是寻batch速度快，因为下一轮迭代的batch很可能在上一轮/上上一轮…迭代时已经加载好了。坏处是内存开销大，也加重了CPU负担（worker加载数据到RAM的进程是CPU复制的嘛）。num_workers的经验设置值是自己电脑/服务器的CPU核心数，如果CPU很强、RAM也很充足，就可以设置得更大些。
3. 如果num_worker设为0，意味着每一轮迭代时，dataloader不再有自主加载数据到RAM这一步骤（因为没有worker了），而是在RAM中找batch，找不到时再加载相应的batch。缺点当然是速度更慢。

3.3 图神经网络的构建

import torch
import torch.nn.functional as F
from torch.nn import ModuleList
from tqdm import tqdm
from torch_geometric.nn import SAGEConv

class Net(torch.nn.Module):
    def __init__(self, in_channels, out_channels):
        super(Net, self).__init__()
        self.convs = ModuleList(
            [SAGEConv(in_channels, 128),
             SAGEConv(128, out_channels)])

    def forward(self, x, edge_index):
        for i, conv in enumerate(self.convs):
            x = conv(x, edge_index)
            if i != len(self.convs) - 1:
                x = F.relu(x)
                x = F.dropout(x, p=0.5, training=self.training)
        return F.log_softmax(x, dim=-1)

    def inference(self, x_all，device):
        # 显示进度条
        pbar = tqdm(total=x_all.size(0) * len(self.convs))
        pbar.set_description('Evaluating')

        '''
        Compute representations of nodes layer by layer, using *all*
        available edges. This leads to faster computation in contrast to
        immediately computing the final representations of each batch.
        '''

        for i, conv in enumerate(self.convs):
            xs = []
            for batch_size, n_id, adj in subgraph_loader:
                edge_index, _, size = adj.to(device)
                x = x_all[n_id].to(device)
                x_target = x[:size[1]]
                x = conv((x, x_target), edge_index)
                if i != len(self.convs) -1:
                    x = F.relu(x)
                xs.append(x.cpu())

                pbar.update(batch_size)

            x_all = torch.cat(xs, dim=0)

        pbar.close()

        return x_all

【注意】：如果内存不够的话这里会报错

• inference()：应用于推理阶段，为了获取更高的预测精度，所以使用subgraph_loader

3.4 训练、测试和验证

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Net(dataset.num_features, dataset.num_classes).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.005)

def train():
    model.train()

    total_loss = total_nodes = 0
    for batch in train_loader:
        batch = batch.to(device)
        optimizer.zero_grad()
        out = model(batch.x, batch.edge_index)
        loss = F.nll_loss(out[batch.train_mask], batch.y[batch.train_mask])
        loss.backward()
        optimizer.step()

        nodes = batch.train_mask.sum().item()
        total_loss += loss.item()*nodes
        total_nodes += nodes

    return total_loss / total_nodes

@torch.no_grad()
def test():
    # Inference should be performed on the full graph.
    model.eval()

    out = model.inference(data.x, device)
    y_pred = out.argmax(dim=-1)

    accs = []
    for mask in [data.train_mask, data.val_mask, data.test_mask]:
        correct = y_pred[mask].eq(data.y[mask]).sum().item()
        accs.append(correct / mask.sum().item())
    return accs

for epoch in range(1, 31):
    loss = train()
    if epoch % 5 == 0:
        train_acc, val_acc, test_acc = test()
        print(f'Epoch: {epoch:02d}, Loss: {loss:.4f}, Train: {train_acc:.4f}, '
              f'Val: {val_acc:.4f}, test: {test_acc:.4f}')
    else:
        print(f'Epoch: {epoch:02d}, Loss: {loss:.4f}')

在训练过程中，我们使用train_loader获取batch，每次根据多个簇组成的batch进行神经网络的训练。但在验证阶段，我们使用subgraph_loader，在计算一个节点的表征时会计算该节点的距离从到的邻接节点，这么做可以更好地测试神经网络的性能。

结果如下：

【注意】：如果内存不够大的话这里同样也会报错，可以通过增加虚拟内存解决该问题，具体步骤如下：

• 查看高级系统设置 - 高级 - 性能 - 高级 - 虚拟内存
  
• 修改虚拟内存，这里我选择了增加D盘的虚拟内存
  

4. 实验部分

文中通过与GraphSAGE和VRGCN在四个数据集(Reddit(128), Reddit( 512), Amazon(128), PPI(512))上进行实验来验证Cluster-GCN的性能。这里我选择在PPI数据集上对比Cluster-GCN和GraphSAGE的性能进行实验，模型全部基于PyG框架实现。

4.1 在中型数据集上的训练表现

4.1.1 训练时间与准确度

下图展示了这几个模型的训练时间和准确度（F1-Score）的差别，其中x轴表示以秒为单位的训练时间，y轴表示准确度

这里我进行了GraphSAGE和Cluster-GCN在PPI数据集上的训练时间和准确度的对比

4.1.1.1 数据集分析

dataset = PPI('D://Dataset/PPI')
data = dataset[0]

print(f'Number of graphs: {len(dataset)}')
print(f'Number of classes: {dataset.num_classes}')
print(f'Number of nodes: {data.num_nodes}')
print(f'Number of edges: {data.num_edges}')
print(f'Number of features: {data.num_features}')

'''
Downloading https://data.dgl.ai/dataset/ppi.zip
Extracting D:\Dataset\PPI\ppi.zip
Processing...
Done!

Number of graphs: 20
Number of classes: 121
Number of nodes: 1767
Number of edges: 32318
Number of features: 50
'''

可以看出，PyG库中的PPI数据集有20个图，且第一个图中有1,767个节点，32,318条边。

4.1.1.2 GraphSAGE on PPI

（这里我还在把PyG库中example中的非监督GraphSAGE改成监督模型，后面补）

4.1.1.3 Cluster-GCN on PPI

import torch
import torch.nn.functional as F
from torch_geometric.datasets import PPI
from torch_geometric.nn import SAGEConv, BatchNorm
from torch_geometric.data import Batch, ClusterData, ClusterLoader, DataLoader
from sklearn.metrics import f1_score

train_dataset = PPI('D://Dataset/PPI', split='train')
val_dataset = PPI('D://Dataset/PPI', split='val')
test_dataset = PPI('D://Dataset/PPI', split='test')

train_data = Batch.from_data_list(train_dataset)
cluster_data = ClusterData(train_data, num_parts=50, recursive=False,save_dir=train_dataset.processed_dir)

# train_loader = ClusterLoader(cluster_data, batch_size=1, shuffle=True, num_workers=12)
# 这里我的num_workers设置为0，否则会报错
train_loader = ClusterLoader(cluster_data, batch_size=1, shuffle=True)

val_loader = DataLoader(val_dataset, batch_size=2, shuffle=False)
test_loader = DataLoader(test_dataset, batch_size=2, shuffle=False)


class Net(torch.nn.Module):
    def __init__(self, in_channels, hidden_channels, out_channels, num_layers):
        super(Net, self).__init__()
        self.convs = torch.nn.ModuleList()
        self.batch_norms = torch.nn.ModuleList()
        self.convs.append(SAGEConv(in_channels, hidden_channels))
        self.batch_norms.append(BatchNorm(hidden_channels))
        for _ in range(num_layers - 2):
            self.convs.append(SAGEConv(hidden_channels, hidden_channels))
            self.batch_norms.append(BatchNorm(hidden_channels))
        self.convs.append(SAGEConv(hidden_channels, out_channels))

    def forward(self, x, edge_index):
        for conv, batch_norm in zip(self.convs[:-1], self.batch_norms):
            x = conv(x, edge_index)
            x = batch_norm(x)
            x = F.relu(x)
            x = F.dropout(x, p=0.2, training=self.training)
        return self.convs[-1](x, edge_index)


device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Net(in_channels=train_dataset.num_features, hidden_channels=1024,
            out_channels=train_dataset.num_classes, num_layers=6).to(device)
loss_op = torch.nn.BCEWithLogitsLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)


def train():
    model.train()

    total_loss = 0
    for data in train_loader:
        data = data.to(device)
        optimizer.zero_grad()
        loss = loss_op(model(data.x, data.edge_index), data.y)
        loss.backward()
        optimizer.step()
        total_loss += loss.item() * data.num_nodes
    return total_loss / train_data.num_nodes


@torch.no_grad()
def test(loader):
    model.eval()

    ys, preds = [], []
    for data in loader:
        ys.append(data.y)
        out = model(data.x.to(device), data.edge_index.to(device))
        preds.append((out > 0).float().cpu())

    y, pred = torch.cat(ys, dim=0).numpy(), torch.cat(preds, dim=0).numpy()
    # 这里同样也采用f1_score
    return f1_score(y, pred, average='micro') if pred.sum() > 0 else 0


for epoch in range(1, 201):
    loss = train()
    val_f1 = test(val_loader)
    test_f1 = test(test_loader)
    print('Epoch: {:02d}, Loss: {:.4f}, Val: {:.4f}, Test: {:.4f}'.format(
        epoch, loss, val_f1, test_f1))

结果如下图所示（中间的结果省略）：

【复习】：

• BatchNorm的作用：

深度神经网络的目标就是通过学习训练数据的分布，并在测试集上达到很好的泛化效果，但是，如果我们每一个batch输入的数据都具有不同的分布，显然会给网络的训练带来困难。另一方面，数据经过一层层网络计算后，其数据分布也在发生着变化，此现象称为内部协变量偏移（Internal Covariate Shift），会给下一层的网络学习带来困难。因此，深度学习需要对数据做归一化。

归一化的公式如下：

4.2 训练更深层的GCN

文中在PPI数据集上测试更深层的GCN的表现会不会更好，结果如下表所示

这里(9)、(10)、(11)表示使用不同的更新函数，对应2.2.4节的三个更新函数。可以看到，对于2至5层的情况，所有方法的准确性随着更多的层增加而增加，表明更深的GCN可能是有用的。然而，当使用7至8层GCN时，前三种方法无法在200 epoch内收敛，并且准确性也明显下降。

我这里对4层和6层的GCN在Reddit数据集上进行实验，隐藏层单元数均为128。

4.2.1 四层GCN

import torch
import torch.nn.functional as F
from torch.nn import ModuleList
from tqdm import tqdm
from torch_geometric.nn import SAGEConv
from torch_geometric.datasets import Reddit
from torch_geometric.data import ClusterData, ClusterLoader, NeighborSampler

class Net(torch.nn.Module):

    def __init__(self, in_channels, out_channels):
        super(Net, self).__init__()
        self.convs = ModuleList(
            [SAGEConv(in_channels, 128),
             SAGEConv(128, 128),
             SAGEConv(128, 128),
             SAGEConv(128, out_channels)]
        )

    def forward(self, x, edge_index):
        for i, conv in enumerate(self.convs):
            x = conv(x, edge_index)
            if i != len(self.convs) - 1:
                x = F.relu(x)
                x = F.dropout(x, p=0.5, training=self.training)
        return F.log_softmax(x, dim=-1)

    def inference(self, x_all, device, subgraphLoader):
        # 显示进度条
        pbar = tqdm(total=x_all.size(0)*len(self.convs))
        pbar.set_description('Evaluating')

        '''
            Compute representations of nodes layer by layer, using *all*
            available edges. This leads to faster computation in contrast to
            immediately computing the final representations of each batch.
        '''

        for i, conv in enumerate(self.convs):
            xs = []
            for batch_size, n_id, adj in subgraphLoader:
                edge_index, _, size = adj.to(device)
                x = x_all[n_id].to(device)
                x_target = x[:size[1]]
                x = conv((x, x_target), edge_index)
                if i != len(self.convs) - 1:
                    x = F.relu(x)
                xs.append(x.cpu())

                pbar.update(batch_size)

            x_all = torch.cat(xs, dim=0)

        pbar.close()

        return x_all


def train(model, trainLoader, optimizer, device):
    model.train()

    total_loss = total_nodes = 0
    for batch in trainLoader:
        batch = batch.to(device)
        optimizer.zero_grad()
        out = model(batch.x, batch.edge_index)
        loss = F.nll_loss(out[batch.train_mask], batch.y[batch.train_mask])
        loss.backward()
        optimizer.step()

        nodes = batch.train_mask.sum().item()
        total_loss += loss.item()*nodes
        total_nodes += nodes

    return total_loss/total_nodes



@torch.no_grad()
def test(model, data, device, subgraphLoader):
    # 在全图上进行推理
    model.eval()

    out = model.inference(data.x, device, subgraphLoader)
    y_pred = out.argmax(dim=-1)

    accs = []
    for mask in [data.train_mask, data.val_mask, data.test_mask]:
        correct = y_pred[mask].eq(data.y[mask]).sum().item()
        accs.append(correct / mask.sum().item())
    return accs


def main():

    dataset = Reddit('D://Dataset/Reddit')
    data = dataset[0]

    # 将图数据划分为1500个子图
    clusterData = ClusterData(data, num_parts=1500, recursive=False, save_dir=dataset.processed_dir)
    # 将1000个分区子图及其之间的边合并成20个小批量 
    trainLoader = ClusterLoader(clusterData, batch_size=20, shuffle=True, num_workers=12)
    # 对邻居节点进行采样，这里size=[-1]表示全采样
    subgraphLoader = NeighborSampler(data.edge_index, sizes=[-1], batch_size=512, num_workers=12)

    device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
    model = Net(dataset.num_features, dataset.num_classes).to(device)
    optimizer = torch.optim.Adam(model.parameters(), lr=0.005)

    for epoch in range(1, 31):
        loss = train(model, trainLoader, optimizer, device)
        if epoch % 5 == 0:
            train_acc, val_acc, test_acc = test(model, data, device, subgraphLoader)
            print(f'Epoch: {epoch:02d}, Loss: {loss:.4f}, Train: {train_acc:.4f}, '
                  f'Val: {val_acc:.4f}, test: {test_acc:.4f}')
        else:
            print(f'Epoch: {epoch:02d}, Loss: {loss:.4f}')


if __name__ == "__main__":
    main()

结果如下图所示：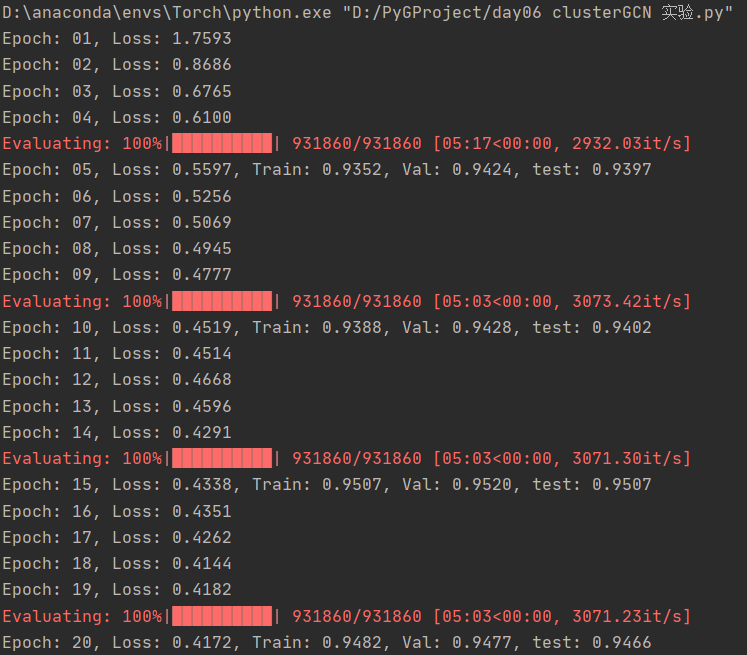

可以看到，四层的效果就已经不如两层了，这里可能有两个原因

• 一是我的模型有问题，因为只简单增加了两层GraphSAGE
• 二是原文中使用的是`PPI数据集，而我使用的是Reddit数据集

5. 总结

本文提出的Cluster-GCN采用了一种全新的训练方法，它使大规模图在GCN上的训练的难度大大下降。他不像GraphSAGE通过采样的方式聚集邻居节点信息，而是先以最大化簇内边的方式将图划分为子图，然后将不同的子图及其之间的边组成一个batch，相比采样，这种方式损失的信息更少（由子图组合的batch考虑了图内边）。

6. 作业

• 尝试将数据集切分成不同数量的簇进行实验，然后观察结果并进行比较。

这里我选择将簇的数量减少为1000来进行实验，代码如下：

import torch
import torch.nn.functional as F
from torch.nn import ModuleList
from tqdm import tqdm
from torch_geometric.nn import SAGEConv
from torch_geometric.datasets import Reddit
from torch_geometric.data import ClusterData, ClusterLoader, NeighborSampler

class Net(torch.nn.Module):

    def __init__(self, in_channels, out_channels):
        super(Net, self).__init__()
        self.convs = ModuleList(
            [SAGEConv(in_channels, 128),
             SAGEConv(128, out_channels)]
        )

    def forward(self, x, edge_index):
        for i, conv in enumerate(self.convs):
            x = conv(x, edge_index)
            if i != len(self.convs) - 1:
                x = F.relu(x)
                x = F.dropout(x, p=0.5, training=self.training)
        return F.log_softmax(x, dim=-1)

    def inference(self, x_all, device, subgraphLoader):
        # 显示进度条
        pbar = tqdm(total=x_all.size(0)*len(self.convs))
        pbar.set_description('Evaluating')

        '''
            Compute representations of nodes layer by layer, using *all*
            available edges. This leads to faster computation in contrast to
            immediately computing the final representations of each batch.
        '''

        for i, conv in enumerate(self.convs):
            xs = []
            for batch_size, n_id, adj in subgraphLoader:
                edge_index, _, size = adj.to(device)
                x = x_all[n_id].to(device)
                x_target = x[:size[1]]
                x = conv((x, x_target), edge_index)
                if i != len(self.convs) - 1:
                    x = F.relu(x)
                xs.append(x.cpu())

                pbar.update(batch_size)

            x_all = torch.cat(xs, dim=0)

        pbar.close()

        return x_all


def train(model, trainLoader, optimizer, device):
    model.train()

    total_loss = total_nodes = 0
    for batch in trainLoader:
        batch = batch.to(device)
        optimizer.zero_grad()
        out = model(batch.x, batch.edge_index)
        loss = F.nll_loss(out[batch.train_mask], batch.y[batch.train_mask])
        loss.backward()
        optimizer.step()

        nodes = batch.train_mask.sum().item()
        total_loss += loss.item()*nodes
        total_nodes += nodes

    return total_loss/total_nodes



@torch.no_grad()
def test(model, data, device, subgraphLoader):
    # 在全图上进行推理
    model.eval()

    out = model.inference(data.x, device, subgraphLoader)
    y_pred = out.argmax(dim=-1)

    accs = []
    for mask in [data.train_mask, data.val_mask, data.test_mask]:
        correct = y_pred[mask].eq(data.y[mask]).sum().item()
        accs.append(correct / mask.sum().item())
    return accs


def main():

    dataset = Reddit('D://Dataset/Reddit')
    data = dataset[0]

    # 将图数据划分为1000个子图
    clusterData = ClusterData(data, num_parts=1000, recursive=False, save_dir=dataset.processed_dir)
    # 将1000个分区子图及其之间的边合并成20个小批量
    trainLoader = ClusterLoader(clusterData, batch_size=20, shuffle=True, num_workers=12)
    # 对邻居节点进行采样，这里size=[-1]表示全采样
    subgraphLoader = NeighborSampler(data.edge_index, sizes=[-1], batch_size=1024, num_workers=12)

    device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
    model = Net(dataset.num_features, dataset.num_classes).to(device)
    optimizer = torch.optim.Adam(model.parameters(), lr=0.005)

    for epoch in range(1, 31):
        loss = train(model, trainLoader, optimizer, device)
        if epoch % 5 == 0:
            train_acc, val_acc, test_acc = test(model, data, device, subgraphLoader)
            print(f'Epoch: {epoch:02d}, Loss: {loss:.4f}, Train: {train_acc:.4f}, '
                  f'Val: {val_acc:.4f}, test: {test_acc:.4f}')
        else:
            print(f'Epoch: {epoch:02d}, Loss: {loss:.4f}')


if __name__ == "__main__":
    main()

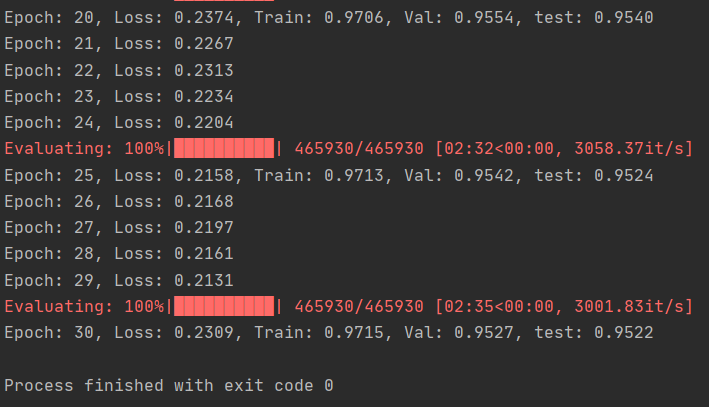
结果如下图所示，和1500个簇差不多

7. 参考资料

• DataWhale开源学习资料：https://github.com/datawhalechina/team-learning-nlp/tree/master/GNN
• PyG官方文档：https://pytorch-geometric.readthedocs.io/en/latest/modules/data.html?highlight=NeighborSampler()%3A#torch_geometric.data.NeighborSampler%3A#torch_geometric.data.NeighborSampler)
• Github：https://github.com/rusty1s/pytorch_geometric/tree/master/examples
• CSDN：https://blog.csdn.net/weixin_43593330/article/details/107483671
• 知乎专栏：https://zhuanlan.zhihu.com/p/168791054
• Cluster-GCN论文：https://arxiv.org/abs/1905.07953