引言

图表征学习要求根据节点属性、边和边的属性（如果有的话）生成一个向量作为图的表征，这个表征可以用做图的预测。本文中我们将以图同构网络（Graph Isomorphism Network, GIN）为例介绍基于图神经网络的图表征学习方法。

1. 产生背景

1.1 基本概念

• 可重复集合（Multiset）：
  可重复集合是一个广义的集合概念，它允许有重复的元素。 一个节点的所有邻接节点是一个可重复集合，一个节点可以有重复的邻接节点，邻接节点没有顺序关系。
• 单射（injectivity）：
  如果函数将不同的元素映射到不同的输出，则该函数是单射的，如下图例子所示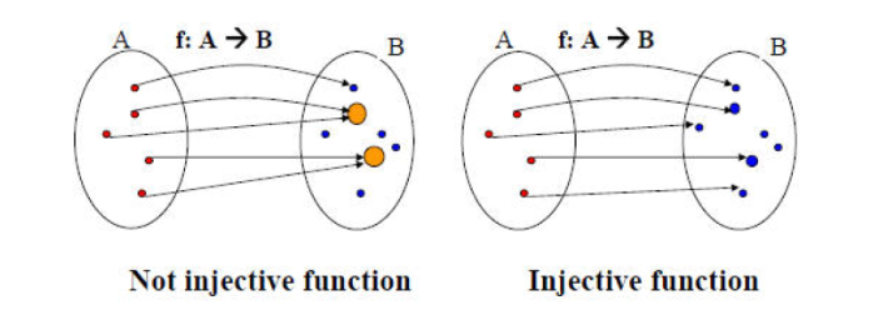
  

1.2 为什么基于mean、max aggregate的GNN表征能力不够强大

1.2.1 sum、mean 和 max 分别可以捕获哪些信息

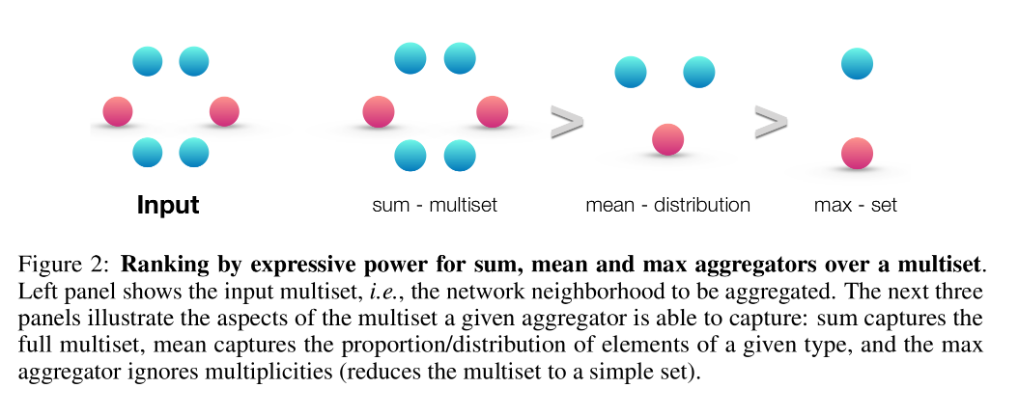
三种不同的聚合方式的区别如下：

• sum：学习全部的标签以及数量，可以学习精确的结构信息；
• mean：学习标签的比例（比如两个图标签比例相同，但是节点有倍数关系），偏向学习分布信息；
• max：学习最大标签，忽略多样性，偏向学习有代表性的元素信息。

选择聚合方式的优先级为：

• sum > mean > max

1.2.2 mean 和 max 无法区分哪些结构

节点和为中心节点，通过聚合邻居特征生成表征向量，分析设置不同的聚合方式是否能区分不同的结构（如果能捕获不同结构，二者的表征向量应该不一样）。

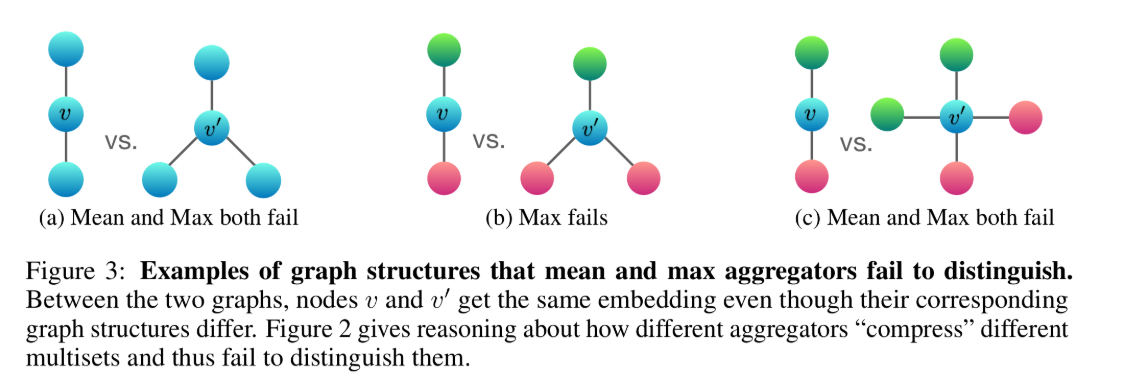
这里假设红色、蓝色和绿色节点的特征值为r、g、b，只考虑聚合方式：

• 图(a)
  | 聚合方式 | 左图 | 右图 | 结论 | | —- | —- | —- | —- | | sum | b+b = 2b | b+b+b = 3b | 可以区分 | | mean | (b+b)/2 = b | (b+b+b)/3 = b | 不可以区分 | | max | b | b | 不可以区分 |

• 图(b)
  | 聚合方式 | 左图 | 右图 | 结论 | | —- | —- | —- | —- | | sum | r+g | 2r+g | 可以区分 | | mean | (r+g)/2 | (2r+g)/3 | 可以区分 | | max | max(g, r) | max(g, r, r) | 不可以区分 |

• 图(c)
  | 聚合方式 | 左图 | 右图 | 结论 | | —- | —- | —- | —- | | sum | r+g | 2r+2g | 可以区分 | | mean | (r+g)/2 | (2r+2g)/4 = (r+g)/2 | 不可以区分 | | max | max(g, r) | max(g, g, r, r) | 不可以区分 |

【结论】：由于 mean 和 max-pooling 函数不满足单射性，无法区分某些结构的图，故性能会比 sum 差一点。

1.3 GNN 与 Weisfeiler-Lehman Test

新的图神经网络的设计大多基于经验性的直觉、启发式的方法和实验性的试错。人们对图神经网络的特性和局限性了解甚少，对图神经网络的表征能力学习的正式分析也很有限。因此，本文就提出了通过结合 Weisfeiler-Lehman Test 来评价图神经网络的表征能力。

1.3.1 符号定义

• 图：#card=math&code=G%3D%28V%2C%20E%29&id=V3fau)，其中是图的节点集
• 度矩阵：#card=math&code=D%20%3D%20diag%28d1%2C%20…%2C%20d_n%29&id=zZ6Dd)，其中
• 图的集合：
• 维节点的预测标签：
• 节点的表征向量：
• 要学习的节点的表征向量：
• 节点的预测标签：#card=math&code=y_v%3Df%28h_v%29&id=riI8L)
• 图G的表征向量：
• 图G的预测标签：#card=math&code=y_G%20%3D%20h%28h_G%29&id=SMXf9)

1.3.2 图神经网络回顾

图神经网络的目标是以图结构数据和节点特征作为输入，以学习到节点（或图）的表示，用于分类任务。基于消息传播的图神经网络可以分为如下三个模块：

• 聚合（Aggregate）：聚合一阶邻居节点的信息
• 更新（Combine）：将邻居聚合的特征与当前节点特征合并，以更新当前节点特征。
• 读出（Readout）：如果是对图进行分类，需要将图中中所有节点特征转变成图的特征，这个过程称为读出。

目前的GNNs都遵循一个邻居聚合的策略，也就是通过聚合邻居的表示然后迭代地更新自己的表示。在k次迭代聚合后就可以捕获到在k-hop邻居内的结构信息。一个k层的GNNs可以表示为：

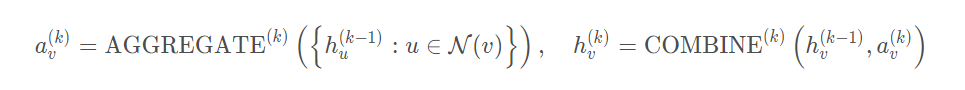
可以看出聚合和更新是图神经网络中两个最重要的部分。下面来看两个例子：

• GraphSAGE：
  • 聚合函数： %7D%20%3D%20MAX(%5C%7BReLU(W%C2%B7h_u%5E%7B(k-1)%7D)%2C%20%5Cforall%20u%20%5Cin%20%5Cmathcal%7BN%7D(v)%20%5C%7D)%0A#card=math&code=a_v%5E%7B%28k%29%7D%20%3D%20MAX%28%5C%7BReLU%28W%C2%B7h_u%5E%7B%28k-1%29%7D%29%2C%20%5Cforall%20u%20%5Cin%20%5Cmathcal%7BN%7D%28v%29%20%5C%7D%29%0A&id=OeRix)
  • 更新函数： %7D%20%3D%20W%C2%B7%5Ba_v%5E%7B(k)%7D%2C%20h_v%5E%7B(k-1)%7D%5D%0A#card=math&code=h_v%5E%7B%28k%29%7D%20%3D%20W%C2%B7%5Ba_v%5E%7B%28k%29%7D%2C%20h_v%5E%7B%28k-1%29%7D%5D%0A&id=Q2gyd)
    其中W是可学习的参数矩阵。

• GCN：
  • 聚合函数：平均池化
  • 更新函数：加权的ReLU

整合到一起得到公式： %7D%20%3D%20ReLU(W%C2%B7MEAN%5C%7Bh_u%5E%7B(k-1)%7D%2C%20%5Cforall%20u%20%5Cin%20%5Cmathcal%7BN%7D(v)%20%5Ccup%20%5C%7Bv%5C%7D%5C%7D)%0A#card=math&code=h_v%5E%7B%28k%29%7D%20%3D%20ReLU%28W%C2%B7MEAN%5C%7Bh_u%5E%7B%28k-1%29%7D%2C%20%5Cforall%20u%20%5Cin%20%5Cmathcal%7BN%7D%28v%29%20%5Ccup%20%5C%7Bv%5C%7D%5C%7D%29%0A&id=YWzZT)

1.3.3 节点分类与图分类

• 节点分类任务：节点在最后一层的表示%7D#card=math&code=h_v%5E%7B%28K%29%7D&id=VmuUE)就可以用于预测
• 图分类任务：需要将图中中所有节点特征转变成图的特征，即整个图的表征，这里需要用到读出函数，公式如下： %7D%7Cv%20%5Cin%20G%7D)%0A#card=math&code=h_G%20%3D%20READOUT%28%7Bh_v%5E%7B%28K%29%7D%7Cv%20%5Cin%20G%7D%29%0A&id=sXIW7)
  READOUT表示一个置换不变性函数（permutation invariant function），也可以是一个图级别的池化函数。

1.3.4 Weisfeiler-Lehman 图同构性测试（Weisfeiler-Lehman Test，WL Test）

1.3.4.1 图同构性测试

在学习图同构性测试之前，先来介绍一下同构图的定义，

• 两个图是同构的，意思是两个图拥有一样的拓扑结构，也就是说，我们可以通过重新标记节点从一个图转换到另外一个图。

Weisfeiler-Lehman 图的同构性测试算法，简称WL Test，是一种用于测试两个图是否同构的算法。

WL Test 的一维形式，类似于图神经网络中的邻接节点聚合。WL Test 首先迭代地聚合节点及其邻接节点的标签，然后将聚合的标签散列（hash）成新标签，该过程形式化为下方的公式，

%7D%20L%5E%7Bh-1%7D%7Bv%7D%5Cright)%0A#card=math&code=L%5E%7Bh%7D%7Bu%7D%20%5Cleftarrow%20%5Coperatorname%7Bhash%7D%5Cleft%28L%5E%7Bh-1%7D%7Bu%7D%20%2B%20%5Csum%7Bv%20%5Cin%20%5Cmathcal%7BN%7D%28U%29%7D%20L%5E%7Bh-1%7D_%7Bv%7D%5Cright%29%0A&id=i2H3v)

在上方的公式中，表示节点的第次迭代的标签，第次迭代的标签为节点原始标签。

在迭代过程中，发现两个图之间的节点的标签不同时，就可以确定这两个图是非同构的。需要注意的是节点标签可能的取值只能是有限个数。

【注意】：WL Test 不能保证对所有图都有效，特别是对于具有高度对称性的图，如链式图、完全图、环图和星图，它会判断错误。

Weisfeiler-Lehman Graph Kernels 方法提出用WL子树核衡量图之间相似性。该方法使用WL Test不同迭代中的节点标签计数作为图的表征向量，它具有与WL Test相同的判别能力。直观地说，在WL Test的第次迭代中，一个节点的标签代表了以该节点为根的高度为的子树结构。

下面结合一个例子说明，给定两个图和，每个节点拥有标签（实际中，一些图没有节点标签，我们可以以节点的度作为标签）。

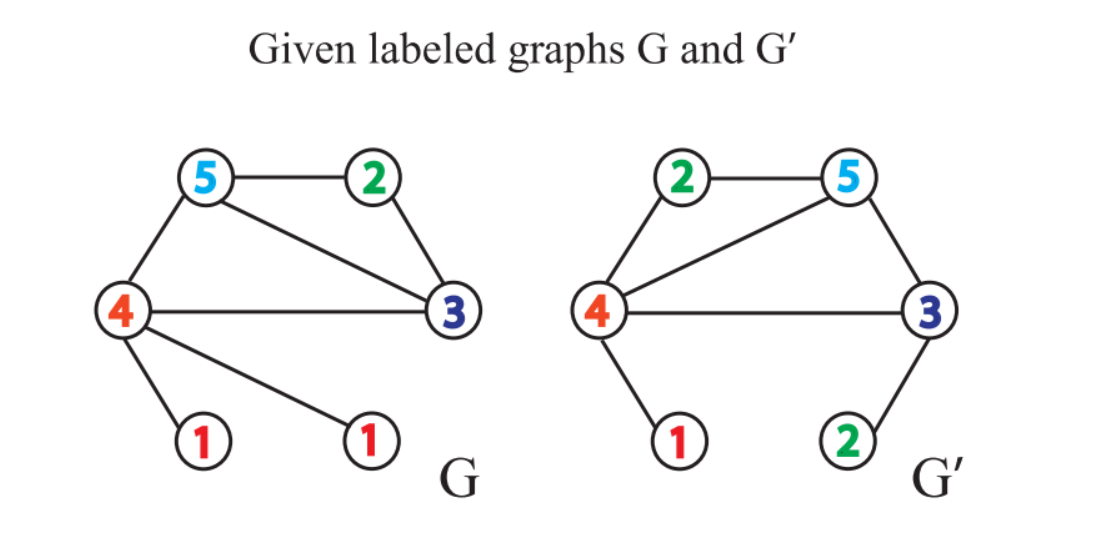
Weisfeiler-Leman Test 算法通过重复执行以下给节点打标签的过程来实现图是否同构的判断：

1. 聚合自身与邻接节点的标签得到一串字符串，自身标签与邻接节点的标签中间用,分隔，邻接节点的标签按升序排序。排序的原因在于要保证单射性，即保证输出的结果不因邻接节点的顺序改变而改变。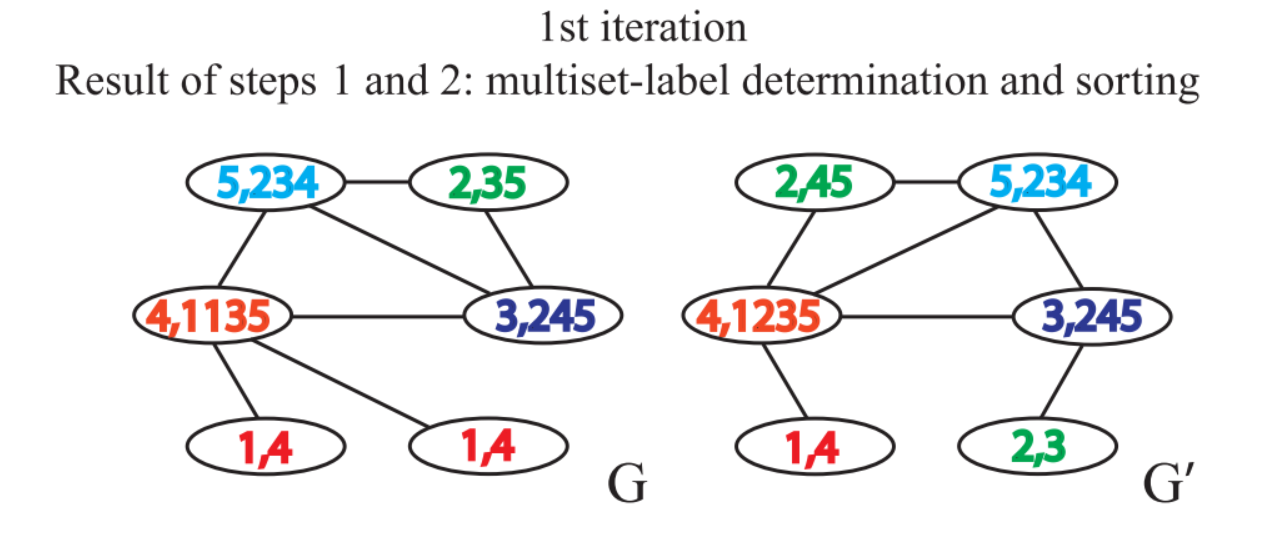
   
2. 标签散列，即标签压缩，将较长的字符串映射到一个简短的标签。
   
3. 给节点重新打上标签
   

每重复一次以上的过程，就完成一次节点自身标签与邻接节点标签的聚合。

当出现两个图相同节点标签的出现次数不一致时，即可判断两个图不相似。如果上述的步骤重复一定的次数后，没有发现有相同节点标签的出现次数不一致的情况，那么我们无法判断两个图是否同构。（所以这个算法只能准确的找到不同构的图）

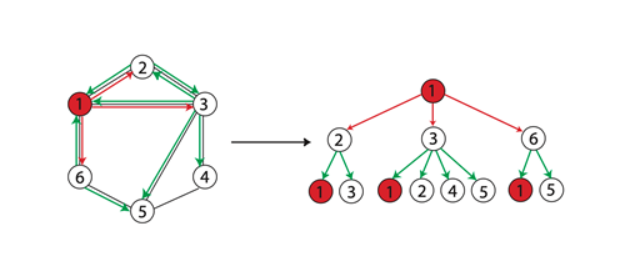
当两个节点的层的标签一样时，表示分别以这两个节点为根节点的WL子树是一致的。WL子树与普通子树不同，WL子树包含重复的节点。下图展示了一棵以1节点为根节点高为2的WL子树。

1.3.4.2 图相似性评估

（此方法来自于论文《Weisfeiler-Lehman Graph Kernels》）

WL Test 算法的一点局限性是，它只能判断两个图的相似性，无法衡量图之间的相似性。要衡量两个图的相似性，我们用WL Subtree Kernel方法。该方法的思想是用WL Test算法得到节点的多层的标签，然后我们可以分别统计图中各类标签出现的次数，存于一个向量，这个向量可以作为图的表征。两个图的表征向量的内积，即可作为这两个图的相似性估计，内积越大表示相似性越高。

1.3.5 为什么 WL Test 是GNNs性能的上限

• 假设两个图和是非同构的，如果存在一个图神经网络： 可以将图和映射到不同的表征向量，那么Weisfeiler-Lehman Test 同样也可以确定图和是非同构的。

这里略去证明。上面这个定义的意思就是如果GNNs能判断两个图是非同构的，那么WL Test也一定可以，这就说明了GNNs性能的上限是WL Test 。

1.3.6 什么样的GNNs可以达到该上限

• 对于一个图神经网络 和 两个通过Weisfeiler-Lehman Test 确定为不同构的两个图和，在GNN层足够多的情况下，如果该图神经网络可以确定图和是非同构的，则说明该图神经网络达到了其性能上限。

那么，满足什么条件的GNNs才可以说是达到了该上限呢？结合之前可重复集合和单射函数的定义以及图神经网络三个核心模块的回顾，可以发现，当GNNs的聚合和更新函数满足如下条件时，该GNNs性能达到了上限

%7D%20%3D%20%5Cphi(h_v%5E%7B(k-1)%7D%2C%20f(%5C%7Bh_u%5E%7B(k-1)%7D%2C%20u%20%5Cin%20%5Cmathcal%7BN%7D(v)%20%5C%7D))%0A#card=math&code=h_v%5E%7B%28k%29%7D%20%3D%20%5Cphi%28h_v%5E%7B%28k-1%29%7D%2C%20f%28%5C%7Bh_u%5E%7B%28k-1%29%7D%2C%20u%20%5Cin%20%5Cmathcal%7BN%7D%28v%29%20%5C%7D%29%29%0A&id=b6lDd)

其中，

• 函数作用在可重复集合上
• 函数是单射的

这部分的证明也省略。总的来说，如果一个GNNs可以识别不同的邻域结构，那它的性能就达到了上限。

2. 图同构神经网络（Graph Isomorphism Network，GIN）

为了研究GNNs的表征能力，可以分析GNNs将两个节点映射到表示空间的同一位置时的表征能力，所以可以将分析简化为这样一个问题：

• GNNs是否可以将不同的图结构（即两个多集合）映射为相同的表示向量

这种将任意两个不同的图映射为不同的表征向量的能力意味着要解决具有挑战性的图同构问题。也就是说，希望同构图的表征向量相同，非同构图的表征向量不同。一个强大的GNN不会将两个不同的邻域映射到相同的表征向量，这就意味着它的聚合模式必须是单射的。因此，文中将一个GNNs的聚合方案抽象为一类神经网络可以表征的作用于可重复集合上的函数。

除了区分不同的图之外，GNNs还有一个值得讨论的重要优点，即捕获图结构的相似性。WL测试中的节点特征向量本质上是one-hot编码，因此不能捕获子树之间的相似性。相反，性能达到上限的GNN通过学习将子树嵌入到低维空间来推广WL测试。这使得GNN不仅能够区分不同的结构，而且还能够学习将类似的图结构映射到类似的 embeddings，并捕获图结构之间的依赖关系。因此，文中提出了一个网络架构，称为 Graph Isomorphism Network (GIN) 图同构网络，这个网络性能达到了上限，并且对 WL Test 进行了推广，从而在GNNs中的表征能力最强。

2.1 构建图同构神经网络（GIN）

先来介绍一个定理，

• 当可数时，将聚合方式设置为sum，更新函数设置为时，会存在函数#card=math&code=f%28x%29&id=qxeir)，使#card=math&code=h%28c%2CX%29&id=tuGQ8)为单射函数： %20%3D%20(1%20%2B%20%CF%B5)%C2%B7f(c)%20%2B%20%5Csum%7Bx%20%5Cin%20X%7Df(x)%0A#card=math&code=h%28c%2CX%29%20%3D%20%281%20%2B%20%CF%B5%29%C2%B7f%28c%29%20%2B%20%5Csum%7Bx%20%5Cin%20X%7Df%28x%29%0A&id=VZcTo)
  其中，

  • c为节点自身特征
  • X为邻域特征集

  
  由这个定理可以进一步推出，对于任意#card=math&code=g%28c%2C%20X%29&id=lsKW2)，都可以分解成以下的形式，满足单射性：

%20%3D%20%CF%86((1%20%2B%20%CF%B5)%C2%B7f(c)%20%2B%20%5Csum%7Bx%20%5Cin%20X%7Df(x))%0A#card=math&code=g%28c%2C%20X%29%20%3D%20%CF%86%28%281%20%2B%20%CF%B5%29%C2%B7f%28c%29%20%2B%20%5Csum%7Bx%20%5Cin%20X%7Df%28x%29%29%0A&id=X1dSi)

通过引入多层感知机去学习和来保证单射性，最终得到基于MLP+sum的GIN框架：

%7D%20%3D%20MLP%5E%7B(k)%7D((1%20%2B%20%CF%B5%5E%7B(k)%7D)%C2%B7hv%5E%7B(k-1)%7D%20%2B%20%5Csum%7Bu%20%5Cin%20%5Cmathcal%7BN%7D(v)%7Dhu%5E%7B(k-1)%7D)%0A#card=math&code=h_v%5E%7B%28k%29%7D%20%3D%20MLP%5E%7B%28k%29%7D%28%281%20%2B%20%CF%B5%5E%7B%28k%29%7D%29%C2%B7h_v%5E%7B%28k-1%29%7D%20%2B%20%5Csum%7Bu%20%5Cin%20%5Cmathcal%7BN%7D%28v%29%7Dh_u%5E%7B%28k-1%29%7D%29%0A&id=id7Zt)

• MLP可以近似拟合任意函数，故可以学习到单射函数，而GraphSAGE和GCN中使用的单层感知机不能满足。
• 约束输入特征是one-hot，故第一次迭代sum后还是满足单射性，不需先做MLP的预处理。
• 由于%7D#card=math&code=h_v%5E%7B%280%29%7D&id=Rm73t)是可数的，根据论文中定理，迭代k轮得到新特征%7D#card=math&code=h_v%5E%7B%28k%29%7D&id=Bfp2e)是可数的，经过了转换#card=math&code=f%28x%29&id=SshEE)，下一轮迭代还是满足单射性条件。

2.2 图级别任务中的GIN

通过GIN学习的节点表征向量可以用于类似于节点分类、边预测这样的任务。而对于图分类任务，文中提出了一个READOUT函数：给定独立的节点的表征向量集，生成整个图的表征向量。

GIN的READOUT模块使用concat+sum，对每次迭代得到的所有节点特征求和得到图的特征，然后拼接起来，公式如下：

%7D%7Cv%20%5Cin%20G%5C%7D)%2C%20k%20%3D%200%2C1%2C%20…%2C%20K)%0A#card=math&code=h_G%20%3D%20CONCAT%28READOUT%28%5C%7Bh_v%5E%7B%28k%29%7D%7Cv%20%5Cin%20G%5C%7D%29%2C%20k%20%3D%200%2C1%2C%20…%2C%20K%29%0A&id=ZyrBv)

%7D%7Cv%20%5Cin%20G%5C%7D)%2C%20k%20%3D%200%2C1%2C%20…%2C%20K)%0A#card=math&code=h_G%20%3D%20CONCAT%28sum%28%5C%7Bh_v%5E%7B%28k%29%7D%7Cv%20%5Cin%20G%5C%7D%29%2C%20k%20%3D%200%2C1%2C%20…%2C%20K%29%0A&id=uEWGk)

3. 基于GIN的图表征学习

基于图同构网络的图表征学习主要包含以下两个过程：

1. 首先计算得到节点表征；
2. 其次对图上各个节点的表征做图池化（Graph Pooling），或称为图读出（Graph Readout），得到图的表征（Graph Representation）。

在本节中，我们将采用自顶向下的方式，来学习基于图同构模型（GIN）的图表征学习方法。首先关注如何基于节点表征计算得到图的表征，而忽略计算结点表征的方法。

3.1 基于图同构网络的图表征模块

• 此模块首先采用**GINNodeEmbedding**对图上每一个节点做节点嵌入（Node Embedding），得到节点表征；
  GINNodeEmbedding的源码如下：
  【注意】：使用GINNodeEmbedding模块要导入资料中的gin_regression，并添加为source。 ```python import torch from mol_encoder import AtomEncoder from gin_conv import GINConv import torch.nn.functional as F

GNN to generate node embedding

class GINNodeEmbedding(torch.nn.Module): “”” Output: node representations “””

def __init__(self, num_layers, emb_dim, drop_ratio=0.5, JK="last", residual=False):
    """
    GIN Node Embedding Module
    采用多层GINConv实现图上结点的嵌入。
    """
    super(GINNodeEmbedding, self).__init__()
    self.num_layers = num_layers
    self.drop_ratio = drop_ratio
    # 选择图表征向量的连接方式
    self.JK = JK
    # 是否增加残差链接
    self.residual = residual
    if self.num_layers < 2:
        raise ValueError("Number of GNN layers must be greater than 1.")
    self.atom_encoder = AtomEncoder(emb_dim)
    # List of GNNs
    self.convs = torch.nn.ModuleList()
    self.batch_norms = torch.nn.ModuleList()
    for layer in range(num_layers):
        self.convs.append(GINConv(emb_dim))
        self.batch_norms.append(torch.nn.BatchNorm1d(emb_dim))
def forward(self, batched_data):
    x, edge_index, edge_attr = batched_data.x, batched_data.edge_index, batched_data.edge_attr
    # computing input node embedding
    h_list = [self.atom_encoder(x)]  # 先将类别型原子属性转化为原子嵌入
    for layer in range(self.num_layers):
        h = self.convs[layer](h_list[layer], edge_index, edge_attr)
        h = self.batch_norms[layer](h)
        if layer == self.num_layers - 1:
            # remove relu for the last layer
            h = F.dropout(h, self.drop_ratio, training=self.training)
        else:
            h = F.dropout(F.relu(h), self.drop_ratio, training=self.training)
        if self.residual:
            h += h_list[layer]
        h_list.append(h)
    # Different implementations of Jk-concat
    if self.JK == "last":
        node_representation = h_list[-1]
    elif self.JK == "sum":
        node_representation = 0
        for layer in range(self.num_layers + 1):
            node_representation += h_list[layer]
    return node_representation

-  然后**对节点表征做图池化得到图的表征**； 
-  **最后用一层线性变换对图表征转换为对图的预测**。 
代码实现如下：
```python
import torch
from torch import nn
from torch_geometric.nn import global_add_pool, global_mean_pool, global_max_pool, GlobalAttention, Set2Set
from gin_node import GINNodeEmbedding
class GINGraphRepr(nn.Module):
    def __init__(self, num_tasks=1, num_layers=5, emb_dim=300, residual=False, drop_ratio=0, JK='last', graph_pooling='sum'):
        """GIN Graph Pooling Module
        Args:
            num_tasks (int, optional): number of labels to be predicted. Defaults to 1 (控制了图表征的维度，dimension of graph representation).
            num_layers (int, optional): number of GINConv layers. Defaults to 5.
            emb_dim (int, optional): dimension of node embedding. Defaults to 300.
            residual (bool, optional): adding residual connection or not. Defaults to False.
            drop_ratio (float, optional): dropout rate. Defaults to 0.
            JK (str, optional): 可选的值为"last"和"sum"。选"last"，只取最后一层的结点的嵌入，选"sum"对各层的结点的嵌入求和。Defaults to "last".
            graph_pooling (str, optional): pooling method of node embedding. 可选的值为"sum"，"mean"，"max"，"attention"和"set2set"。 Defaults to "sum".
        Out:
            graph representation
        """
        super(GINGraphRepr, self).__init__()
        self.num_layers = num_layers
        self.drop_ratio = drop_ratio
        self.JK = JK
        self.emb_dim = emb_dim
        self.num_tasks = num_tasks
        if self.num_layers < 2:
            raise ValueError("Number of GNN layers must be greater than 1.")
        self.gnn_node = GINNodeEmbedding(num_layers, emb_dim, JK=JK, drop_ratio=drop_ratio, residual=residual)
        # 选择产生整个图的表征向量的池化方式
        if graph_pooling == "sum":
            self.pool = global_add_pool
        elif graph_pooling == "mean":
            self.pool = global_mean_pool
        elif graph_pooling == "max":
            self.pool = global_max_pool
        elif graph_pooling == "attention":
            self.pool = GlobalAttention(gate_nn=nn.Sequential(
                nn.Linear(emb_dim, emb_dim),
                nn.BatchNorm1d(emb_dim),
                nn.ReLU(),
                nn.Linear(emb_dim, 1)
            ))
        elif graph_pooling == "set2set":
            self.pool = Set2Set(emb_dim, processing_steps=2)
        else:
            raise ValueError("Invalid graph pooling type.")
        if graph_pooling == "set2set":
            self.graph_pred_linear = nn.Linear(2*self.emb_dim, self.num_tasks)
        else:
            self.graph_pred_linear = nn.Linear(self.emb_dim, self.num_tasks)
    def forward(self, batched_data):
        h_node = self.gnn_node(batched_data)
        h_graph = self.pool(h_node, batched_data.batch)
        output = self.graph_pred_linear(h_graph)
        if self.training:
            return output
        else:
            # At inference time, relu is applied to output to ensure positivity
            # 因为预测目标的取值范围就在 (0, 50] 内
            return torch.clamp(output, min=0, max=50)

从代码中可以看到可选的基于结点表征计算得到图表征的方法有：

1. “sum”：
   • 原理：对节点表征求和；
   • 使用模块[torch_geometric.nn.glob.global_add_pool](https://pytorch-geometric.readthedocs.io/en/latest/modules/nn.html#torch_geometric.nn.glob.global_add_pool)。

1. “mean”：
   • 原理：对节点表征求平均；
   • 使用模块[torch_geometric.nn.glob.global_mean_pool](https://pytorch-geometric.readthedocs.io/en/latest/modules/nn.html#torch_geometric.nn.glob.global_mean_pool)。

1. “max”：
   • 原理：对一个batch中所有节点计算节点表征各个维度的最大值；
   • 使用模块[torch_geometric.nn.glob.global_max_pool](https://pytorch-geometric.readthedocs.io/en/latest/modules/nn.html#torch_geometric.nn.glob.global_max_pool)。

1. “attention”：
   （来自论文 “Gated Graph Sequence Neural Networks” 。）
   • 原理： %20%5Cright)%20%5Codot%0Ah%7B%5Cmathbf%7B%5CTheta%7D%7D%20(%20%5Cmathbf%7Bx%7D_n%20)%2C%0A#card=math&code=%5Cmathbf%7Br%7D_i%20%3D%20%5Csum%7Bn%3D1%7D%5E%7BNi%7D%20%5Cmathrm%7Bsoftmax%7D%20%5Cleft%28%0Ah%7B%5Cmathrm%7Bgate%7D%7D%20%28%20%5Cmathbf%7Bx%7Dn%20%29%20%5Cright%29%20%5Codot%0Ah%7B%5Cmathbf%7B%5CTheta%7D%7D%20%28%20%5Cmathbf%7Bx%7Dn%20%29%2C%0A&id=JnMqR)
     这里和表示多层感知机。
   • 参数：
     • gatenn ( torch.nn.Module ) ：神经网络通过将节点的特征x从[-1, in_channels]映射为[-1, 1]来计算注意力系数，这个网络可以由torch.nn.Sequential定义。
     • nn (torch.nn.Module , 可选) ：在与注意力系数相乘之前，神经网络将节点特征从[-1, in_channels]映射为[-1, out_channels]。这个网络同样可以由torch.nn.Sequential定义。（默认值：None`）

• 使用模块 torch_geometric.nn.glob.GlobalAttention。

1. “set2set”:
   （来自论文“Order Matters: Sequence to sequence for sets”。）
   • 原理：
     采用LSTM计算注意力系数，通过拼接的方式更新节点表征 %5C%5C%5Calpha%7Bi%2Ct%7D%20%26%3D%20%5Cmathrm%7Bsoftmax%7D(%5Cmathbf%7Bx%7D_i%20%5Ccdot%20%5Cmathbf%7Bq%7D_t)%5C%5C%5Cmathbf%7Br%7D_t%20%26%3D%20%5Csum%7Bi%3D1%7D%5EN%20%5Calpha%7Bi%2Ct%7D%20%5Cmathbf%7Bx%7D_i%5C%5C%5Cmathbf%7Bq%7D%5E%7B*%7D_t%20%26%3D%20%5Cmathbf%7Bq%7D_t%20%5C%2C%20%5CVert%20%5C%2C%20%5Cmathbf%7Br%7D_t%2C%5Cend%7Baligned%7D%5Cend%7Balign%7D%0A#card=math&code=%5Cbegin%7Balign%7D%5Cbegin%7Baligned%7D%5Cmathbf%7Bq%7D_t%20%26%3D%20%5Cmathrm%7BLSTM%7D%28%5Cmathbf%7Bq%7D%5E%7B%2A%7D%7Bt-1%7D%29%5C%5C%5Calpha%7Bi%2Ct%7D%20%26%3D%20%5Cmathrm%7Bsoftmax%7D%28%5Cmathbf%7Bx%7D_i%20%5Ccdot%20%5Cmathbf%7Bq%7D_t%29%5C%5C%5Cmathbf%7Br%7D_t%20%26%3D%20%5Csum%7Bi%3D1%7D%5EN%20%5Calpha_%7Bi%2Ct%7D%20%5Cmathbf%7Bx%7D_i%5C%5C%5Cmathbf%7Bq%7D%5E%7B%2A%7D_t%20%26%3D%20%5Cmathbf%7Bq%7D_t%20%5C%2C%20%5CVert%20%5C%2C%20%5Cmathbf%7Br%7D_t%2C%5Cend%7Baligned%7D%5Cend%7Balign%7D%0A&id=mKZ4m)
     由于最后是拼接操作，的维度是的两倍。
   • 参数：
     • in_channels (int) : 每个输入样本的特征维度
     • processing_steps (int) : 迭代次数
     • num_layers (int, 可选) ：递归层的数量，比如，设置 num_layers=2将意味着堆叠两层LSTM在一起以形成堆叠的LSTM层，第二层LSTM读入第一层LSTM的输出然后计算最终结果。（默认值：1）

• 使用模块 torch_geometric.nn.glob.Set2Set；

  
  PyG中集成的所有的图池化的方法可见于Global Pooling Layers。

【补充】：

• torch.clamp(input, min, max, out=None) → Tensor

  • 作用：将 input Tensor 中的每个元素夹紧到区间 [min, max] 内，并返回结果到一个新的 Tensor 。

  • 操作方式：

    | min, if x_i < min
    y_i = | x_i, if min <= x_i <= max
    | max, if x_i > max
    

  • 参数说明：

    • input (Tensor) ：输入张量
    • min (Number) ：限制范围下限
    • max (Number) ：限制范围上限
    • out (Tensor, optional) ：输出张量

3.2 基于图同构网络的节点嵌入模块

本节介绍的节点嵌入模块基于多层GINConv实现结点嵌入的计算。此处我们先忽略GINConv的实现。输入到此节点嵌入模块的节点属性为类别型向量，我们首先用**AtomEncoder**对其做嵌入得到第**0**层节点表征（稍后我们再对AtomEncoder做分析）。然后我们逐层计算节点表征，从第1层开始到第num_layers层，每一层节点表征的计算都以上一层的节点表征**h_list[layer]**、边**edge_index**和边的属性**edge_attr**为输入。需要注意的是，GINConv的层数越多，此节点嵌入模块的感受野（receptive field）越大，结点**i**的表征最远能捕获到结点**i**的距离为**num_layers**的邻接节点的信息（即捕捉 num_layers-hop邻居的信息）。

import torch
from mol_encoder import AtomEncoder
from gin_conv import GINConv
import torch.nn.functional as F

# 通过GNN产生节点表征
class GINNodeEmbedding(torch.nn.Module):
    """
    Output:
        node representations
    """

    def __init__(self, num_layers, emb_dim, drop_ratio=0.5, JK="last", residual=False):
        """GIN Node Embedding Module"""

        super(GINNodeEmbedding, self).__init__()
        self.num_layers = num_layers
        self.drop_ratio = drop_ratio
        self.JK = JK
        # 是否增加残差连接
        self.residual = residual

        if self.num_layers < 2:
            raise ValueError("Number of GNN layers must be greater than 1.")

        self.atom_encoder = AtomEncoder(emb_dim)

        # 定义网络
        self.convs = torch.nn.ModuleList()
        self.batch_norms = torch.nn.ModuleList()

        for layer in range(num_layers):
            self.convs.append(GINConv(emb_dim))
            self.batch_norms.append(torch.nn.BatchNorm1d(emb_dim))

    def forward(self, batched_data):
        x, edge_index, edge_attr = batched_data.x, batched_data.edge_index, batched_data.edge_attr

        # 计算输入节点的表征向量
        h_list = [self.atom_encoder(x)]  # 先将类别型原子属性转化为原子表征
        for layer in range(self.num_layers):
            h = self.convs[layer](h_list[layer], edge_index, edge_attr)
            h = self.batch_norms[layer](h)
            if layer == self.num_layers - 1:
                # 最后一层不使用relu激活
                h = F.dropout(h, self.drop_ratio, training=self.training)
            else:
                h = F.dropout(F.relu(h), self.drop_ratio, training=self.training)

            if self.residual:
                h += h_list[layer]

            h_list.append(h)

        # 选择不同的策略形成节点表征向量
        if self.JK == "last":
            node_representation = h_list[-1]
        elif self.JK == "sum":
            node_representation = 0
            for layer in range(self.num_layers + 1):
                node_representation += h_list[layer]

        return node_representation

3.3 图同构卷积层GINConv

图同构卷积层的数学定义如下：

%20%5Ccdot%0A%5Cmathbf%7Bx%7Di%20%2B%20%5Csum%7Bj%20%5Cin%20%5Cmathcal%7BN%7D(i)%7D%20%5Cmathbf%7Bx%7Dj%20%5Cright)%0A#card=math&code=%5Cmathbf%7Bx%7D%5E%7B%5Cprime%7D_i%20%3D%20h%7B%5Cmathbf%7B%5CTheta%7D%7D%20%5Cleft%28%20%281%20%2B%20%5Cepsilon%29%20%5Ccdot%0A%5Cmathbf%7Bx%7Di%20%2B%20%5Csum%7Bj%20%5Cin%20%5Cmathcal%7BN%7D%28i%29%7D%20%5Cmathbf%7Bx%7D_j%20%5Cright%29%0A&id=a62Mo)

PyG中已经实现了此模块，我们可以通过[torch_geometric.nn.GINConv](https://pytorch-geometric.readthedocs.io/en/latest/modules/nn.html#torch_geometric.nn.conv.GINConv)来使用PyG定义好的图同构卷积层，然而该实现不支持存在边属性的图。在这里我们自己自定义一个支持边属性的**GINConv**模块。

由于输入的边属性为类别型，因此我们需要先将类别型边属性转换为边表征。我们定义的GINConv模块遵循“消息传递、消息聚合、消息更新”这一过程。

• 这一过程随着self.propagate()方法的调用开始执行，该函数接收edge_index, x, edge_attr此三个参数。edge_index是形状为[2,num_edges]的张量（Tensor）。
• 在消息传递过程中，此张量首先被按行拆分为**x_i**和**x_j**张量，**x_j**表示了消息传递的源节点，**x_i**表示了消息传递的目标节点。
• 接着message()方法被调用，此函数定义了从源节点传入到目标节点的消息，在这里要传递的消息是源节点表征与边表征之和的relu()的输出。我们在super(GINConv, self).__init__(aggr = "add")中定义了消息聚合方式为add，那么传入给任一个目标节点的所有消息被求和得到aggr_out，它还是目标节点的中间过程的信息。
• 接着执行消息更新过程，我们的类GINConv继承了MessagePassing类，因此update()函数被调用。然而我们希望对节点做消息更新中加入目标节点自身的消息，因此在update函数中我们只简单返回输入的aggr_out。
• 然后在forward函数中我们执行out = self.mlp((1 + self.eps) *x + self.propagate(edge_index, x=x, edge_attr=edge_embedding))实现消息的更新（这里就是上面介绍的公式的代码形式）。

import torch
from torch import nn
from torch_geometric.nn import MessagePassing
import torch.nn.functional as F
from ogb.graphproppred.mol_encoder import BondEncoder

class GINConv(MessagePassing):

    def __init__(self, emb_dim):
        '''
            emb_dim(int): 节点表征维度
        '''
        super(GINConv, self).__init__(aggr="add")

        self.mlp = nn.Sequential(
            nn.Linear(emb_dim, emb_dim),
            nn.BatchNorm1d(emb_dim),
            nn.ReLU(),
            nn.Linear(emb_dim, emb_dim)
        )

        self.eps = nn.Parameter(torch.Tensor([0]))
        self.bond_encoder = BondEncoder(emb_dim=emb_dim)

    def forward(self, x, edge_index, edge_attr):
        # 先将类别型边属性转换为边表征
        edge_embedding = self.bond_encoder(edge_attr)

        out = self.mlp((1 + self.eps) * x + self.propagate(edge_index, x=x, edge_attr=edge_embedding))
        return out

    def message(selfself, x_j, edge_attr):
        return F.relu(x_j + edge_attr)

    def update(self, aggr_out):
        return aggr_out

3.4 AtomEncoder 与 BondEncoder

由于在当前的例子中，节点（原子）和边（化学键）的属性都为离散值，它们属于不同的空间，无法直接将它们融合在一起。通过嵌入（Embedding），我们可以将节点属性和边属性分别映射到一个新的空间，在这个新的空间中，我们就可以对节点和边进行信息融合。在GINConv中，**message()**函数中的**x_j + edge_attr** 操作执行了节点信息和边信息的融合。

接下来，我们通过下方的代码中的AtomEncoder类，来分析将节点属性映射到一个新的空间是如何实现的：

import torch
from ogb.utils.features import get_atom_feature_dims, get_bond_feature_dims 

full_atom_feature_dims = get_atom_feature_dims()
full_bond_feature_dims = get_bond_feature_dims()

class AtomEncoder(torch.nn.Module):

    def __init__(self, emb_dim):
        super(AtomEncoder, self).__init__()

        self.atom_embedding_list = torch.nn.ModuleList()

        for i, dim in enumerate(full_atom_feature_dims):
            emb = torch.nn.Embedding(dim, emb_dim)
            torch.nn.init.xavier_uniform_(emb.weight.data)
            self.atom_embedding_list.append(emb)

    def forward(self, x):
        x_embedding = 0
        for i in range(x.shape[1]):
            x_embedding += self.atom_embedding_list[i](x[:,i])

        return x_embedding


class BondEncoder(torch.nn.Module):

    def __init__(self, emb_dim):
        super(BondEncoder, self).__init__()

        self.bond_embedding_list = torch.nn.ModuleList()

        for i, dim in enumerate(full_bond_feature_dims):
            emb = torch.nn.Embedding(dim, emb_dim)
            torch.nn.init.xavier_uniform_(emb.weight.data)
            self.bond_embedding_list.append(emb)

    def forward(self, edge_attr):
        bond_embedding = 0
        for i in range(edge_attr.shape[1]):
            bond_embedding += self.bond_embedding_list[i](edge_attr[:,i])

        return bond_embedding   


if __name__ == '__main__':
    # 这里的loader需要自己定义
    from loader import GraphClassificationPygDataset
    dataset = GraphClassificationPygDataset(name = 'tox21')
    atom_enc = AtomEncoder(100)
    bond_enc = BondEncoder(100)

    print(atom_enc(dataset[0].x))
    print(bond_enc(dataset[0].edge_attr))

• full_atom_feature_dims 是一个list，存储了节点属性向量每一维可能取值的数量，即X[i]可能的取值一共有full_atom_feature_dims[i]种情况，X为节点属性；
• 节点属性有多少维，那么就需要有多少个嵌入函数，通过调用**torch.nn.Embedding(dim, emb_dim)**可以实例化一个嵌入函数；
• torch.nn.Embedding(dim, emb_dim)，第一个参数dim为被嵌入数据可能取值的数量，第一个参数emb_dim为要映射到的空间的维度。得到的嵌入函数接受一个大于0小于dim的数，输出一个维度为emb_dim的向量。嵌入函数也包含可训练参数，通过对神经网络的训练，嵌入函数的输出值能够表达不同输入值之间的相似性。
• 在forward()函数中，我们对不同属性值得到的不同嵌入向量进行了相加操作，实现了将节点的的不同属性融合在一起。

BondEncoder类与AtomEncoder类是类似的。

【补充】：

pytorch nn.init 中实现的初始化函数

1. 均匀分布：
   torch.nn.init.uniform_(tensor, a=0, b=1)
2. 标准正态分布：
   torch.nn.init.normal_(tensor, mean=0, std=1)
3. 初始化为常数：
   torch.nn.init.constant_(tensor, val)
   该函数会将整个矩阵初始化为常数val
4. Xavier初始化函数
   • 基本思想：在通过网络层时，输入和输出的方差相同，包括前向传播和后向传播。
   • 为什么需要Xavier初始化？
     • 如果初始化值很小，那么随着层数的传递，方差就会趋于0，此时输入值也变得越来越小，在sigmoid上就是在0附近，接近于线性，失去了非线性。
     • 如果初始值很大，那么随着层数的传递，方差会迅速增加，此时输入值变得很大，而sigmoid在大输入值写倒数趋近于0，反向传播时会遇到梯度消失的问题。

• 两种Xavier初始化方式：
  • torch.nn.init.xavier_uniform_(tensor, gain=1):
    • 服从均匀分布#card=math&code=U%28-a%2C%20a%29&id=rWDUk)
    • a的计算公式如下：
      

  -  `torch.nn.init.xavier_normal_(tensor, gain=1))`: 
     -  服从正态分布![](https://g.yuque.com/gr/latex?N(0%2C%20std)#card=math&code=N%280%2C%20std%29&id=YFg9S) 
     -  std的计算公式如下：<br />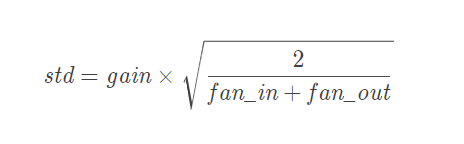![image-20210703194538936.png](https://cdn.nlark.com/yuque/0/2021/png/8424773/1625385291954-fd02e1aa-7bcf-4a5c-9e23-f0fb39832f04.png#clientId=ub51e23ec-730f-4&from=ui&id=udc255d39&margin=%5Bobject%20Object%5D&name=image-20210703194538936.png&originHeight=144&originWidth=464&originalType=binary&ratio=1&size=7687&status=done&style=none&taskId=u17f9fff4-441a-4537-abb6-fe4488498b5)

1. Kaiming 初始化
   • 作用：Xavier在tanh中表现的很好，但在Relu激活函数中表现的很差，所以何凯明提出了针对于Relu的初始化方法。
   • 原理：在ReLU网络中，假定每一层有一半的神经元被激活，另一半为0，所以，要保持方差不变，只需要在 Xavier 的基础上再除以2，也就是说在方差推导过程中，式子左侧除以2。
   • 两种Kaiming 初始化方式：
     • torch.nn.init.kaiming_uniform_(tensor, a=0, mode=‘fan_in’, nonlinearity=‘leaky_relu’)
       • 服从均匀分布#card=math&code=U%28-bound%2C%20bound%29&id=yH19R)
       • bound的计算公式如下：
         

  -  `torch.nn.init.kaiming_normal_(tensor, a=0, mode=‘fan_in’, nonlinearity=‘leaky_relu’)` 
     -  服从正态分布![](https://g.yuque.com/gr/latex?N(std%2C-std)#card=math&code=N%28std%2C-std%29&id=eynvt) 
     -  std的计算公式如下：<br />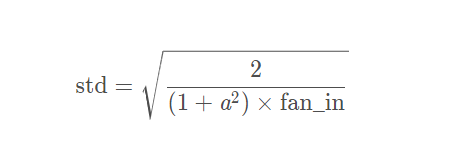![image-20210703195034648.png](https://cdn.nlark.com/yuque/0/2021/png/8424773/1625385308241-12295eb4-c699-4fc1-bddc-f77475c69e21.png#clientId=ub51e23ec-730f-4&from=ui&id=ucd0e070f&margin=%5Bobject%20Object%5D&name=image-20210703195034648.png&originHeight=162&originWidth=465&originalType=binary&ratio=1&size=5744&status=done&style=none&taskId=u418216e2-2f53-4e5b-9c31-e0019406b73)
  -  参数说明： 
     - `a`：**该层后面一层的激活函数中负的斜率**（默认为ReLU，此时a=0）
     - `mode`：‘fan_in’ (default) 或者 ‘fan_out’。使用fan_in保持weights的方差在前向传播中不变；使用fan_out保持weights的方差在反向传播中不变。

4. 实验部分

文中在9个数据集上进行了图分类任务，其中有四个生物信息学数据集（MUTAG，PTC，NCI1，PROTEINS），五个社交网络数据集（OLLAB，IMDB_BINARY，IMDB-MULTI，REDDIT-BINARY，REDDIT-MULTI5K）。

• 在训练集上的效果
  
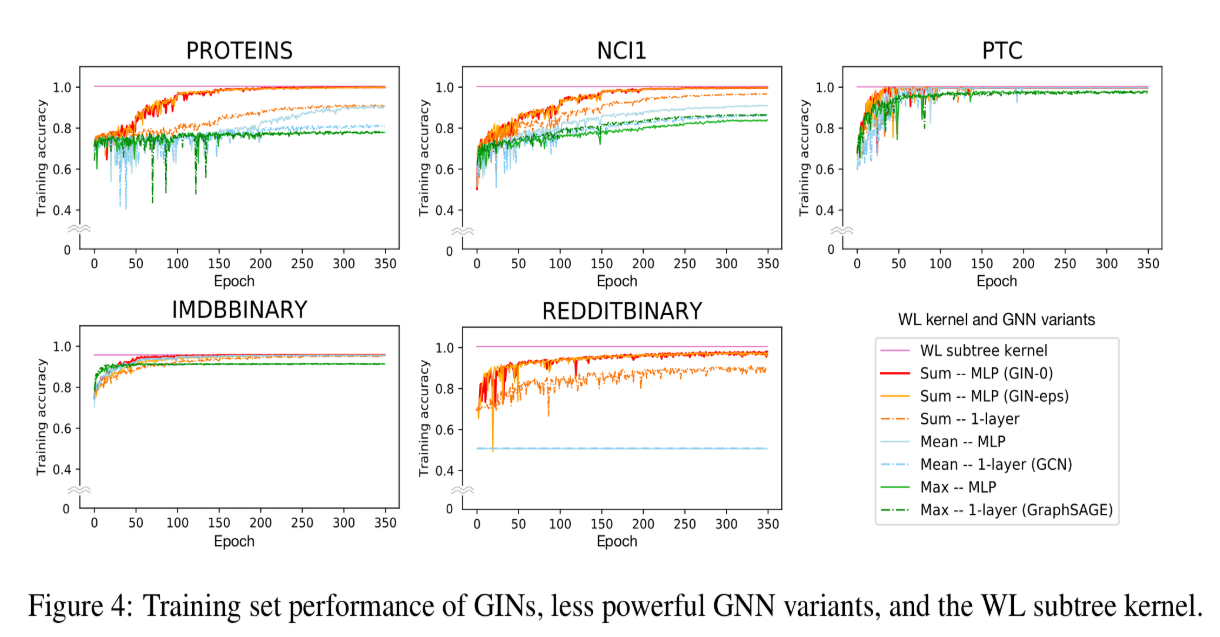
• 在测试集上的效果

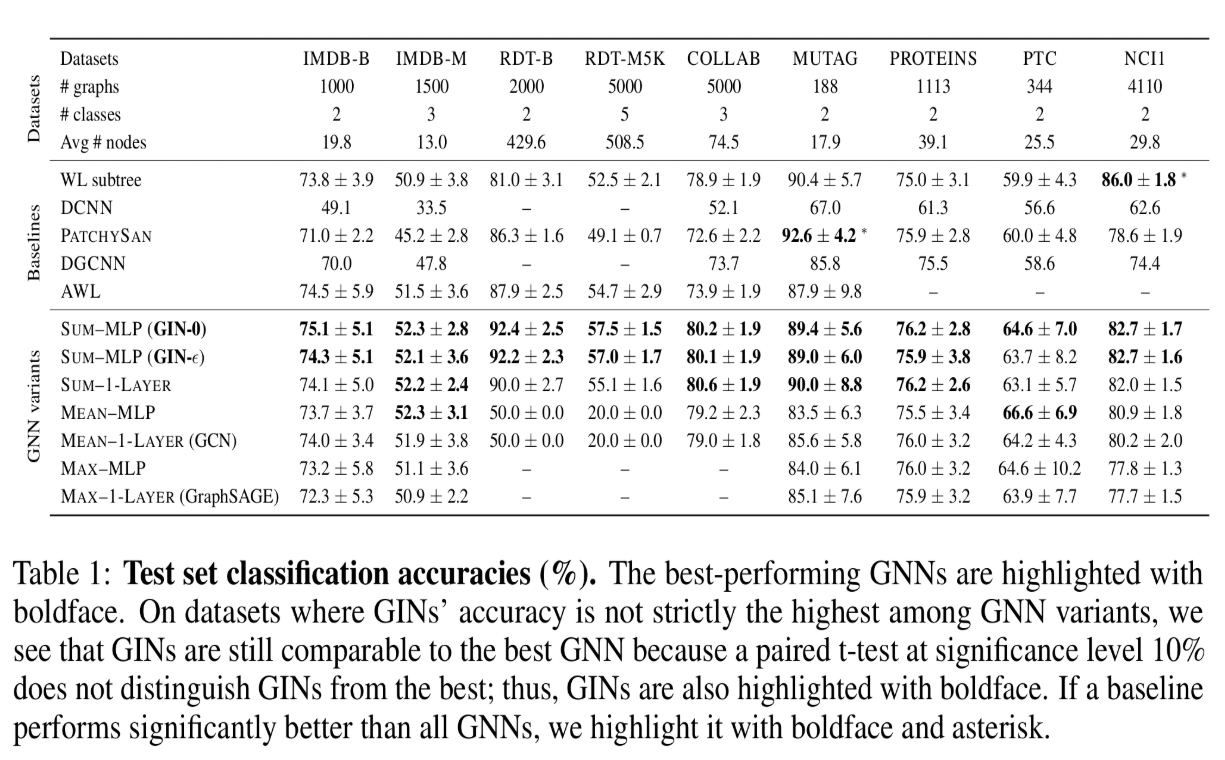
实验结论如下：

• GIN-0 比 GIN-ϵ 泛化能力强，可能是因为GIN-0更简单
• GIN 比 WL test 效果好，因为 GIN 进一步考虑了结构相似性，即 WL test 最终是 one-hot 输出，而GIN是将 WL test 映射到低维的表征向量
• max 在无节点特征的图（用度来表示特征）基本无效

5. 作业

请画出下方图片中的6号、3号和5号节点的从1层到3层的WL子树。

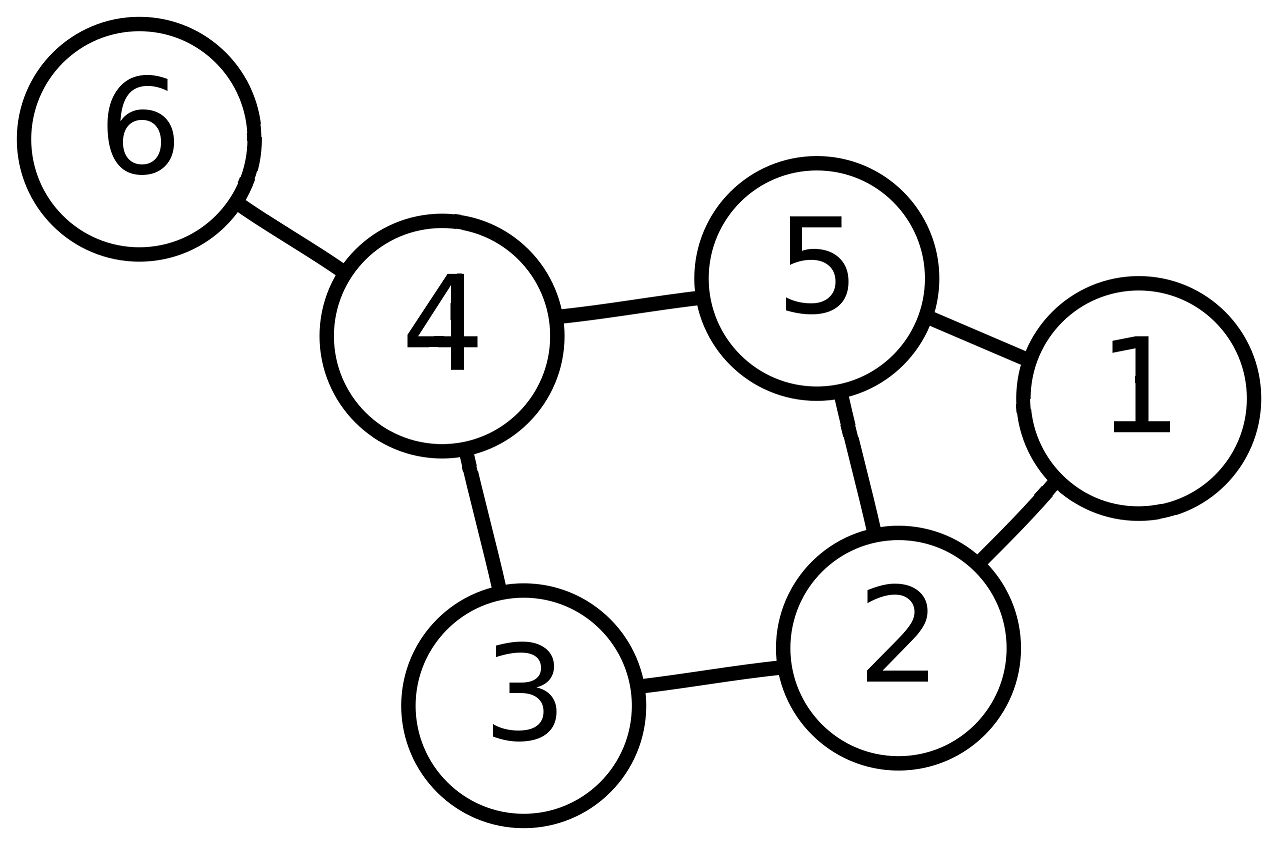
下面以6号节点为例画出3层WL子树，6号节点的消息传播流程如下图所示

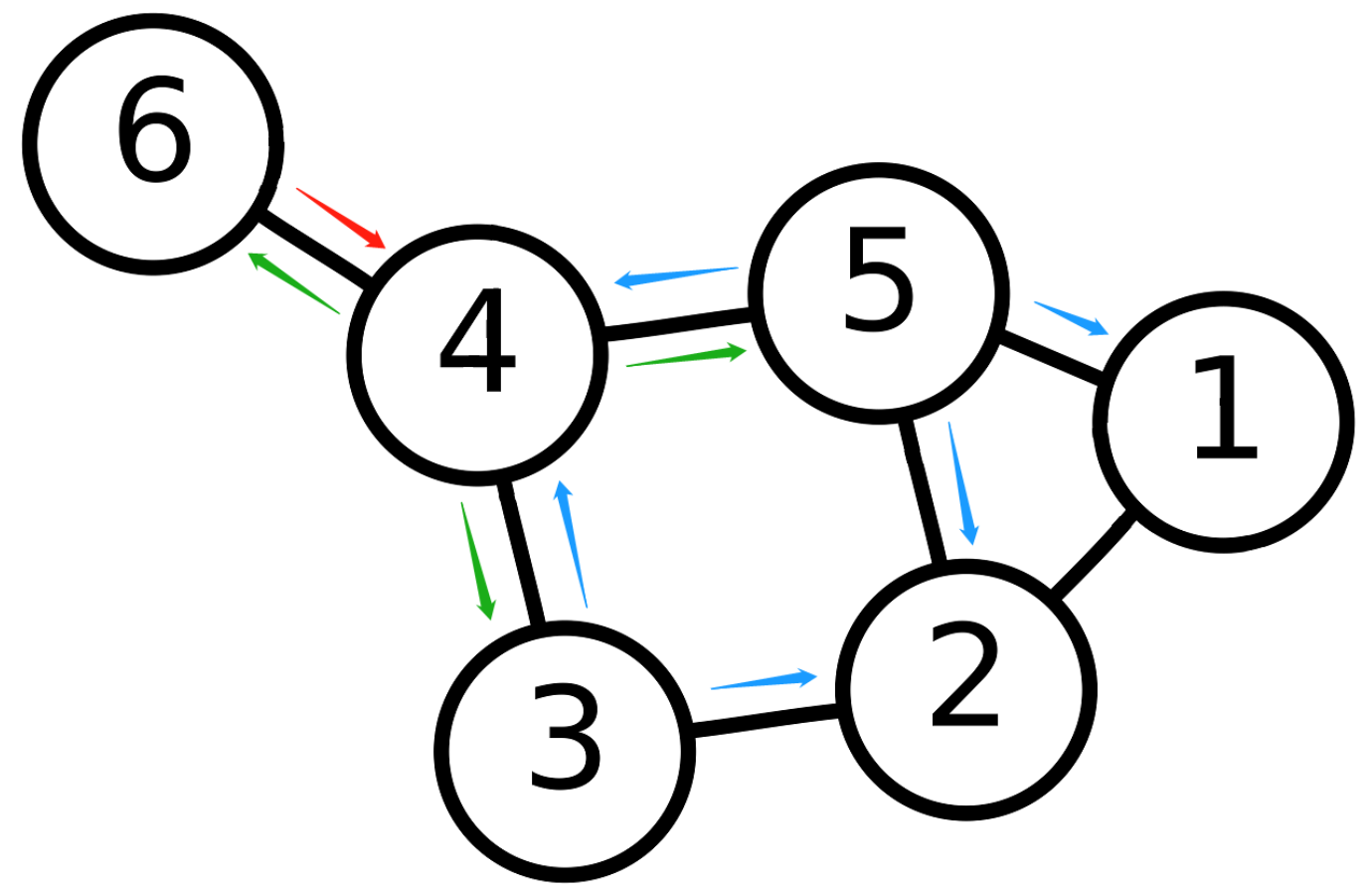
形成的3层WL子树如下：

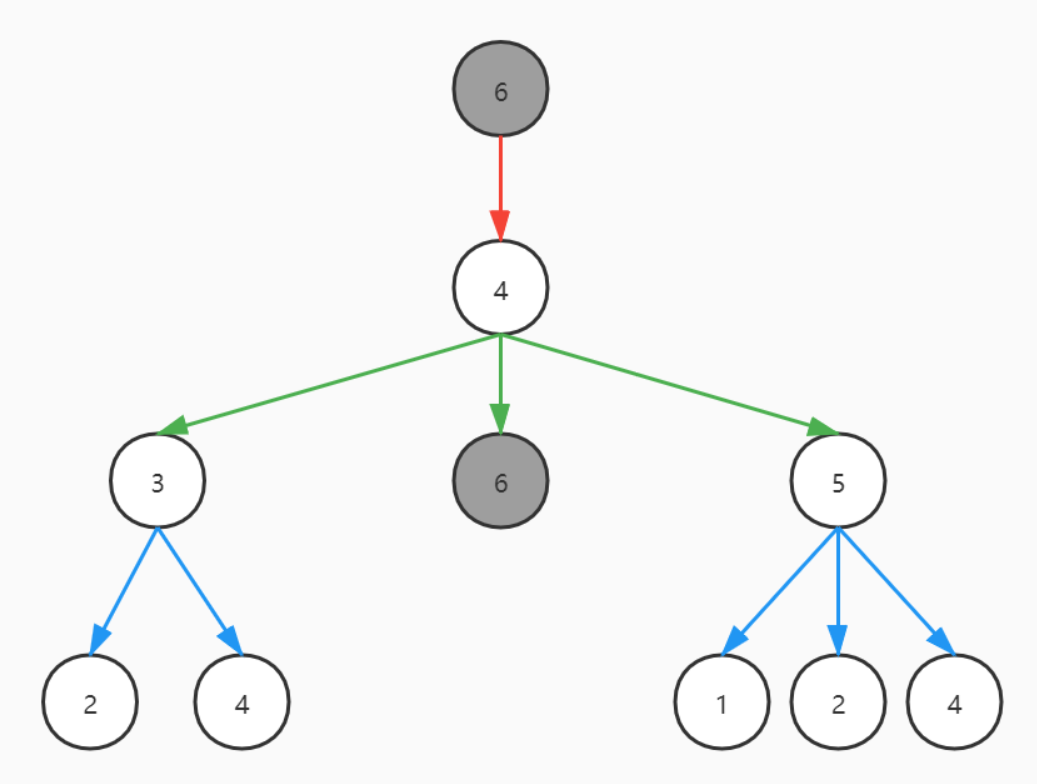
3号和5号节点同理。

6. 参考资料

• DataWhale开源学习资料：https://github.com/datawhalechina/team-learning-nlp/tree/master/GNN
• PyG官方文档：https://pytorch-geometric.readthedocs.io/en/latest/modules/nn.html#global-pooling-layers
• CSDN博客：https://blog.csdn.net/yyl424525/article/details/102841352
• tox21数据集：
• GIN论文：https://arxiv.org/abs/1810.00826
• cs224w：http://web.stanford.edu/class/cs224w/