Legendre functions

NIST_Handbook_Mathematical_Functions.pdf
这本书的第14章351页给出了Legendre函数的定义，以及实参数和复参数的Legendre函数的表达式。

E. T. Whittaker, G. N. Watson - A Course of Modern Analysis-Cambridge University Press (2021).pdf.pdf%22%2C%22size%22%3A10459778%2C%22type%22%3A%22application%2Fpdf%22%2C%22ext%22%3A%22pdf%22%2C%22source%22%3A%22%22%2C%22status%22%3A%22done%22%2C%22mode%22%3A%22title%22%2C%22download%22%3Atrue%2C%22taskId%22%3A%22uf1844589-359f-49f5-bc36-fcdb2802982%22%2C%22taskType%22%3A%22upload%22%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22u15ac6918%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22file%22%7D)
这本书的第15章 P 369 开始讲Legendre 多项式。 通过定义 Legendre 多项式 p369，找到它的积分形式(p370)，再将其代入到 Legendre 方程中 (p371) 中证明其满足方程。
15.2 (p373) 中， 对于非整数的参数，利用复积分来定义 Legendre 函数。
15.3 (p384) 中， 给出了第二类 Legendre 函数， 通过复积分定义。作为方程的另外一个线性无关的解。
Example 15.3.4 (p386) 给出了 Q_1 的计算， 通过利用迭代公式计算15.3的积分。

第一类 Legendre 函数 定义为如下的复积分

其中周线 满足函数 绕 一周后值不变。

参考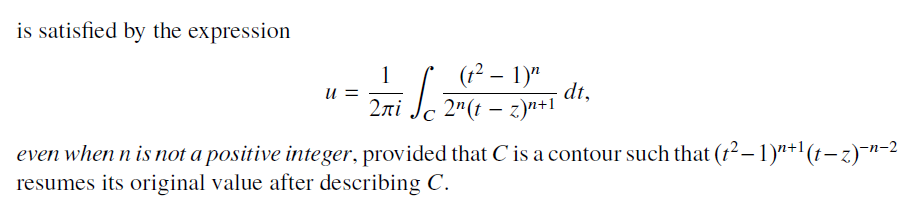

当 时, 第二类 Legendre 函数 定义为 如下的复积分

当 时，

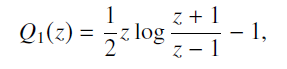
参考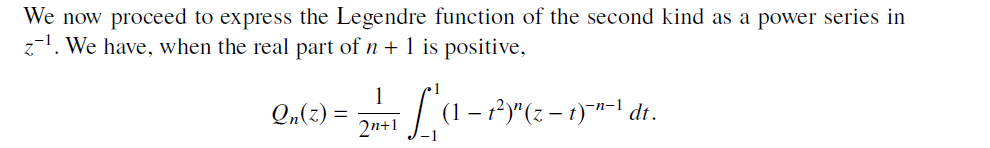

Lebedev N. N., Silverman R. A. - Special Functions and Their Applications (1972).pdf.pdf%22%2C%22size%22%3A9602959%2C%22type%22%3A%22application%2Fpdf%22%2C%22ext%22%3A%22pdf%22%2C%22source%22%3A%22%22%2C%22status%22%3A%22done%22%2C%22mode%22%3A%22title%22%2C%22download%22%3Atrue%2C%22taskId%22%3A%22u40f60c21-4a70-4873-8b72-3c94615b67c%22%2C%22taskType%22%3A%22upload%22%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22u2a2c4774%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22file%22%7D)
第7章中利用双曲几何级数定义 Legendre 函数以及相关的性质。

特殊函数概论中的定义

参数为整数的定义

勒让德函数定义为勒让德方程的解。

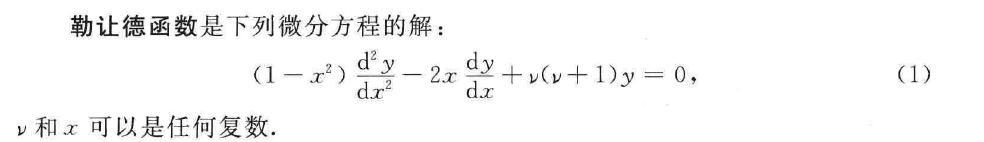
当 是整数时，第一类勒让德函数定义为

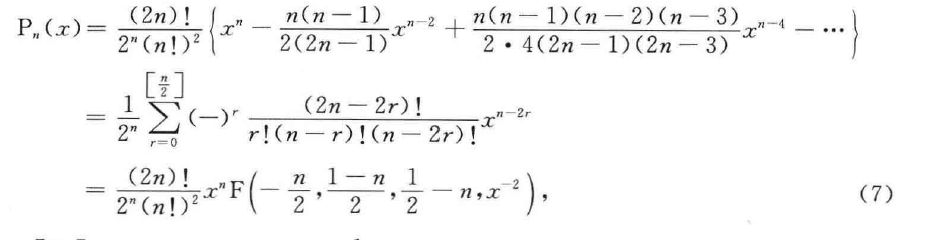
其中 为超几何函数表达式。

第二类勒让德函数定义为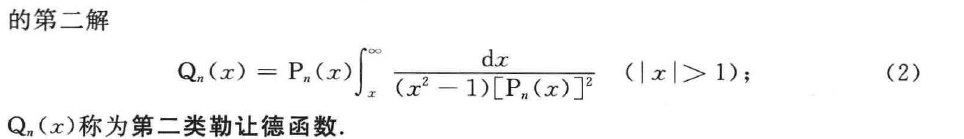

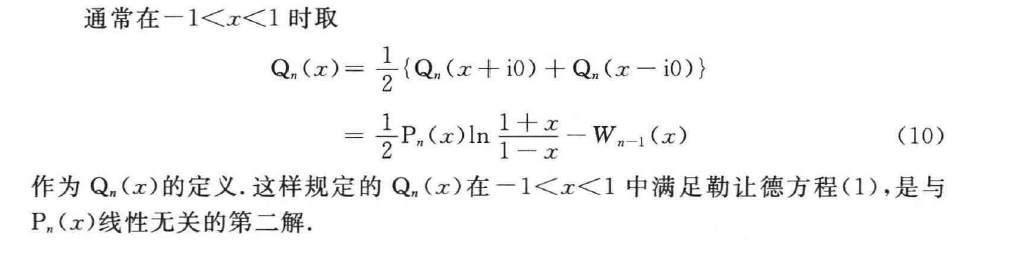
一般参数的定义

定义非常复杂，要用复积分来定义。

连带勒让德方程为

第一类勒让德函数的定义

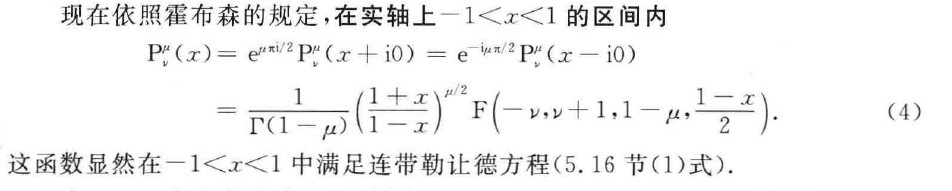
第二类勒让德函数的定义

在夹缝上定义为