加权 Soblev 空间

文献1

:::info 以下内容来自于 ArXiv：https://arxiv.org/pdf/math/0703725.pdf [1] :::

范数形如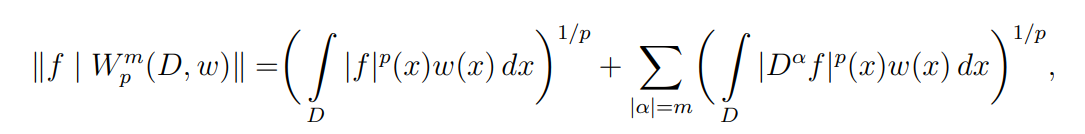

其中权为

权满足 条件时，Thm1说确实为Banach空间。 条件 如下

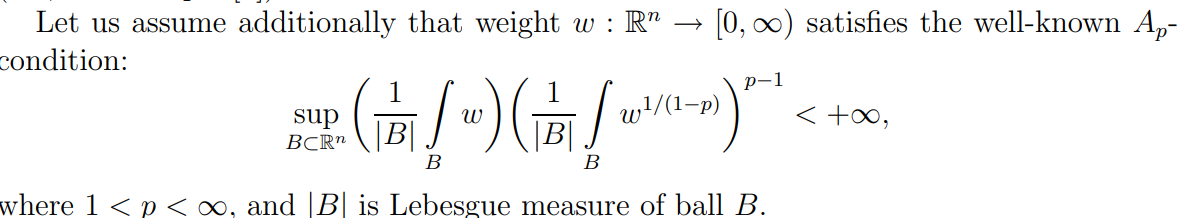
对于权 , , 可以验证上述条件是对所有 成立的.

文章给了满足特定条件区域上的紧嵌入定理

对权 , 选取适当的 可知 是成立的.

这篇文章后附上了很多参考文献。

文献2

:::info 在[1]的参考文献中， 文章 https://dml.cz/bitstream/handle/10338.dmlcz/102269/CzechMathJ_38-1988-4_18.pdf 给出了较为简单的紧嵌入定理 :::

区域由一系列性质较好的子区域去逼近，从而可以涵盖边界上有奇点的权，比如 .