题目链接
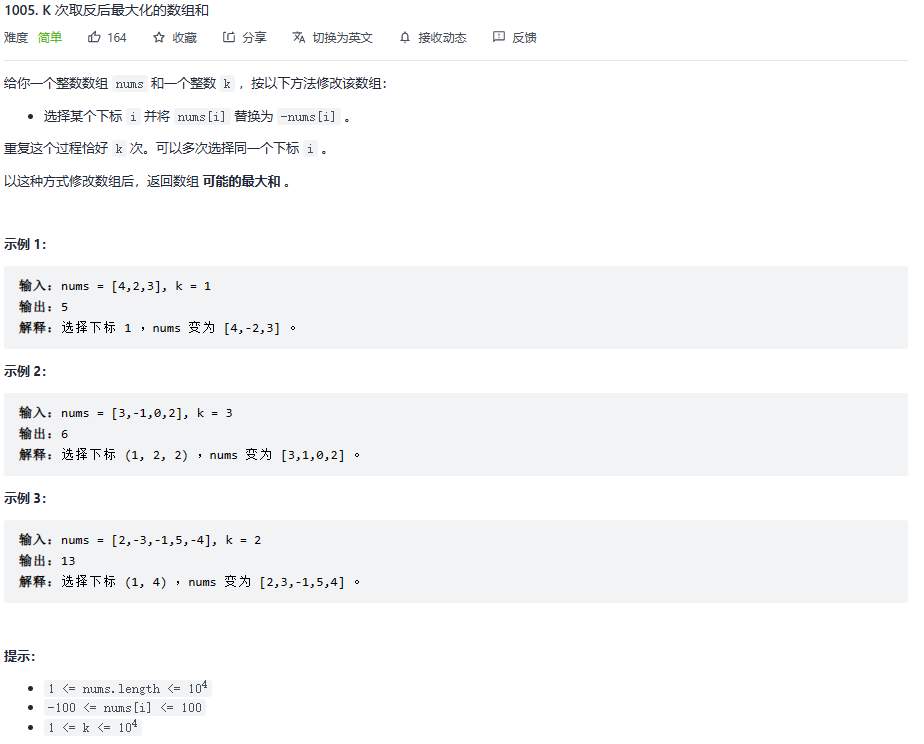
image.png

  1. /**
  2.  * @param {number[]} nums
  3.  * @param {number} k
  4.  * @return {number}
  5.  */
  7. const numsToNumber = (nums) => {
  8.   if (nums.length === 0) {
  9.     return 0;
  10.   }
  11.   return nums.reduce((prev, next) => {
  12.     return prev + next;
  13.   });
  14. };
  16. var largestSumAfterKNegations = function (nums, k) {
  17.   if (nums.length === 0) {
  18.     return 0;
  19.   }
  20.   nums.sort((prev, next) => {
  21.     return prev - next;
  22.   });
  24.   const l1 = nums.filter((num) => { return num < 0 }).sort((prev, next) => {
  25.     return prev - next;
  26.   });
  28.   const t = k % 2 === 0;
  29.   // 考虑无复数的情况
  30.   if (l1.length === 0 && t) {
  31.     return numsToNumber(nums);
  32.   } else if (l1.length === 0 && !t) {
  33.     return numsToNumber(nums) - 2 * nums[0];
  34.   }
  36.   // 到这里开始考虑数组内有负数的情况
  37.   const t2 = (k - l1.length) <= 0; //考虑k与负数个数的关系
  38.   if (t2) {
  39.     return numsToNumber(nums.filter((num) => { return num >= 0 })) - numsToNumber(l1.slice(0, k)) + numsToNumber(l1.slice(k, l1.length));
  40.   }
  41.   const t3 = (k - l1.length) % 2 === 0; //k > l1.length
  42.   // t3
  43.   if (t3) {
  44.     return numsToNumber(nums.map((num) => { return Math.abs(num) }));
  45.   }
  47.   const l2 = nums.map((num) => { return Math.abs(num) }).sort((prev, next) => {
  48.     return prev - next;
  49.   });
  50.   return numsToNumber(l2) - 2 * l2[0];
  53. };

思路：贪心算法

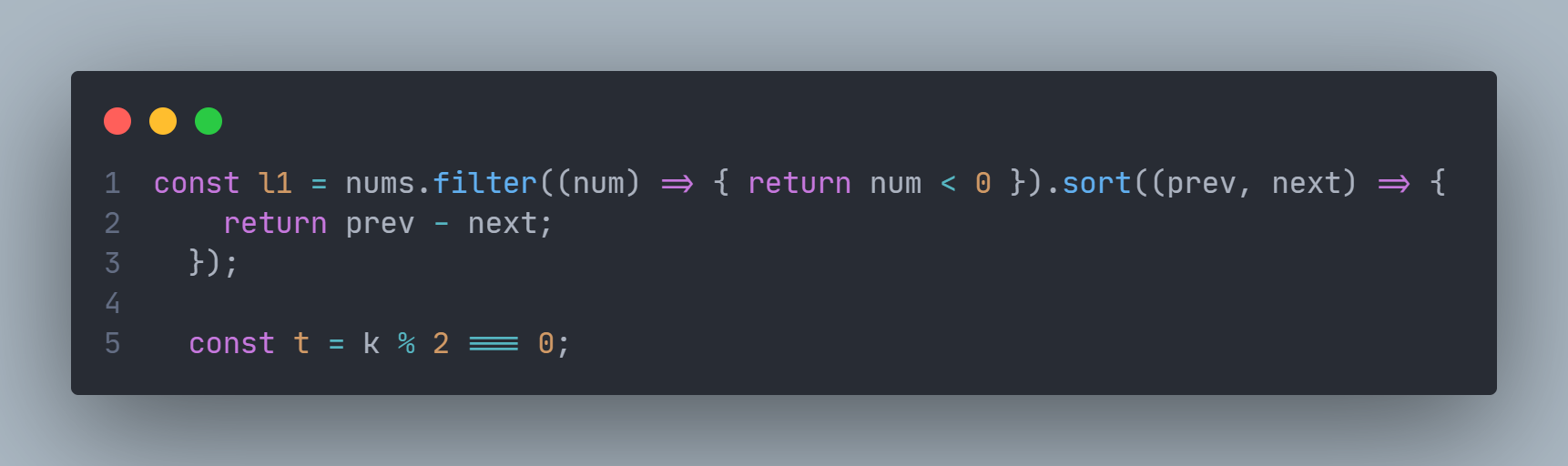
  1. 首先判断nums内有无负数(利用 l1 的长度来计算)以及k的奇偶性code01.png
  2. l1.length===0的情况下，如果k为偶数则自我抵消，对原数组无任何影响；若k为奇数则需要令nums的和减去两倍的nums中的最小值：code03.png
  3. 当l1.length>0时，我们首先考虑l1.length与k的差值大于等于0的特殊情况

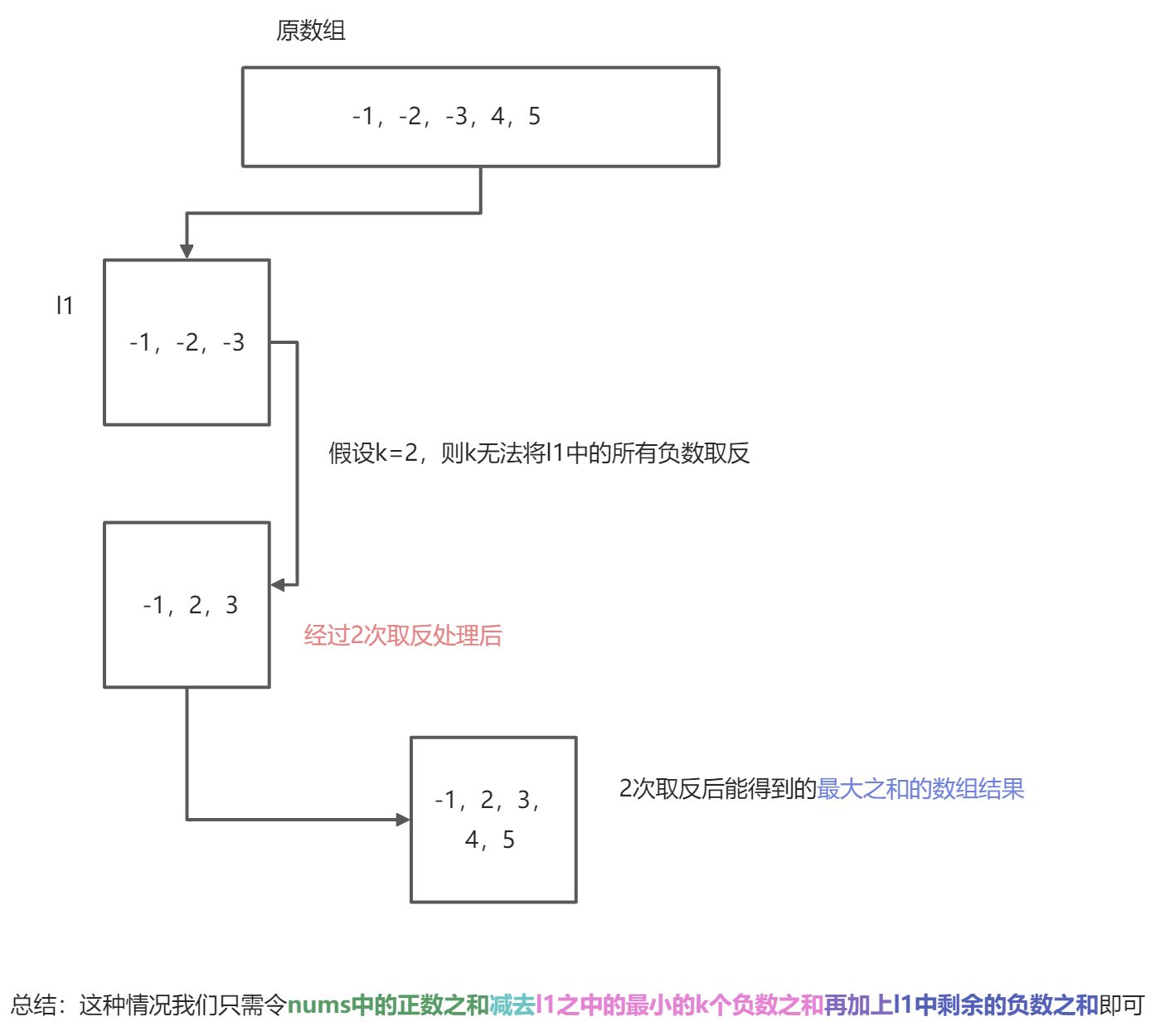
1005. K 次取反后最大化的数组和 - 图4
code02.png

  1. 接下来讨论l1.length < k的情况，此时如果(l1.length-k)%2===0,则k可以将l1中的负数全部取反，由于还会剩下偶数次取反的机会可以自我抵消（负负得正），因此我们只需要将nums全部取绝对值相加即可

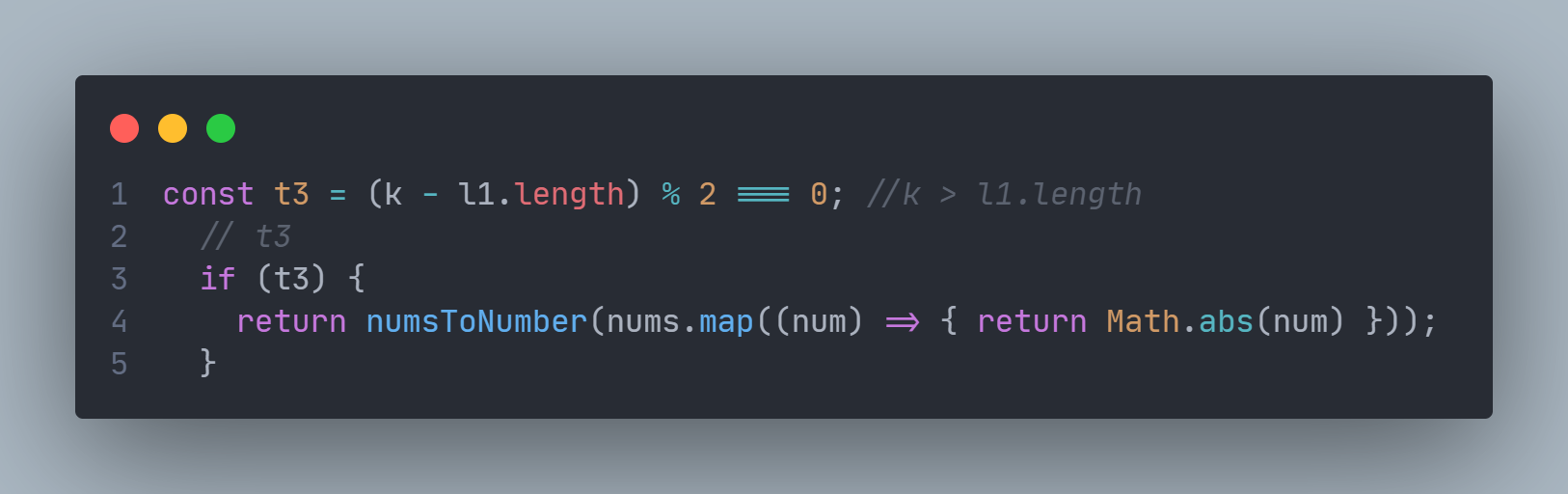
code04.png

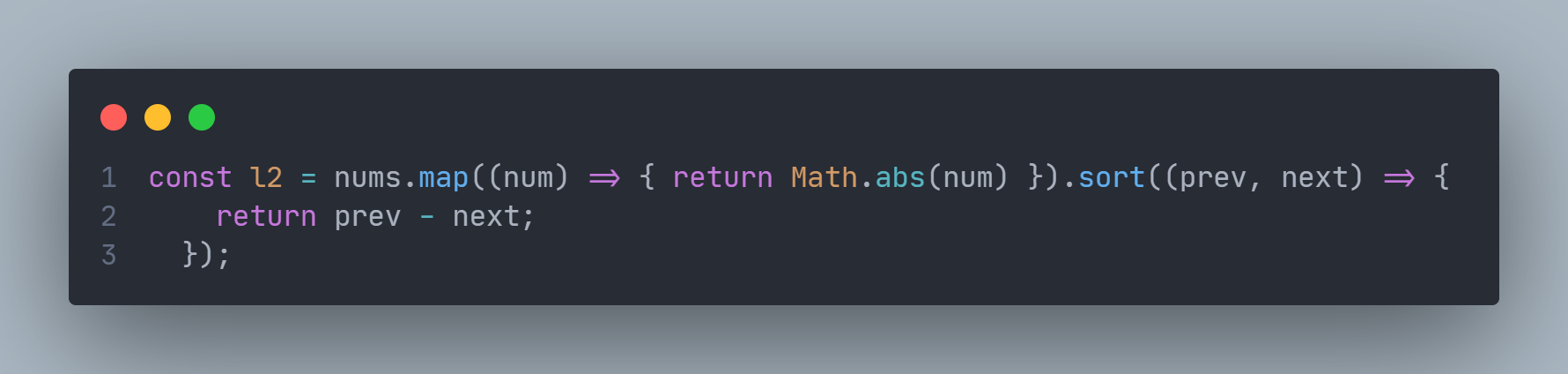
  1. 若l1.length < k且(l1.length-k)%2!==0，则首先： code05.png

由上可知l2是nums经过取绝对值并排序过后的数组，在这种情况下由于我们必须做出“牺牲”，令l2之中最小的值消耗完取反次数，则此时这个最小值会为负数，我们需要的结果就是l2的总和减去2倍的该最小值：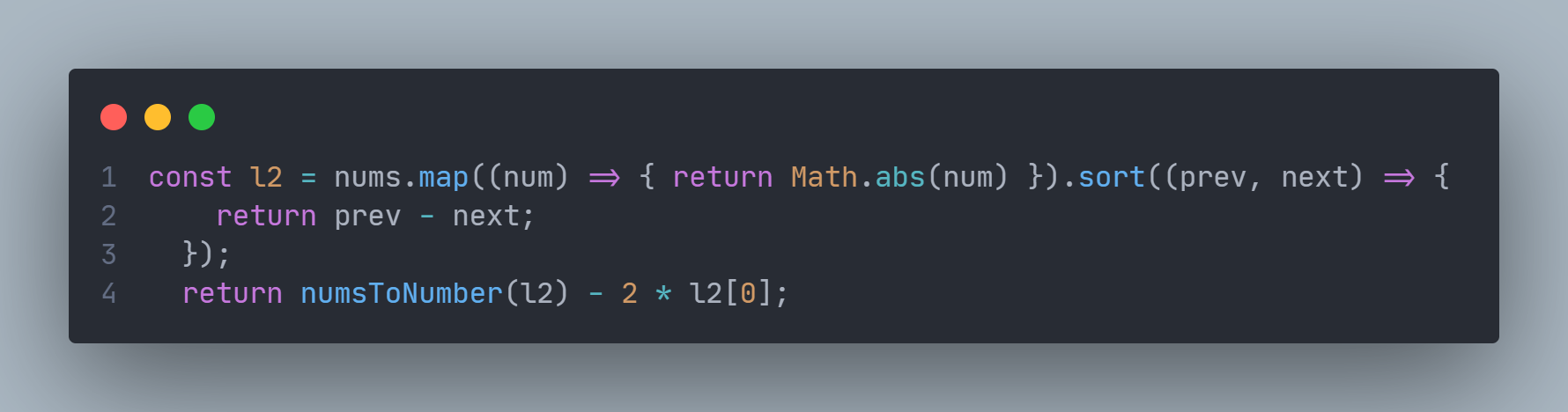
code06.png

ps.本人水平有限，欢迎批评指正