LeetCode：137. 只出现一次的数字 II

问题

https://leetcode-cn.com/problems/single-number-ii/

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现了三次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

示例 1:

输入: [2,2,3,2] 输出: 3 示例 2:

输入: [0,1,0,1,0,1,99]

输出: 99

思路

数值解法

数组中除某个元素外，其他的会出现 3 次，举个例子，给定数组：nums=[a, a, a, b, c, c, c]，那么有等式 3(a+b+c)=sum(nums)+2b，那么我们要的结果就是
b=(3(a+b+c)-sum(nums))/2

class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        return (3*sum(set(nums))-sum(nums))//2

逻辑电路

该思路源于作者：TankCode
来源：https://leetcode-cn.com/problems/single-number-ii/solution/luo-ji-dian-lu-jiao-du-xiang-xi-fen-xi-gai-ti-si-l/

这道题的引申义就是要让我们找到一种运算方式，使得 aaa=0 且 0a=a0=a， * 代表运算方式。

若读者学过数电的话，应该就会反映过来，这不就是类似于真值表找通式的过程吗？

1. 思路分析

• 第一时间应该想到的是找到一种逻辑操作，可以满足 1∗1∗1=0 且 0∗1=1∗0=1 ，其中 ∗ 为这种新逻辑操作符。根据这个，我们可以想到
  • 出现 0 次为 0，出现 1 次为 1，出现 2 次的值无所谓，出现 3 次就又回到 0，也就是说，我们一共需要记录 3 种状态：0 次，1 次，2 次，之后次数都是这三种状态的循环。其实这也就是一个模三运算。
    
  • 记录两个状态需要的是一位二进制 0/1，那么记录三种状态需要的是至少两位二进制，可以是 00, 01, 10, 11，这里我们只需要选其中任意三个状态即可，例如：00，01，10，分别代表 0 次 1 次 2 次。
    
  • 用 00 代表 0 次，01 代表出现 1 次是因为刚好对应数字原本那位上 0 代表 0 次，1 代表 1 次，这样可以方便写程序，不这么选也可以，但最后你自己要有个映射规则。至于 2 次的编码无所谓，10 和 11 都可以，反正最后答案也不要它，只是个中间状态，辅助我们计算的。
    
  • 那么对于输入数字的每一位二进制位，都可以用这三种状态表示。如果再输入一个数字，对于每一位上，我们的操作可以化为：
    • 新输入的是 0（即 00），三种状态都维持不变，00→00,01→01,10→10
      
    • 新输入的是 1（即 01），00→01,01→10,10→00

1. 求逻辑表达式

设当前状态为XY，输入为Z，那么我们可以分别为X 和Y列出真值表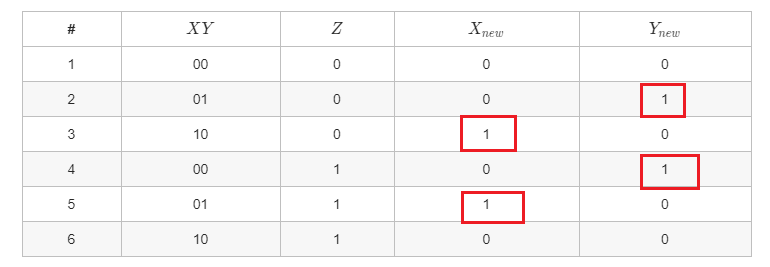

• 对于Y，转化为逻辑表达式就是（取所有的行的X,Y,Z 的最小项，然后OR 起来）

化简完就是

• 同理也可以得出X的逻辑表达式，但是这里有一个 tricky 的地方，不用再去求新的表达式。我们先更新完Y，然后把 放到逻辑表中替换原来Y的值形成新的逻辑表，这个逻辑表对X 来说是跟求Y 的时候的逻辑表是同构的。也就是说先更新Y以后，拿去更新X 时是可以直接套用刚才求的表达式的，也就是

• 这样就算做完了，把所有数以依次输入，然后不断更新这两个状态，最终，出现 3 次的位都成 0（也就是 00），出现 1 次的位都成了 1（也就是 01）。我们最后直接返回状态Y 就是要的答案。（另外辅助验证，最后X 应该为全 0，因为最后所有位的状态要么是 00，即出现 3 次的数的位，要么是 01，即出现 1 次的数的位）

代码

class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        X,Y=0,0
        for Z in nums:
            Y=Y^Z & ~X
            X=X^Z & ~Y
        return Y

而这个写法是上述介绍的直接用了去计算，可能有人这里不太明白，其实我们也可以 naive 地推出用旧Y 去计算 的表达式

class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        X,Y=0,0
        for Z in nums:
            Y_new=Y^Z & ~X
            X=(X&~Y&~Z)|(~X&Y&Z)
            Y=Y_new
        return Y

或者下面这个程序，原因是

class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        X = 0
        Y = 0
        for Z in nums:
            Y_new = ~X&(Y&~Z | ~Y&Z)
            X = (X&~Y&~Z | ~X&Y&Z)
            Y = Y_new
        return Y