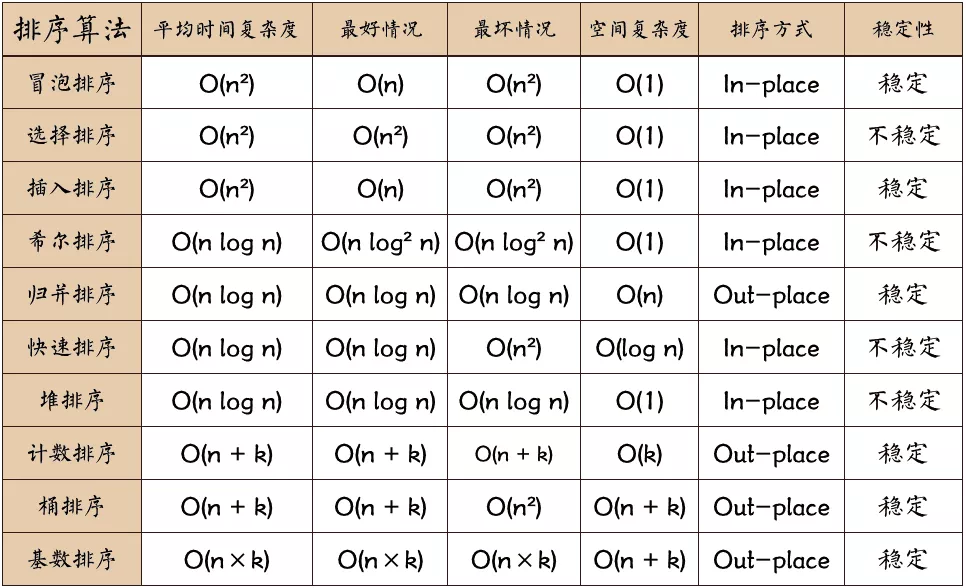
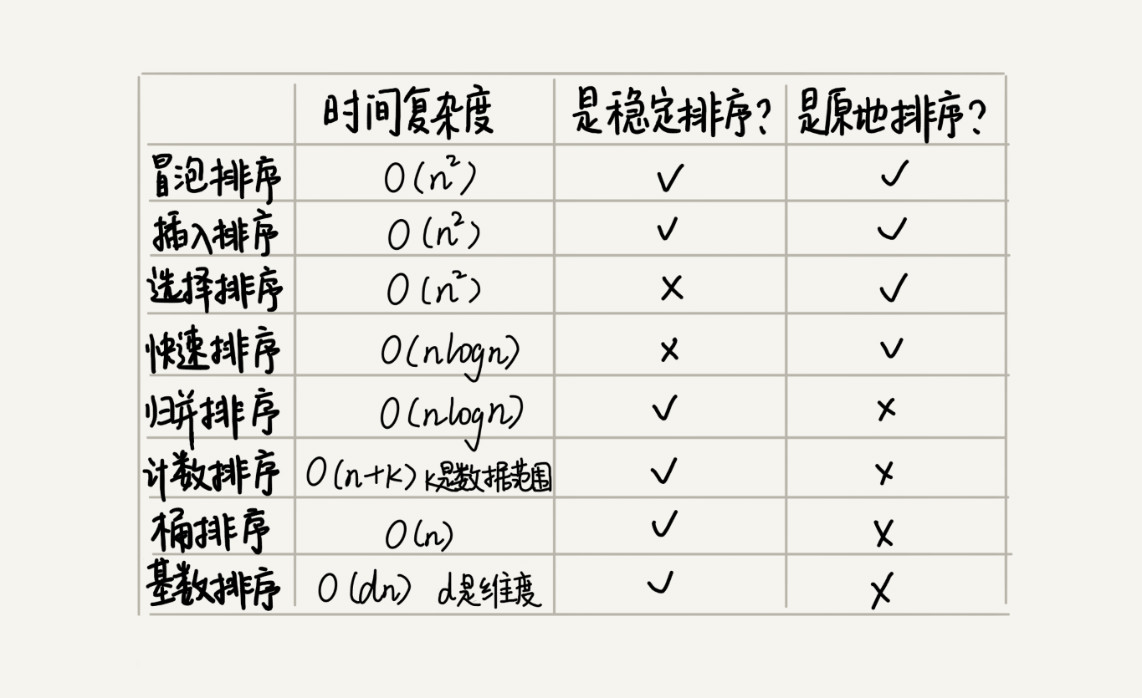
冒泡、插入、选择复杂度均为
快速排序、归并排序复杂度均为
选择，归并非稳定排序

冒泡排序、插入排序、选择排序这三种排序算法，它们的时间复杂度都是 ，比较高，适合小规模数据的排序。

动画可视化：https://visualgo.net/
该网站展示了一些常用算法的动画，帮助你形象的理解算法的含义

基本概念

排序算法的稳定性

如果待排序的序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序不变。

通过一个例子来解释一下。比如我们有一组数据 2，9，3，4，8，3，按照大小排序之后就是 2，3，3，4，8，9。这组数据里有两个 3。经过某种排序算法排序之后，如果两个 3 的前后顺序没有改变，那我们就把这种排序算法叫作稳定的排序算法；如果前后顺序发生变化，那对应的排序算法就叫作不稳定的排序算法。

1. 稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序。
2. 不是稳定的排序算法：选择排序、快速排序、希尔排序、堆排序。

“有序度” 和 “逆序度”

有序度是数组中具有有序关系的元素对的个数。

有序元素对：a[i] <= a[j], 如果 i < j。

同理，对于一个倒序排列的数组，比如 6，5，4，3，2，1，有序度是 0；对于一个完全有序的数组，比如 1，2，3，4，5，6，有序度就是 n*(n-1)/2，也就是 15。我们把这种完全有序的数组的有序度叫作满有序度。
**
逆序度的定义正好跟有序度相反（默认从小到大为有序）

逆序元素对：a[i] > a[j], 如果i < j。

逆序度 = 满有序度 - 有序度

排序的过程就是一种增加有序度，减少逆序度的过程，最后达到满有序度，就说明排序完成了。

举个例子：
要排序的数组的初始状态是 4，5，6，3，2，1 ，其中，有序元素对有 (4，5) (4，6)(5，6)，所以有序度是 3。n=6，所以排序完成之后终态的满有序度为 n*(n-1)/2=15。

冒泡排序包含两个操作原子，比较和交换。每交换一次，有序度就加 1。不管算法怎么改进，交换次数总是确定的，即为逆序度，也就是 n*(n-1)/2–初始有序度。此例中就是 15–3=12，要进行 12 次交换操作。

排序算法的执行效率

• 最好情况、最坏情况、平均情况时间复杂度

我们在分析排序算法的时间复杂度时，要分别给出最好情况、最坏情况、平均情况下的时间复杂度。除此之外，你还要说出最好、最坏时间复杂度对应的要排序的原始数据是什么样的。

为什么要区分这三种时间复杂度呢？第一，有些排序算法会区分，为了好对比，所以我们最好都做一下区分。第二，对于要排序的数据，有的接近有序，有的完全无序。有序度不同的数据，对于排序的执行时间肯定是有影响的，我们要知道排序算法在不同数据下的性能表现。

• 时间复杂度的系数、常数 、低阶

我们知道，时间复杂度反应的是数据规模 n 很大的时候的一个增长趋势，所以它表示的时候会忽略系数、常数、低阶。但是实际的软件开发中，我们排序的可能是 10 个、100 个、1000 个这样规模很小的数据，所以，在对同一阶时间复杂度的排序算法性能对比的时候，我们就要把系数、常数、低阶也考虑进来。

• 比较次数和交换（或移动）次数

基于比较的排序算法。基于比较的排序算法的执行过程，会涉及两种操作，一种是元素比较大小，另一种是元素交换或移动。所以，如果我们在分析排序算法的执行效率的时候，应该把比较次数和交换（或移动）次数也考虑进去。

排序算法的内存消耗

原地排序（Sorted in place）。原地排序算法，就是特指空间复杂度是 O(1) 的排序算法。

排序算法汇总

冒泡排序

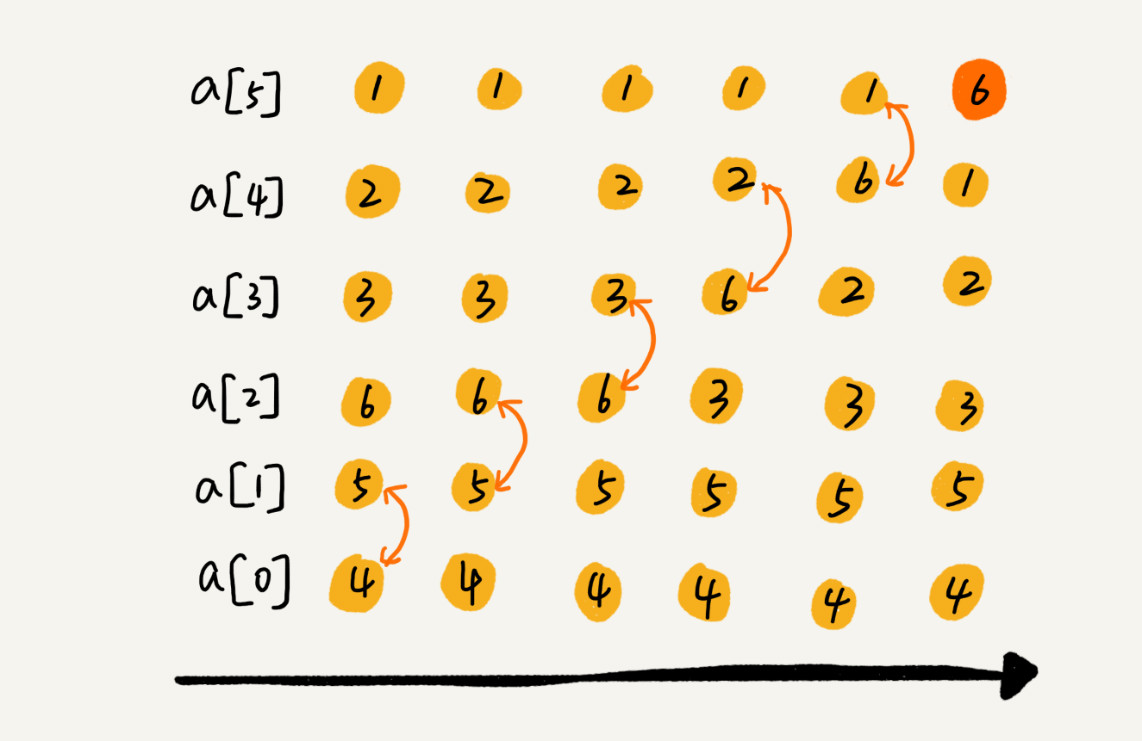
• 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
  
• 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数（如上面的 6 ）。
  
• 针对所有的元素重复以上的步骤，除了最后一个。
  
• 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

当某次冒泡操作已经没有数据交换时，说明已经达到完全有序，不用再继续执行后续的冒泡操作。我这里还有另外一个例子，这里面给 6 个元素排序，只需要 4 次冒泡操作就可以了。

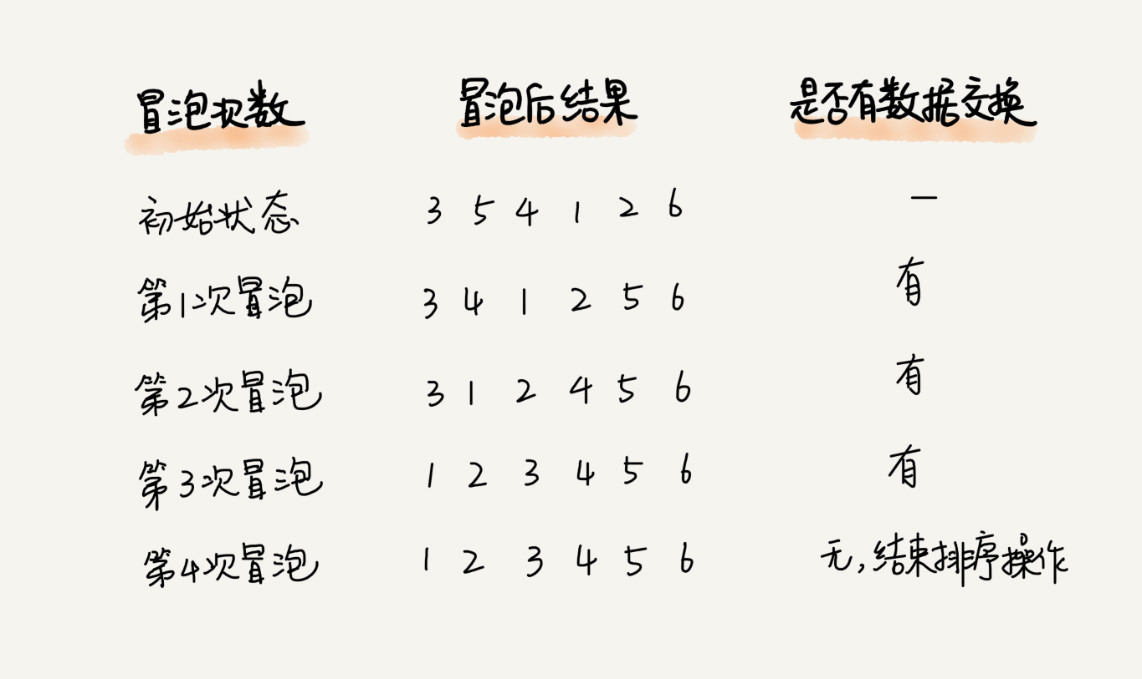
注：如果已经是排序好了的，就没有必要再遍历一遍了，所以设置了一个标注位，判断是否排序完成

代码

注意点：

def BubbleSort(array):
    length = len(array)
    for i in range(1, length): # 大循环比较次数
        flag = True # 一个标志位，判断是否排序完成
        for j in range(length-i): # 小循环比较次数
            if array[j] > array[j+1]:
                array[j], array[j+1] = array[j+1], array[j]
                flag = False
        if flag:
            break
    return array

复杂度

• 最好情况时间复杂度是 O (n)，完全有序，检查一遍即可
• 最坏的情况是，要排序的数据刚好是倒序排列的，我们需要进行 n 次冒泡操作，所以最坏情况时间复杂度为 O (n2)。
• 平均复杂度 O (n2)

冒泡的过程只涉及相邻数据的交换操作，只需要常量级的临时空间，所以它的空间复杂度为 O (1)，是一个原地排序算法。

在冒泡排序中，只有交换才可以改变两个元素的前后顺序。为了保证冒泡排序算法的稳定性，当有相邻的两个元素大小相等的时候，我们不做交换，相同大小的数据在排序前后不会改变顺序，所以冒泡排序是稳定的排序算法。

插入排序（最常用）

• 将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。
• 从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）

def InsertSort(array):        
    length = len(array)
    if length < 2:
        return array
    sorted_num = 1 # 已经排序的数量，第一次是数组中的第一个
    for i in range(sorted_num, length): # 对未排序的序列进行遍历
        for j in range(sorted_num): # 遍历已排序的序列
            if array[i] < array[j]: # 未排序的序列中的每个元素与已经排序的每个元素进行对比
                array[i], array[j] = array[j], array[i]
        sorted_num += 1 # 排序一个就在已排序的序列中加 1
    return array

从实现过程可以很明显地看出，插入排序算法的运行并不需要额外的存储空间，所以空间复杂度是 O (1)，也就是说，这是一个原地排序算法。

在插入排序中，对于值相同的元素，我们可以选择将后面出现的元素，插入到前面出现元素的后面，这样就可以保持原有的前后顺序不变，所以插入排序是稳定的排序算法。

选择排序

• 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
  
• 再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
  
• 重复第二步，直到所有元素均排序完毕。

def SelectionSort(array):
      length = len(array)
      for i in range(length-1): # 需要比较的轮次
        min_index = i
        for j in range(i+1, length): # 每次需要比较的次数，去掉已经排好序的
          if array[j] > array[min_index]:
            min_index = j
        if i != min_index: # 如果最小值的索引与当前值的索引不同，则交换
          array[i], array[min_index] = array[min_index], array[i]
      return array

不稳定算法、原地排序

归并排序（Merge Sort）

归并排序的核心思想还是蛮简单的。如果要排序一个数组，我们先把数组从中间分成前后两部分，然后对前后两部分分别排序，再将排好序的两部分合并在一起，这样整个数组就都有序了。

归并排序使用的就是分治思想。分治，顾名思义，就是分而治之，将一个大问题分解成小的子问题来解决。小的子问题解决了，大问题也就解决了。

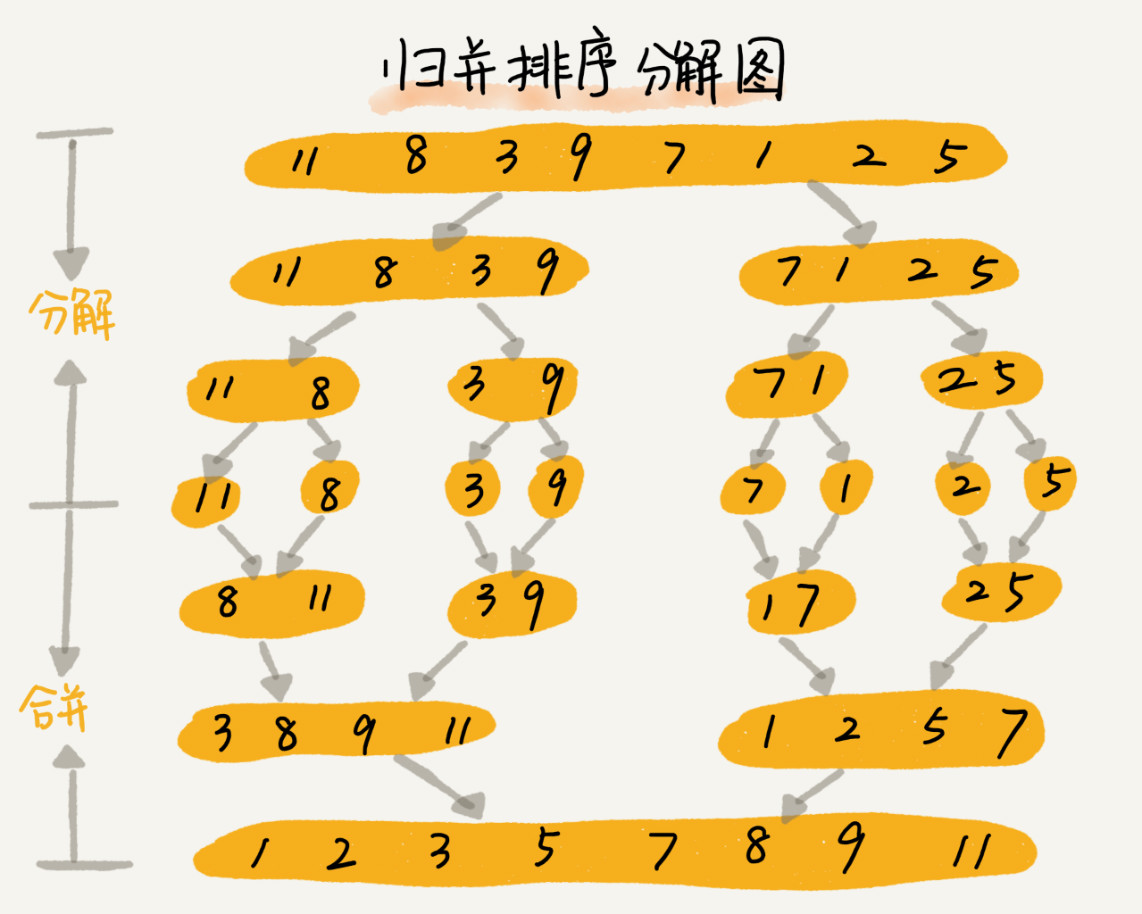
合并过程：

class merge_sorted():
    def sort(self, array):
        """
        排序
        """
        length = len(array)
        if length < 2:
            return array
        mid = length // 2
        left = array[:mid]
        right = array[mid:]
        return self.merge(self.sort(left), self.sort(right)) # 两部分排序后合并


    def merge(self, left, right):
        """
        合并两个排序的数组
        """ 
        result = [0]*(len(left)+len(right)) # 创建一个新数组

        # 依次比较两个数组的元素
        i = 0
        while len(left) > 0 and len(right) > 0:
            if left[0] <= right[0]:
                result[i] = left[0]
                i += 1
                left = left[1:]
            else:
                result[i] = right[0]
                i += 1                
                right = right[1:]
        # 如果 left 数组还有剩余的话        
        while len(left) > 0:
            result[i] = left[0]
            i += 1
            left = left[1:]

        # 如果 right 数组还有剩余的话
        while len(right) > 0:
            result[i] = right[0]
            i += 1                
            right = right[1:]

        return result

array = [5, 3, 4, 1, 2, 7, 1]    
s = merge_sorted()
s.sort(array)

归并排序是一个稳定的排序算法。

归并排序的执行效率与要排序的原始数组的有序程度无关，所以其时间复杂度是非常稳定的，不管是最好情况、最坏情况，还是平均情况，时间复杂度都是 O(nlogn)。

尽管每次合并操作都需要申请额外的内存空间，但在合并完成之后，临时开辟的内存空间就被释放掉了。在任意时刻，CPU 只会有一个函数在执行，也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超过 n 个数据的大小，所以空间复杂度是 O(n)。归并排序不是原地排序算法。

快速排序算法（Quicksort）

算法思想

如果要排序数组中下标从 p 到 r 之间的一组数据，我们选择 p 到 r 之间的任意一个数据作为 pivot（分区点）。

我们遍历 p 到 r 之间的数据，将小于 pivot 的放到左边，将大于 pivot 的放到右边，将 pivot 放到中间。经过这一步骤之后，数组 p 到 r 之间的数据就被分成了三个部分，前面 p 到 q-1 之间都是小于 pivot 的，中间是 pivot，后面的 q+1 到 r 之间是大于 pivot 的。

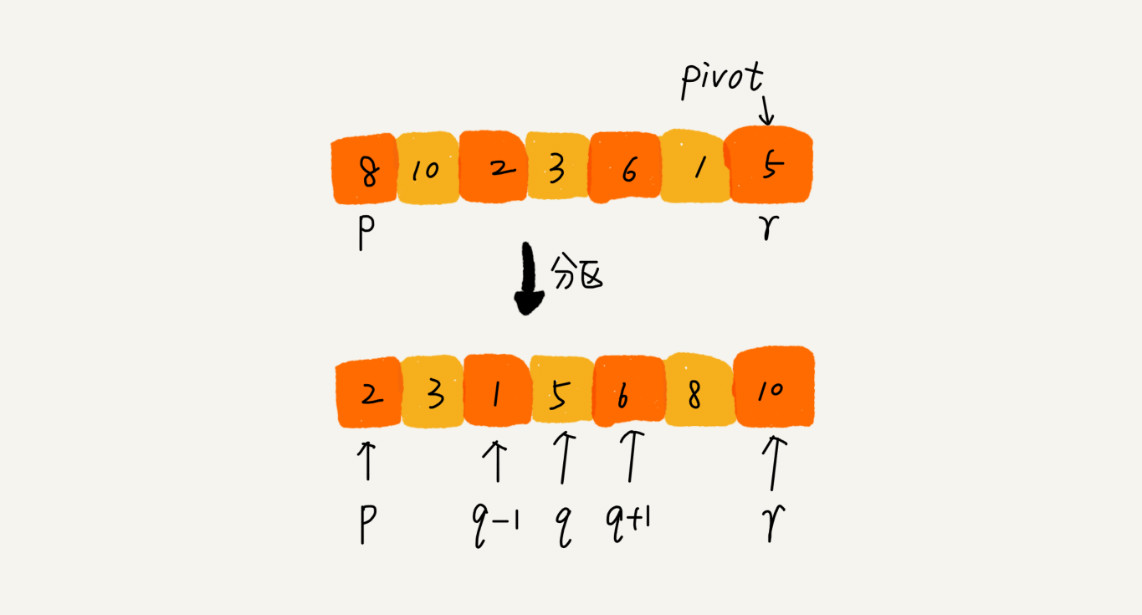
根据分治、递归的处理思想，我们可以用递归排序下标从 p 到 q-1 之间的数据和下标从 q+1 到 r 之间的数据，直到区间缩小为 1，就说明所有的数据都有序了。

分区（选择最后一个元素作为分区点）

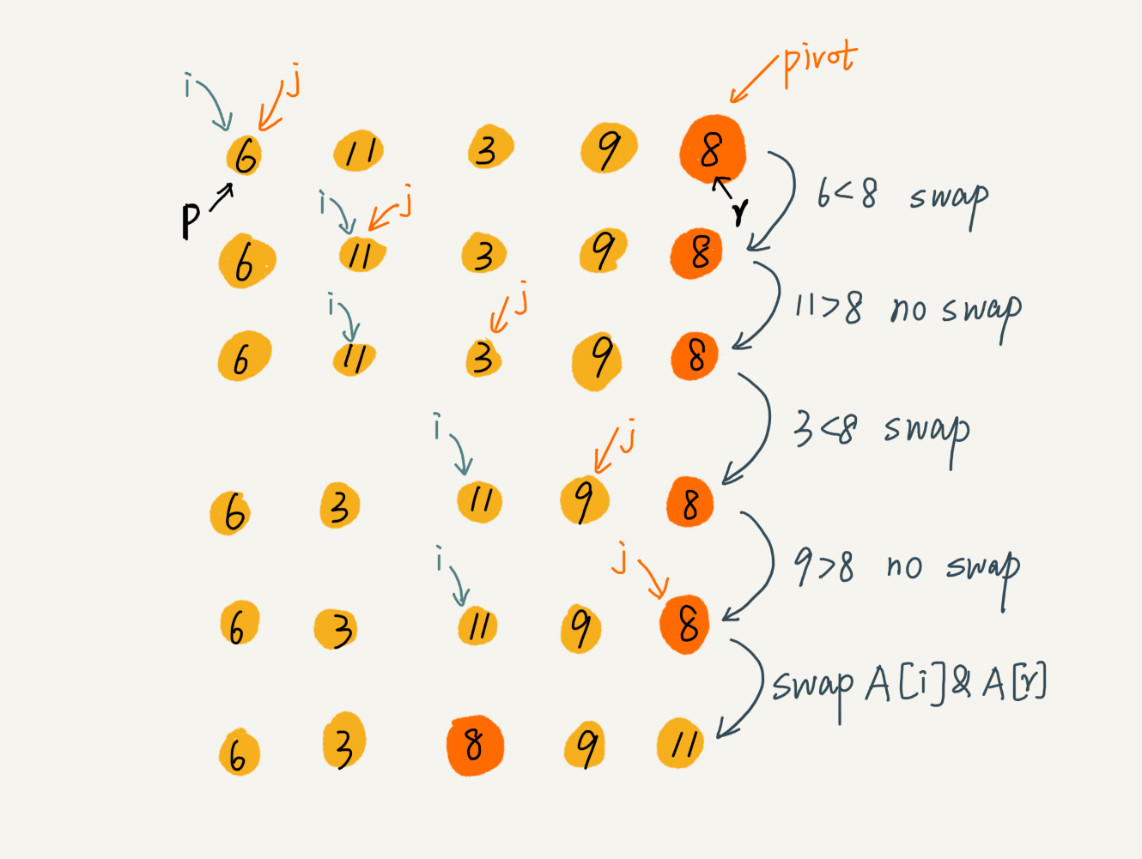
from typing import List
import random


def quick_sort(a: List[int]):
    _quick_sort_between(a, 0, len(a) - 1)


def _quick_sort_between(a: List[int], low: int, high: int):
    """
    low 是 a 的最低索引
    high 是 a 的最高索引
    """
    if low < high:
        m = _partition(a, low, high)  # a[m] is in final position
        _quick_sort_between(a, low, m - 1)
        _quick_sort_between(a, m + 1, high)


def _partition(a: List[int], low: int, high: int):
    """
    low 是 a 的最低索引
    high 是 a 的最高索引
    返回分区好的分区值的索引
    """
    pivot = a[high] # 选取最后一个元素作为分区值
    i = low
    for j in range(low, high): # 从头遍历到倒数第二个元素
        if a[j] < pivot: # 
            a[j], a[i] = a[i], a[j]  # swap
            i += 1
    a[i], a[high] = a[high], a[i]
    return i

快排的时间复杂度也是 O (nlogn)。

快速排序优化

时间复杂度优化和函数栈优化

• 时间复杂度退化的例子

比如 1，3，5，6，8。如果我们每次选择最后一个元素作为 pivot，那每次分区得到的两个区间都是不均等的。我们需要进行大约 n 次分区操作，才能完成快排的整个过程。每次分区我们平均要扫描大约 n/2 个元素，这种情况下，快排的时间复杂度就从 O(nlogn) 退化成了 O(n2)。

如果数据原来就是有序的或者接近有序的，每次分区点都选择最后一个数据，那快速排序算法就会变得非常糟糕，时间复杂度就会退化为 O(n2)。实际上，这种 O(n2) 时间复杂度出现的主要原因还是因为我们分区点选的不够合理。

最理想的分区点是：被分区点分开的两个分区中，数据的数量差不多。

• 分区算法
  • 三数取中法

    我们从区间的首、尾、中间，分别取出一个数，然后对比大小，取这 3 个数的中间值作为分区点。这样每间隔某个固定的长度，取数据出来比较，将中间值作为分区点的分区算法，肯定要比单纯取某一个数据更好。但是，如果要排序的数组比较大，那 “三数取中” 可能就不够了，可能要 “五数取中” 或者 “十数取中”。

• 随机法

  随机法就是每次从要排序的区间中，随机选择一个元素作为分区点。这种方法并不能保证每次分区点都选的比较好，但是从概率的角度来看，也s不大可能会出现每次分区点都选的很差的情况，所以平均情况下，这样选的分区点是比较好的。时间复杂度退化为最糟糕的 O(n2) 的情况，出现的可能性不大。

归并排序与快速排序的区别

快排和归并用的都是分治思想，递推公式和递归代码也非常相似，那它们的区别在哪里呢？

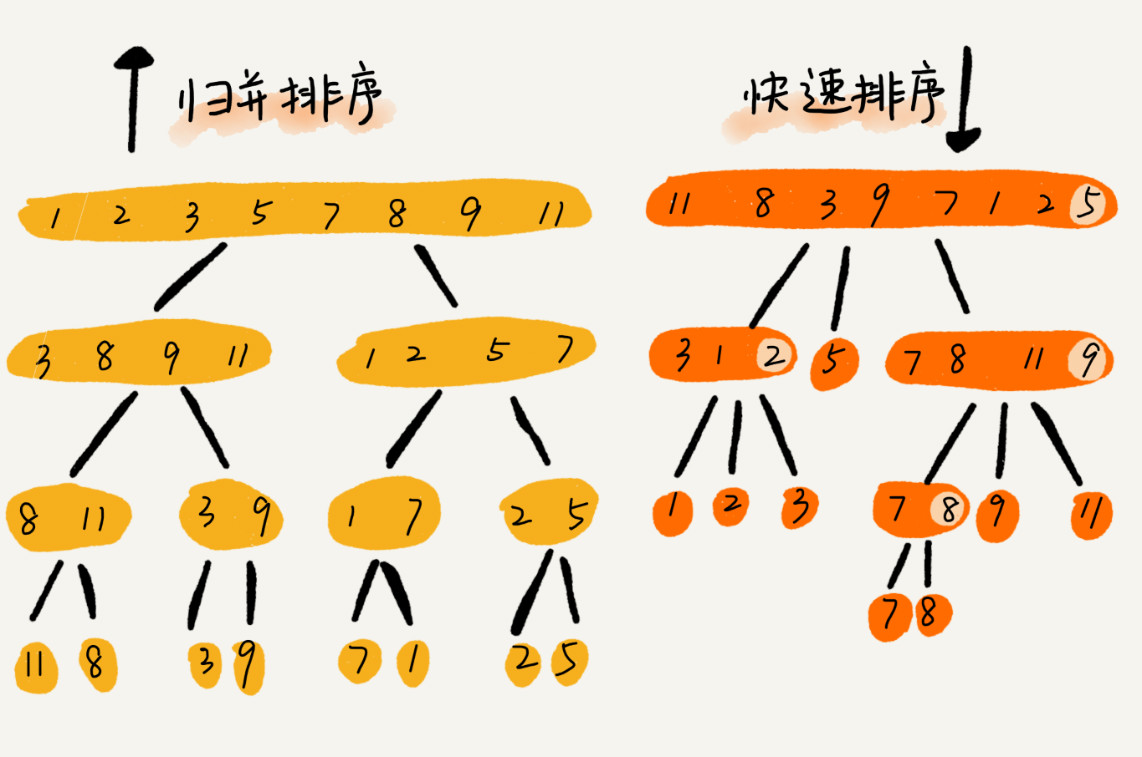
可以发现，归并排序的处理过程是由下到上的，先处理子问题，然后再合并。而快排正好相反，它的处理过程是由上到下的，先分区，然后再处理子问题。归并排序虽然是稳定的、时间复杂度为 O (nlogn) 的排序算法，但是它是非原地排序算法。我们前面讲过，归并之所以是非原地排序算法，主要原因是合并函数无法在原地执行。快速排序通过设计巧妙的原地分区函数，可以实现原地排序，解决了归并排序占用太多内存的问题。

桶排序『Bucket sort』（时间复杂度是线性的）

时间复杂度分析

如果要排序的数据有 n 个，我们把它们均匀地划分到 m 个桶内，每个桶里就有 k=n/m 个元素。每个桶内部使用快速排序，时间复杂度为 O (k logk)。m 个桶排序的时间复杂度就是 O (m k logk)，因为 k=n/m，所以整个桶排序的时间复杂度就是 O (nlog (n/m))。当桶的个数 m 接近数据个数 n 时，log (n/m) 就是一个非常小的常量，这个时候桶排序的时间复杂度接近 O (n)。

适用场景

桶排序比较适合用在外部排序中。所谓的外部排序就是数据存储在外部磁盘中，数据量比较大，内存有限，无法将数据全部加载到内存中。

可以多次进行分桶

计数排序『Counting sort』（时间复杂度是线性的）

举个例子

假设只有 8 个考生，分数在 0 到 5 分之间。这 8 个考生的成绩我们放在一个数组 A [8] 中，它们分别是：2，5，3，0，2，3，0，3。

考生的成绩从 0 到 5 分，我们使用大小为 6 的数组 C [6] 表示桶，其中下标对应分数。不过，C [6] 内存储的并不是考生，而是对应的考生个数。像我刚刚举的那个例子，我们只需要遍历一遍考生分数，就可以得到 C [6] 的值。

从图中可以看出，分数为 3 分的考生有 3 个，小于 3 分的考生有 4 个，所以，成绩为 3 分的考生在排序之后的有序数组 R [8] 中，会保存下标 4，5，6 的位置。

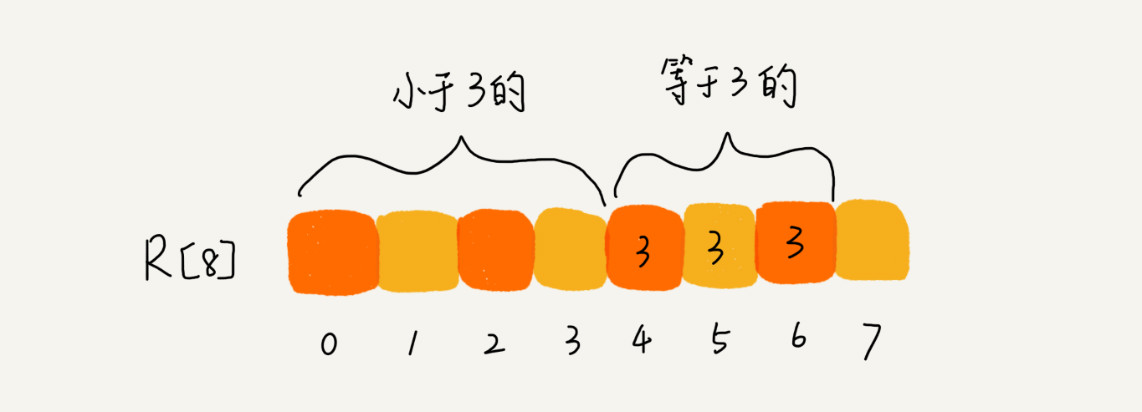
那我们如何快速计算出，每个分数的考生在有序数组中对应的存储位置呢？这个处理方法非常巧妙，很不容易想到。

思路是这样的：我们对 C [6] 数组顺序求和，C [6] 存储的数据就变成了下面这样
子。C [k] 里存储小于等于分数 k 的考生个数。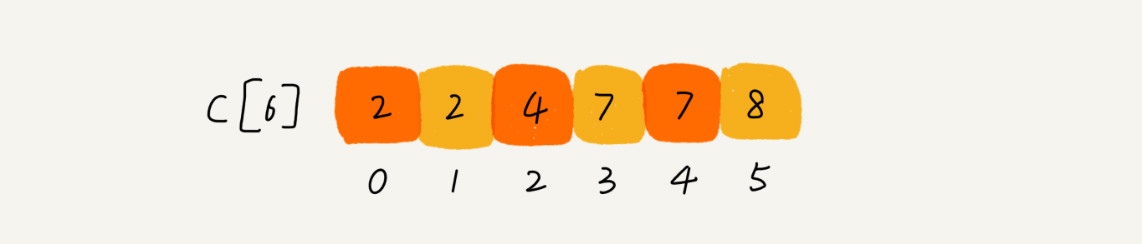

有了前面的数据准备之后，现在我就要讲计数排序中最复杂、最难理解的一部分了，请集中精力跟着我的思路！

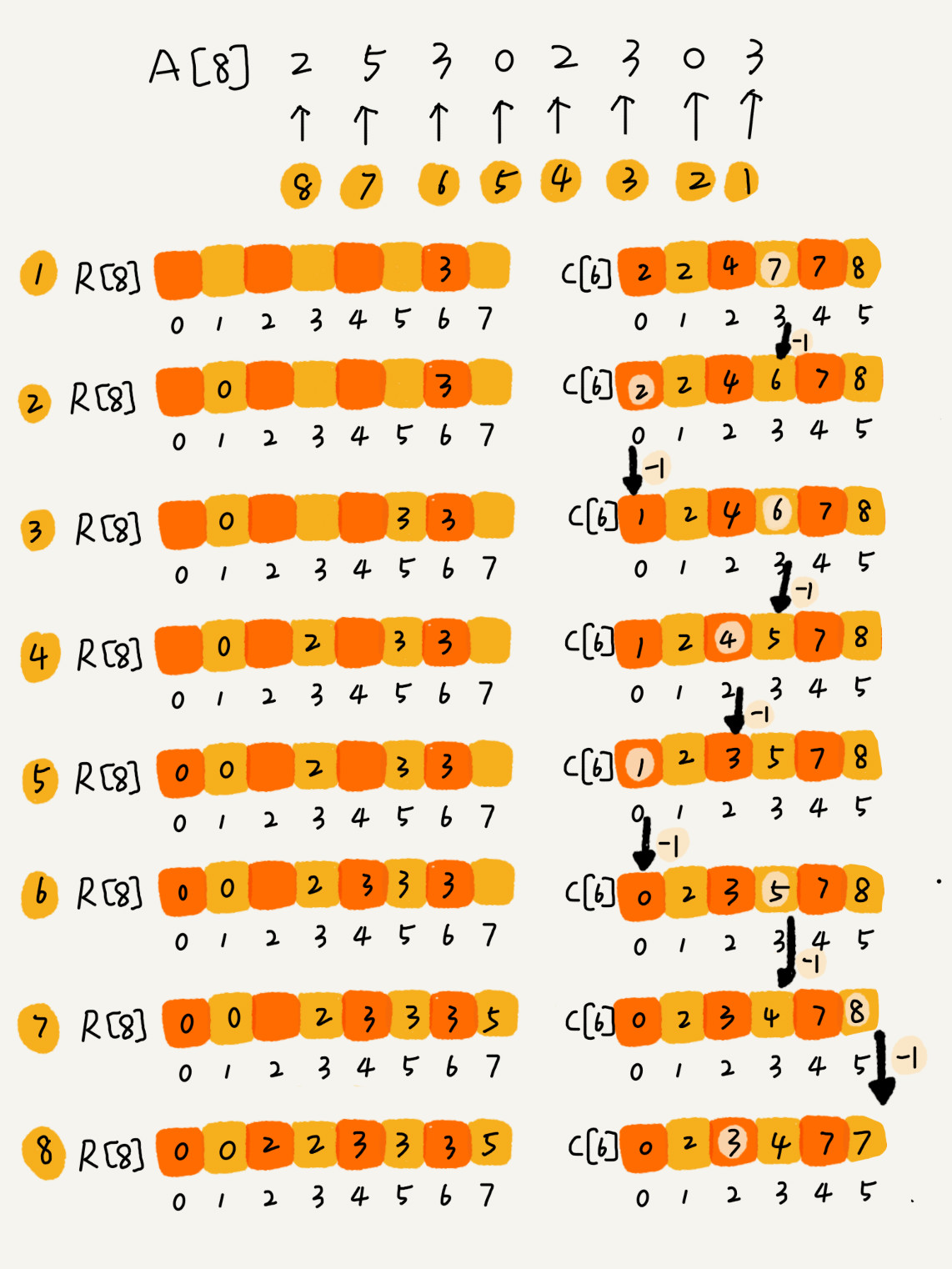
我们从后到前依次扫描数组 A（原始数组）。比如，当扫描到 3 时，我们可以从数组 C 中取出下标为 3 的值 7，也就是说，到目前为止，包括自己在内，分数小于等于 3 的考生有 7 个，也就是说 3 是数组 R 中的第 7 个元素（也就是数组 R 中下标为 6 的位置）。当 3 放入到数组 R 中后，小于等于 3 的元素就只剩下了 6 个了，所以相应的 C [3] 要减 1，变成 6。

以此类推，当我们扫描到第 2 个分数为 3 的考生的时候，就会把它放入数组 R 中的第 6 个元素的位置（也就是下标为 5 的位置）。当我们扫描完整个数组 A 后，数组 R 内的数据就是按照分数从小到大有序排列的了。

使用场景

计数排序只能用在数据范围不大的场景中，如果数据范围 k 比要排序的数据 n 大很多，就不适合用计数排序了。而且，计数排序只能给非负整数排序，如果要排序的数据是其他类型的，要将其在不改变相对大小的情况下，转化为非负整数。

比如，还是拿考生这个例子。如果考生成绩精确到小数后一位，我们就需要将所有的分数都先乘以 10，转化成整数，然后再放到 9010 个桶内。再比如，如果要排序的数据中有负数，数据的范围是 [-1000, 1000]，那我们就需要先对每个数据都加 1000，转化成非负整数。

代码

def counting_sort(a):
    # 创建结果数组
    result = [None]*len(a)

    # 找出数组中最大的值
    max_val = max(a)

    # 创建一个计数数组 c
    c = [0]*(max_val+1)

    # 遍历数组 a，统计所有元素的个数，对应索引加 1
    for i in a:
        c[i] += 1

    # 对计数数组顺序累加
    for i in range(1, max_val+1):
        c[i] = c[i] + c[i-1]
#     print(c)

    # 从后往前遍历原始数组 a
    for i in a[::-1]:
        index = i
        c[index] -= 1
        result[c[index]] = index
    return result

基数排序『Radix sort』（时间复杂度是线性的）

我们再来看这样一个排序问题。假设我们有 10 万个手机号码，希望将这 10 万个手机号码从小到大排序，你有什么比较快速的排序方法呢？

快排，时间复杂度可以做到 O(nlogn)，还有更高效的排序算法吗？桶排序、计数排序能派上用场吗？手机号码有 11 位，范围太大，显然不适合用这两种排序算法。针对这个排序问题，有没有时间复杂度是 O (n) 的算法呢？现在我就来介绍一种新的排序算法，基数排序。

刚刚这个问题里有这样的规律：假设要比较两个手机号码 a，b 的大小，如果在前面几位中，a 手机号码已经比 b 手机号码大了，那后面的几位就不用看了。

借助稳定排序算法，这里有一个巧妙的实现思路。 先按照最后一位来排序手机号码，然后，再按照倒数第二位重新排序，以此类推，最后按照第一位重新排序。经过 11 次排序之后，手机号码就都有序了。

手机号码稍微有点长，画图比较不容易看清楚，我用字符串排序的例子，画了一张基数排序的过程分解图，你可以看下。

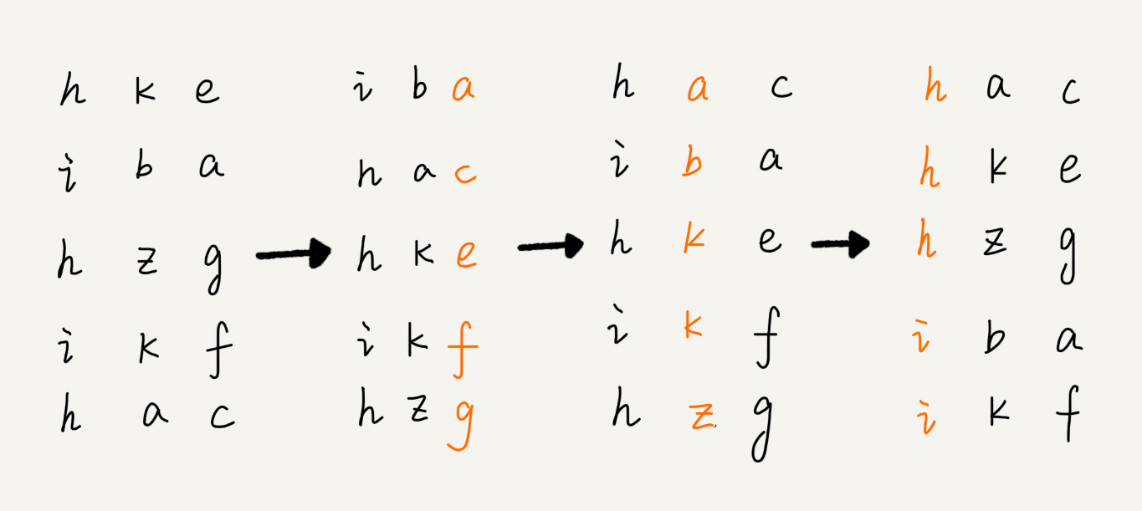
注意，这里按照每位来排序的排序算法要是稳定的，否则这个实现思路就是不正确的。因为如果是非稳定排序算法，那最后一次排序只会考虑最高位的大小顺序，完全不管其他位的大小关系，那么低位的排序就完全没有意义了。

根据每一位来排序，我们可以用刚讲过的桶排序或者计数排序，它们的时间复杂度可以做到 O (n)。如果要排序的数据有 k 位，那我们就需要 k 次桶排序或者计数排序，总的时间复杂度是 O (k*n)。当 k 不大的时候，比如手机号码排序的例子，k 最大就是 11，所以基数排序的时间复杂度就近似于 O (n)。

实际上，有时候要排序的数据并不都是等长的，比如我们排序牛津字典中的 20 万个英文单词，最短的只有 1 个字母，最长的我特意去查了下，有 45 个字母，中文翻译是尘肺病。对于这种不等长的数据，基数排序还适用吗？

实际上，我们可以把所有的单词补齐到相同长度，位数不够的可以在后面补 “0”，因为根据 ASCII 值，所有字母都大于 “0”，所以补 “0” 不会影响到原有的大小顺序。这样就可以继续用基数排序了。我来总结一下，基数排序对要排序的数据是有要求的，需要可以分割出独立的 “位” 来比较，而且位之间有递进的关系，如果 a 数据的高位比 b

基数排序对要排序的数据是有要求的，需要可以分割出独立的 “位” 来比较，而且位之间有递进的关系，如果 a 数据的高位比 b 数据大，那剩下的低位就不用比较了。除此之外，每一位的数据范围不能太大，要可以用线性排序算法来排序，否则，基数排序的时间复杂度就无法做到 O(n) 了。

参考

• https://mp.weixin.qq.com/s/vn3KiV-ez79FmbZ36SX9lg