数据结构 - 栈（stack） - 《数据结构与算法学习之路》

栈的理解
基本操作和使用场景
栈的几个应用场景
相关题目

栈的理解

后进者先出，先进者后出，这就是典型的 “栈” 结构。
形象比喻：叠盘子

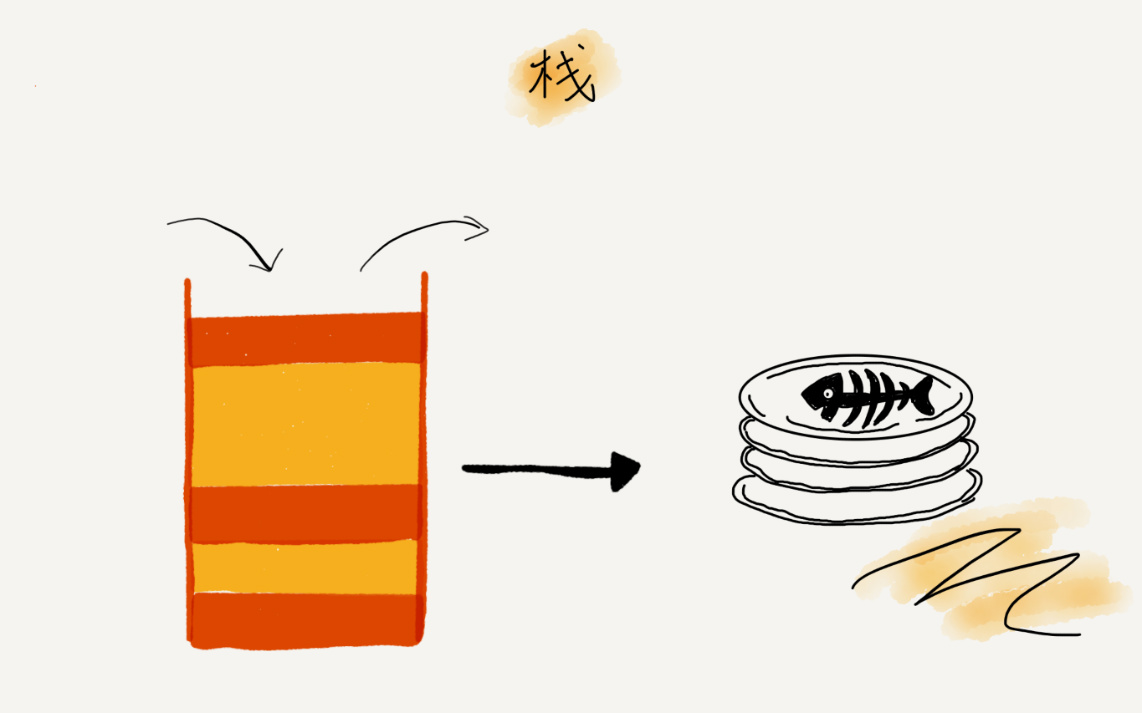
栈（stack） - 图1

基本操作和使用场景

基本操作

入栈和出栈，也就是在栈顶插入一个数据和从栈顶删除一个数据。

栈既可以用数组来实现，也可以用链表来实现。用数组实现的栈，我们叫作顺序栈，用链表实现的栈，我们叫作链式栈。

"""
    Stack based upon linked list
    基于链表实现的栈
    Author: Wenru
"""
from typing import Optional
class Node:
    def __init__(self, data: int, next=None):
        self._data = data
        self._next = next
class LinkedStack:
    """A stack based upon singly-linked list.
    """
    def __init__(self):
        self._top: Node = None
    def push(self, value: int):
        new_top = Node(value)
        new_top._next = self._top
        self._top = new_top
    def pop(self) -> Optional[int]:
        if self._top:
            value = self._top._data
            self._top = self._top._next
            return value
    def __repr__(self) -> str:
        current = self._top
        nums = []
        while current:
            nums.append(current._data)
            current = current._next
        return " ".join(f"{num}]" for num in nums)
if __name__ == "__main__":
    stack = LinkedStack()
    for i in range(9):
        stack.push(i)
    print(stack)
    for _ in range(3):
        stack.pop()
    print(stack)

复杂度分析

不管是顺序栈还是链式栈，我们存储数据只需要一个大小为 n 的数组就够了。在入栈和出栈过程中，只需要一两个临时变量存储空间，所以空间复杂度是 O(1)。

注意，这里存储数据需要一个大小为 n 的数组，并不是说空间复杂度就是 O(n)。因为，这 n 个空间是必须的，无法省掉。所以我们说空间复杂度的时候，是指除了原本的数据存储空间外，算法运行还需要额外的存储空间。

时间复杂度也不难。不管是顺序栈还是链式栈，入栈、出栈只涉及栈顶个别数据的操作，所以时间复杂度都是 O (1)。

使用场景

当某个数据集合只涉及在一端插入和删除数据，并且满足后进先出、先进后出的特性，我们就应该首选 “栈” 这种数据结构。

栈的几个应用场景

函数调用


int main() {
   int a = 1; 
   int ret = 0;
   int res = 0;
   ret = add(3, 5);
   res = a + ret;
   printf("%d", res);
   reuturn 0;
}

int add(int x, int y) {
   int sum = 0;
   sum = x + y;
   return sum;
}

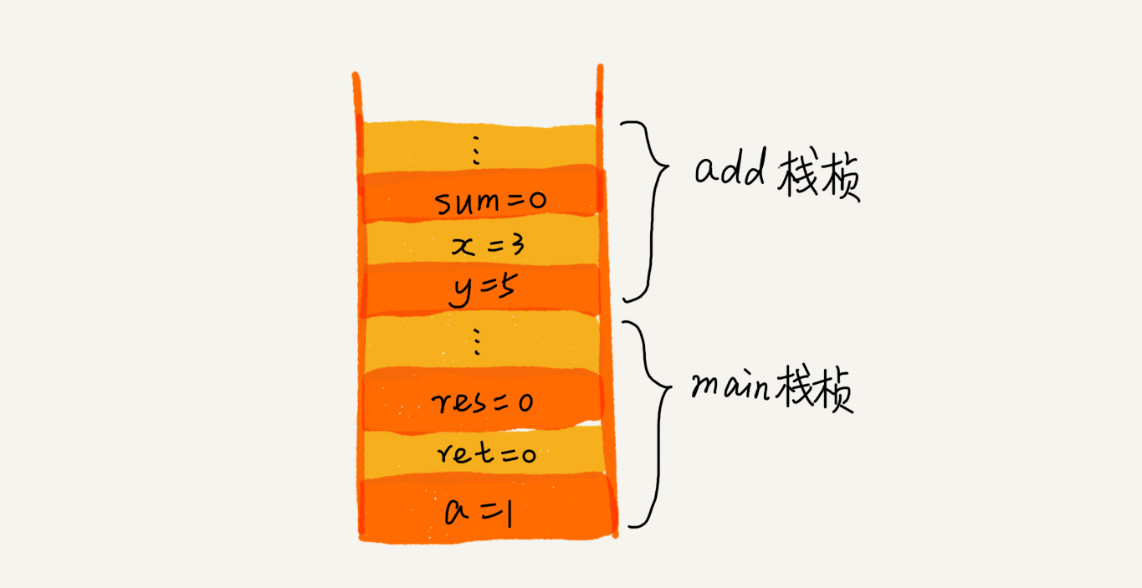
栈（stack） - 图2

表达式求值

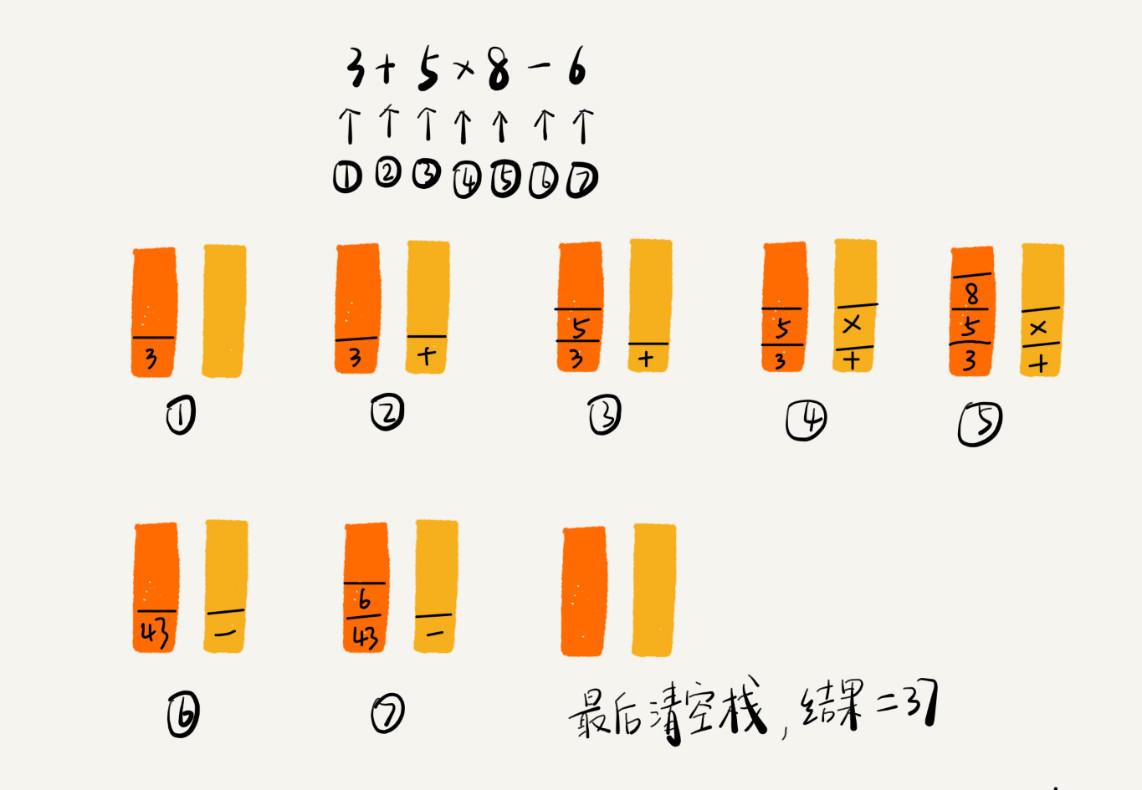
编译器就是通过两个栈来实现的。其中一个保存操作数的栈，另一个是保存运算符的栈。我们从左向右遍历表达式，当遇到数字，我们就直接压入操作数栈；当遇到运算符，就与运算符栈的栈顶元素进行比较。

如果比运算符栈顶元素的优先级高，就将当前运算符压入栈；如果比运算符栈顶元素的优先级低或者相同，从运算符栈中取栈顶运算符，从操作数栈的栈顶取 2 个操作数，然后进行计算，再把计算完的结果压入操作数栈，继续比较。

栈（stack） - 图3

括号匹配

我们用栈来保存未匹配的左括号，从左到右依次扫描字符串。当扫描到左括时，则将其压入栈中；当扫描到右括号时，从栈顶取出一个左括号。如果能够匹配，比如 “(” 跟 “)” 匹配，“[” 跟 “]” 匹配，“{” 跟 “}” 匹配，则继续扫描剩下的字符串。如果扫描的过程中，遇到不能配对的右括号，或者栈中没有数据，则说明为非法格式。

当所有的括号都扫描完成之后，如果栈为空，则说明字符串为合法格式；否则，说明有未匹配的左括号，为非法格式。

栈（stack）