LeetCode236：二叉树的最近公共祖先

题目

题目地址：

https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree/

题目描述：

给定一个二叉树，找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

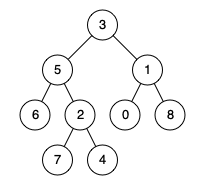
例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

示例 1:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1

输出: 3

解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

示例 2:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4

输出: 5

解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。

说明:

• 所有节点的值都是唯一的。
• p、q 为不同节点且均存在于给定的二叉树中。**（代表这棵树不为空）**
  

相关题目

思路

递归思想

根据题意，该树不为空，且 p 和 q 存在

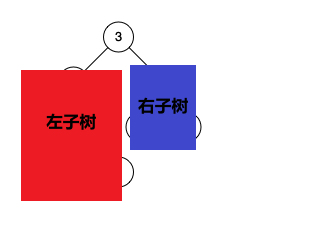
需要考虑 3 种情况

• p 和 q 分别在 root 节点的左右子树下，那么结果最近公共祖先就是 root
• p 和 q 都在左子树，那么只需要递归左子树即可
  • 如果 p 或者 q 有一个是 root，那么该 root 就是最近公共祖先
• p 和 q 都在右子树，那么只需要递归右子树即可
  • 如果 p 或者 q 有一个是 root，那么该 root 就是最近公共祖先

代码

测试用例

• 边界条件

程序

递归

时间复杂度：O(N)，其中 N 为树的节点总数
空间复杂度：O(N)，其中 N 为树的节点总数

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        # 如果 root 不存在，或者 『p 或 q 有一个是 root』    
        if not root or root == p or root == q:  
            return root
        left = self.lowestCommonAncestor(root.left, p, q) # 递归左子树
        right = self.lowestCommonAncestor(root.right, p, q) # 递归右子树
        if not left and not right:  # 如果左右子树为空，那么返回空
            return 
        if not left:  # 如果左子树为空，那么返回右子树
            return right
        if not right:  # 如果右子树为空，那么返回左子树
            return left 
        if left and right: # 如果 p 和 q 在 root 的两侧，那么返回 root
            return root