图卷积网络(GCN)数学基础

Convolution卷积

Convolution 的数学定义是

一般称 g 为作用在 f 上的 filter 或 kernel

一维的卷积示意图如下

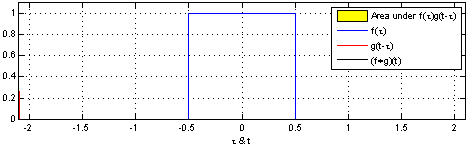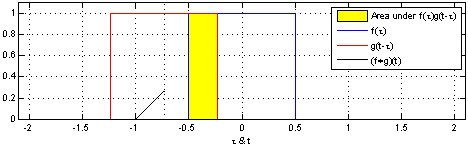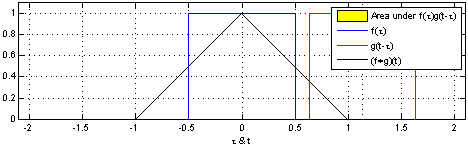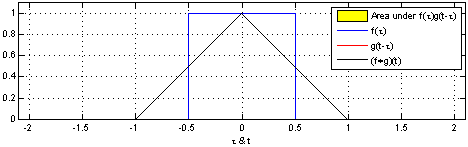
大家常见的 CNN 二维卷积示意图如下

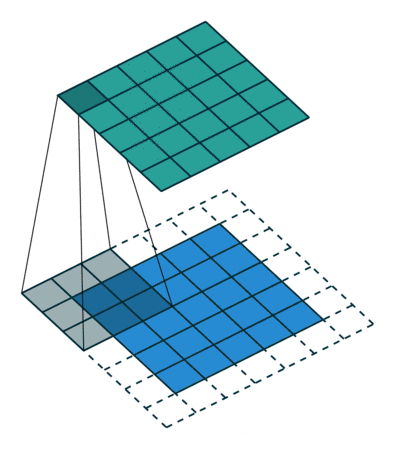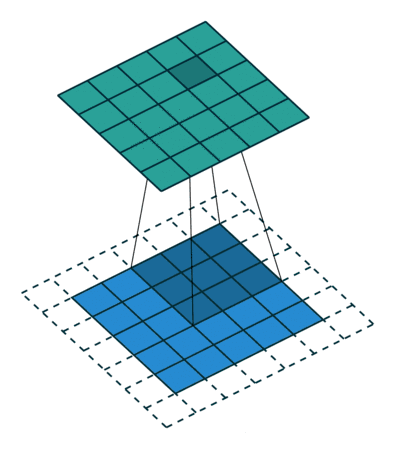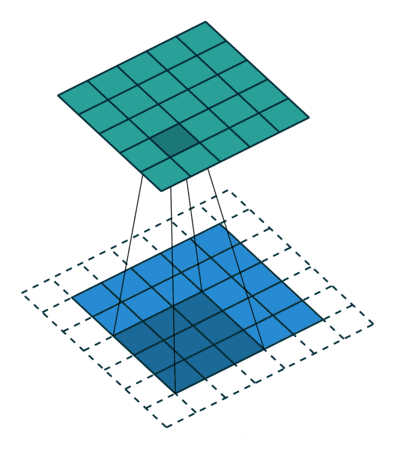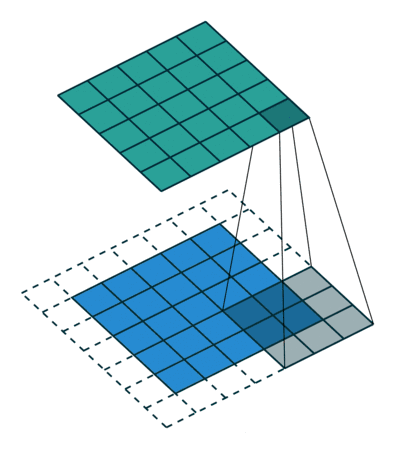
在图像里面卷积的概念很直接，因为像素点的排列顺序有明确的上下左右的位置关系。

那在抽象的 graph 里面卷积该怎么做呢

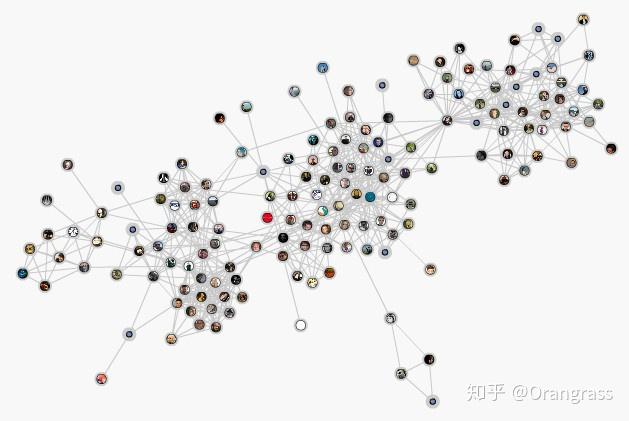
比如这个社交网络抽象出来的 graph 里面，有的社交 vip 会关联上万的节点，这些节点没有空间上的位置关系，也就没办法通过上面给出的传统卷积公式进行计算。

Fourier 变换

傅里叶变换图像展示

为了解决 graph 上卷积计算的问题，我们给出第二个装备 —Fourier 变换。

先上结论，根据卷积定理，卷积公式还可以写成

这样我们只需要定义 graph 上的 fourier 变换，就可以定义出 graph 上的 convolution 变换。

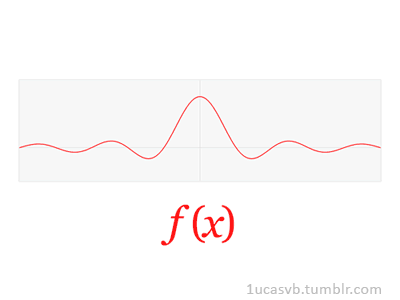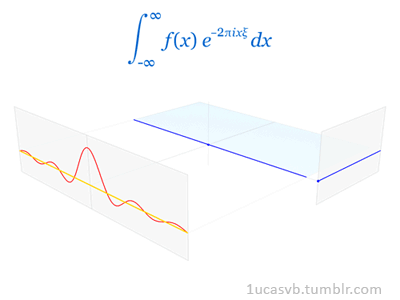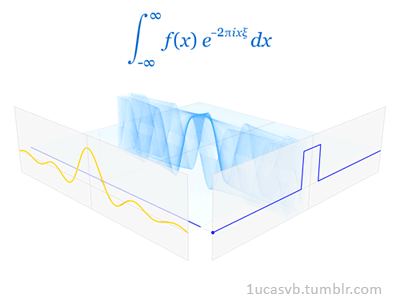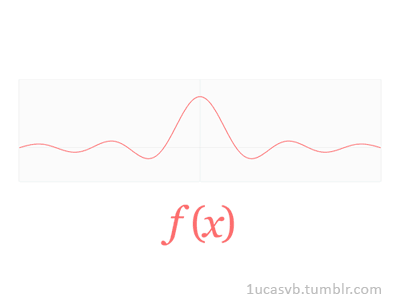
好的，先来看下 Fourier 变换的定义

Inverse Fourier 变换则是

根据 Fourier 变换及其逆变换的定义，下面我们来证明一下卷积定理

我们定义
是
和
的卷积，那么

带入
;

最后对等式的两边同时作用
，得到

Laplacian 算子

一阶导数定义为

laplacian 算子简单的来说就是二阶导数

那在 graph 上，我们可以定义一阶导数为

其中 y 是 x 的邻居节点

那么对应的 Laplacian 算子可以定义为

定义
是
的度数矩阵 (degree matrix)

定义
为
邻接矩阵 (adjacency matrix)

那么图上的 Laplacian 算子可以写成

标准化之后得到

定义 Laplacian 算子的目的是为了找到 Fourier 变换的基

比如传统 Fourier 变换的基
就是 Laplacian 算法的一组特征向量

,
是一个常数

那么图上的 Fourier 基就是
矩阵的 n 个特征向量
，
可以分解为

其中
是特征值组成的对角矩阵

那么 Graph Fourier 变换可以定义为

其中
可以看做是作用在第
个点上的 signal，用向量
来表示

是
的的对偶向量，
是矩阵
的第
行，
是矩阵
的第
行。

那么我们可以用矩阵形式来表示 Graph Fourier 变换

类似的 Inverse Graph Fourier 变换定义为

它的矩阵形式表达为

推导 Graph Convolution

下面就开始推导 GCN 的公式。

还记得我们之前提到的先上卷积定理吗

那么图的卷积公式可以表示为

作为图卷积的 filter 函数
，我们希望具有很好的局部性。就像 CNN 模型里的 filter 一样，只影响到一个像素附近的像素。那么我们可以把
定义成一个 laplacian 矩阵的函数

作用一次 laplacian 矩阵相当于在图上传播了一次邻居节点。进一步我们可以把
看做是
一个 laplacian 特征值的函数，参数为

改写上面的图卷积公式，我们就可以得到论文 SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS

的公式 (3)

可以看到这个卷积计算的复杂度是非常高的，涉及到求 laplacian 矩阵的特征向量，和大量的矩阵计算。下面我们考虑对 filter 函数做近似，目标是省去特征向量的求解

其中
是 Chebyshev 多项式。这里可以把简单
简单看成是
的多项式。

因为

所以上面 filter 函数可以写成
的函数

设定
那卷积公式可以简化为

令
，

那么再加上激活层，我们就可以得到最终的 GCN 公式

https://zhuanlan.zhihu.com/p/54505069