如果你此时已经开始急躁:“我看了八篇文章了!怎么一直在画一些不存在的事物?”
那我只能向你道歉,我们在底层和某些技术的实现上花了很多的功夫,但这是没有办法的事情,如果我们不能把地基搭好,再往后写是非常困难的。
这一章我们将正式开始为我们的无比真实的图像做努力。
我们从漫反射(磨砂)材质开始。
漫反射原理
观察一下你周围的事物,一面土墙或者你的被子又或者你的塑料手机壳,它们在敞亮的环境里是不是都很难产生明亮的高光点?你从任何角度看它们,它们的颜色都差不太多,不像是看某些金属——比如说银汤勺,强光下总有一个视角,让反射光线能正好“闪瞎”你的眼睛。
这些表面有很多微小凹凸的材质叫做漫反射材质,它们会吸收一部分光线,并且把剩余的光线朝随机方向反射出去,因为光线被反射到了不同的方向,自然不会出现某一个方向能接收到很亮的光线,也就不会有高光点存在。它们一般会吸收特定颜色的光,比如红色的砖块,它会吸收不是红色的光线,而把红色的光线按照随机方向反弹回去,所以我们看到砖块是红色的。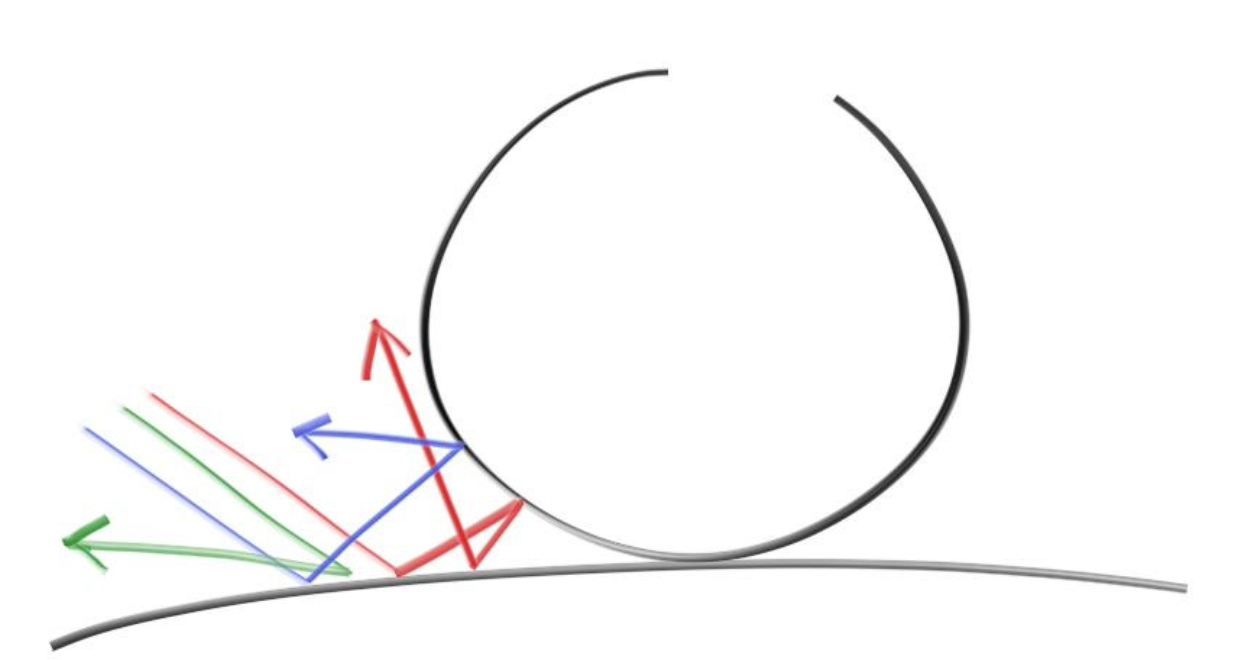
比如上图,红绿蓝三根平行光线射中漫反射材质的地面,被反射到了完全不同的三个方向。
我们把问题具象化,在代码层面我们应该如何做漫反射呢?
编程思路
因为我们现在暂时还没有光源,我们不妨假设“蓝天”就是光源(我猜你一直以为蓝天只是咱们没用的背景,但现在我要告诉你,不是的!),光的能量都是从蓝天上来的。
我们再假设任何物体对各种颜色光线的吸收率都是一样的,是1:1。光线碰撞到物体后,都会吸收掉每种光的一半的能量,然后反射一半。
又因为我们是逆光路取色,有以下n种情况:
- 我们从相机射出一根光线,这根光线没有碰到任何物体,即它射中了“蓝天”,那我们把逆光路顺过来看看这意味着什么——我们直接望到了蓝天,蓝天发出的光没有经过任何弹射直接进入了我们的眼睛。
- 我们从相机射出一根光线,这根光线碰到了一颗球,然后经过随机弹射之后,再也没有射中任何物体,朝无穷远处射出,即,它经过一次弹射之后射中了蓝天。我们把逆光路顺过来看看这意味着什么——光线从蓝天射出打到了物体上并且弹到我们的眼睛里。因为这个物体的能量吸收和反射的比率是1:1,那即表示,这根光线经过这一次弹射,只有一半的能量了。
- 我们从相机射出一根光线,这根光线碰到了一颗球,然后经过随机弹射之后,它又碰到了一颗球,我们把逆光路顺过来看——光线从蓝天射出打到了一颗球上,反射到了另外一颗球上,再反射到我们的眼睛里,没错,这根光线只剩四分之一的能量了。
……
n. 你应该能类推了,我们的光线在空间中弹射了n-1次,它的能量只剩了。
我们从相机中射出一根光线之后,只要碰撞到物体,就从这个碰撞点朝随机方向发射一根光线,然后把这根光线取到的颜色乘以0.5并返回。
我们的取色函数叫ray_color(const ray& r, const hittable& world),我们这个函数的返回值应该写什么呢?应该是return 0.5 * ray_color(newRay,world),没错吧。你应该马上明白过来了,这是一个递归,函数会疯狂的调用自己,直到某根随机反射光线射中了“蓝天”,再一层一层地返回。
我们的代码基本思路都讲完了,现在还剩一个问题,咱们一直在说光线朝随机方向反射,我们要如何制作随机反射光线呢?
单位球体积内随机选点模型
看本小节标题你可能会觉得,创建一个随机向量而已,还搞个什么模型出来,有必要么?我只能告诉你,这里面的学问大着呢!虽然不同的生成随机向量的方法都能得到看起来正确的漫反射材质,但是因为随机值的分布不同,导致结果有明显的差异,并且有优劣之分。我先给你介绍一种最容易实现的随机模型,这种模型被证明是不正确的,我们会在随后给出业界公认的正确的漫反射模型。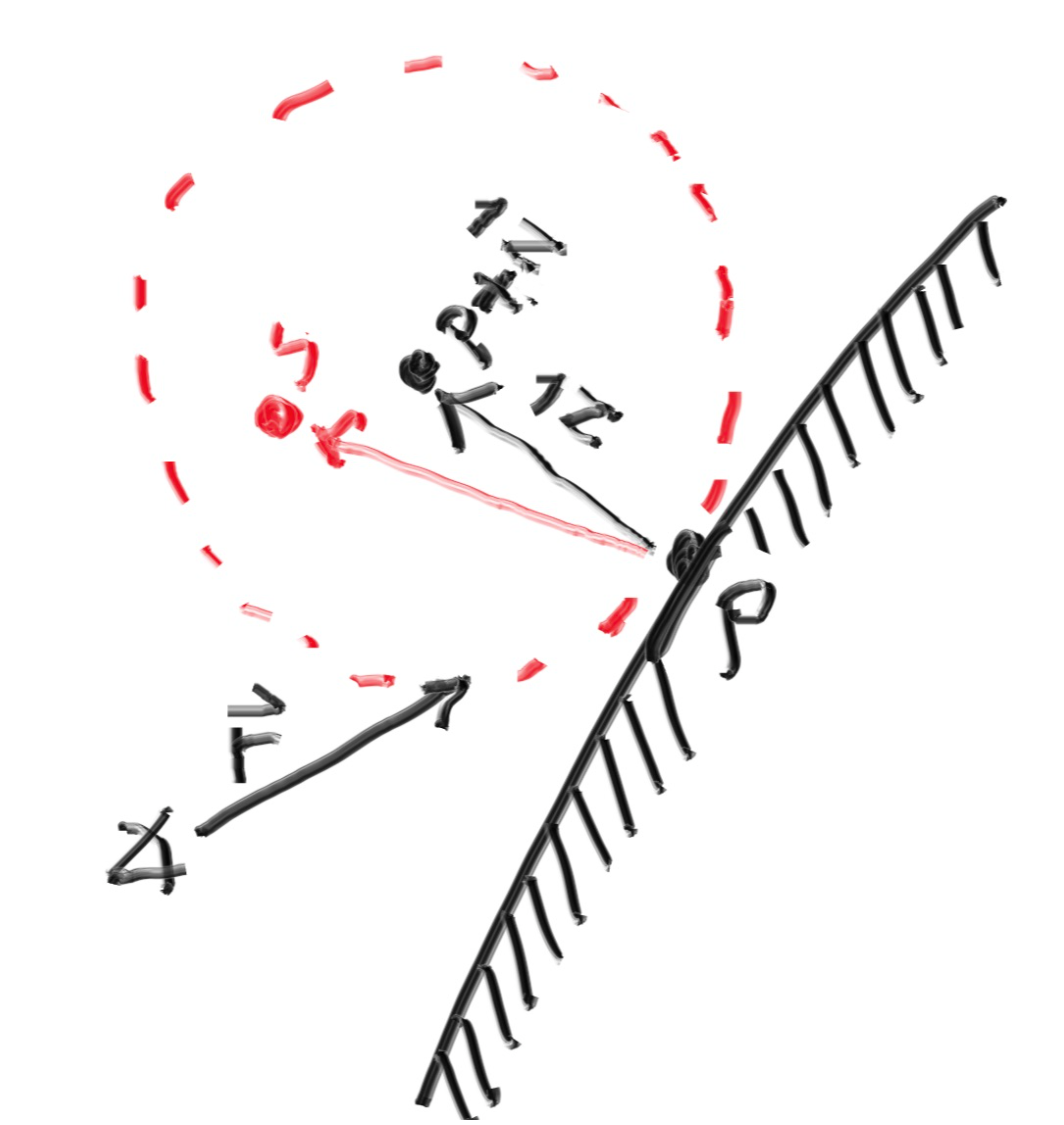
看图,碰撞点是P,法线为N(单位化),我们在以(P+N)这个点为球心的单位球内随机寻找一点S,然后以S减去P为光线的反射方向向量就是最终我们需要的向量。这个S点我们怎么得到呢?是P点坐标+N向量+一个由球心指向球内随机点的向量三部分组成。
r向量是相机观察方向,因为我们的漫反射和视角方向无关,我们不用去管它。
在上一章中我们给出了标量的随机数函数random_double(),下面先用这个函数实现一个简单的随机向量函数,在vec3.h文件中敲下如下代码:
class vec3 {public:...inline static vec3 random() {return vec3(random_double(), random_double(), random_double());}inline static vec3 random(double min, double max) {return vec3(random_double(min,max), random_double(min,max), random_double(min,max));}
我们的函数都是static的,就表示它属于整个类而不属于某个特定的对象,我们可以使用上面的函数直接调用vec3类构造生成一个三个分量都在[0,1)或者[min,max)内随机的随机vec3。<br />random() 函数生成的vec3可不是在单位球内的,它的XYZ轴都是在[0,1)之间的,它是一个在**单位立方体**内的点或者向量,我们得做一个简单的处理,让它的随机值最终落于单位球内。<br />我们再在vec3.h文件中vec3的类外写一个**全局**函数,它只有四句代码。
vec3 random_in_unit_sphere() {// 死循环?仔细看看不是啦。它有很大概率都能从return语句中脱离循环。while (true) {// 先来个中心在原点,边长为2的立方体内的点。auto p = vec3::random(-1,1);// 如果发现这个vec3的长度(它离原点的距离)大于1,即表示它是落于立方体内且落于球外的。// 我们直接让他暴力再随机一次。if (p.length_squared() >= 1) continue;// 返回一个位于单位球内的点。return p;}}
我们用一个很暴力的方法,直接让他疯狂的循环,只要点不落于单位球内,我们就让他一直随机到单位球内为止。<br />如果我告诉你,我们的标量随机函数random_double生成的随机数非常均匀,那你认为我们上述方法中随机到的点是在单位体积球内均匀分布的吗?<br />是的。<br />首先如果没有单位球的限制,咱们要的就是单位立方体内部的点,它们必然是均匀的,因为咱们三个标量都足够均匀。<br />现在加上单位球的限制,我们进行n次独立实验(n足够大),我们把这n次实验的结果按照随机几次才得出结果再分成m堆。<br />首先是最大的那一堆,这一堆中的点都是只随机一次就落在了单位球内的,有个点在这个堆里(球的体积比上立方体体积)。这些点必然均匀。因为咱们的随机点肯定均匀分布于立方体,也必然均匀分布于立方体中的球内。<br />接下来看看第二大的那个堆,这个堆里的点都是第一次随机到了球外,第二次随机到了球内的,这部分的点有个。如果只针对这一批点来说,肯定也是均匀分布于球内(因为我们采用的算法并没有改变)。<br />以此类推我们就能得出整体必然均匀的结论。<br />既然整体都是均匀的,为什么我会说它是不正确的呢?容我卖个关子,咱们先把图片渲染出来。我会在下一章介绍正确模型之后再讨论这个问题。
更新着色代码
经过我们在编程思路阶段分析的内容,我们可以修改ray_color函数如下:
color ray_color(const ray& r, const hittable& world) {hit_record rec;if (world.hit(r, 0, infinity, rec)) {//提到过的三部分组成的S点坐标。point3 target = rec.p + rec.normal + random_in_unit_sphere();//提到过的步骤,创造新的光线并开启下一轮递归。return 0.5 * ray_color(ray(rec.p, target - rec.p), world);}vec3 unit_direction = unit_vector(r.direction());auto t = 0.5*(unit_direction.y() + 1.0);return (1.0-t)*color(1.0, 1.0, 1.0) + t*color(0.5, 0.7, 1.0);}
完全按照思路进行的编程。
如果你这个时候已经开始对我感到不屑:“呔!你在main函数所在文件中怎么能如此胡作非为呢?”
我会很欣慰你听进去了我之前一遍又一遍的给你洗脑代码规范问题。没错,这么做意味着咱们修改了本项目中最重要的光线取色函数,让它把所有的物体都当作漫反射物体来处理。我们这样做扼杀了我们以后制作其他种类材质的可能性。而且在这样的代码里,我们无法指定球A是漫反射体,而球B是其他材质。现在所有的一切都是漫反射体了,就好像我们要做的不是“光追器”,而是“漫反射体模拟器”了。
这显然是不合理的。
但是这里,为了行文的流畅性,我们还是采取先污染表层代码,在治理污染,把内容抽象到深层的过程来做。这个思路应该也是我们平时写代码的思路,在实现某一个特定功能的时候,除非我们已经画出了完善的类图并有良好的框架搭建经验,不然按照这个思路来写代码是最正确的选择:对于不自信的内容,先写到表层实现需求,再抽象到底层维护框架。
至此我们除了细节问题之外,完成了漫反射的主要代码。你会发现虽然我们花了很长的篇幅来介绍漫反射,但是它真的写进代码里还是非常简单的——因为我们有递归。
修复被炸毁的栈
尝试运行程序的代码试试看,发现根本就运行不了。
如上图所示,命令行直接被强制终止了,我们的程序根本就没能运行完!这是为什么呢?联想到我们添加的代码是递归代码,立马大致猜到问题的所在——递归无法终止吗?
咦?我们明明已经设置了递归的终止条件——射中“蓝天”。为什么它没能正确终止呢?
因为系统栈是有大小限制的。
假设有一根光线射中了两颗球的接触的地方,这个地方极其的狭窄,光线在两颗球之间反复弹跳了上千次都没能弹射出去,这对我们的程序将是可怕的灾难。我们的函数不断递归调用自己,把一遍又一遍的必要信息压入栈,压了几千次几万次,都没能等来一个信息出栈的机会。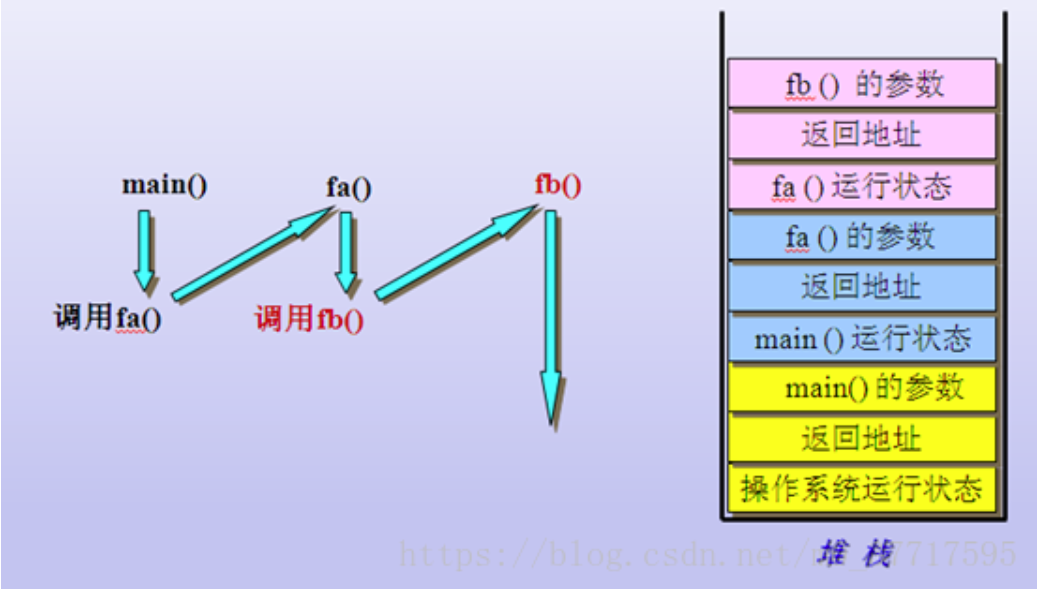
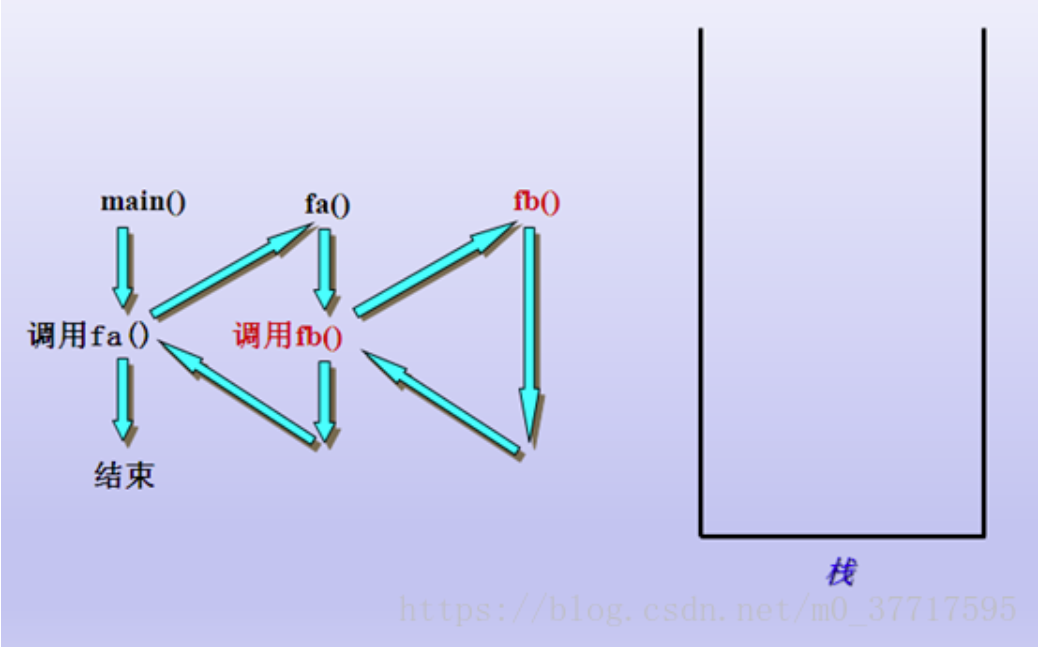
上图是经典的函数调用压栈模型。我们的程序在函数疯狂自我调用中炸毁了系统栈。
我们需要限制光线的弹射次数,在光线弹射次数达到我们规定的次数的时候,消灭它,让他直接返回黑色——这表示能量消耗殆尽了。
color ray_color(const ray& r, const hittable& world, int depth) {hit_record rec;// 如果次数消耗殆尽,直接终止递归,我们的系统栈可耗不起了!if (depth <= 0)return color(0,0,0);if (world.hit(r, 0, infinity, rec)) {point3 target = rec.p + rec.normal + random_in_unit_sphere();//每一轮新的递归,我们把光线可弹射次数减一。return 0.5 * ray_color(ray(rec.p, target - rec.p), world, depth-1);}vec3 unit_direction = unit_vector(r.direction());auto t = 0.5*(unit_direction.y() + 1.0);return (1.0-t)*color(1.0, 1.0, 1.0) + t*color(0.5, 0.7, 1.0);}int main() {...const int samples_per_pixel = 100;//给定光线最大弹射次数。const int max_depth = 50;...for (...) {...//更改ray_color调用代码。pixel_color += ray_color(r, world, max_depth);}}
修改完毕后,程序已经可以运行了,你会得到下面的图案:<br /><br />它看上去非常的暗,但你放大看看,我们已经可以看到漫反射材质的细节了。但是...它为什么会这么暗呢?<br />我们只看上方小球的球顶,常识告诉我们,光线打到这里,很大概率能反弹到蓝天上,也就是说,它的颜色应该趋向于蓝天的颜色衰减了一半之后的某种蓝色。而我们的图像并非如此。<br />另一种方法也可以佐证我们的看法,用文本模式打开ppm文件,你会看到上边右图中的RGB值,它们都是很靠近黑色的值,我们的程序似乎就没生成过只弹射一次就碰到蓝天的光线,这是为什么呢?
课后实践
- 思考一下本章中提到的几个问题:
- 我们的单位球体积内随机选点模型更容易生成和法线夹角较小的反射方向还是更容易生成和法线成大角度的反射方向?
- 你觉得是什么原因导致我们的首张漫反射图像显得如此的暗?
我们会在下一章中解答这些问题,给出其他的随机模型,并生成一张完美的漫反射图像。
- 如果光线是从球内打到球的内壁上,我们代码能正确的运转吗?
参考文献
https://raytracing.github.io/books/RayTracingInOneWeekend.html
参考自《RayTracingInOneWeekend》第8.1节到8.3节。
https://blog.csdn.net/m0_37717595/article/details/80368411
C/C++函数调用的压栈模型。

