在上一章中,我使用了递归衰减能量以及单位球体积内随机选点模型,实现了一个看起来偏暗的漫反射材质,这一章里,我会修复图像过暗问题,以及介绍两种其他的随机选点模型,并讨论几种模型的区别。
拒绝“内耗”,重回自我
我们先来解决导致我们画面太暗的罪魁祸首——浮点精度问题。
我们生成反射光线的起点是碰撞点,但是因为浮点数并不能精确的等于某个数,比如double d = 0;,实际的项目运行过程中,d不会精确等于0,而是会等于诸如-0.00000083之类的逼近0的小数。
咱们的球面方程非常严谨,稍微偏差了一分一毫都会出问题。浮点数精度问题会导致一部分光线的起点在球的内部,这样发射光线,光线会和球的内壁碰撞,然后在球内反复弹射,耗尽自己的一生。
我们可以通过微移光线起点的方式来解决,但是这样会把问题复杂化。别忘了我们在写hit函数的时候,留有限制t的参数t_min和t_max。我们完全可以使用t_min的限制,让光线自动忽略那些和发射点很近的物体。
如下:
if (world.hit(r, 0.001, infinity, rec)) {...}
再运行代码,我们发现这次生成图片的时间快了很多,以及可以看到清晰的图像了:
认清“理想”和“现实”的差距
我们得到了两个深灰蓝色的球,我们的图形从纯粹的物理学意义上来说没有什么毛病了,但是从某些角度来说,依然存在问题。
人的眼睛并不是精准的机器,它对亮度的感知和实际能量的功率是不成线性函数关系的,而是幂函数关系,这个函数的指数通常为2.2,称为Gamma值。
也就是说,如果光线真的是每次碰撞到物体都衰减一半的能量,那对于百分之50功率的灰色,人眼实际感受到的亮度为,是一种偏向于白色的淡灰色。
而人眼中的中灰色,实际上是功率只有。
我们需要为了适应人眼去纠正光线的能量,让它符合人眼生物学中的颜色,这叫做伽马矫正。
为了方便,我们并不需要那么精准,我们使用”Gamma 2”矫正,即直接对最后的颜色值开方,在write_color函数中,有:
void write_color(std::ostream &out, color pixel_color, int samples_per_pixel) {auto r = pixel_color.x();auto g = pixel_color.y();auto b = pixel_color.z();//Gamma矫正(Gamma = 2.0)。auto scale = 1.0 / samples_per_pixel;r = sqrt(scale * r);g = sqrt(scale * g);b = sqrt(scale * b);out << static_cast<int>(256 * clamp(r, 0.0, 0.999)) << ' '<< static_cast<int>(256 * clamp(g, 0.0, 0.999)) << ' '<< static_cast<int>(256 * clamp(b, 0.0, 0.999)) << '\n';}
这会让我们图像看起来更亮,你现在看到的图像中的球,才是真实世界中,光线能量对半衰减之后的漫反射材质。<br /><br />如果你觉得还是咱们之前的图好看,就去修改光线的衰减比例,让他每次衰减的多一点。无论如何,上面的图像才是更正确的。
相信并拥抱“真理”
现在还差最后一个问题,我们的随机点选取方式是错误的。虽然在单位球体积内随机选点,看似是在空间中均匀的,但是它更容易产生靠近法线的反射方向。我们就不给出具体的概率分布函数,通过另外更简单直接的方式来理解单位球体积内随机选点模型更“喜欢”生成什么样的反射方向。
我们就以45°角为分界线,看看什么情况下该模型会生成和法线夹角小于45°的反射方向。因为选点在空间中是均匀的,我们可以简单的理解为,满足条件所在的点的区域的体积越大,概率越大,那什么情况下我们会得到小于45°的反射方向呢?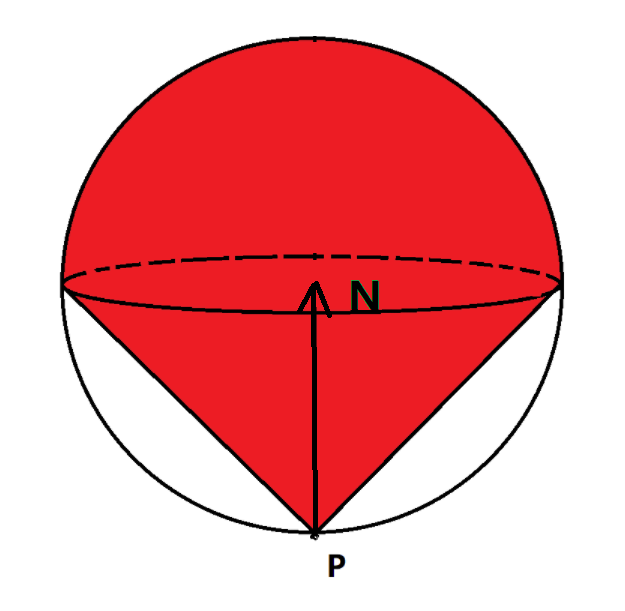
如上图所示,P点射往图中红色区域的点所构成的反射方向和法线的夹角会小于45度。可以发现体积选点模型更倾向于选择靠近法线方向的点。它对于靠近法线的反射方向太偏心了!
而在现实生活中,纯粹的漫反射材质产生的随机反射光线不会像上图那样分布,我们下面给出能生成最贴合现实世界物理规律的漫反射材质的反射方向的模型。
很简单,我们只需要把体积的随机改成面积的随机即可,我们在单位球的表面随机选点。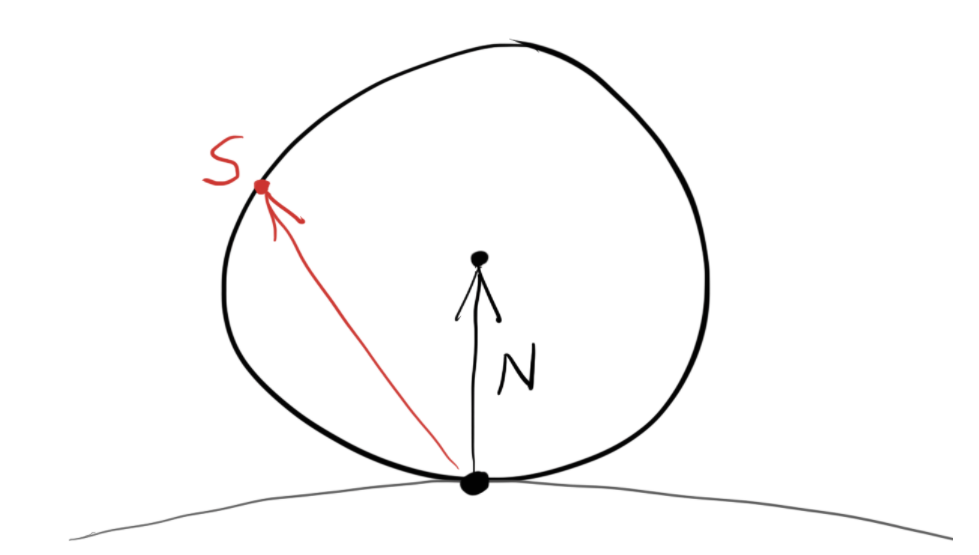
看代码,在vec3.h文件中加入如下全局函数:
inline vec3 random_in_unit_sphere() {...}vec3 random_unit_vector() {return unit_vector(random_in_unit_sphere());}
再修改ray_color函数中的代码:
color ray_color(const ray& r, const hittable& world, int depth) {...if (world.hit(r, 0.001, infinity, rec)) {// 这次改为在球面上取点。point3 target = rec.p + rec.normal + random_unit_vector();...}...}
你会得到这张图:<br /><br />我们来看看我们介绍的单位球表面随机选点模型——又称真实兰伯特模型(true Lambertian)的概率分布。我们依然以45°角为分界,看看和法线夹角小于45°的点是哪一部分。<br />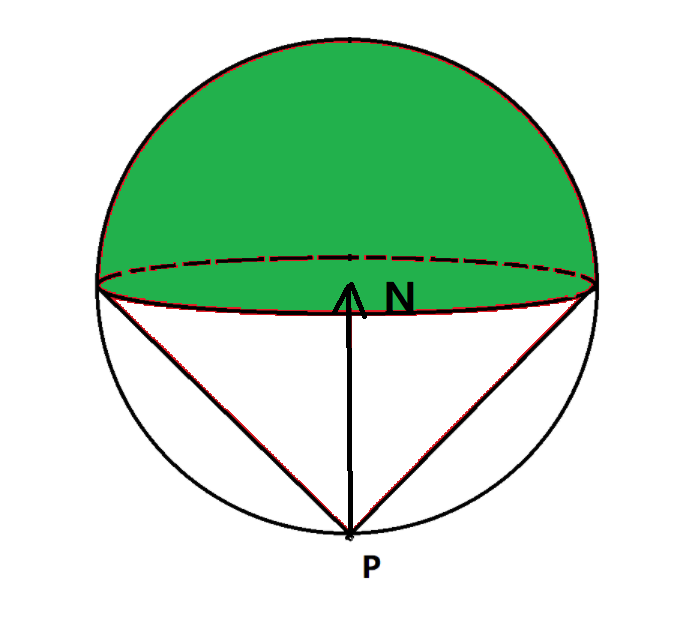<br />如图所示,绿色部分既是和法线夹角小于45°的反射方向所对应的点的区域,它正好是整个球面积的二分之一。说明对于这个模型,随机选点所产生的反射方向更为公平。<br />该模型也是现在业界公认的正确漫反射模型,或许在你看来,这个模型和体积选点模型所生成的图像看上去虽有差别,但是也说不清楚哪个更为正确——这是因为我们在日常生活中很难看到完全漫反射的物体,你对这类事物的视觉直觉很差。但你只要记住,后者才更符合现实中的漫反射,是更正确的。
致敬“前人的智慧”
在本章的最后,我们来看一下一种更容易想到的模型——半球表面选点模型,很多早期的光线追踪论文使用的是这样一种模型。
在以碰撞点P为球心的单位半球内找点,取点半球和表面法线在面的同侧。继续添加一个vec3.h的全局函数。
vec3 random_in_hemisphere(const vec3& normal) {vec3 in_unit_sphere = random_in_unit_sphere();// 如果该向量和法线夹角为锐角,即在面的同侧,接受它,否则取反。if (dot(in_unit_sphere, normal) > 0.0)return in_unit_sphere;elsereturn -in_unit_sphere;}
同样更改ray_color中的调用方式。
point3 target = rec.p + random_in_hemisphere(rec.normal);
你会得到下图:
随后我们的项目会越来越大,你可以在之后的项目里,尝试在三种漫反射模型中切换,通过了解不同漫反射方法对场景的影响,你可能会学到更多东西。
下一章开始,我们会把漫反射的代码从main函数中移走,并且为了实现物体和其光线作用方式分离,我们需要抽象出材质类,在这之后我们还会迎来我们的第二种材质——金属。
课后实践
- 生成三种随机模型下的图片,进行对比,观察不同。为什么兰伯特模型得到的阴影比体积球模型要少?为什么半球模型得到的阴影要比前两者更小?
- 记兰伯特模型中,反射光线和法线的夹角为ϕ,请探究通过模型取到和法线角度小于ϕ的反射方向概率f(ϕ)和ϕ的关系。
- 尝试只修改main函数所在文件代码,绘制《太极》。《太极》如下图所示,你生成的图片可以和下图有些许不同(下图使用体积球随机选点模型),但必须得有 :
1) 天空中明确的分界线。
2) 一些以分界线为对称轴的小球。
- 尝试只修改main函数所在文件代码,绘制《炽日》。《炽日》如下图所示,你生成的图片可以和下图有些许不同(下图使用体积球随机选点模型),但必须得有 :
1) 天空中的“炽日”。
2) “炽日”打在物体上的“光辉”。
- 尝试修改任意代码,绘制《灯》。《灯》如下图所示,你生成的图片可以和下图有些许不同(下图使用兰伯特模型),但必须得有:
1) 至少一个用于照明的灯球。
2) 一些各色的球。
参考文献
https://raytracing.github.io/books/RayTracingInOneWeekend.html
参考自《RayTracingInOneWeekend》第8.3节到8.6节。

