在制作完三种材质之后，我们终于要开始摆弄相机了。相机调试起来是非常痛苦的，我们尽量把问题切开切碎来看。我们现在的相机是一个什么样的相机？
我们的相机： ①放在原点处。②朝负z方向看。③虚拟视口放置于z=-1处。④虚拟视口高度始终为2。⑤长宽比始终为16：9。
全都是常量！它身上的枷锁还真不少。
接下来我们会逐步解放相机，让他变得自♂由。首先，我们先让虚拟视口不再被约束。让虚拟视口大小自由可定义，这可以有效解决我们图片边缘的球被明显拉长的问题。

为什么球会被拉长？

在《球》那一章的问题与思考里的第二小题中提到过这个问题，我不知道你是否想明白，在这里我会用浅显易懂的语言回答这个问题，如果你已经想明白了，可以不用听我废话直接去看下一个小节。
我们先来解释为什么在图片两侧的球会被水平拉长变形，竖直方向的变形可以用同样的理论解释。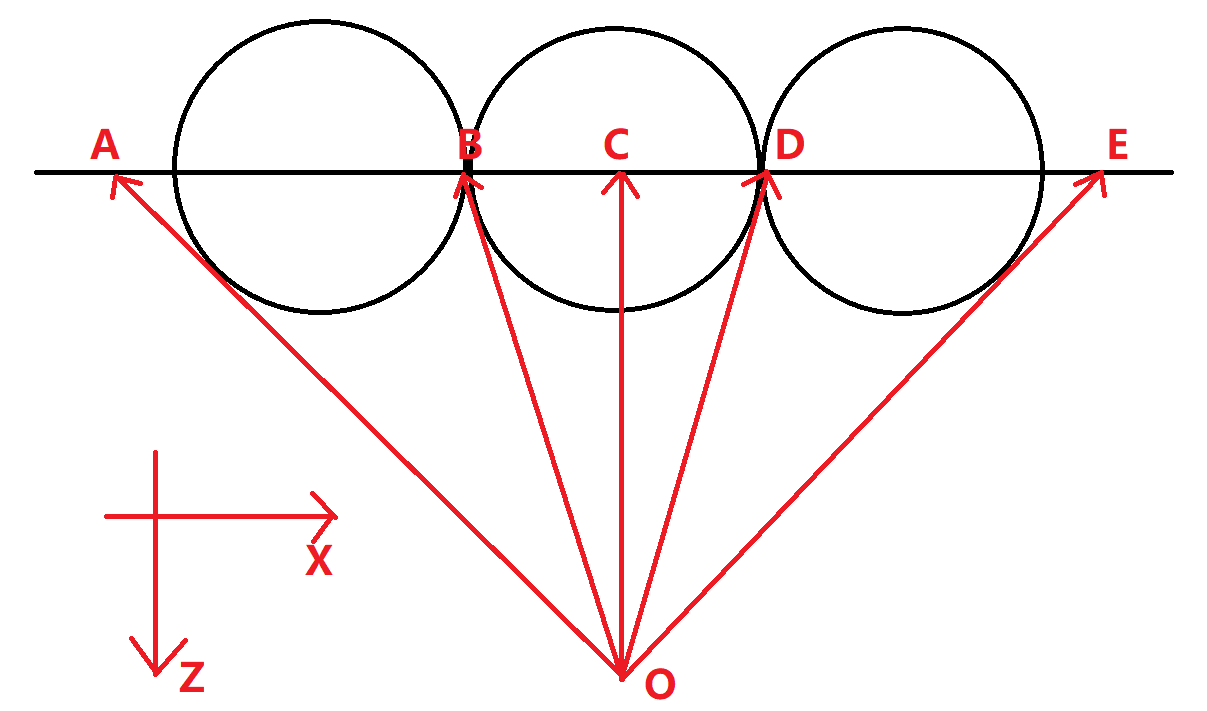
image.png
上图是y = 0的情况下，场景的 XoZ面截面。O为相机位置，也是发射光线的原点，横线为Z = -1 位置上的虚拟视口，在空间中有三个大小一样的球，三个球的球心都在y = 0平面上，中间的那颗球处在虚拟视口的正中心，即它的位置是(0,0,-1)。我们现在开始往虚拟视口上发射光线，来看看每颗球x轴上的宽度是多大。
可以清楚的看到，A点虽然在虚拟视口上来看，和球还是有点距离，但是我们往A点发射光线来确定这一点的颜色的时候，发现它正好处于球的边界上，即在我们最终渲染的2D图片上，AB才是这颗球与x轴平行的直径，它显然比2D图片上处于中间的球的直径BD要长的多。
那我们如何对抗图片边缘变形问题呢？有两个解决方法：让虚拟视口变得非常小，或者让虚拟视口离相机位置足够远。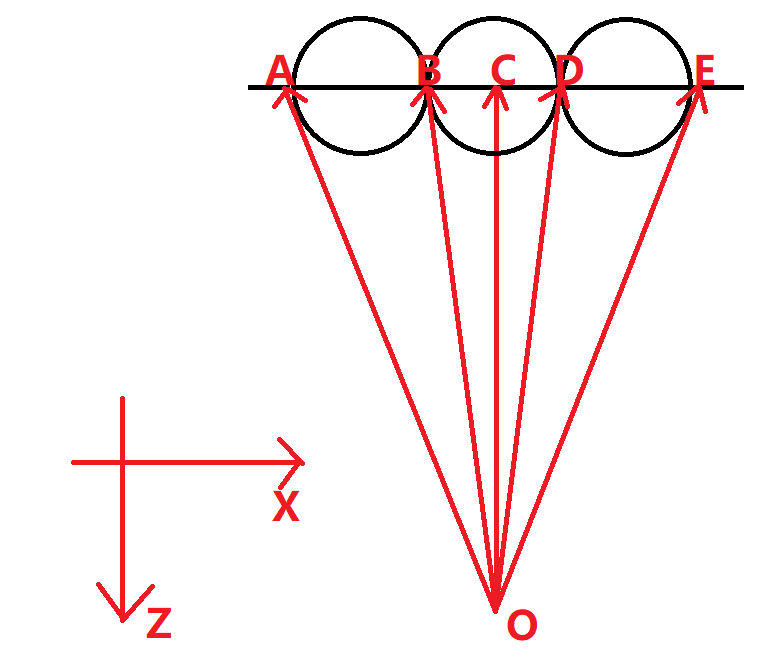
image.png
如图所示，我们把虚拟视口缩小，这样图中的三个球在最终显示的图片上来看就不会有非常明显的长度不一的问题了。因为视口变小，视口中的像素数量不变，所以每个像素在三维空间中的大小也变小了，所以图片的最终质量并不会有任何改变。

可调节视野

虚拟视口的长宽比不应该被限制，同时虚拟视口的高度也不应该恒定为2，假设有一个物体在我们的面前但是高度很高，比如它在(0,10,-1)的位置，它不会被我们的相机捕捉到，我们得赋予它自由度，让他想看多高看多高。
对于方形的照片，在真实的摄影技术中，有一个数据叫视场(field of view)，简写为fov，我们一般使用的是竖直fov，它表示相机处到视野最高处和视野最低处连线的夹角，如果是水平fov的话就是相机处和视野中最左最右处连线的夹角。如果知道长宽比的话，竖直和水平的fov就可以进行简单换算。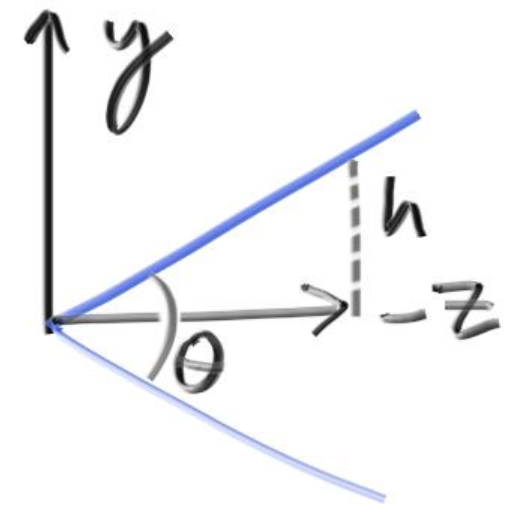
image.png
如图所示，θ就是fov，我们就使用指定fov的方式来让视口高度变得可自定义。
还有一点纯属个人设计风格：我们传入角度值，再由类内转为弧度制进行后续计算。
修改camera.h中的camera类代码如下所示：

  1. class camera {
  2.     public:
  3.         camera(double vfov /*竖直fov（vertical field of view）*/ 
  4.                ,double aspect_ratio /*长宽比，把它暴露出去使之可自定义*/ ) {
  6.             //角度转弧度制，我们好久之前写的工具函数。
  7.             auto theta = degrees_to_radians(vfov);
  9.             //虚拟视口还是放在z = -1的地方。
  10.             auto focal_length = 1.0;
  12.             //通过换算得到上图中的h。
  13.             auto h = focal_length * tan(theta/2);
  15.             //这样虚拟视口就一步一步由fov换算得来了。
  16.             auto viewport_height = 2.0 * h;
  18.             auto viewport_width = aspect_ratio * viewport_height;
  19.             origin = point3(0, 0, 0);
  20.             horizontal = vec3(viewport_width, 0.0, 0.0);
  21.             vertical = vec3(0.0, viewport_height, 0.0);
  22.             lower_left_corner = origin - horizontal/2 - vertical/2 - vec3(0, 0, focal_length);
  23.         }
  25.         ray get_ray(double u, double v) const {
  26.             return ray(origin, lower_left_corner + u*horizontal + v*vertical - origin);
  27.         }
  29.     private:
  30.         point3 origin;
  31.         point3 lower_left_corner;
  32.         vec3 horizontal;
  33.         vec3 vertical;
  34. };
  1. 我们来测试一下我们的修改，在main函数中更换场景，并用新的构造函数创建相机：
  1. int main() {
  2.     ...
  4.     // 指定视场大小
  5.     double vfov = 10.0;
  7.     // 更改物体信息。
  8.     hittable_list world;
  10.     auto material_up = make_shared<lambertian>(color(1, 0, 0));
  11.     auto material_bottom = make_shared<lambertian>(color(0, 0, 1));
  13.     // 我们想创造两个球心在边界上的球。
  14.     auto R = tan(degrees_to_radians(vfov) / 2);
  15.     world.add(make_shared<sphere>(point3(0, R, -1), R, material_up));
  16.     world.add(make_shared<sphere>(point3(0, -R, -1), R, material_bottom));
  18.     // 定义一个vfov是10度的相机，并且传入我们之前定义在main中长宽比。
  19.     camera cam(vfov, aspect_ratio);
  21.     // 渲染循环
  22.     std::cout << "P3\n" << image_width << " " << image_height << "\n255\n";
  23.     for (int j = image_height-1; j >= 0; --j) {
  24.     ...

你会得到两个图片边缘的球，它们没有再被明显的拉长了，因为fov = 10° 的情况下，虚拟视口的大小比原来小得多（之前我们的高度h恒定为2的情况，fov按照反向换算应该为90°）。
image.png

完全自由相机

在视野大小和长宽比可以调整之后，我们相机身上的五个枷锁中的后两个已经解开，现在还有三个固定死的桎梏。接下来只要让相机的位置和朝向可以自由选定，就可以让相机彻底解放。
先提一嘴，我们的虚拟视口大小可以通过fov自由控制之后，我们就没有必要再改变虚拟视口离相机的远近了，这不会给场景带来更多新的变化。我们缩小虚拟视口，实际上和把虚拟视口拉远得到的效果是完全一样的，我们固定死它，假设这个距离恒定为1。
进入正题。
我们需要自由指定相机的位置，也就是说我们要暴露出一个point3(vec3的别名)变量来表示位置，这很容易想到。
那我们要如何指定相机看向的方向呢？有两个策略，给一个方向向量或者给定一个点表示看向的目标点，这样就可以通过和相机位置的连线得到同样方向向量，我们选择后者。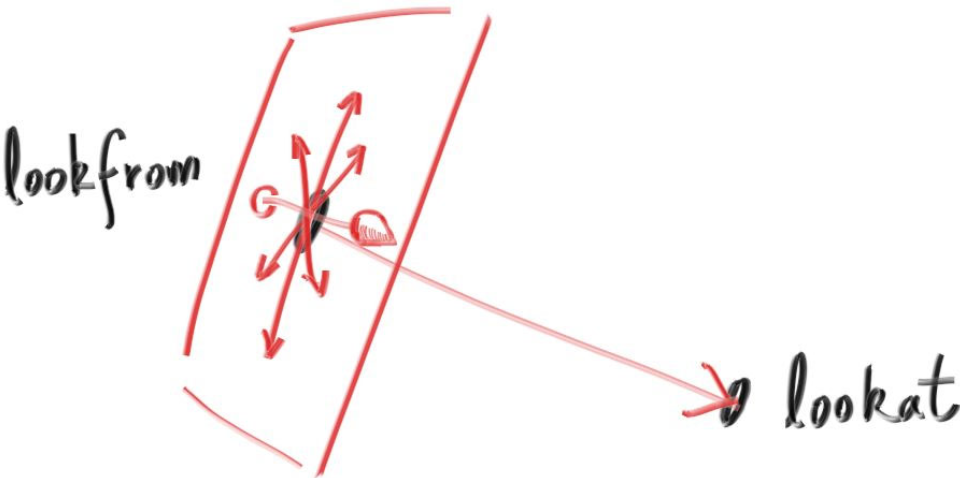
image.png
看图，相机放在lookfrom点上，看的目标点是lookat。
fov我们也已经有了，现在我们能开始构建相机了吗？不能，还有一个东西我们没法确定。想想看，你站在某个地方，望着桌子上的苹果，苹果一定会处在你视角的正中心，但是，我无法确定你有没有以你的鼻子为中心左右旋转你的头——在lookfrom所在的面和lookat-lookfrom向量垂直的向量有无数多条，我们不知道，相机的“头顶”是哪个方向。
这个问题，业界比较青睐的解决方案是确定一个vup（view up）方向，一般来说，只要你不歪头，这个vup的值都是(0,1,0)，即y轴正方向。但是搞不好就有一些特殊的要求，比如说，从墙角伸出一杆狙击枪，我们需要歪头去看瞄准镜，这时候，瞄准镜内的世界就是歪斜的，vup就会指向斜上方。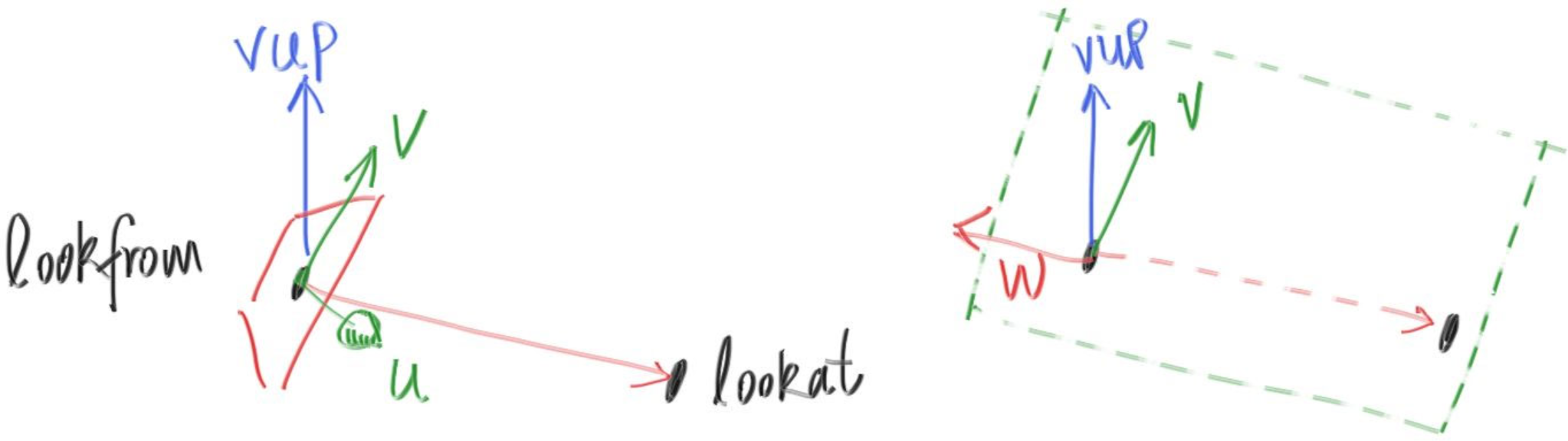
image.png
看上左图，lookfrom、lookat和vup向量唯一确定了一个相机。
左图中的uv两个坐标轴，也就是我们的老相机里面的horizontal和vertical向量。
老相机是朝-z方向看的，而新的相机是朝-w（上右图中的向量）方向看的。右图中w,v和vup三个向量在同一个面上。
我们的最终相机代码如下：

  1. class camera {
  2.     public:
  3.         camera(
  4.             // 相机位置。
  5.             point3 lookfrom,
  6.             // 相机看向的目标点。
  7.             point3 lookat,
  8.             // 相机正上方方向向量（通常为(0,1,0)）。
  9.             vec3   vup,
  10.             // 视场大小。
  11.             double vfov,
  12.             // 长宽比。
  13.             double aspect_ratio
  14.         ) {
  16.             auto theta = degrees_to_radians(vfov);
  17.             auto h = tan(theta/2);
  18.             auto viewport_height = 2.0 * h;
  19.             auto viewport_width = aspect_ratio * viewport_height;
  21.             // w向量是从lookat指向lookfrom的向量。
  22.             auto w = unit_vector(lookfrom - lookat);
  24.             // u向量与vup和w都垂直，我们可以直接叉乘得到它。
  25.             // 叉乘注意两个变量的前后顺序，注意叉乘结果向量的方向满足右手定则。
  26.             auto u = unit_vector(cross(vup, w));
  27.             // v向量与w及u向量都垂直，叉乘得到。
  28.             auto v = cross(w, u);
  30.             // 赋值原点。
  31.             origin = lookfrom;
  32.             // horizontal方向不再是(1,0,0)，而是u。
  33.             horizontal = viewport_width * u;
  34.             // vertical方向不再是(0,1,0)，而是v。
  35.             vertical = viewport_height * v;
  37.             // 虚拟视口左下角的坐标位置，原本减去vec3(0, 0, focal_length)的位置改成了w。
  38.             lower_left_corner = origin - horizontal/2 - vertical/2 - w;
  39.         }
  41.         ray get_ray(double s, double t) const {
  42.             return ray(origin, lower_left_corner + s*horizontal + t*vertical - origin);
  43.         }
  45.     private:
  46.         point3 origin;
  47.         point3 lower_left_corner;
  48.         vec3 horizontal;
  49.         vec3 vertical;
  50. };

虚拟视口离相机的距离由w决定，它是个单位向量，永远是1。前面我们讨论过，我们打算写死虚拟视口和相机之间的距离——我们不需要动他，改变fov能达到相同的效果。
在main函数中改变场景物体和相机参数，我们来测试一下这个自由的相机。

  1. hittable_list world;
  3. auto material_ground = make_shared<lambertian>(color(0.8, 0.8, 0.0));
  4. auto material_center = make_shared<lambertian>(color(0.1, 0.2, 0.5));
  5. auto material_left   = make_shared<dielectric>(1.5);
  6. auto material_right  = make_shared<metal>(color(0.8, 0.6, 0.2), 0.0);
  8. world.add(make_shared<sphere>(point3( 0.0, -100.5, -1.0), 100.0, material_ground));
  9. world.add(make_shared<sphere>(point3( 0.0,    0.0, -1.0),   0.5, material_center));
  10. //空心玻璃球不要紧贴其他物体，否则会产生黑点。
  11. world.add(make_shared<sphere>(point3(-1.001, 0.0, -1.0), 0.5, material_left));
  12. world.add(make_shared<sphere>(point3(-1.001, 0.0, -1.0), -0.45, material_left));
  13. world.add(make_shared<sphere>(point3( 1.0,    0.0, -1.0),   0.5, material_right));
  15. camera cam(point3(-2,2,1), point3(0,0,-1), vec3(0,1,0), 90, aspect_ratio);

相机原点放在(-2,2,1)上，这离场景中的这些球很远，所以我们会得到：
image.png
fov为90的情况下，虚拟视口的高度为2，球处在我们图片的正中心，但很小.
如果我们想得到近景，只需要把fov改小，比如改成20，就可以得到清晰的细节，就好像使用了望远镜一样。

  1. camera cam(point3(-2,2,1), point3(0,0,-1), vec3(0,1,0), 20, aspect_ratio);
  1. 你会得到：<br />![image.png](https://cdn.nlark.com/yuque/0/2022/png/25639626/1643953583323-2fbaf10f-719c-4d89-a1b7-2c746b02719c.png#clientId=u15a0dcb1-edea-4&crop=0&crop=0&crop=1&crop=1&from=paste&height=289&id=ue8936579&margin=%5Bobject%20Object%5D&name=image.png&originHeight=651&originWidth=1150&originalType=binary&ratio=1&rotation=0&showTitle=false&size=199868&status=done&style=none&taskId=u96310dd9-1a39-40fd-a616-fb6c290078b&title=&width=511.1111111111111)<br />`const int image_width = 400`的配置下，也可以得到漂亮的细节！<br />项目第一阶段即将完成，不知不觉这一本《Ray Tracing in One Weekend》也要被我们读完了。在本阶段的最后一篇文章中，我会实现最后一个需求——散焦模糊，再绘制一个稍微复杂一点的场景作为收尾。<br />让我们一起为曾走过的这么长的路而狂欢吧！

参考文献

https://raytracing.github.io/books/RayTracingInOneWeekend.html
参考自《RayTracingInOneWeekend》第11节。