剑指Offer 62：
圆圈中最后剩下的数字？0,1,···,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字（删除后从下一个数字开始计数）。求出这个圆圈里剩下的最后一个数字。

例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3

问题类型

这个问题是以弗拉维奥·约瑟夫命名的，他是1世纪的一名犹太历史学家。他在自己的日记中写道，他和他的40个战友被罗马军队包围在洞中。他们讨论是自杀还是被俘，最终决定自杀，并以抽签的方式决定谁杀掉谁。约瑟夫斯和另外一个人是最后两个留下的人。约瑟夫斯说服了那个人，他们将向罗马军队投降，不再自杀。约瑟夫斯把他的存活归因于运气或天意，他不知道是哪一个。 —— 【约瑟夫问题】维基百科

方法

数学+递归

思路
题目中的要求可以表述为：给定一个长度为n的序列，每次向后数m个元素并删除，那么最终留下的是第几个元素？
有拆分为较小子问题的潜质：如果我们知道对于一个长度n-1的序列，留下的是第几个元素，那么我们就可以由此计算出长度为n的序列的答案。
算法
我们将上述问题建模为函数f(n, m)，该函数的返回值为最终留下的元素的序号。
首先，长度为n的序列会先删除第m % n个元素，然后剩下一个长度为n-1的序列。那么，我们可以递归地求解fn(n - 1, m)，就可以知道对于剩下的n -1 个元素，最终会留下第几个元素，我们设答案为x = f(n-1, m)。
由于我们删除了第m % n个元素，将序列的长度变为n-1。当我们知道了f(n-1, m)对应的答案x之后，我们就可以知道，长度为n的序列最后一个删除的元素，应当是从m%n开始数的第x个元素，因此有f(n, m) = ( m % n + x) % n = (m + x) % n

我们有n个数，下标从0到n-1，然后从index=0开始数，每次数m个数，最后看能剩下谁。我们假设能剩下的树的下标为y，则我们把这件事表示为 f(n, m) = y 这个y到底表示了啥呢？注意，y是下标，所以就意味着你从index=0开始数，数y+1个数，然后就停，停谁身上谁就是结果。 我们假设f(n-1, m) = x，然后来找一找f(n, m)和f(n-1,m)到底啥关系 f(n -1, m) = x意味着啥呢，意味着有n - 1个数的时候从index=0开始数，数x + 1个数就找到这结果了。那我不从index=0开始数呢？比如我从index=i开始数呢？那很简单，你把上面的答案也往后挪i下，就得到答案了。当然了，你要是挪到末尾了你就取个余，从头接着挪。

于是我们来思考f(n, m)时考虑以下两件事：

  1. 有n个数的时候，要划掉一个数，然后就剩n-1个数了，那划掉的这个数，下标是多少？
  2. 划完了这个数，往后数，数x+1个数，停在谁身上谁就是我们的答案。当然，数的过程中得取余

问题一：有n个数的时候，划掉了谁？下标是多少？ 因为要从0数m个数，那最后肯定落到了下标为m-1的数身上了，但这个下标可能超过我们有的最大下标（n-1）了，所以攒满n个就归零接着数，逢n归零，所以要模n。 所以有n个数的时候，我们划掉了下标为(m - 1) % n的数字。 问题二：我们划完了这个数，往后数x+1下，能落到谁身上呢，它的下标是几？ 你往后数x+1，它下标肯定变成了(m-1) % n + x + 1，和第一步的想法一样，你肯定还是得取模，所以答案为[(m - 1) % n + x + 1] % n，则 f(n, m) = [(m - 1) % n + x + 1] % n，其中x = f(n - 1, m)

我们化简它 定理一：两个正整数a, b的和，模另外一个数c，就等于它俩分别c，模完之后加起来再模 (a + b) % c = ((a % c) + (b % c)) % c 定理二：一个正整数a, 模c，模一遍和模两边是一样的 a % c = (a % c) % c

所以 f( n, m) = [(m - 1) % n + x + 1] = [(m - 1) % n % n + (x + 1) % n] % n = [( m - 1) % n + (x + 1) % n] % n = (m - 1 + x + 1) % n = ( m + x) % n 因此有f(n, m) = (m + x) % n

我们递归计算f(n, m), f(n - 1, m), f(n - 2, m), … 直到递归的重点f(1, m)。
当序列长度为1时，一定会留下唯一的那个元素，它的编号为0

  1. /**
  2.  * @param {number} n
  3.  * @param {number} m
  4.  * @return {number}
  5.  */
  6. var lastRemaining = function(n, m) {
  7.   return f(n, m);
  8. };
  10. function f(n, m) {
  11.   if (n == 1) {
  12.     return 0;
  13.   }
  14.   const x = f(n - 1, m);
  15.   return (m + x) % n;
  16. }

复杂度分析

  • 时间复杂度：O(n)，需要求解的函数值有n个。
  • 空间复杂度：O(n)，函数的递归深度为n，需要使用O(n)的栈空间。

    ⭐️数学+迭代

    思路
    上面的递归可以改写为迭代，避免递归使用栈空间。
    算法
    约瑟夫环问题，是有数学解法的。
    因为数据是放在数组里，所以在数组后面加上数组的复制，以体现是环状的。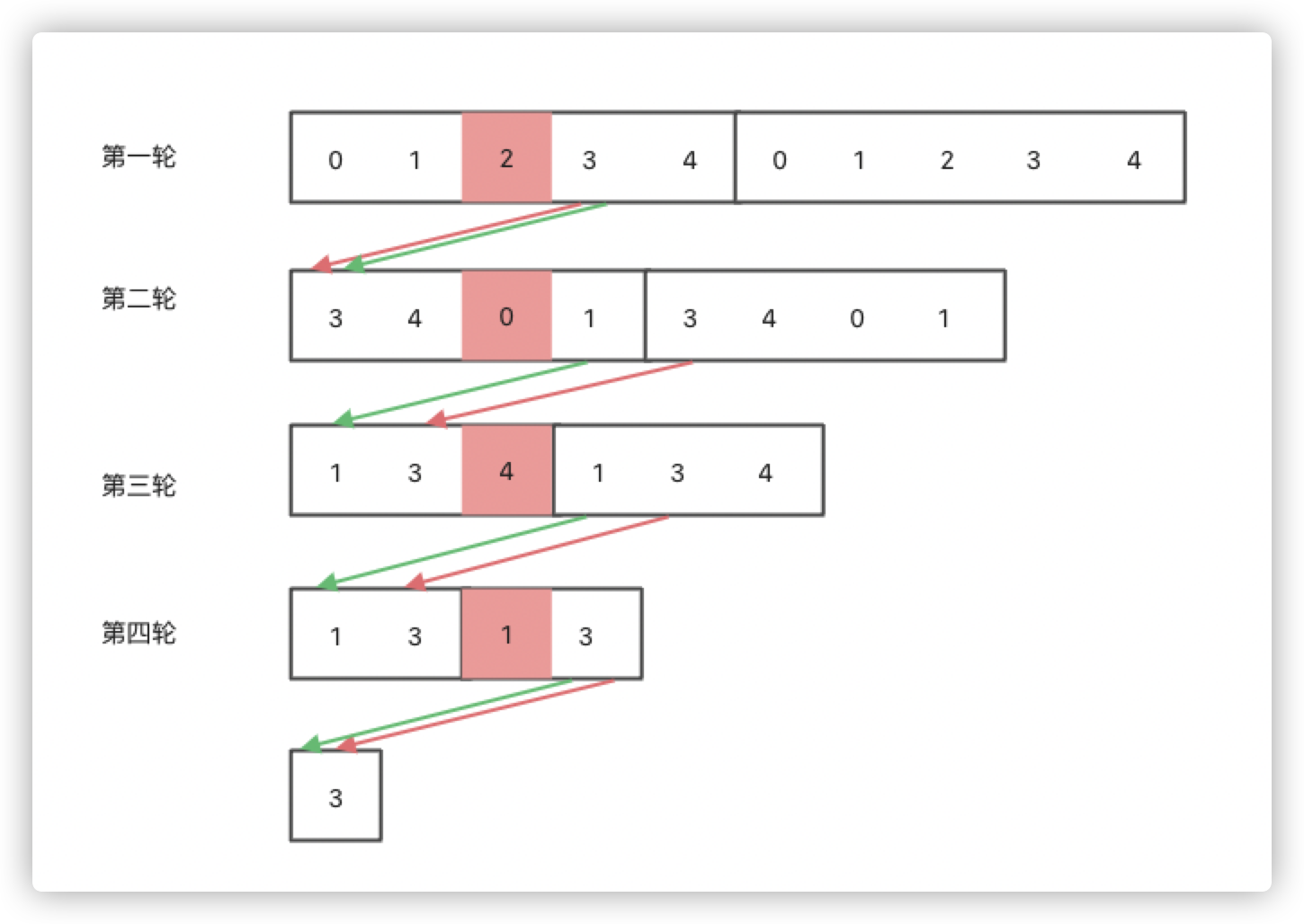
    image.png
    我们每次删除的是第m个数字，都已经标红。
    第一轮是 [0, 1, 2, 3, 4] ，所以是 [0, 1, 2, 3, 4] 这个数组的多个复制。这一轮 2 删除了。
    第二轮开始时，从 3 开始，所以是 [3, 4, 0, 1] 这个数组的多个复制。这一轮 0 删除了。
    第三轮开始时，从 1 开始，所以是 [1, 3, 4] 这个数组的多个复制。这一轮 4 删除了。
    第四轮开始时，还是从 1 开始，所以是 [1, 3] 这个数组的多个复制。这一轮 1 删除了。
    最后剩下的数字是 3。

图中的绿色的线指的是新的一轮的开头是怎么指定的，每次都是固定地向前移位 m 个位置。（为什么要右移m个位置。因为，上一轮删除了第m个位置，索引从0开始。因此，本轮的索引0就是上一轮的索引m。如果从本轮的索引找回上一轮的索引，就要加m，最后加个溢出处理）。
然后我们从最后剩下的 3 倒着看，我们可以反向推出这个数字在之前每个轮次的位置。
最后剩下的 3 的下标是 0。
第四轮反推，补上 m 个位置，然后模上当时的数组大小 2，位置是(3 + 0) % 2 = 1。
第三轮反推，补上 m 个位置，然后模上当时的数组大小 3，位置是(3 + 1) % 3 = 1。
第二轮反推，补上 m 个位置，然后模上当时的数组大小 4，位置是(3 + 1) % 4 = 0。
第一轮反推，补上 m 个位置，然后模上当时的数组大小 5，位置是(3 + 1) % 5 = 3。
所以最终剩下的数字的下标就是3。因为数组是从0开始的，所以最终的答案就是3。

总结一下反推的过程，就是 (当前index + m) % 上一轮剩余数字的个数。

  1. /**
  2.  * @param {number} n
  3.  * @param {number} m
  4.  * @return {number}
  5.  */
  6. var lastRemaining = function(n, m) {
  7.   let last = 0;
  8.   // 最后一轮剩下2个，所以从2开始反推
  9.   for (let i = 2; i < n + 1; i++) {
  10.     last = (m + last) % i
  11.   }
  12.   return last
  13. };

复杂度分析

  • 时间复杂度：O(n)，需要求解的函数值有n个
  • 空间复杂度：O(1)，只使用常数个变量