题目一：给两个数组，一个从大到小排序，一个从小到大排序，找到最大的第k个数字image.png

题目二： 两个等长数组上中位数的问题
有两个从小到大排序的数组，求中位数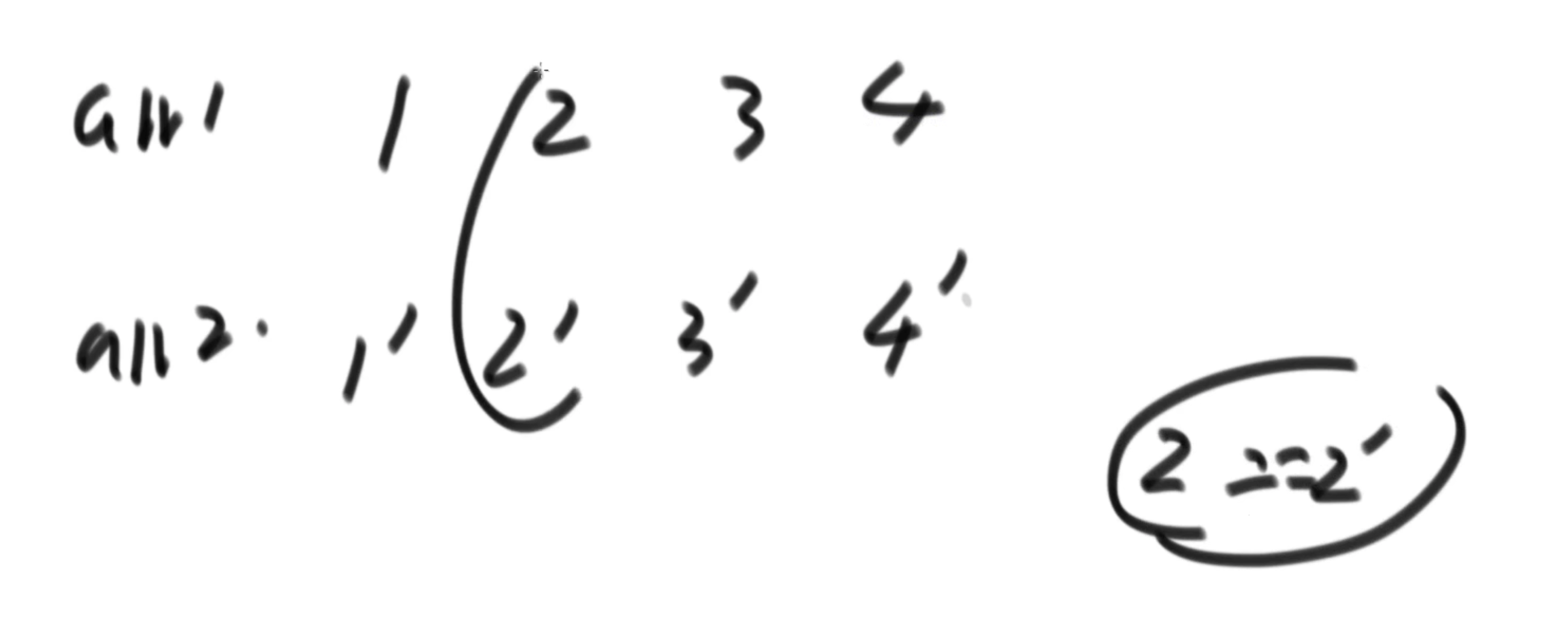
image.png
分析：
1、 如果两个数组等长且长度为偶数，分别看中位数，如果中位数相等，那么这个值就是整体的中位数，
因为每个数组小于这个值的都是一半。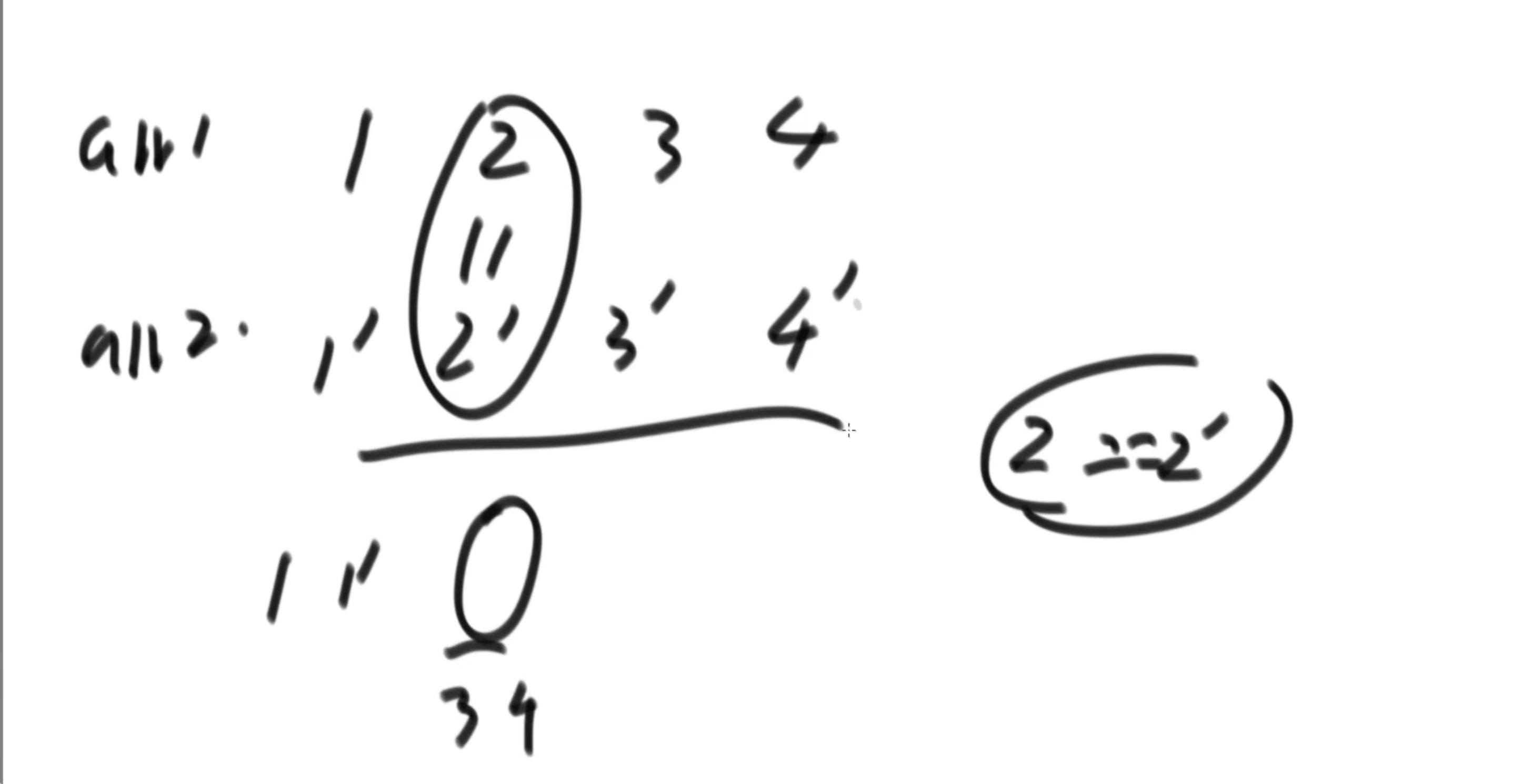
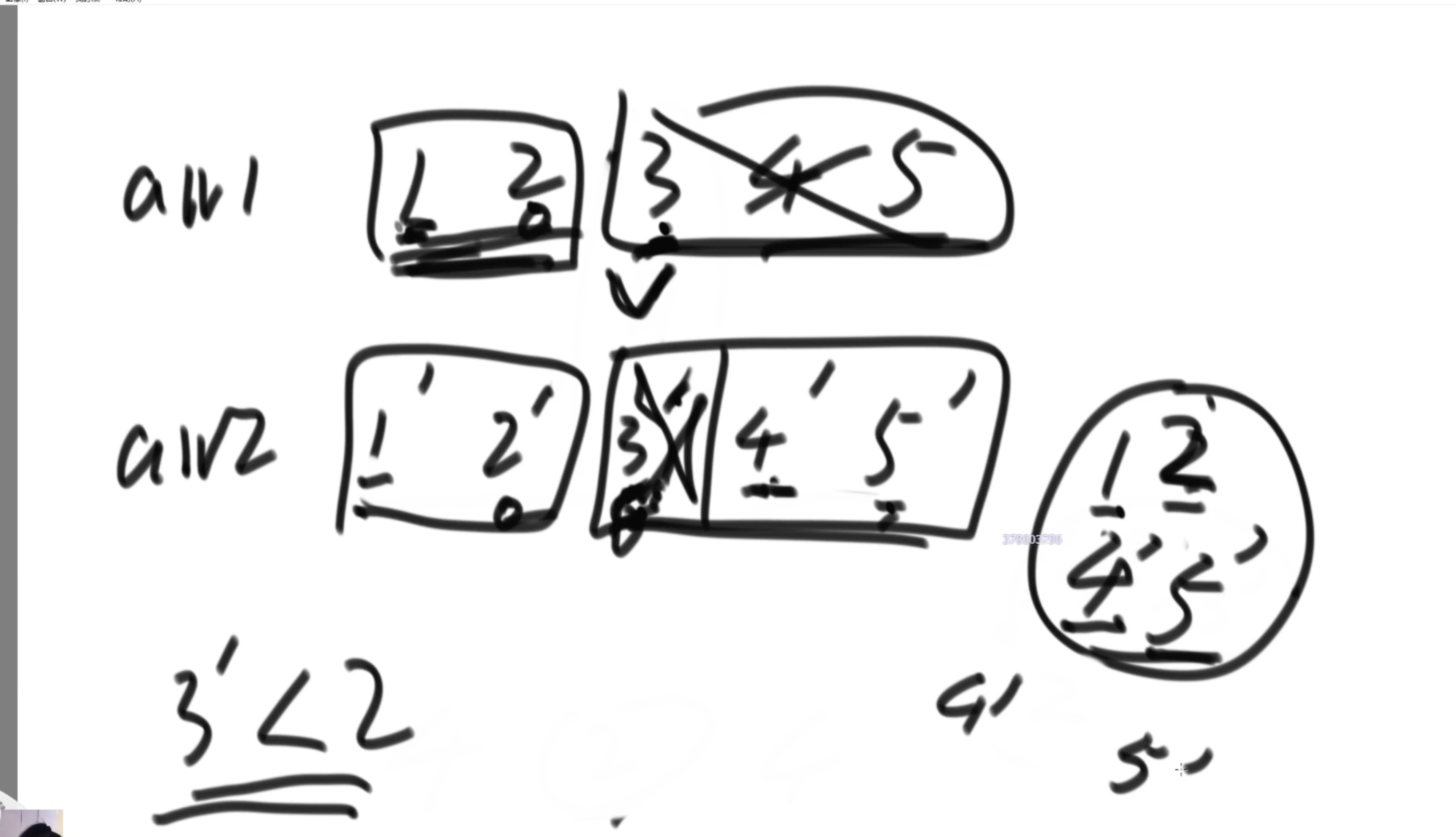
image.png
2、如果arr1 中的第二个位置的数字大于 arr2中的第二个位置的数，那么，较大值右侧的数字其左侧数量不少于 4个，所以3、4位置的值可以排除在目标范围外。然后需要分析
另一个2‘ 也可以排除，因为他至多排在第三位（前两位是1 和 1‘）
所以候选目标集合在1，2，3‘，4‘组成的集合中，4个值求上中位数，采用插入排序，求第二个位置的值，不麻烦吧。
3、不断递归这个过程，整个时间复杂度是logN，因为两个数组同时二分，然后不断比较中位数的大小，剩下的两部分继续递归求中位数。

假设数组是奇数的时候，

image.png
tips：图示数组只表示索引，不表示具体的数字。
step1: 同样的，如果3 位置的 和 3‘ 位置的相等，那么中位数就是该数字
step2：如果 3 位置的 大于3’位置的 首先3 不可能，因为他至少在第6个位置上。同样4，5也不可能
在考察3‘左边的数字，2‘最多超过2，排在第4位，少于整体一半位置，所以也不可能。
思考：就相当于两个门派里面，找武力居中的人，第一个门派的3师兄超过第二个门派的三师兄，那么武力值排第五的人要从第一个门派里面的小字辈和第二个门派里面的更大辈进行比较。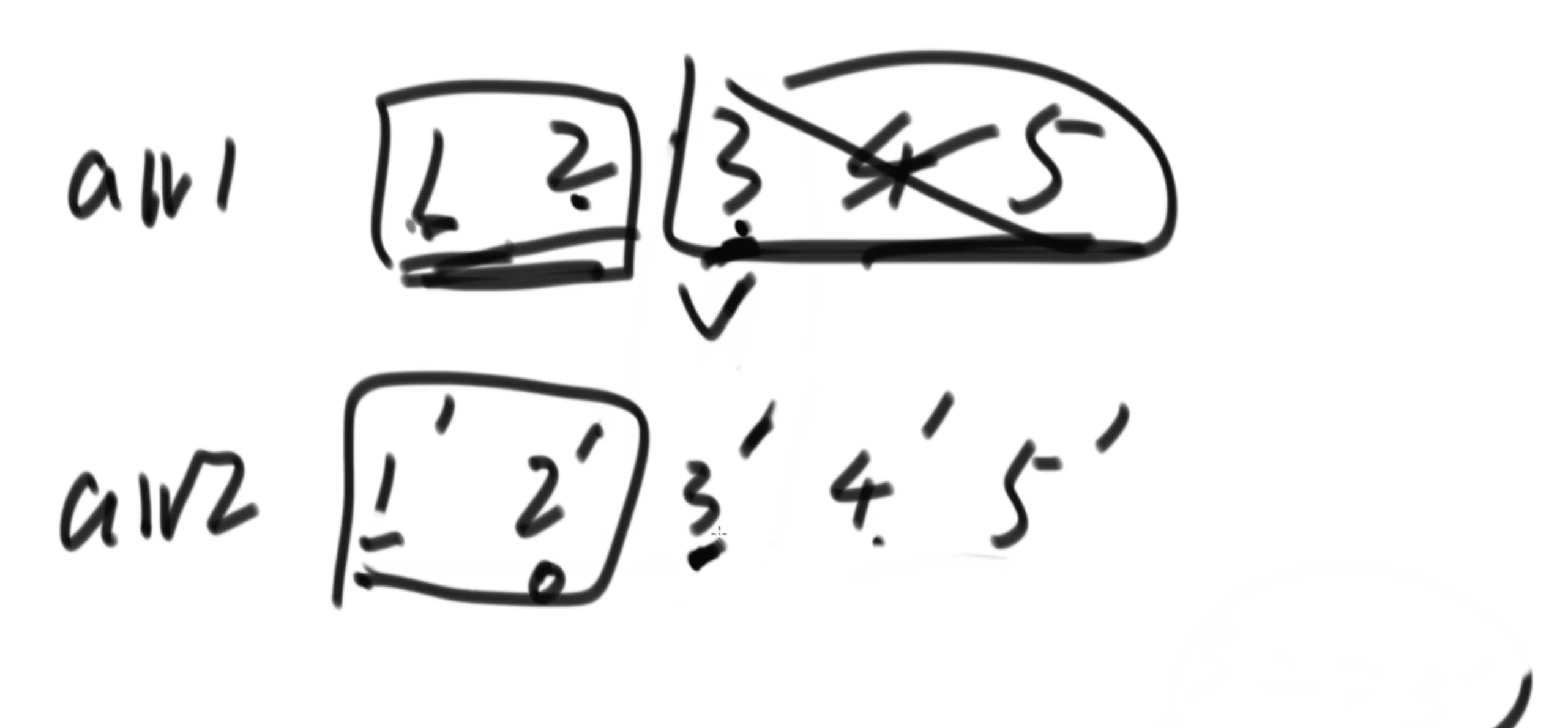
image.png
这样筛选区间在12，3‘4’5‘ 组成的集合中，但是这样两个子数组不等长了，但是观察到只相差一位，所以手动比较一个2 和 3‘
如果3’>2(相等也可以)，那么3就是目标值，否则，移除3‘，对12 和 3’4‘5’两个子数组进行递归。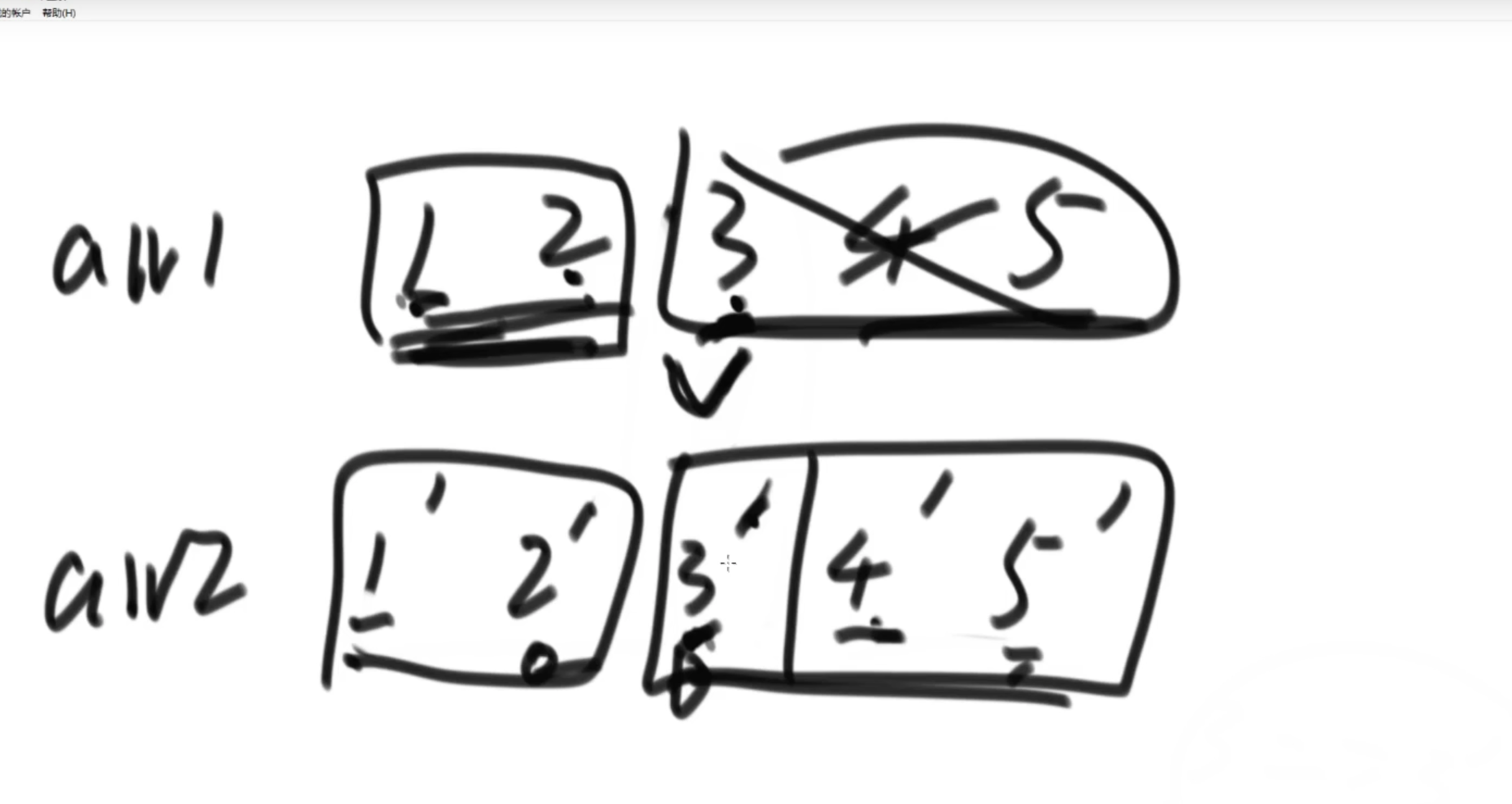
image.png
step4: 这样，分析最后剩余的4个元素，不管谁是第二小的数，都能处在一半的位置上
所以，不管两个原数组长度是奇数还是偶数，只要等长，就一定能在O（logN）的时间内求出中位数。

  • 等长
  • 有序
  • 上中位数有传递性。

image.png

当长度不相等的时候，求第k小的数

情况1： 如果k小于较小数组的长度，那么就分别取1～k的长度，求中位数
image.png
情况2: 当k大于了长数组的长度，下图中的情况3；
假设求第23小的数
image.png
step1：排除不可能的区域，可以发现跟k和两个数组长度有关系。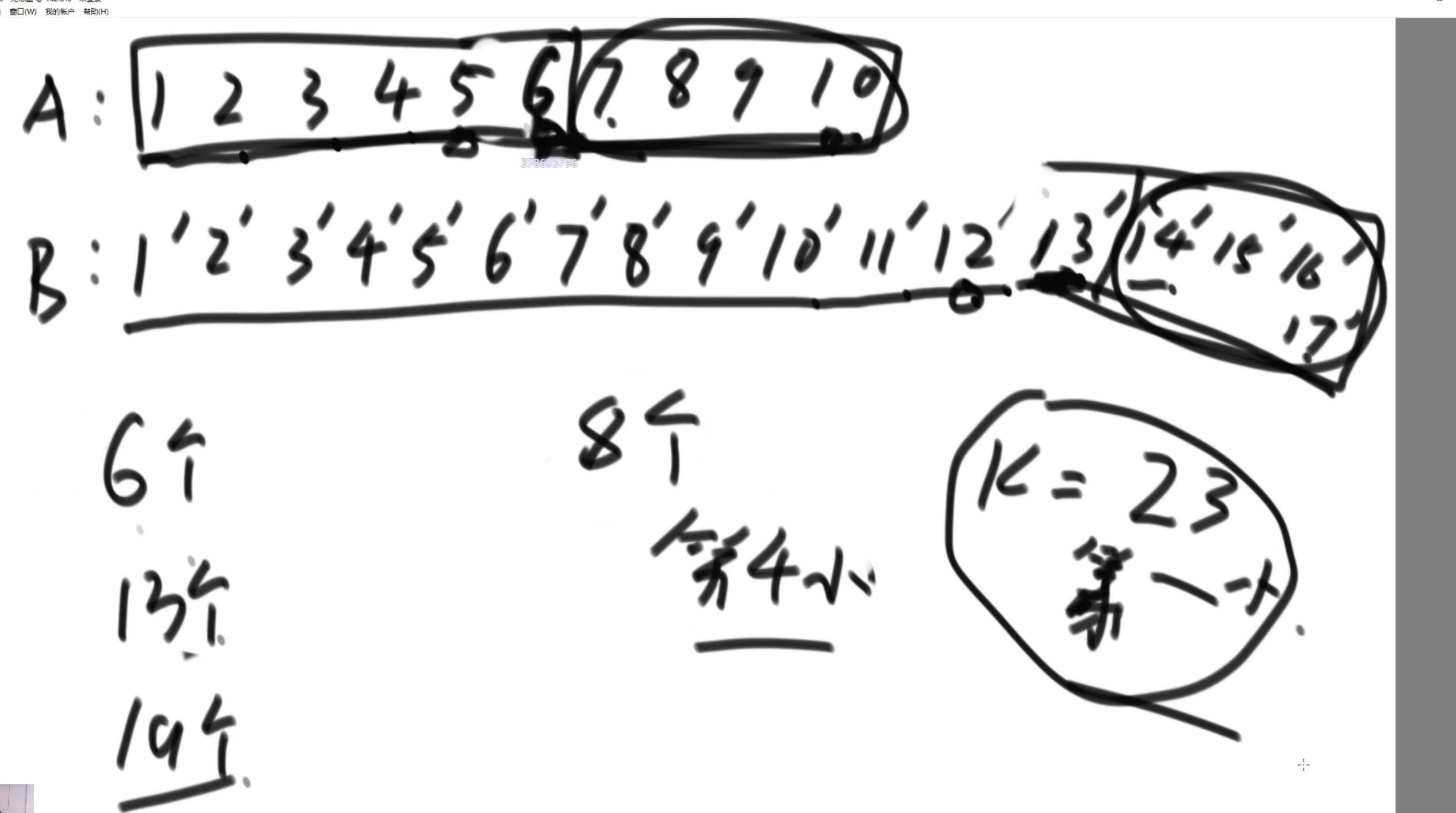
image.png
step2: 剩余的可选空间，如果求中位数的话，不管在哪个区域求的都是第22小的区域，所以需要多比较两次，将不可选区域扩展两位

  • 比较6 和 17‘的大小，如果6>17’ 那么6就是目标值，如果不是，6不可选
  • 同理比较10 和13‘，如果13’大于10位置的数，那么13‘就是目标值，如果不是13’不可选
  • 如果6和13‘都不可选，那么剩余的区域求中位数（即第四位）就是目标值。

思考：

  • 这种策略总结一下就是，原来两个不可选区域是 5 和 12’， 可选区域中位数排第5，对于结论少了一个数，如果不可选区域总长度+2， 可选区域目标位置-1，正好就比原来多了一位，取到第23的位置。
  • 像这种人为验证来过滤不可选区域的方法，在一下有相等元素扰乱二分过程的场景中有些应用。

情况3: k大于短数组长度，小于长数组长度。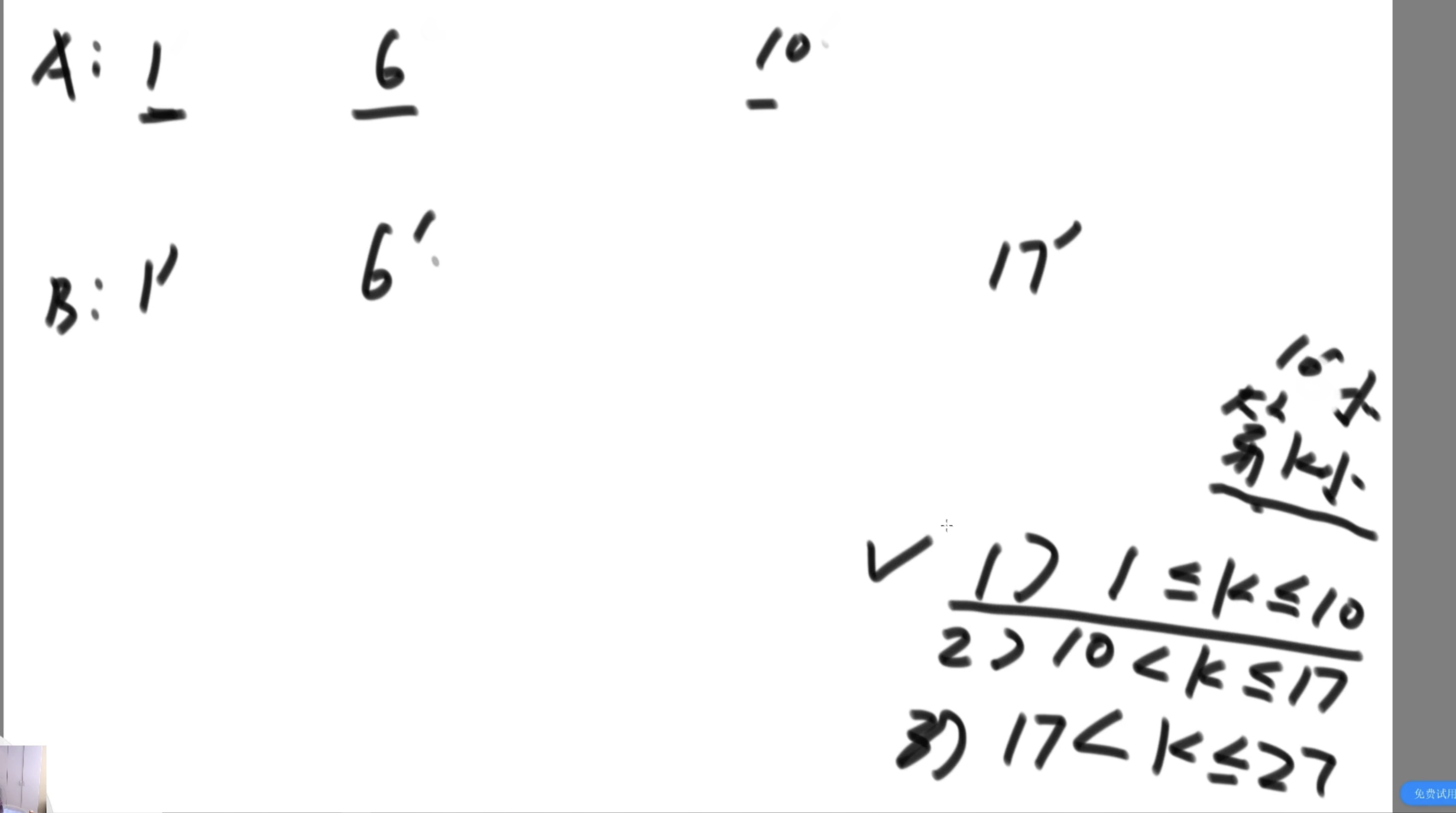
image.png
例子，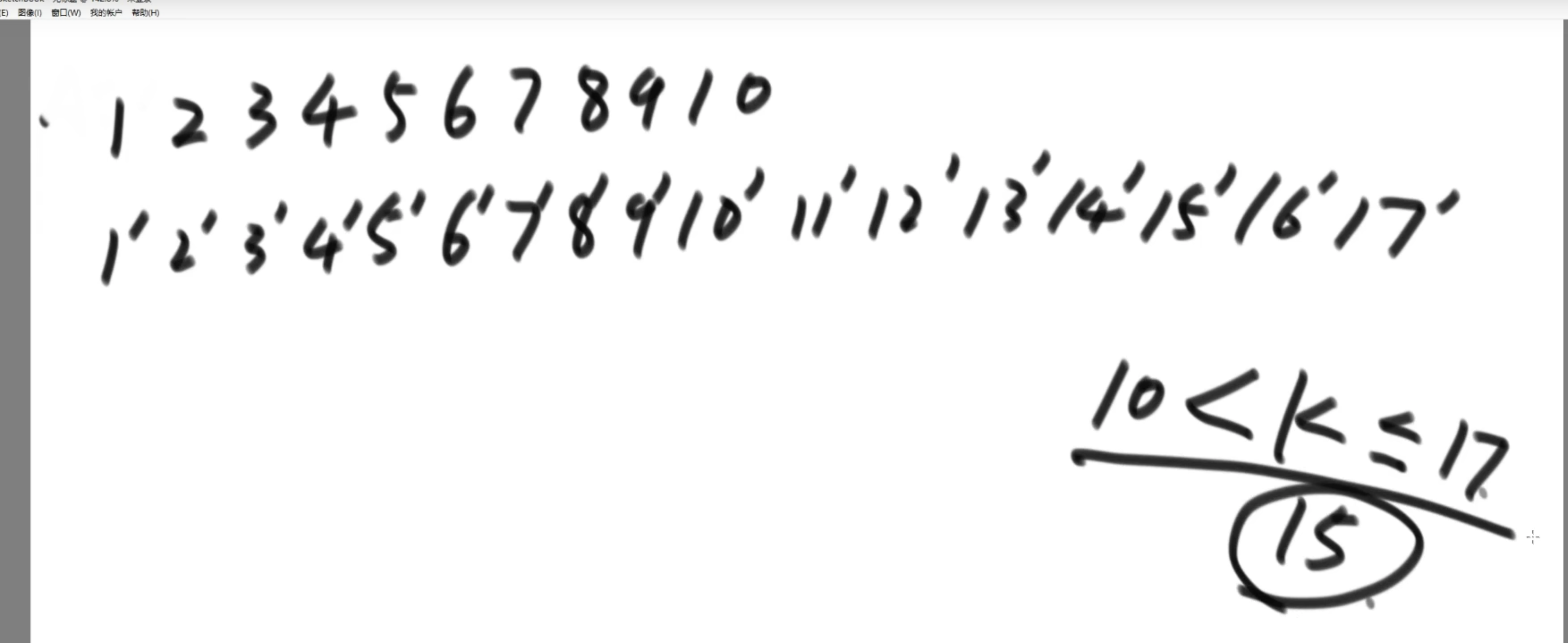
image.png
step1:看那些元素属于不可选区域。

  • 下面的1‘到4’
  • 16‘和17也不可选，因为至少是排在16和17位
  • 短数组的所有值都有可能

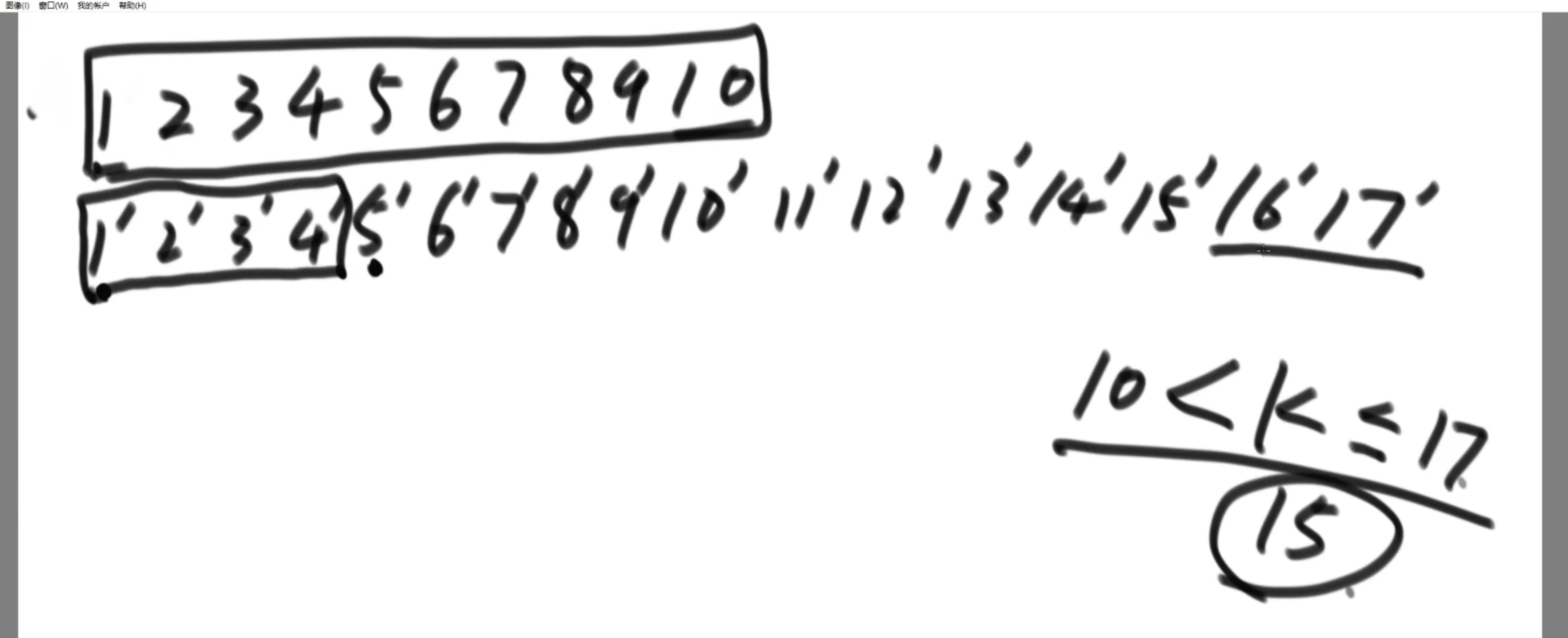
image.png
step2：剩下的可选区域长度分别是10 和 11， 所以，也需要一次额外的比较，将可选区域变成等长
然后取可选区域的中位数，再看剩余不可选区域与目标位置是否正好达到预期，这个例子中，不可选的前面是5个，加上后面的第十位，正好是第15位。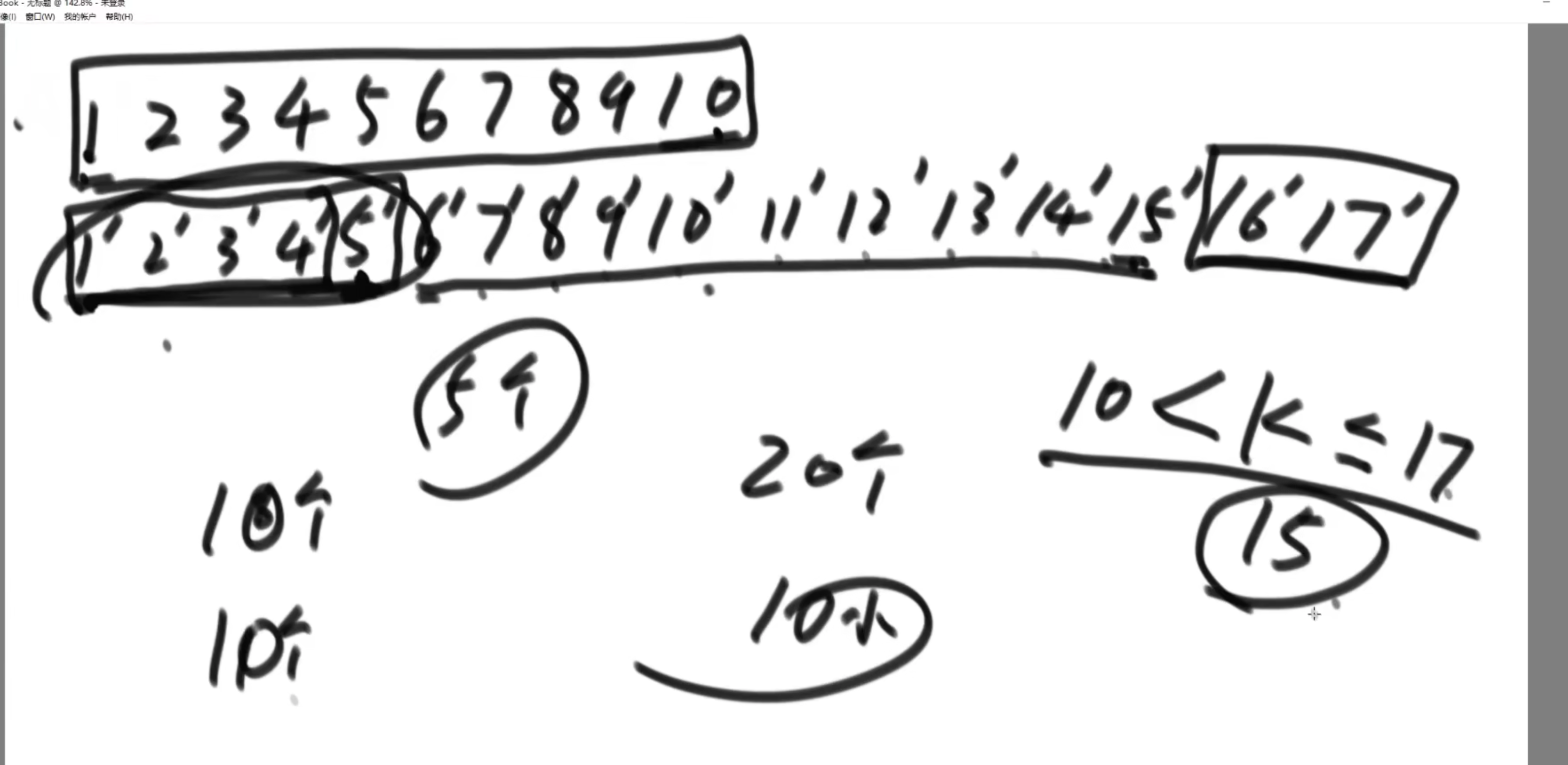
image.png
代码中难点和易错点是下标变换
LeetCode4 有一道有求中位数的题，考虑了中位数数学定义，即：如果数组总长度是偶数，那么中位数是两个中间元素的平均值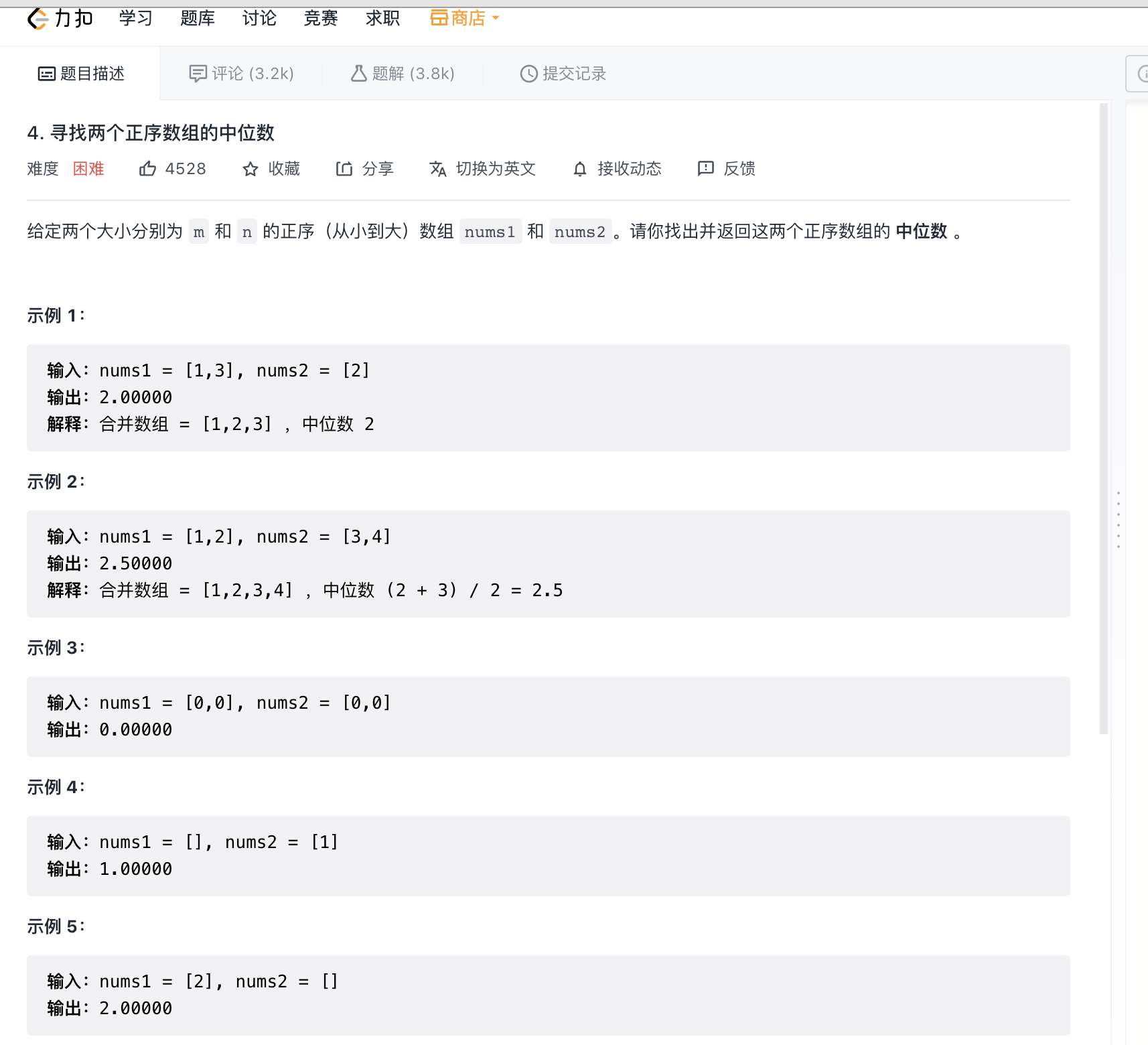
image.png
我的解法是根据左的思路，通过对比k和两个数组长度的关系来分类分析的。但是当总长度为偶数的时候，我是采用两遍查询来找中间两个数，所以增加了一倍的RunTime，如果优化，要再看看官网的题解
image.png
我的代码：核心代码130行，有点长，官网题解十分精炼

  1.    public static void main(String[] args) {
  2.         int[] arr1 = {1,3,4,5};
  3.         int[] arr2 = {1,2,3,4};
  4.         System.out.println(s(arr1, 0, 3, arr2, 0, 3));
  6.         int [] arr3 = {1,2,3};
  7.         int[] arr4 = {1,2,3,4,5,6};
  8.         System.out.println(process(arr3, arr4, 5));
  9.         System.out.println(process(arr3, arr4, 8));
  10.         System.out.println(process(arr3, arr4, 3));
  12.         System.out.println(findMedianSortedArrays(null, arr4));
  13.         System.out.println(findMedianSortedArrays(arr3, null ));
  16.         System.out.println("-------------------");
  17.         int[] arr5 = {1};
  18.         int[] arr6 = {2,3};
  19.         System.out.println(findMedianSortedArrays(arr5, arr6));
  20.         System.out.println(getMid(1, 2, 3, 4));
  22.     }
  24.     public static double getAverage( int[] nums1, int[] nums2){
  25.         int l1 = nums1.length;
  26.         int l2 = nums2.length;
  27.         /**如果总长度是偶数*/
  28.         if(((l1 +l2) & 1) == 0){
  29.             int p1 = process(nums1, nums2, (l1 +l2)>>1-1);
  30.             int p2 = process(nums1, nums2, (l1 +l2)>>1);
  31.             return (p1 + p2) /2;
  32.         }
  33.         else return  process(nums1, nums2, (l1 +l2)>>1 +1);
  34.     }
  35.     public static double findMedianSortedArrays(int[] nums1, int[] nums2) {
  36.         if((nums1 == null || nums1.length == 0) && nums2.length != 0) {
  37.             return getMid(nums2);
  38.         }
  39.         if( (nums2 == null || nums2.length == 0) && nums1.length!=0){
  40.             return getMid(nums1);
  41.         }
  42.         int l1 = nums1.length;
  43.         int l2 = nums2.length;
  44.         /**如果总长度是偶数*/
  45.         if(((l1 +l2) & 1) == 0){
  46.             int p1 = process(nums1, nums2, ((l1 +l2)>>1));
  47.             int p2 = process(nums1, nums2, ((l1 +l2)>>1)+1);
  48.             return (p1 + p2) /2.0;
  49.         }
  50.         else return  process(nums1, nums2, ((l1 +l2)>>1) +1);
  51.     }
  52.     /**当另一个数组是空，或者没有元素的时候，获取非空数组的中位数*/
  53.     public static double getMid(int[] nums1){
  54.         if(nums1.length == 1) return nums1[0];
  55.         if((nums1.length & 1) == 0){
  56.             return (nums1[nums1.length/2 -1] + nums1[nums1.length/2]) /2.0;
  57.         }else {
  58.             return   nums1[nums1.length/2];
  59.         }
  60.     }
  61.     public static int process(int[] nums1, int[] nums2 ,int k ){
  62.         int l1 = nums1.length;
  63.         int l2 = nums2.length;
  64.         int small = l1 < l2? l1: l2;
  65.         int big = small == l1 ? l2 :l1 ;
  67.         int[] smaller = small == nums1.length ? nums1: nums2;
  68.         int[] bigger = smaller == nums1 ? nums2: nums1;
  69.         if(k<= small) return s(nums1, 0, k-1 , nums2, 0 , k-1 );
  70.         if(k > big) {
  71.             int m = k- small;
  72.             int n = k - big;
  73.             if(bigger[m-1] > smaller[small-1]) {
  74.                 return bigger[m-1];
  75.             }
  76.             if(bigger[big-1]< smaller[n-1] ){
  77.                 return smaller[n-1];
  78.             }
  79.             return s(smaller, n , small-1, bigger, m, big-1 );
  80.         }
  81.         else {
  82.             int m = k-small;
  83.             if(bigger[m-1] >= smaller[small-1]) return bigger[m-1];
  84.             else {
  85.                 return s(smaller, 0 , small-1, bigger, m,k-1);
  86.             }
  87.         }
  88.     }
  89.     public static int s(int[] nums1, int i, int j, int[] nums2, int p, int q){
  90.         if(j-i == 0 && q-p == 0) return nums1[i] < nums2[p] ? nums1[i] : nums2[p];
  91.         if((j-i ==1) && (q-p == 1)){
  92.             return getMid(nums1[i], nums1[j],nums2[p],nums2[q]);
  93.         }
  94.         int mid1 = i + (((j-i)>>1));
  95.         int mid2 = p + (((q-p)>>1));
  96.         if(nums1[mid1] == nums2[mid2]){
  97.             return nums1[(i+j)>>1];
  98.         }
  99.         int[] greater = nums1[mid1] > nums2[mid2]? nums1: nums2;
  100.         int[] smaller = greater == nums1 ? nums2 : nums1;
  101.         if(greater == nums2){
  102.             int temp = mid1;
  103.             mid1 = mid2;
  104.             mid2= temp;
  105.             temp = i;
  106.             i = p;
  107.             p = temp;
  108.             temp = j;
  109.             j = q;
  110.             q= temp;
  111.         }
  112.         int res = -1;
  113.         if(((j-i) & 1) !=0){
  114.             res = s(greater, i, mid1, smaller,mid2+1, q);
  115.         }else {
  116.             if(greater[mid1-1] < smaller[mid2]){
  117.                 res =  smaller[mid2];
  118.             }
  119.             else {
  120.                 res = s(greater, i,mid1-1, smaller, mid2+1,q);
  121.             }
  122.         }
  123.         return res;
  124.     }
  126.     public  static int getMid(int a, int b, int c, int d) {
  127.         int[] arr = new int[4];
  128.         arr[0] = a;
  129.         arr[1] = b;
  130.         arr[2] = c;
  131.         arr[3] = d;
  132.         for (int i = 1; i < arr.length; i++){
  133.            for(int j = i; j >0 && arr[j] < arr[j-1] ; j--){
  134.                swap(arr, j, j-1);
  135.            }
  136.         }
  137.         return arr[1];
  138.     }
  139.     public static void swap(int[] arr ,int i , int j ){
  140.         int temp = arr[i];
  141.         arr[i] = arr[j];
  142.         arr[j] =temp;
  143.     }

解法二：
分割线法
核心思想

  • 就是让分割线左边的元素达到要求，分奇偶情况，偶数正好一半，奇数一半多一个。
  • 当我们获取到一条分割线的时候只有下面这两种情况，第二个数组左边元素大于第一个数组右边元素

或者第一个数组左边元素大于第二个数组右边元素，同时如果任何一种情况，另一个对角线是肯定满足合法关系的。

  • 中位数的索引肯定居于短数组 和 长数组 长度中间，就相当于上面左程云解法的第二种情况，为了保证遍历时间短 和 分割线左右两边有元素用于比较，决定从小数组开始遍历

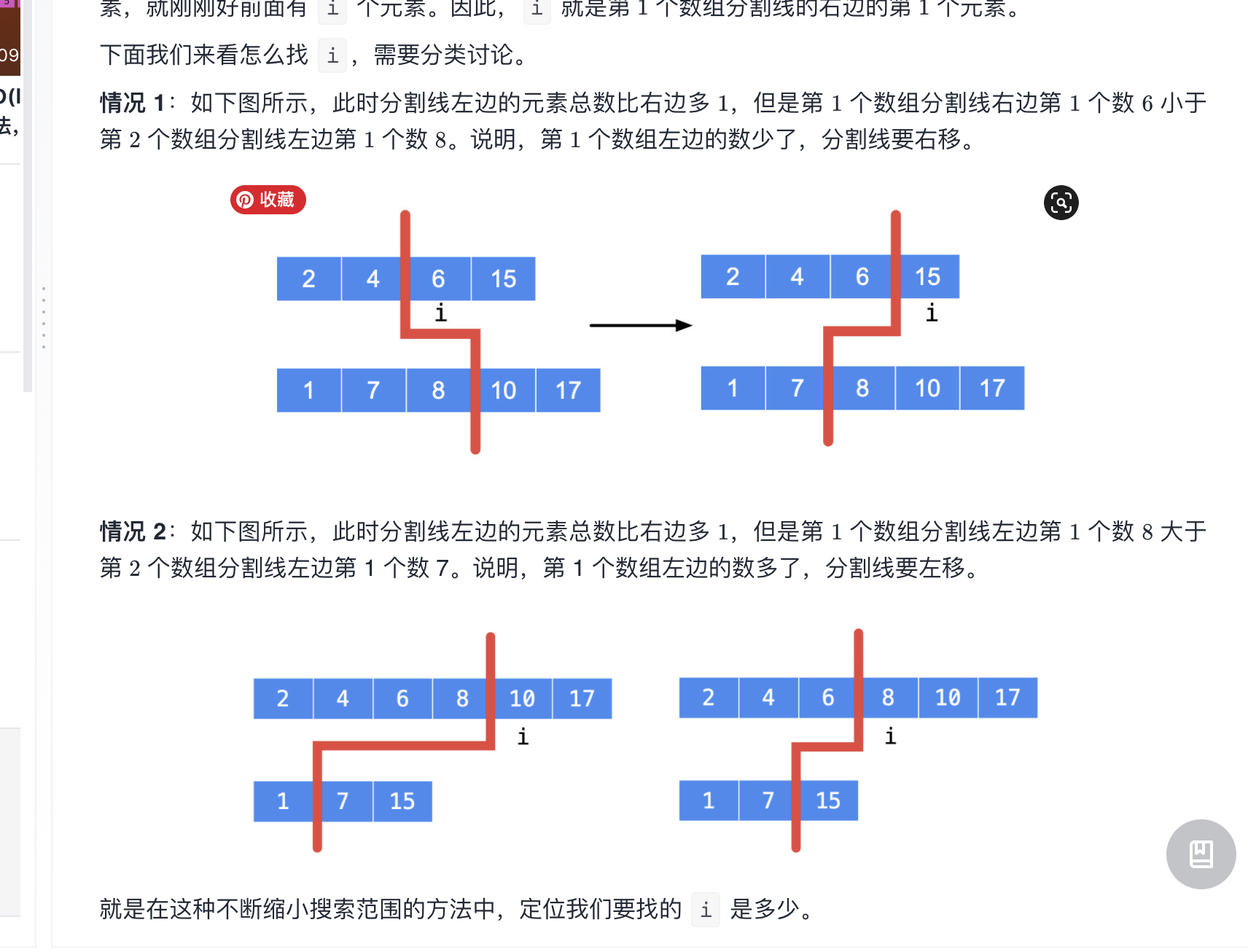
image.png
代码：

  public static void main(String[] args) {
        int[] arr1= {1,2};
        int[] arr2= {3,4};

        System.out.println(findMedianSortedArrays(arr1, arr2));
    }
    public static double findMedianSortedArrays(int[] nums1, int[] nums2) {
        if(nums1.length > nums2.length){
            int[] temp = nums1;
            nums1 = nums2;
            nums2 = temp;
        }
        int l1 = nums1.length;
        int l2 = nums2.length;
        int totalLeft = (l1 + l2 + 1 ) /2;
        /**分割线在左侧集合的右边，所以，最小值就是0的位置，最大值在长度的区域*/
        int left = 0;
        int right = l1;
        /**取中线的时候，如果left和 right相差1，下面这种计算是获取的左边*/
        //int mid = left + (right-left )/2;
        /**，如果要保证分割线的左侧有元素，那么就要 采用上取整的方式，使分割线每次靠近右边界*/

        while(left < right){
            int mid = left+ (right - left +1) / 2;
            int remain = totalLeft - mid;
            if(nums1[mid-1] > nums2[remain]){
                right = mid-1;
            }else {
                left = mid ;
            }
        }

        int i = left;
        int j = totalLeft - i;
        int nums1LeftMax = i == 0 ? Integer.MIN_VALUE : nums1[i-1];
        int nums1RgithMin = i == l1 ? Integer.MAX_VALUE: nums1[i];
        int nums2LeftMax = j == 0 ? Integer.MIN_VALUE : nums2[j-1];
        int nums2RightMin = j == l2? Integer.MAX_VALUE : nums2[j];

        /**偶数*/
        if( ((l1 + l2) & 1)  == 0){
            return (Math.max(nums1LeftMax, nums2LeftMax) + Math.min(nums1RgithMin, nums2RightMin) )/2.0;
        }else {
            return Math.max(nums1LeftMax, nums2LeftMax);
        }

    }

tips：
1、以短数组为参考对象，分割线的索引是左侧集合的下一个元素，所以取值范围是0～arr1.length
2、在获取中间轴的索引时，要保证短数组分割线左侧有元素用于比较，所以采用靠右取轴的方式
int mid = left+ (right - left +1) / 2;
与此对应，在缩减右侧搜索区域的条件下要mid-1。因为上面靠右取轴的方式在只有两个元素的时候是取右边的元素，通过mid-1，能够正确跳出循环。left<right;