Skip Lists 跳跃表（Pugh，1989）

a simple, randomized, efficient dynamic search structrue
Maintains a dynamic set of n elements in O(lgn) time per operation in expectation an with high probability (w.h.p)”almost always”

one linked list

Start from simplest data structure: (sort) linked list

• Searches take O(n) time in worst case
• How can we speed up searches?

Two linked lists

Suppose we had two sorted linked lists (on subsets of the elements).

• Each element can appear in one or both lists
• How can we speed up searches?

IDEA : 类似客车的快线与慢线

• Express line connects a few of the stations
• Local line connects all stations
• Links between lines at common stations

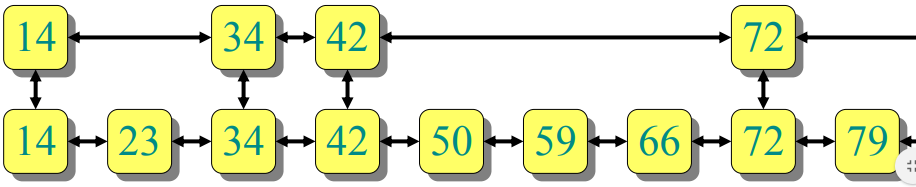
Searching in two linked lists

SEARCH(x)
    Walk right in top linked list(L1) until going right would go too far
  Walk down to bottom linked list(L2)
  Walk right in L2 until element found(or not)

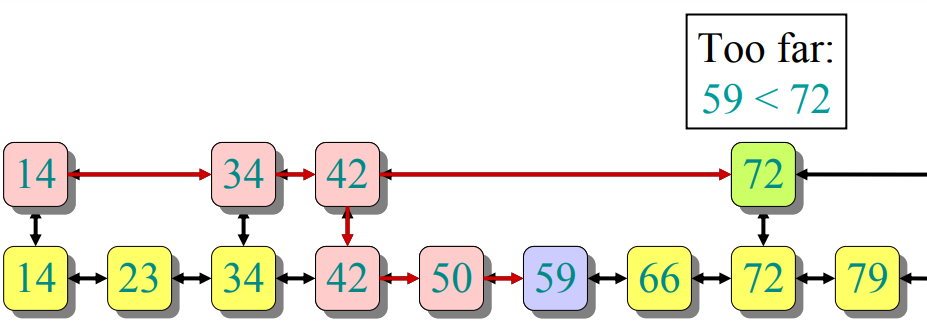
Question : Which nodes should be in L1?

• In a subway, the “Popular stations”
• Here we care about worst-case performance
• Best approach : Evenly space the nodes in L1
• But how many nodes should be in L1

Analysis
Search cost is roughly |L1|+|L2|/|L1|
Minimized(up to constant factors) when terms are equal: , and Search cost is roughly

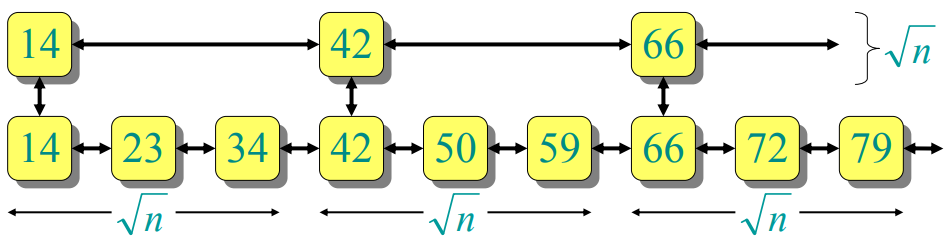
More linked lists

What if we had more sorted linked lists?

• 2 sorted lists
• 3 sorted lists
• k sorted lists
• lgn sorted lists

lgn sorted linked lists are like a binary tree .

insert(x) and delete(x)

Skip list data structure maintains roughly this structure subject to updates (insert/delete)

To insert an element x into a skip list:

• SEARCH(x) to see where x fits in bottom list
• Always insert into bottom list

INVARIANT : Bottom list contains all elements , insert into some of the lists above…
QUESTION : To which other lists should we add x?
IDEA : Flip a (fair) coin ; if HEADS, promote x to next level up and flip again
Probability of promotion to next level = 1/2
Small changes : Add special −∞ value to every list ⇒ can search with the same algorithm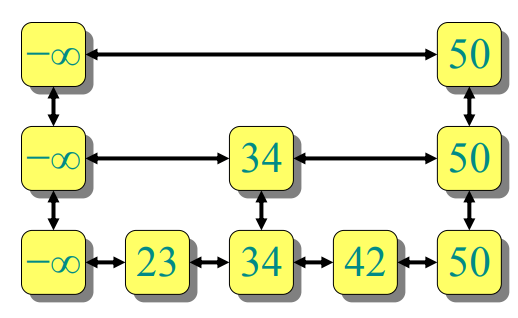

How good are skip lists? (speed/balance)

INTUITIVELY : Pretty good on average
CLAIM : Really, really good, almost always

THEOREM : With high probability, every search in an n-element skip list costs O(lgn)
证明略
LEMMA : With high probability, n-element skip list has O(lgn) levels
证明略
CLAIM : Number of coin flips until c lgn HEADs = Θ(lgn) with high probability

/***************************  SkipList.java  *********************/

import java.util.Random;

public class SkipList<T extends Comparable<? super T>> {
    private int maxLevel;
    private SkipListNode<T>[] root;
    private int[] powers;
    private Random rd = new Random();
    SkipList() {
        this(4);
    }
    SkipList(int i) {
        maxLevel = i;
        root = new SkipListNode[maxLevel];
        powers = new int[maxLevel];
        for (int j = 0; j < maxLevel; j++)
            root[j] = null;
        choosePowers();
    }
    public boolean isEmpty() {
        return root[0] == null;
    }
    public void choosePowers() {
        powers[maxLevel-1] = (2 << (maxLevel-1)) - 1;    // 2^maxLevel - 1
        for (int i = maxLevel - 2, j = 0; i >= 0; i--, j++)
           powers[i] = powers[i+1] - (2 << j);           // 2^(j+1)
    }
    public int chooseLevel() {
        int i, r = Math.abs(rd.nextInt()) % powers[maxLevel-1] + 1;
        for (i = 1; i < maxLevel; i++)
            if (r < powers[i])
                return i-1; // return a level < the highest level;
        return i-1;         // return the highest level;
    }
    // make sure (with isEmpty()) that search() is called for a nonempty list;
    public T search(T key) {
        int lvl;
        SkipListNode<T> prev, curr;            // find the highest nonnull
        for (lvl = maxLevel-1; lvl >= 0 && root[lvl] == null; lvl--); // level;
        prev = curr = root[lvl];
        while (true) {
            if (key.equals(curr.key))          // success if equal;
                 return curr.key;
            else if (key.compareTo(curr.key) < 0) { // if smaller, go down,
                 if (lvl == 0)                 // if possible
                      return null;
                 else if (curr == root[lvl])   // by one level
                      curr = root[--lvl];      // starting from the
                 else curr = prev.next[--lvl]; // predecessor which
            }                                  // can be the root;
            else {                             // if greater,
                 prev = curr;                  // go to the next
                 if (curr.next[lvl] != null)   // non-null node
                      curr = curr.next[lvl];   // on the same level
                 else {                        // or to a list on a lower level;
                      for (lvl--; lvl >= 0 && curr.next[lvl] == null; lvl--);
                      if (lvl >= 0)
                           curr = curr.next[lvl];
                      else return null;
                 }
            }
        }
    }
    public void insert(T key) {
        SkipListNode<T>[] curr = new SkipListNode[maxLevel];
        SkipListNode<T>[] prev = new SkipListNode[maxLevel];
        SkipListNode<T> newNode;
        int lvl, i;
        curr[maxLevel-1] = root[maxLevel-1];
        prev[maxLevel-1] = null;
        for (lvl = maxLevel - 1; lvl >= 0; lvl--) {
            while (curr[lvl] != null && curr[lvl].key.compareTo(key) < 0) {
                prev[lvl] = curr[lvl];           // go to the next
                curr[lvl] = curr[lvl].next[lvl]; // if smaller;
            }
            if (curr[lvl] != null && key.equals(curr[lvl].key)) // don't
                return;                          // include duplicates;
            if (lvl > 0)                         // go one level down
                if (prev[lvl] == null) {         // if not the lowest
                      curr[lvl-1] = root[lvl-1]; // level, using a link
                      prev[lvl-1] = null;        // either from the root
                }
                else {                           // or from the predecessor;
                     curr[lvl-1] = prev[lvl].next[lvl-1];
                     prev[lvl-1] = prev[lvl];
                }
        }
        lvl = chooseLevel();                // generate randomly level
        newNode = new SkipListNode<T>(key,lvl+1); // for newNode;
        for (i = 0; i <= lvl; i++) {        // initialize next fields of
            newNode.next[i] = curr[i];      // newNode and reset to newNode
            if (prev[i] == null)            // either fields of the root
                 root[i] = newNode;         // or next fields of newNode's
            else prev[i].next[i] = newNode; // predecessors;
        }
    }
}