Balanced Search Tree

search tree data structure maintaining dynamic set of n elements using a tree of height order lgn .
Examples

  • AVL Tree
  • 2-3 Tree
  • 2-3-4 Tree
  • B Tree
  • Red-Black Trees
  • Skip lists
  • Treaps

    Red-Black Tree

    BST data structure with extra color field for each node satisfying.
    Red-Black properties
  1. Every Node is either red or black
  2. the root and the leaves(nil’s) are black
  3. Every red node has black parent
  4. All simple paths from a node x to a descended leaf of x have same number of black nodes . which means have the same black-height(x)

image.png
定理 ： Red-Black tree with n keys has height h <= 2lg(n+1)
证明：《算法导论》上有归纳法的详细证明
image.png

  • Merge red nodes into their black parents.
  • This process produce a tree in which each node has 2,3 or 4 children
  • the 2-3-4 tree has uniform depth h’ of leaves
  • We have Day 10 - 图3, since at most half the leaves on any path are red
  • The number of leaves in each tree is n+1Day 10 - 图4

Corollary . The queries Search, Min, Max, Successor, and Predecessor all run in O(lgn) time on a red-black tree with n nodes.

Modifying operations
The operations Insert and Delete cause modifications to the red-black tree:

  • the operation itself,
  • color changes,

  • restucturing the links of the tree via rotations

    Rotations

    image.png
    A rotation can be performed in O(1) time.

    Insertion into a red-black tree

    IDEA : Insert x in tree. Color x red. Only red-black property 3 might be violated. Move the violation up the tree by recoloring until it can be fixed with rotations and recolored.
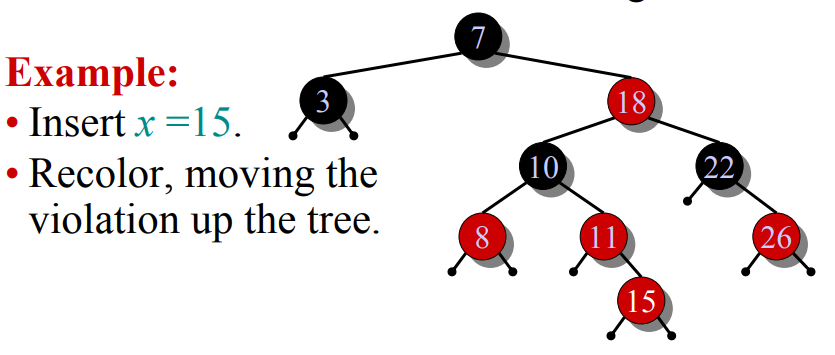
    image.png

    1. RB-INSERT(T,x)
    2.   Tree-INSERT(T,x)
    3. color[x]=red
    4. while x!=root[T] and color[p[x]]=RED
    5.     do if p[x]=left[p[p[x]]]
    6.       then y=right[p[p[x]]]
    7.         if color[y]=RED
    8.       then <Case 1>
    9.       else if x=right[p[x]]
    10.           then <case 2>
    11.       <Case 3>
    12.     else<"Then" clause with "left" and "right" swapped>
    13. color[root[T]]=black

    image.png
    image.png
    image.png
    Analysis

  • Go up the tree performing Case 1, with only recolors node.

  • If Case 2 or Case 3 occurs, perform 1 or 2 rotations, and terminate.

Running Time
O(lgn) with O(1) rotations.
RB-Delete: same asymptotic running time and number of rotations as RB-Insert(See textbook).