扩充的数据结构、动态有序统计和区间树

augmentation data structures 数据结构的扩充

Dynamic order statistics

新增的两个操作：

• OS-Select(i): returns i-th smallest item in dynamic set
• OS-Rank(i): returns rank of x in sorted order.

IDEA : Keep subtree size in node of r-b trees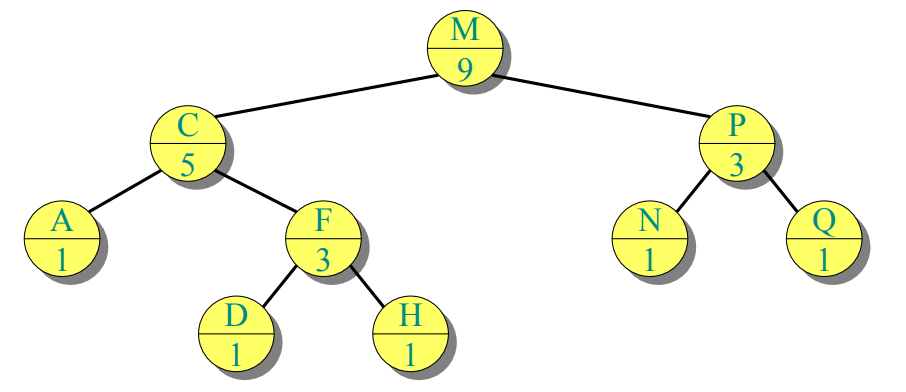

size[x] = size[left[x]]+size[right[x]]+1

OS-Select(i)

OS-Select(x,i) //i-th smallest in subtree rooted at x
    r = x.left.size + 1; //rank of x
  if i==r
      return x
  else if i<r
      return OS-Select(x.left,i)
  else
      return OS-Select(x.right,i-r)

OS-Rank(i)

OS-RANK(T,x)
    r = x.left.size + 1
  y = x
  while y!=T.root
      if y==y.p.right
        r = r + y.p.left.size + 1
    y = y.p
     return r

Analysis T(n)=O(lgn)
Q: Why not keep the ranks in nodes instead of subtree sizes?
A: It’s hard to maintain when t-b tree is motified.
Mutifying operations: Insert and Delete
Stratege : Update subtree sizes when inserting or deleting.
EX: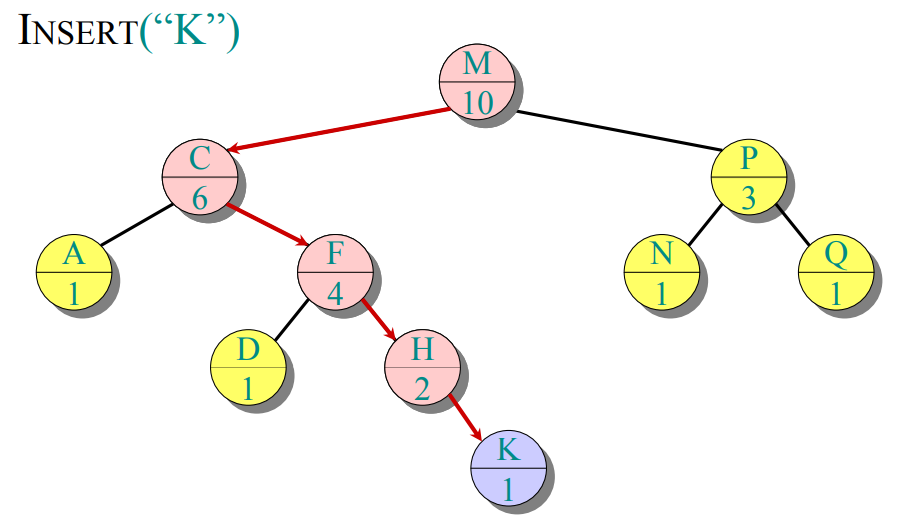

but also need to handle rebalancing

• r-b color changes: no effect to size
• rotation: look at children and fix up in O(1) time

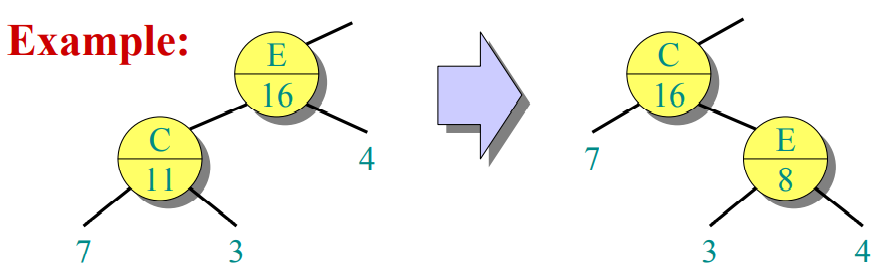
So, RB-Insert and RB-Delete still run in O(lgn) time

Data-structrue augmentation

Methodology : (e.g. order-statistics trees)

1. Choose an underlying data structrue.(red-black trees)
2. Determine additional information to be stored in the data structure.(subtree size)
3. Verify that this information can be maintained for modifying operations.(RBINSERT, RB-DELETE — don’t forget rotations)
4. Develop new dynamic-set operations that use the informations.(OS-Select and OS-Rank)

These steps are guidelines, not rigid rules

Example: Interval trees 区间树

IDEA ：maintain a set of intervals. e.g. time intervals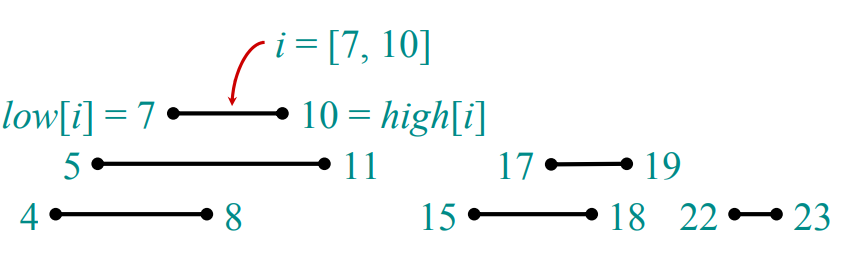

Query : For a given query interval i, find an interval in the set that overlaps i.

Methodology

1. Choose an underlying data structure.

(Red-Black Tree key on low(left) endpoint )

1. Determine additional information to be stored in the data structure.

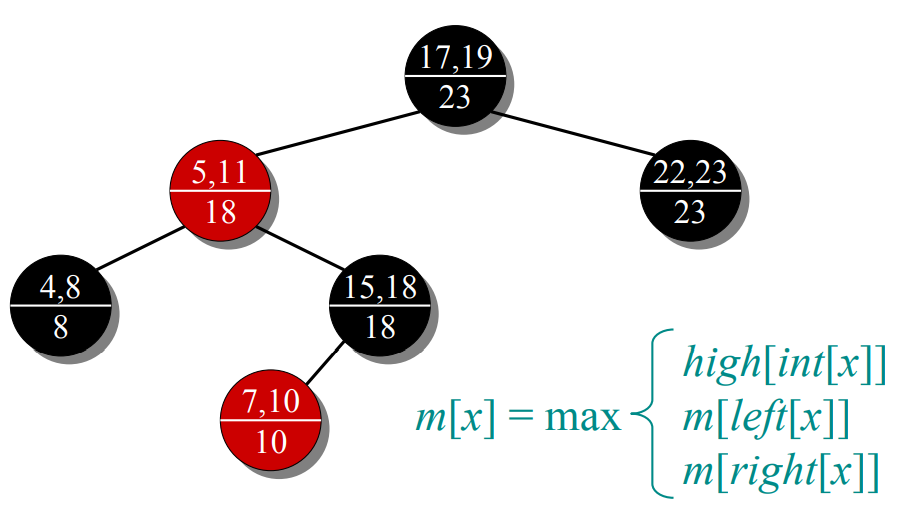
1. Modifying operations:
   Insert: fix m’s on way down .

   Rotations——Fixup = O(1) time per rotation:
   
   So, Total Insert Time = O(lgn) Delete similar

2. Develop new dynamic-set operations that use the information.

   INTERVAL-SEARCH(T,i)
    x = T.root
   while x!=nil and (low[i]>high[int[x]] or high[i]<low[int[x]]) // i does not overlaps x
      if x.left!=nil and x.left.m >= low[i]
        x=x.left
    else x = x.right
   return x
   

   List all overlaps: O(klgn) Output sensitive
   Correctness
   Theorem. Let L be the set of intervals in the left subtree of node x, and let R be the set of intervals in x’s right subtree.
   If the search goes right, then
   
   If the search goes left, then
   
   证明略