2-3树

2–3树是一种树型数据结构)，内部节点（存在子节点的节点）要么有2个孩子和1个数据元素，要么有3个孩子和2个数据元素，叶子节点没有孩子，并且有1个或2个数据元素。

定义

如果一个内部节点拥有一个数据元素、两个子节点，则此节点为2节点。
如果一个内部节点拥有两个数据元素、三个子节点，则此节点为3节点。
当且仅当以下叙述中有一条成立时，T为2–3树：

• T为空。即T不包含任何节点。
• 为拥有数据元素a的2节点。若T的左孩子为L、右孩子为R，则：L和R是等高的非空2–3树；a大于L中的所有数据元素；且a小于等于R中的所有数据元素。
• T为拥有数据元素a和b的3节点，其中a < b。若T的左孩子为L、中孩子为M、右孩子为R，则：L、M、和R是等高的非空2–3树；a大于L中的所有数据元素，并且小于等于M中的所有数据元素；b大于M中的所有数据元素，并且小于等于R中的所有数据元素。

  2-3树的查找

  与普通二叉搜索树相似。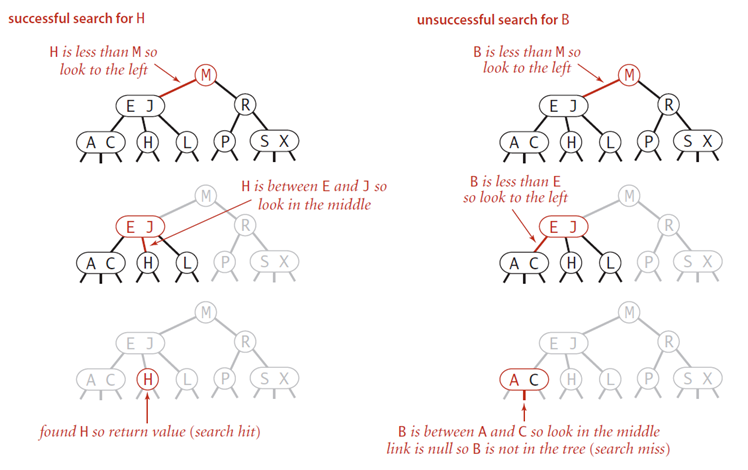
  

  2-3树的插入

  前面我们知道，2-3查找树分为2结点和3结点，so，插入就分为了2结点插入和3结点插入。
  2-结点插入: 向2-结点插入一个新的结点和向而插入插入一个结点很类似，但是我们并不是将结点“吊”在结点的末尾，因为这样就没办法保持树的平衡。我们可以将2-结点替换成3-结点即可，将其中的键插入这个3-结点即可。（相当于缓存了这个结点）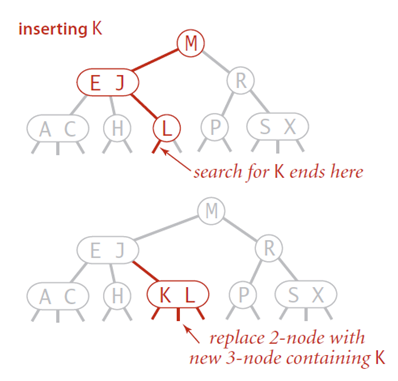
  
  3-结点插入： 3结点插入比较麻烦，它分为3种情况：

1. 向一棵只含有3-结点的树插入新键。

   假如2-3树只有一个3-结点，那么当我们插入一个新的结点的时候，我们先假设结点变成了4-结点，然后使得中间的结点为根结点，左边的结点为其左结点，右边的结点为其右结点，然后构成一棵2-3树，树的高度加1。
   

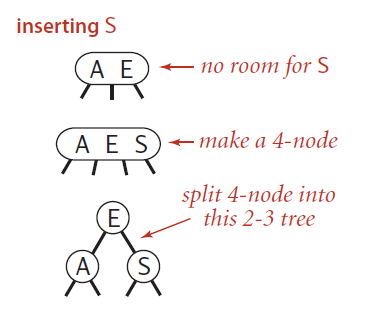
2. 向父结点为2-结点的3-结点中插入新键。

和上面的情况类似，我们将新的节点插入3-结点使之成为4-结点，然后将结点中的中间结点”升“到其父节点（2-结点）中的合适的位置，使其父节点成为一个3-节点，然后将左右节点分别挂在这个3-结点的恰当位置，树的高度不发生改变。
**

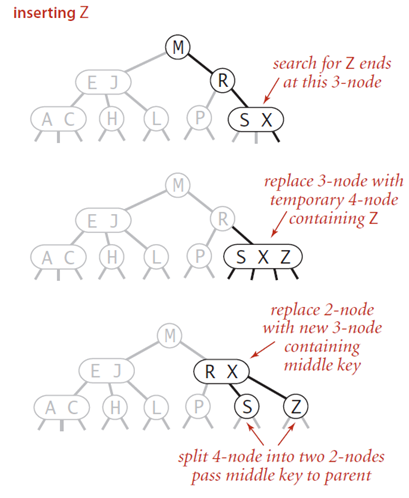
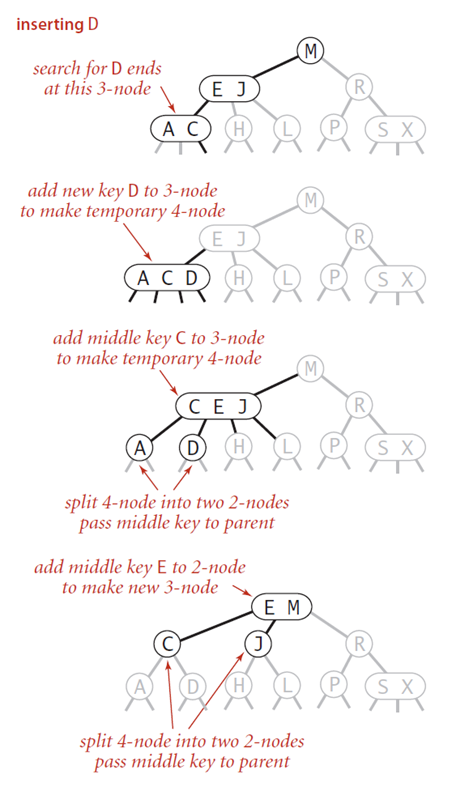
1. 向父节点为3-结点的3-结点中插入新键。

   这种情况有点类似递归：当我们的结点为3-结点的时候，我们插入新的结点会将中间的元素”升“父节点，然后父节点为4-结点，右将中间的结点”升“到其父结点的父结点，……如此进行递归操作，直到遇到的结点不再是3-结点。
   
   树的高度 ：