散列表

散列表是普通数组概念的推广，因为可以对数组进行直接寻址，故可以在O(1)的时间内访问数组的任意元素。

直接寻址法

当关键字的全域U比较小时，直接寻址是一种简单而有效的技术。假设某应用要用到一个动态集合，其中每个元素都有一个取自全域U={0,1,…,m-1}的关键字，此处m是一个很大的数。另，假设没有两个元素具有相同的关键字。
为表示动态集合，我们用一个数组（或称直接寻址表）T[0,…,m-1]，其中每个位置（或称槽）对应全域U中的一个关键字。对SEARCH、INSERT、DELETE等操作均只需O(1).

散列表

直接寻址技术存在一个明显的问题：如果域U很大，在一台典型计算机的可用内从容量限制下，要在机器中存储大小为|U|的一张表T就优点不切实际，甚至不可能。还有，实际要存储的关键字集合K相对于U来说可能很小，因而分配给T 的大部分空间都要浪费掉。
在直接寻址方式下， 具有关键字k的元素被存放在槽k中 。在散列方式下， 该元素处于h(k)中 。即利用散列函数h，根据关键字k计算出槽的位置。 函数h将关键字域U映射到散列表T[0,…,m-1]的槽位上 。
这样做有一个小问题： 两个关键字可能映射到同一个槽位上 ，我们称之为 碰撞 。

通过链接法来解决碰撞

在链接法中，把散列到同一槽的所有元素都放在一个链表中。槽j中有一个指针，它指向由所有散列到j的元素构成的链表的头。
采用链接法后散列表的性能怎么样呢？特别的，要查找一个具有给定关键字的元素需要多长时间？
给定一个能存放n个元素的、具有m个空槽位的散列表T，定义T的装载因子(Load factor)，即一个链表中平均存储的元素数。
Worst-Case：所有的n个关键字都散列到同一个槽内，Θ(n).
若假定任何元素散列到m个槽中的每一个可能性是相同的，且与其他元素已被散列到什么位置上是无关的，即 简单一致性假设
则在简单一致性假设下，对于用链接技术解决碰撞的散列表，平均情况下一次成功或不成功的查找需要

散列函数

在这一节里，讨论一些有关如何设计出好的散列函数的问题。

除法散列法

通过取k除以m的余数，来将关键字k映射到m个槽的某一个去。即，散列函数为 h(k) = k mod m
当应用除法散列时，应 注意m的选择 。可以选作m的值常常是 与2的整数幂不太接近的质数

乘法散列法

构造散列函数的乘法方法包含两个步骤：首先，用关键字k乘上常数A（0

全域散列

如果让某个和你作对的人来选择要散列的关键字，那么他会选择全部散列到同一个槽中的n个关键字，使得平均检索时间为Θ(n)。任何一个特定的散列函数都可能出现这种最坏情况形态：唯一有效的改进方法是 随机地选择散列函数 ，使之独立于要存储地关键字，这种方法称之为 全域散列 。

开放寻址法

开放寻址法（openning addressing）中，所有的元素都存放在散列表里。亦即，每个表项或包含动态集合的一个元素，或包含nil。当查找一个元素时，要检查所有的表项，直到找到所需元素，或最终发现该元素不在表中。
线性勘查
当冲突发生时，使用某些探测技术在散列表中形成一个探测序列，沿此序列逐个单元查找，直到找到给定的关键字、或者碰到一个开放地 址（即该地址单元为空、空桶）为止。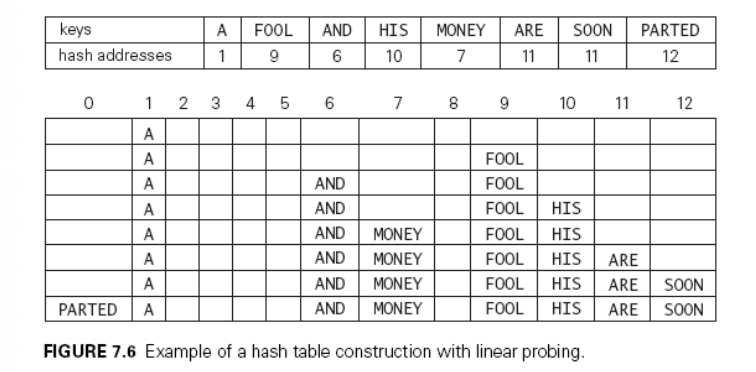

双重散列
双重散列是用于开放寻址的最好方法之一，因为它所产生的排列具有随机选择的排列的许多特性。它采用如下形式的散列函数：

对开放寻址散列的分析

Assumption : 一致散列法 ：在这种理想的方法中，用于插入或查找每一个关键字k的探索序列为<0,1,...,m-1>的任一中排列的可能性是相同的。
则在该假设下： 给定一个装载因子a=n/m<1的开放寻址散列表，在一次不成功的查找中，期望的勘察天数至多为1/(1-a)