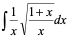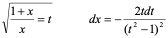第四章不定积分
教学目的与要求
1.理解原函数概念、不定积分和定积分的概念。
2. 掌握不定积分的基本公式,掌握不定积分和定积分的性质及定积分中值定理,掌握换元积分法与分部积分法。
3. 求有理函数、三角函数有理式和简单无理函数的积分。
在第二章中,我们讨论了怎样求一个函数的导函数问题,本章将讨论它的反问题,即要求一个导函数的原函数,也就是求一个可导函数,使它的导函数等于已知函数。这是积分学的基本问题之一 。
4.1 不定积分的概念与性质
一 原函数与不定积分的概念
定义1 如果在区间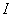 上,可导函数
上,可导函数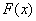 的导函数为
的导函数为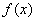 ,即对任一
,即对任一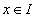 ,都有
,都有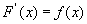 或
或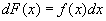 ,
,
那末函数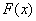 就称为
就称为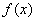 (或
(或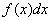 )在区间
)在区间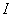 上的原函数。
上的原函数。
例如,x^2是2x的原函数,lnx是1/x的原函数因,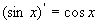 ,故
,故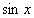 是
是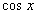 的原函数。
的原函数。
注:1由此定义上问题是:已知f(x),如何去求原函数
2.那一个函数具备何种条件,才能保证它的原函数一定存在呢?若存在是否唯一定理1:若f(x)在I上连续,则f(x)在I上一定有原函数。
注意:并不是任意在I上有定义的函数都有原函数,反例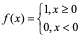
定理2:设f(x)在区间I上有原函数,且F(x)是其中一个原函数,则
1. f(x)的任意两个原函数相差一个常数
2. F(x)+C也是f(x)的原函数
定义2 在区间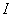 上,函数
上,函数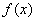 的带有任意常数项的原函数称为
的带有任意常数项的原函数称为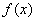 (或
(或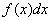 )在区间
)在区间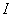 上的不定积分,记作
上的不定积分,记作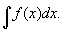 。
。
其中记号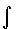 称为积分号,
称为积分号,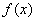 称为被积函数,
称为被积函数,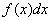 称为被积表达式,
称为被积表达式,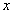 称为积分变量。
称为积分变量。
由此定义及前面的说明可知,如果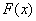 是
是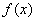 在区间
在区间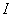 上的一个原函数,那么
上的一个原函数,那么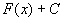 就是
就是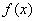 的不定积分,即
的不定积分,即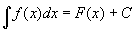 。
。
因而不定积分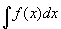 可以表示
可以表示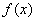 的任意一个原函数。
的任意一个原函数。
第一,如果有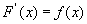 ,那么,对任意常数C,显然也有
,那么,对任意常数C,显然也有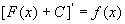 ,即如果
,即如果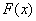 是
是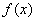 的原函数,那
的原函数,那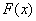
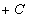 也是
也是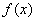 的原函数。
的原函数。
第二,当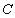 为任意常数时,表达式
为任意常数时,表达式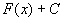
就可以表示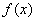 的任意一个原函数。也就是说,
的任意一个原函数。也就是说,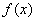 的全体原函数所组成的集合,就是函数族
的全体原函数所组成的集合,就是函数族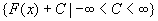 。
。
例 1 求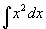 .
.
解 由于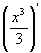 =
=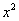 ,所以
,所以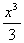 是
是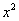 的一个原函数。因此
的一个原函数。因此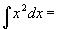
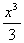
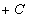 .
.
例 2 求 .
.
解 当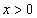 时,由于
时,由于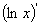 =
= ,所以
,所以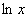 是
是 在
在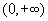 内的一个原函数。因此,在
内的一个原函数。因此,在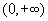 内,
内,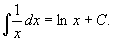
当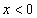 时,由于
时,由于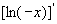 =
=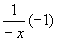 =
= ,由上同理,在
,由上同理,在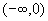 内,
内,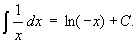
将结果合并起来,可写作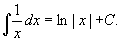
例3、 已知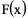 是
是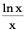 的一个原函数,
的一个原函数,
求: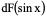
解:
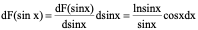
例4、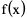 的导函数是
的导函数是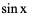 ,则
,则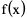 的原函数
的原函数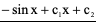 ,(
,(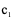 、
、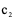 为任意常数)
为任意常数)
例5、在下列等式中,正确的结果是 C
A、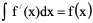 B、
B、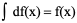
C、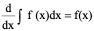 D、
D、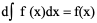
二基本积分表
由于积分是微分的逆运算,因此可以有微分基本表导出积分表。见课本积分表。
三不定积分的性质
根据不定积分的定义,可以推得它的如下两个性质:
性质1 函数的和的不定积分等于各个函数的不定积分的和,即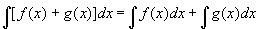 .
.
注意:差的积分等于积分的差
性质2 求不定积分时,被积函数中不为零的常数因子可以提到积分号外面来,即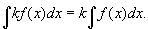 (
(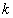 是常数,
是常数,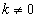 ).
).
例 1 求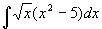 .
.
解 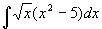 =
=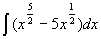
=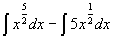
=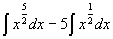
=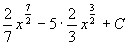
=
例2.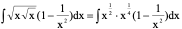
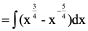
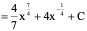
例3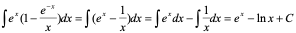
例4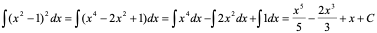 **4.2 两类换元法及举例
**4.2 两类换元法及举例
利用基本积分表与积分的性质,所能计算的不定积分是非常有限的.因此,有必要进一步来研究不定积分的求法.把复合函数的微分法反过来求不定积分,利用中间变量的代换,得到复合函数的积分法,称为换元积分法,简称换元法.
换元法通常分成两类.
一.
设f(u)具有原函数F(u),即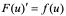 和
和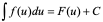 令u =φ(x),其中φ(x)是可导的,则F(u)=F(φ(x))显然是复合函数,又由于:
令u =φ(x),其中φ(x)是可导的,则F(u)=F(φ(x))显然是复合函数,又由于: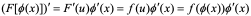
这说明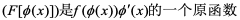 ,则
,则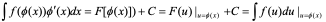
定理1 设f(u)具有原函数F(u), u =φ(x)可导, 则有换元公式: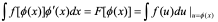
注意:
1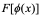 不是
不是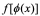 的原函数!
的原函数!
2 F(u)是f(u)的原函数是针对积分变量u而言的,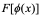 是
是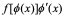 的原函数是针对积分变量x而言的。
的原函数是针对积分变量x而言的。
3运用第一类积分换元法关键在于设法将被积函数凑成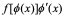 的形式,在令
的形式,在令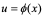 变成不定积分
变成不定积分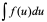 进行计算,最后用
进行计算,最后用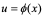 进行回代。
进行回代。
4在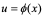 下,
下, ,
,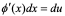
例1 求∫2cos2xdx.
解 作变换u=2x,便有
∫2cos2xdx =∫cos2x·2dx =∫cos2x·(2x)’ dx =∫cos u du = sin u+C,
再以u=2x代入,即得
∫2cos2xdx =sin 2x+C.
例2 求∫tan x dx.
解 ∫tan x dx =∫sin x /cos x dx.
因为 -sin x dx = d cos x,所以如果设u=cos x,那么du=-sin xdx,即 -du=sin xdx,因此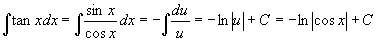 .
.
类似地可得∫cot x dx =ln|sin x|+C.
在对变量代换比较熟练以后,就不一定写出中间变量u.
例3 求∫ch(x/a) dx.
解 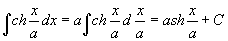 .
.
例4 求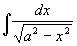 (a>0).
(a>0).
解 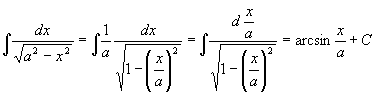 .
.
下面的一些求积分的例子,它们的被积函数中含有三角函数,在计算这种积分的过程中,往往要用到一些三角恒等式.
例5 求∫sin x dx.
解 ∫sinx dx =∫sinx sinx dx=-∫(1-cosx)d(cosx)
=-∫d(cosx)+∫cosxd(cosx)
=-cosx+(1/3)cosx+C.
例6 求∫cos x dx.
解 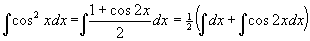
 .
.
附加:
1、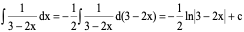
2、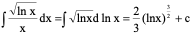
3、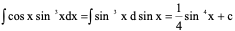
4、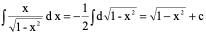
5、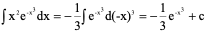
6、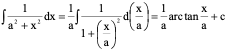
利用定理1来求不定积分,一般却比利用复合函数的求导法则求函数的导数要来的困难,因为其中需要一定的技巧,而且如何适当的选择变量代换u=φ(x)没有一般途径可循,因此要掌握换元法,除了熟悉一些典型的例子外,还要做较多的练习才行.
二 第二类换元法
第二类换元法从 形式上看与第一类换元法恰好相反,它是将不定积分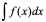 通过
通过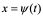 转换成
转换成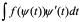 来计算,但有几点需要说明。1
来计算,但有几点需要说明。1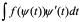 要存在,2尽量寻找这样的
要存在,2尽量寻找这样的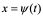 使
使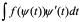 容易求出,3。求出后要用
容易求出,3。求出后要用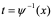 将积分变量换回到x,因此这里还要求
将积分变量换回到x,因此这里还要求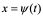 的反函数存在。
的反函数存在。
定理2 设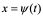 是单调的、可导的函数, 并且
是单调的、可导的函数, 并且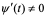 . 又设
. 又设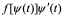 具有原函数
具有原函数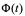 ,,则f(x)具有原函数
,,则f(x)具有原函数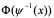 则有换元公式:
则有换元公式: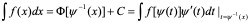
其中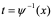 是
是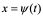 的反函数.
的反函数.
证明: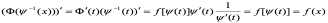 所以
所以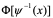 是f(x)的原函数,从而
是f(x)的原函数,从而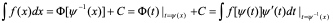
例1 求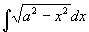 (a>0)
(a>0)
解 求这个积分的困难在于有根式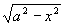 ,但我们可以利用三角公式sint+cost=1来化去根式.
,但我们可以利用三角公式sint+cost=1来化去根式.
设x=asint,-π/2<_t_<π/2,那么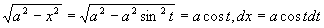,于是根式化为了三角式,所求积分化为.
利用例6的结果得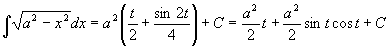 .
.
由于x=asint,-π/2<_t_<π/2,所以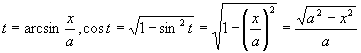 ,
,
于是所求积分为 .
.
具体解题时要分析被积函数的具体情况,选取尽可能简捷的代换.
注意 检验积分结果是否正确,只要对结果求导,看它的导数是否等于被积函数,相等时结果是正确的,否则结果是错误的。
常用变量代换
(1)被积函数中含有二次根式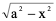 ,令
,令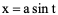
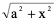 ,令
,令
 ,令
,令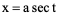
如是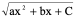 配方
配方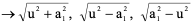
| 1 | |
|---|---|
| | —- |
例2、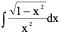 令
令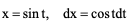
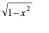
| x | |
|---|---|
| | —- |
| t | |
|---|---|
| | —- |
解:原式 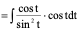
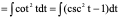
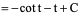
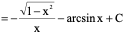
例3、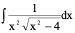 二种解法
二种解法
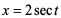
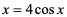
(2)被积函数中含一般根式
例4、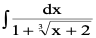
解:令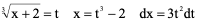
原式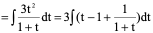
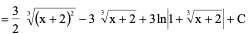
例5、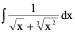 令
令 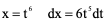
原式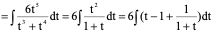

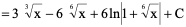
例6、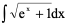
解:令 
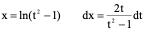
原式 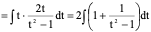
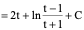
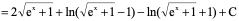
4.3分部积分法
这是一个新的积分方法,设u(x),v(x)具有连续导数,则有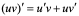 ,即
,即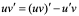 ,两边同时积分则有,
,两边同时积分则有,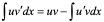 即
即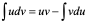 ,上式就是分布积分公式。
,上式就是分布积分公式。
注意:使用分部积分的关键是如何选取u和v
例1、
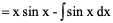
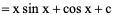
例2、
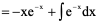
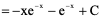
例3、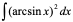
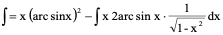
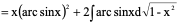
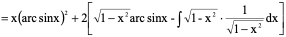
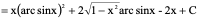
例4、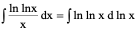
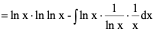
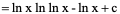
例5、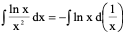
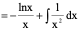
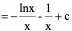
例6、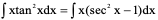
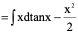
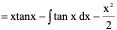
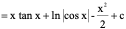
例7、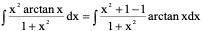
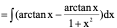
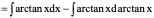
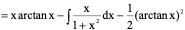
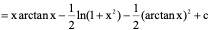
例8、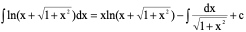
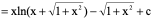
例9、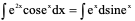
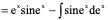
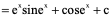
例10、
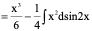
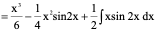
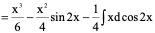
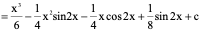
例11、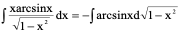
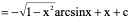
注意:
1一般而言分部积分法和换元法同时使用会有更好的效果。
2分部积分常适用于下列积分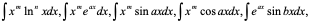
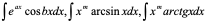 等等。
等等。
4.4几种特殊类型的函数积分举例
一有理函数的积分举例
有理函数是指形如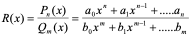 ,其中 ,m,n为正整数或者0,
,其中 ,m,n为正整数或者0,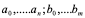 都是常数,且
都是常数,且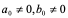 ,当n<m是真分式,当
,当n<m是真分式,当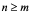 时是假分式,但总可以通过多项式除法写成一个多项式与一个真分式的和,因此问题就集中在解决真分式的积分问题。
时是假分式,但总可以通过多项式除法写成一个多项式与一个真分式的和,因此问题就集中在解决真分式的积分问题。
定理1:任何实多项式都可以分解成为一次因式与二次因式的乘积。
定理2:有理函数的分解
部分分式: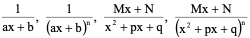
其中: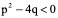 上述常数用待定系数法可以确定。
上述常数用待定系数法可以确定。
方法:分式→真分式→部分分式
例: 1) 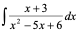
解: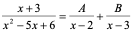 用待定系数法:A=-5,B=6
用待定系数法:A=-5,B=6
则: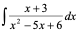 =
=
2)
解: 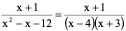
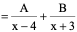

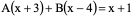
令 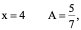
令 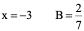
∴ 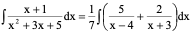
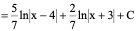
3) 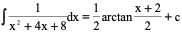
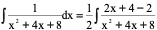
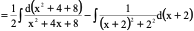
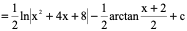
备用习题:
4) 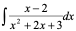
5) 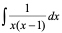
6) 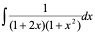
二 三角有理式积分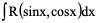
三角函数的有理式是指三角函数经过有限次四则运算所构成的函数求这类函数的积分是可以通过如下变换计算:
令 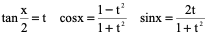
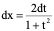
1、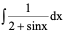
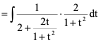
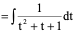
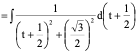
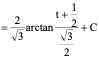

2、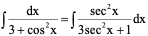
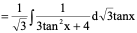
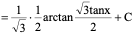
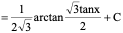
3 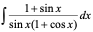
解: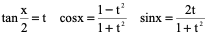
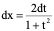 则:
则: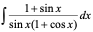 =
=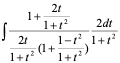

=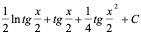
注意:一般而言,万能公式具有通用性,但不一定是最简单的。
三.简单无理函数积分举例
1) 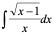
解:令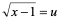
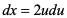
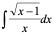 =
=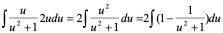
=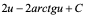 =
=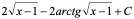
2) 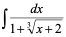
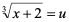
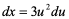
解: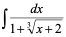 =
=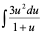 =
=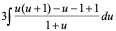
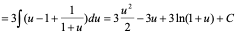
=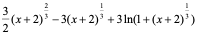 +C
+C
备用题:
3) 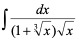
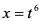
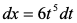
4)