本文所有代码运行环境均为Visual Studio Code
- 数据(data):对客观事物的符号表示,所有能被输入到计算机中,且能被计算机处理的符号的集合。是计算机操作的对象的总称。是计算机处理的信息的某种特定的符号表示形式。
- 数据元素: 是数据(集合)中的一个“个体”,是数据结构中讨论的基本单位。
数据项:是数据结构中讨论的最小单位
数据元素可以是数据项的集合
数据结构:是相互之间存在一种或多种特定关系的数据元素的集合;带结构的数据元素的集合,或者说,数据结构是相互之间存在着某种逻辑关系的数据元素的集合。
1.1 数据的逻辑结构:数据对象中数据元素之间的相互关系
- 数据的逻辑结构从逻辑关系上描述数据,与数据的存储无关;
- 数据的逻辑结构可以看作是从具体问题抽象出来的数据模型;
- 数据的逻辑结构与数据元素本身的形式、内容无关;
- 数据的逻辑结构与数据元素的相对位置无关。
- 数据的逻辑结构分类
- 线性结构
- 线性表
- 非线性结构
- 树
- 图(或网络)
- 线性结构
- 集合结构:集合结构中的数据元素除了同属于一个集合外,他们之间没有其他关系
- 线性结构:线性结构中的数据元素之间是一对一的关系
- 树形结构:树形结构中的数据元素之间存在一对多的层次关系
- 图形结构:图形结构的数据元素是多对多的关系
1.2 数据的物理(存储)结构:数据的逻辑结构在计算机中的存储形式
- 数据的存储结构是逻辑结构用计算机语言的实现;
- 数据的存储结构依赖于计算机语言。
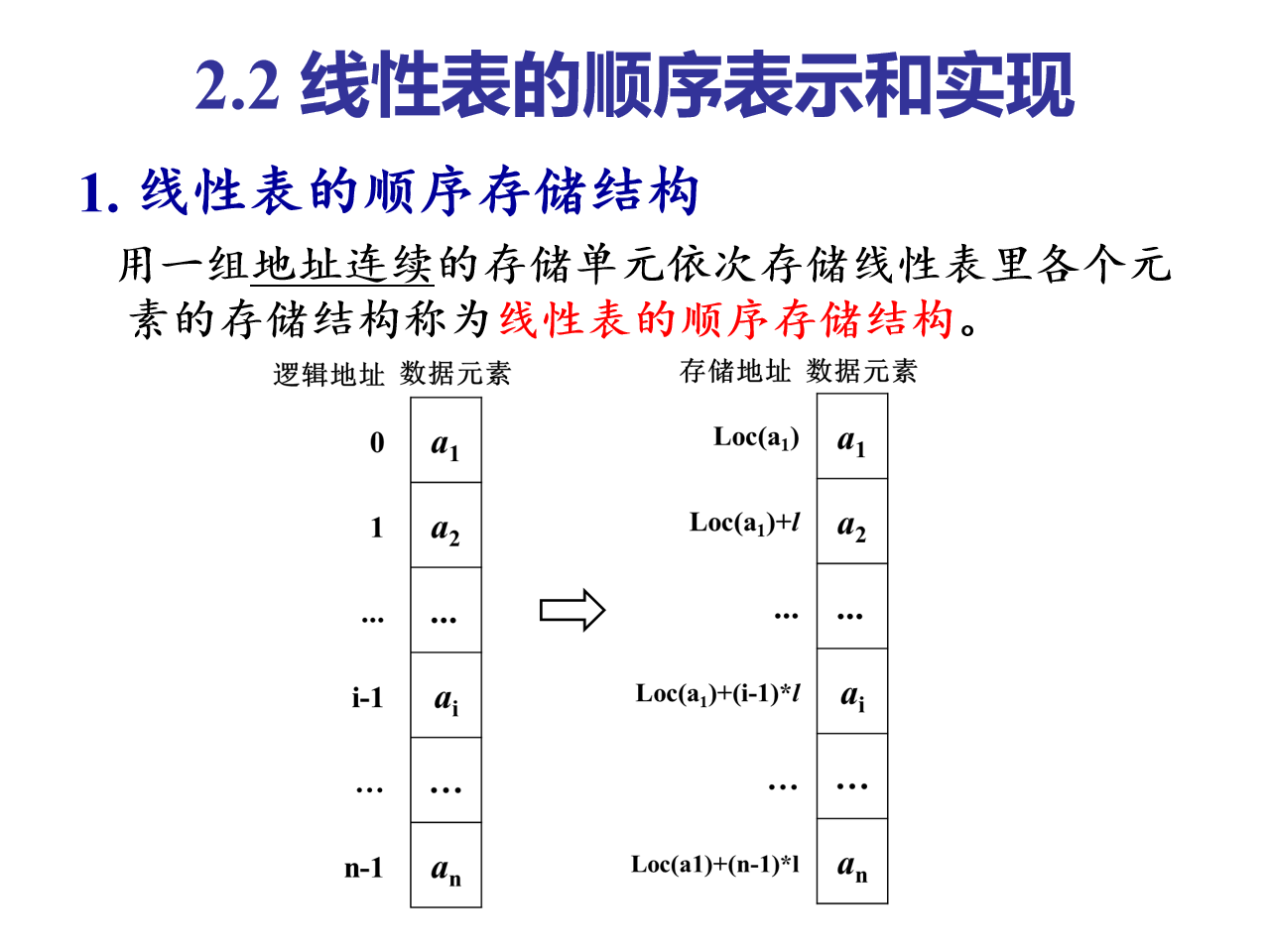
- 顺序存储结构:是把数据元素存放在地址连续的存储单元里,其数据之间的逻辑关系和物理关系是一致的
- 链接存储结构:把数据元素存放在任意的存储单元里,这里的存储单元可以是连续的,也可以是不连续的
- 索引存储结构
- 散列存储结构
1.3 抽象数据类型及面向对象概念
数据类型:是指一组性质相同的值的集合及定义在此集合上的一些操作的总称
定义:一组性质相同的值的集合, 以及定义于这个值集合上的一组操作的总称.
- 构造数据类型由基本数据类型或构造数据类型组成。
- 构造数据类型由不同成分类型构成。
- 基本数据类型可以看作是计算机中已实现的数据结构。
- 数据类型就是数据结构,不过它是从编程者的角度来使用的。
- 数据类型是模板,必须定义属于某种数据类型的变量,才能参加运算。
1.4 算法,就是有穷规则的集合,其中的规则规定了解决某特定类型问题的运算序列
算法:算法是解决特定问题求解步骤的描述,在计算机中表现为指令的有限序列,并且每条指令表示一个或多个操作。
算法的特性
- 有穷性:一个算法在执行有限步之后必须结束。
- 确定性:算法的每一步骤必须确切定义。执行者可根据该算法的每一步要求进行操作,并最终得出正确的结果(即无歧义) 。
- 可行性:算法中所有的运算都可以精确地实现。
- 输入:算法有零个或多个输入,即在算法开始之前,对算法给定的初始量。
- 输出:算法有一个或多个输出,即与输入有某个特定关系的量,简单地说就是算法的最终结果。
算法的性能标准
- 正确性
- 可使用性
- 可读性
- 效率高
- 健壮性
算法效率的度量方法
- 事后统计方法:这种方法主要是通过设计好的测试程序和数据,利用计算机计时器对不同算法编制的程序的运行时间的比较,从而确定算法效率的高低。
- 事前分析估计方法:在计算机程序编制前,根据统计方法进行估算。
函数的渐近增长
- 函数的渐近增长:给定两个函数
和
,如果存在一个整数
,使得对于所有
,
总是大于
,那么我们说
的增长渐近快于
。(一般可以忽略常数)
- 判断一个算法的效率时,函数中的常数和其他次要项常常可以忽略,而更应该关注主项(最高阶项)的阶数。
1.4.1 算法时间复杂度
- 在进行算法分析时,语句总的执行次数
是关于问题规模
的函数,进行分析
随
的变化情况并确定
的数量级。算法的时间复杂度,也就是算法的时间度量,记作
。它表示随文题规模
的增大,算法执行时间的增长率和
的增长率相同,称作算法的渐近时间复杂度,简称为时间复杂度。其中
是问题规模
的某个函数。
- 这样用大写
来体现算法时间复杂度的技法,我们称之为大
记法。
- 推导大
阶
- 用常数1取代运行时间中的加法常数
- 在修改后的运行函数中,只保留最高阶项。
- 如果最高阶项存在且其系数不是1,则去除与这个项相乘的系数。得到的结果就是大
阶。
- 常数阶
- 线性阶
- 对数阶
- 平方阶
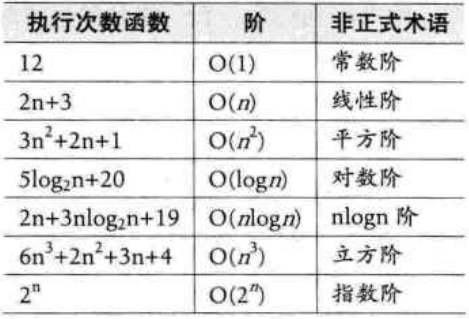 常用的时间复杂度所耗费的时间从小到大依次是:
常用的时间复杂度所耗费的时间从小到大依次是:
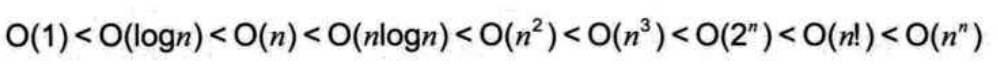
1.4.2 算法空间复杂度
- 算法的空间复杂度通过计算算法所需的存储空间实现,算法空间复杂度的计算式记作:
,其中,
为问题的规模,
为语句关于
所占存储空间的函数。
2. 第二章 线性表
线性表:零个或多个数据元素的有限序列。
线性结构的基本特征为:
- 集合中必存在唯一的一个“第一元素”;
- 集合中必存在唯一的一个 “最后元素” ;
- 除最后元素在外,均有 唯一的后继;
- 除第一元素之外,均有 唯一的前驱。
2.1 抽象数据类型线性表的定义如下
ADT List{数据对象:D={a_i|a_i属于ElenSet,i=1,2,...,n}数据关系:R1={<a_{i-1},a_i>|a_i属于D,i=1,2,...,n}基本操作:InitList(&L)/*初始化操作*/操作结果:构造一个空的线性表L。DestroyList(&L)/*结构销毁操作*/初始条件:线性表L已存在。操作结果:销毁线性表L。ClearList(&L)/*重置为空表*/初始条件:线性表L已存在。操作结果:将L重置为空表。ListEmpty(L)/*线性表判空*/初始条件:线性表L已存在。操作结果:若L为空表,则返回TRUE,否则返回FALSE。ListLength(L)/*求线性表的长度*/初始条件:线性表L已存在。操作结果:返回L中的元素个数。GetElem(L,i,&e)/*求线性表中某个数据元素*/初始条件:线性表L已存在,1<=i<=ListLength(L)。操作结果:用e返回L中第i个数据元素的值。LocateElem( L, e, compare( ))/*定位函数*/初始条件:线性表L已存在,e为给定值,compare( )是元素判定函数。操作结果:返回L中第1个与e满足关系compare( )的元素的位序。若这样的元素不存在,则返回值为0。PriorElem( L, cur_e, &pre_e )/*求数据元素的前驱*/初始条件:线性表L已存在。操作结果:若cur_e是L的元素,但不是第一个,则用pre_e 返回它的前驱,否则操作失败,pre_e无定义。NextElem( L, cur_e, &next_e )/*求数据元素的后继*/初始条件:线性表L已存在。操作结果:若cur_e是L的元素,但不是最后一个,则用next_e返回它的后继,否则操作失败,next_e无定义。ListInsert( &L, i, e )/*插入数据元素*/初始条件:线性表L已存在,且 1≤i≤LengthList(L)+1 。操作结果:在L的第i个元素之前插入新的元素e,L的长度增1。ListDelete(&L, i, &e)/*删除数据元素*/初始条件:线性表L已存在且非空,1≤i≤LengthList(L) 。操作结果:删除L的第i个元素,并用e返回其值,L的长度减1。PutElem( &L, i, &e )初始条件:线性表L已存在,且 1≤i≤LengthList(L) 。操作结果:L中第i个元素赋值同e的值。ListTraverse(L, visit( ))/*遍历线性表*/初始条件:线性表L已存在,Visit() 为某个访问函数。操作结果:依次对L的每个元素调用函数visit( )。一旦visit( )失败,则操作失败。}
2.2 线性表顺序存储结构(代码实例)
#include "stdio.h"#include "stdlib.h"#include "math.h"#include "time.h"#define OK 1#define ERROR 0#define TRUE 1#define FALSE 0#define MAXSIZE 20 /* 存储空间初始分配量 */typedef int ElemType; /* ElemType类型根据实际情况而定,这里假设为int */typedef struct{ElemType data[MAXSIZE]; /* 数组,存储数据元素 */int length; /* 线性表当前长度 */}SqList;typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */Status visit(ElemType c){printf("%d ",c);return OK;}/* 初始化顺序线性表 */Status InitList(SqList *L){L->length=0;return OK;}/* 初始条件:顺序线性表L已存在。操作结果:若L为空表,则返回TRUE,否则返回FALSE */Status ListEmpty(SqList L){if(L.length==0)return TRUE;elsereturn FALSE;}/* 初始条件:顺序线性表L已存在。操作结果:将L重置为空表 */Status ClearList(SqList *L){L->length=0;return OK;}/* 初始条件:顺序线性表L已存在。操作结果:返回L中数据元素个数 */int ListLength(SqList L){return L.length;}/* 初始条件:顺序线性表L已存在,1≤i≤ListLength(L) *//* 操作结果:用e返回L中第i个数据元素的值,注意i是指位置,第1个位置的数组是从0开始 */Status GetElem(SqList L,int i,ElemType *e){if(L.length==0 || i<1 || i>L.length)return ERROR;*e=L.data[i-1];return OK;}/* 初始条件:顺序线性表L已存在 *//* 操作结果:返回L中第1个与e满足关系的数据元素的位序。 *//* 若这样的数据元素不存在,则返回值为0 */int LocateElem(SqList L,ElemType e){int i;if (L.length==0)return 0;for(i=0;i<L.length;i++){if (L.data[i]==e)break;}if(i>=L.length)return 0;return i+1;}/* 初始条件:顺序线性表L已存在,1≤i≤ListLength(L), *//* 操作结果:在L中第i个位置之前插入新的数据元素e,L的长度加1 */Status ListInsert(SqList *L,int i,ElemType e){int k;if (L->length==MAXSIZE) /* 顺序线性表已经满 */return ERROR;if (i<1 || i>L->length+1)/* 当i比第一位置小或者比最后一位置后一位置还要大时 */return ERROR;if (i<=L->length) /* 若插入数据位置不在表尾 */{for(k=L->length-1;k>=i-1;k--) /* 将要插入位置之后的数据元素向后移动一位 */L->data[k+1]=L->data[k];}L->data[i-1]=e; /* 将新元素插入 */L->length++;return OK;}/* 初始条件:顺序线性表L已存在,1≤i≤ListLength(L) *//* 操作结果:删除L的第i个数据元素,并用e返回其值,L的长度减1 */Status ListDelete(SqList *L,int i,ElemType *e){int k;if (L->length==0) /* 线性表为空 */return ERROR;if (i<1 || i>L->length) /* 删除位置不正确 */return ERROR;*e=L->data[i-1];if (i<L->length) /* 如果删除不是最后位置 */{for(k=i;k<L->length;k++)/* 将删除位置后继元素前移 */L->data[k-1]=L->data[k];}L->length--;return OK;}/* 初始条件:顺序线性表L已存在 *//* 操作结果:依次对L的每个数据元素输出 */Status ListTraverse(SqList L){int i;for(i=0;i<L.length;i++)visit(L.data[i]);printf("\n");return OK;}/*将所有的在线性表Lb中但不在La中的数据元素插入到La中*/void unionL(SqList *La,SqList Lb){int La_len,Lb_len,i;ElemType e; /*声明与La和Lb相同的数据元素e*/La_len=ListLength(*La); /*求线性表的长度 */Lb_len=ListLength(Lb);for (i=1;i<=Lb_len;i++){GetElem(Lb,i,&e); /*取Lb中第i个数据元素赋给e*/if (!LocateElem(*La,e)) /*La中不存在和e相同数据元素*/ListInsert(La,++La_len,e); /*插入*/}}int main(){SqList L;SqList Lb;ElemType e;Status i;int j,k;i=InitList(&L);printf("初始化L后:L.length=%d\n",L.length);for(j=1;j<=5;j++)i=ListInsert(&L,1,j);printf("在L的表头依次插入1~5后:L.data=");ListTraverse(L);printf("L.length=%d \n",L.length);i=ListEmpty(L);printf("L是否空:i=%d(1:是 0:否)\n",i);i=ClearList(&L);printf("清空L后:L.length=%d\n",L.length);i=ListEmpty(L);printf("L是否空:i=%d(1:是 0:否)\n",i);for(j=1;j<=10;j++)ListInsert(&L,j,j);printf("在L的表尾依次插入1~10后:L.data=");ListTraverse(L);printf("L.length=%d \n",L.length);ListInsert(&L,1,0);printf("在L的表头插入0后:L.data=");ListTraverse(L);printf("L.length=%d \n",L.length);GetElem(L,5,&e);printf("第5个元素的值为:%d\n",e);for(j=3;j<=4;j++){k=LocateElem(L,j);if(k)printf("第%d个元素的值为%d\n",k,j);elseprintf("没有值为%d的元素\n",j);}k=ListLength(L); /* k为表长 */for(j=k+1;j>=k;j--){i=ListDelete(&L,j,&e); /* 删除第j个数据 */if(i==ERROR)printf("删除第%d个数据失败\n",j);elseprintf("删除第%d个的元素值为:%d\n",j,e);}printf("依次输出L的元素:");ListTraverse(L);j=5;ListDelete(&L,j,&e); /* 删除第5个数据 */printf("删除第%d个的元素值为:%d\n",j,e);printf("依次输出L的元素:");ListTraverse(L);//构造一个有10个数的Lbi=InitList(&Lb);for(j=6;j<=15;j++)i=ListInsert(&Lb,1,j);unionL(&L,Lb);printf("依次输出合并了Lb的L的元素:");ListTraverse(L);return 0;}
输出
初始化L后:L.length=0在L的表头依次插入1~5后:L.data=5 4 3 2 1L.length=5L是否空:i=0(1:是 0:否)清空L后:L.length=0L是否空:i=1(1:是 0:否)在L的表尾依次插入1~10后:L.data=1 2 3 4 5 6 7 8 9 10L.length=10在L的表头插入0后:L.data=0 1 2 3 4 5 6 7 8 9 10L.length=11第5个元素的值为:4第4个元素的值为3第5个元素的值为4删除第12个数据失败删除第11个的元素值为:10依次输出L的元素:0 1 2 3 4 5 6 7 8 9删除第5个的元素值为:4依次输出L的元素:0 1 2 3 5 6 7 8 9依次输出合并了Lb的L的元素:0 1 2 3 5 6 7 8 9 15 14 13 12 11 10
2.3 线性表类型的实现——顺序存储结构
线性表的顺序存储结构,指的是用一段地址连续的存储单位依次存储线性表的数据元素。
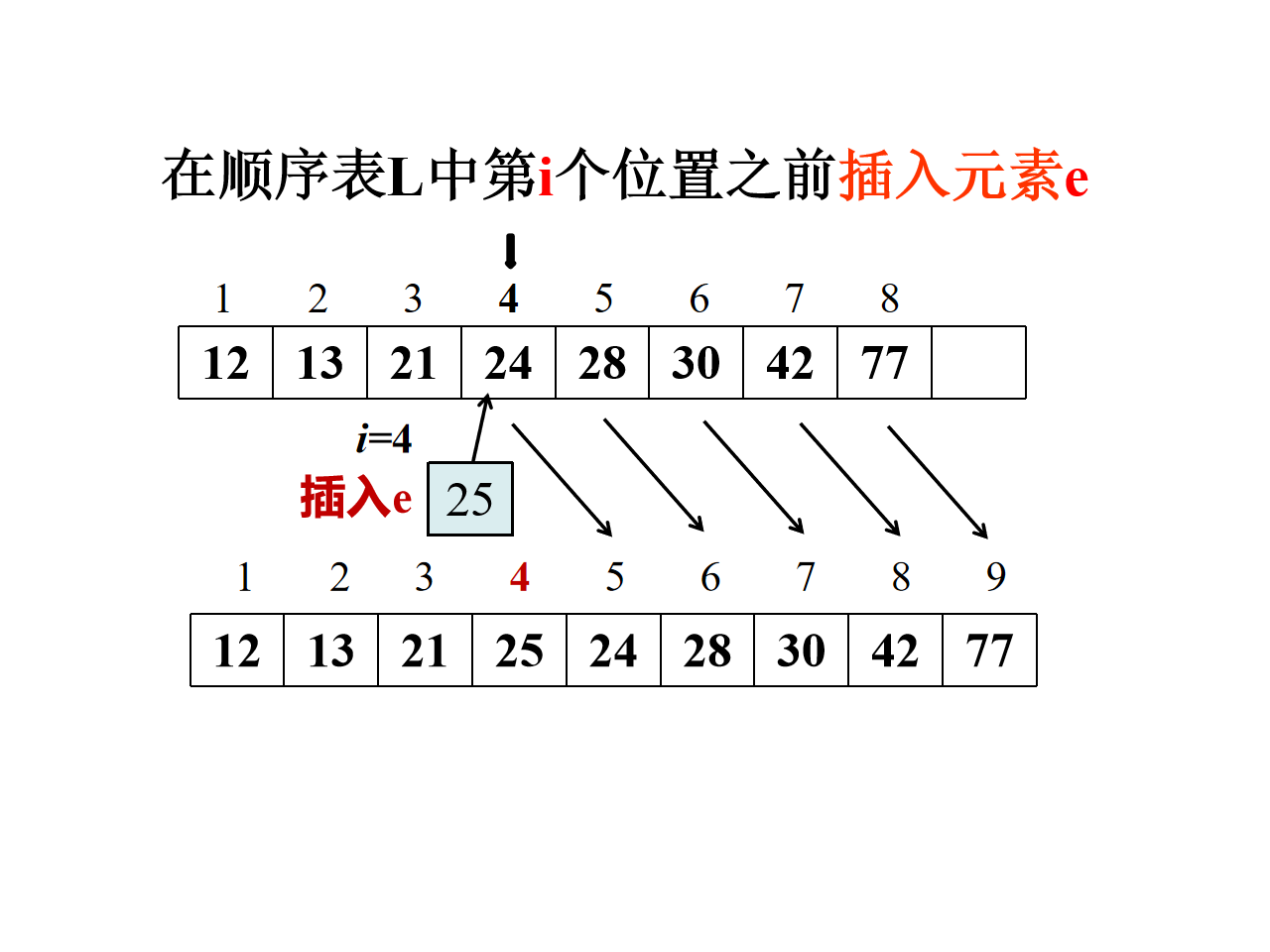
2.3.1 顺序表元素插入
Status ListInsert(SqList *L,int i,ElemType e){int k;if (L->length==MAXSIZE)return ERROR;if (i<1 || i>L->length+1)return ERROR;if (i<=L->length){for(k=L->length-1;k>=i-1;k--)L->data[k+1]=L->data[k];}L->data[i-1]=e;L->length++;return OK;}
2.3.2 顺序表元素删除
Status ListDelete(SqList *L,int i,ElemType *e){int k;if (L->length==0)return ERROR;if (i<1 || i>L->length)return ERROR;*e=L->data[i-1];if (i<L->length){for(k=i;k<L->length;k++)L->data[k-1]=L->data[k];}L->length--;return OK;}
2.4 线性表链式存储结构(代码实例)
#include "stdio.h"#include "string.h"#include "ctype.h"#include "stdlib.h"#include "math.h"#include "time.h"#define OK 1#define ERROR 0#define TRUE 1#define FALSE 0#define MAXSIZE 20 /* 存储空间初始分配量 */typedef int Status;/* Status是函数的类型,其值是函数结果状态代码,如OK等 */typedef int ElemType;/* ElemType类型根据实际情况而定,这里假设为int */Status visit(ElemType c){printf("%d ",c);return OK;}typedef struct Node{ElemType data;struct Node *next;}Node;typedef struct Node *LinkList; /* 定义LinkList *//* 初始化链式线性表 */Status InitList(LinkList *L){*L=(LinkList)malloc(sizeof(Node)); /* 产生头结点,并使L指向此头结点 */if(!(*L)) /* 存储分配失败 */return ERROR;(*L)->next=NULL; /* 指针域为空 */return OK;}/* 初始条件:链式线性表L已存在。操作结果:若L为空表,则返回TRUE,否则返回FALSE */Status ListEmpty(LinkList L){if(L->next)return FALSE;elsereturn TRUE;}/* 初始条件:链式线性表L已存在。操作结果:将L重置为空表 */Status ClearList(LinkList *L){LinkList p,q;p=(*L)->next; /* p指向第一个结点 */while(p) /* 没到表尾 */{q=p->next;free(p);p=q;}(*L)->next=NULL; /* 头结点指针域为空 */return OK;}/* 初始条件:链式线性表L已存在。操作结果:返回L中数据元素个数 */int ListLength(LinkList L){int i=0;LinkList p=L->next; /* p指向第一个结点 */while(p){i++;p=p->next;}return i;}/* 初始条件:链式线性表L已存在,1≤i≤ListLength(L) *//* 操作结果:用e返回L中第i个数据元素的值 */Status GetElem(LinkList L,int i,ElemType *e){int j;LinkList p; /* 声明一结点p */p = L->next; /* 让p指向链表L的第一个结点 */j = 1; /* j为计数器 */while (p && j<i) /* p不为空或者计数器j还没有等于i时,循环继续 */{p = p->next; /* 让p指向下一个结点 */++j;}if ( !p || j>i )return ERROR; /* 第i个元素不存在 */*e = p->data; /* 取第i个元素的数据 */return OK;}/* 初始条件:链式线性表L已存在 *//* 操作结果:返回L中第1个与e满足关系的数据元素的位序。 *//* 若这样的数据元素不存在,则返回值为0 */int LocateElem(LinkList L,ElemType e){int i=0;LinkList p=L->next;while(p){i++;if(p->data==e) /* 找到这样的数据元素 */return i;p=p->next;}return 0;}/* 初始条件:链式线性表L已存在,1≤i≤ListLength(L), *//* 操作结果:在L中第i个位置之前插入新的数据元素e,L的长度加1 */Status ListInsert(LinkList *L,int i,ElemType e){int j;LinkList p,s;p = *L;j = 1;while (p && j < i) /* 寻找第i个结点 */{p = p->next;++j;}if (!p || j > i)return ERROR; /* 第i个元素不存在 */s = (LinkList)malloc(sizeof(Node)); /* 生成新结点(C语言标准函数) */s->data = e;s->next = p->next; /* 将p的后继结点赋值给s的后继 */p->next = s; /* 将s赋值给p的后继 */return OK;}/* 初始条件:链式线性表L已存在,1≤i≤ListLength(L) *//* 操作结果:删除L的第i个数据元素,并用e返回其值,L的长度减1 */Status ListDelete(LinkList *L,int i,ElemType *e){int j;LinkList p,q;p = *L;j = 1;while (p->next && j < i) /* 遍历寻找第i个元素 */{p = p->next;++j;}if (!(p->next) || j > i)return ERROR; /* 第i个元素不存在 */q = p->next;p->next = q->next; /* 将q的后继赋值给p的后继 */*e = q->data; /* 将q结点中的数据给e */free(q); /* 让系统回收此结点,释放内存 */return OK;}/* 初始条件:链式线性表L已存在 *//* 操作结果:依次对L的每个数据元素输出 */Status ListTraverse(LinkList L){LinkList p=L->next;while(p){visit(p->data);p=p->next;}printf("\n");return OK;}/* 随机产生n个元素的值,建立带表头结点的单链线性表L(头插法) */void CreateListHead(LinkList *L, int n){LinkList p;int i;srand(time(0)); /* 初始化随机数种子 */*L = (LinkList)malloc(sizeof(Node));(*L)->next = NULL; /* 先建立一个带头结点的单链表 */for (i=0; i<n; i++){p = (LinkList)malloc(sizeof(Node)); /* 生成新结点 */p->data = rand()%100+1; /* 随机生成100以内的数字 */p->next = (*L)->next;(*L)->next = p; /* 插入到表头 */}}/* 随机产生n个元素的值,建立带表头结点的单链线性表L(尾插法) */void CreateListTail(LinkList *L, int n){LinkList p,r;int i;srand(time(0)); /* 初始化随机数种子 */*L = (LinkList)malloc(sizeof(Node)); /* L为整个线性表 */r=*L; /* r为指向尾部的结点 */for (i=0; i<n; i++){p = (Node *)malloc(sizeof(Node)); /* 生成新结点 */p->data = rand()%100+1; /* 随机生成100以内的数字 */r->next=p; /* 将表尾终端结点的指针指向新结点 */r = p; /* 将当前的新结点定义为表尾终端结点 */}r->next = NULL; /* 表示当前链表结束 */}int main(){LinkList L;ElemType e;Status i;int j,k;i=InitList(&L);printf("初始化L后:ListLength(L)=%d\n",ListLength(L));for(j=1;j<=5;j++)i=ListInsert(&L,1,j);printf("在L的表头依次插入1~5后:L.data=");ListTraverse(L);printf("ListLength(L)=%d \n",ListLength(L));i=ListEmpty(L);printf("L是否空:i=%d(1:是 0:否)\n",i);i=ClearList(&L);printf("清空L后:ListLength(L)=%d\n",ListLength(L));i=ListEmpty(L);printf("L是否空:i=%d(1:是 0:否)\n",i);for(j=1;j<=10;j++)ListInsert(&L,j,j);printf("在L的表尾依次插入1~10后:L.data=");ListTraverse(L);printf("ListLength(L)=%d \n",ListLength(L));ListInsert(&L,1,0);printf("在L的表头插入0后:L.data=");ListTraverse(L);printf("ListLength(L)=%d \n",ListLength(L));GetElem(L,5,&e);printf("第5个元素的值为:%d\n",e);for(j=3;j<=4;j++){k=LocateElem(L,j);if(k)printf("第%d个元素的值为%d\n",k,j);elseprintf("没有值为%d的元素\n",j);}k=ListLength(L); /* k为表长 */for(j=k+1;j>=k;j--){i=ListDelete(&L,j,&e); /* 删除第j个数据 */if(i==ERROR)printf("删除第%d个数据失败\n",j);elseprintf("删除第%d个的元素值为:%d\n",j,e);}printf("依次输出L的元素:");ListTraverse(L);j=5;ListDelete(&L,j,&e); /* 删除第5个数据 */printf("删除第%d个的元素值为:%d\n",j,e);printf("依次输出L的元素:");ListTraverse(L);i=ClearList(&L);printf("\n清空L后:ListLength(L)=%d\n",ListLength(L));CreateListHead(&L,20);printf("整体创建L的元素(头插法):");ListTraverse(L);i=ClearList(&L);printf("\n删除L后:ListLength(L)=%d\n",ListLength(L));CreateListTail(&L,20);printf("整体创建L的元素(尾插法):");ListTraverse(L);return 0;}
输出
初始化L后:ListLength(L)=0在L的表头依次插入1~5后:L.data=5 4 3 2 1ListLength(L)=5L是否空:i=0(1:是 0:否)清空L后:ListLength(L)=0L是否空:i=1(1:是 0:否)在L的表尾依次插入1~10后:L.data=1 2 3 4 5 6 7 8 9 10ListLength(L)=10在L的表头插入0后:L.data=0 1 2 3 4 5 6 7 8 9 10ListLength(L)=11第5个元素的值为:4第4个元素的值为3第5个元素的值为4删除第12个数据失败删除第11个的元素值为:10依次输出L的元素:0 1 2 3 4 5 6 7 8 9删除第5个的元素值为:4依次输出L的元素:0 1 2 3 5 6 7 8 9清空L后:ListLength(L)=0整体创建L的元素(头插法):82 14 68 79 56 3 54 61 5 33 33 100 15 2 6 27 9 8 97 35删除L后:ListLength(L)=0整体创建L的元素(尾插法):35 97 8 9 27 6 2 15 100 33 33 5 61 54 3 56 79 68 14 82
2.5 线性表类型的实现—-链式存储结构
2.5.1 一、单链表
线性表的链式存储结构 : 用一组地址任意的存储单元存放线性表中的数据元素。
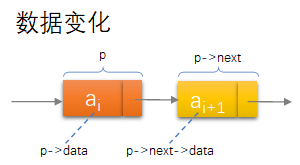
- 数据元素的存储映像,也称结点,包括:
- 数据域:元素本身信息
- 指针域:指示直接后继的存储位置

以元素(数据元素的映象)+ 指针(指示后继元素存储位置)= 结点(表示数据元素 或 数据元素的映象),以“结点的序列”表示线性表称作链表。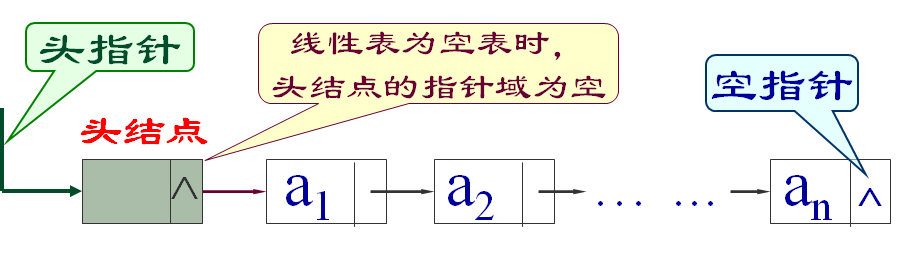
以线性表中第一个数据元素的存储地址作为线性表的地址,称作线性表的头指针。
有时为了操作方便,在第一个结点之前虚加一个“头结点”,以指向头结点的指针为链表的头指针。
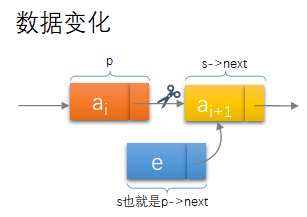
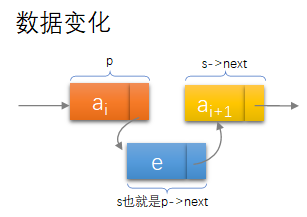
单链表元素插入
Status ListInsert(LinkList *L,int i,ElemType e){int j;LinkList p,s;p = *L;j = 1;while (p && j < i){p = p->next;++j;}if (!p || j > i)return ERROR;s = (LinkList)malloc(sizeof(Node));s->data = e;s->next = p->next;p->next = s;return OK;}
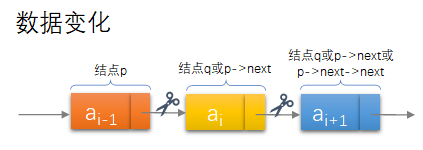
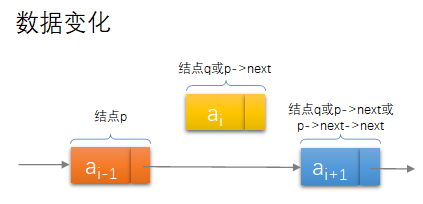
单链表元素删除
Status ListDelete(LinkList *L,int i,ElemType *e){int j;LinkList p,q;p = *L;j = 1;while (p->next && j < i){p = p->next;++j;}if (!(p->next) || j > i)return ERROR;q = p->next;p->next = q->next;*e = q->data;free(q);return OK;}
单链表的整表创建
/* 随机产生n个元素的值,建立带表头结点的单链线性表L(头插法) */void CreateListHead(LinkList *L, int n){LinkList p;int i;srand(time(0)); /* 初始化随机数种子 */*L = (LinkList)malloc(sizeof(Node));(*L)->next = NULL; /* 先建立一个带头结点的单链表 */for (i=0; i<n; i++){p = (LinkList)malloc(sizeof(Node)); /* 生成新结点 */p->data = rand()%100+1; /* 随机生成100以内的数字 */p->next = (*L)->next;(*L)->next = p; /* 插入到表头 */}}/* 随机产生n个元素的值,建立带表头结点的单链线性表L(尾插法) */void CreateListTail(LinkList *L, int n){LinkList p,r;int i;srand(time(0)); /* 初始化随机数种子 */*L = (LinkList)malloc(sizeof(Node)); /* L为整个线性表 */r=*L; /* r为指向尾部的结点 */for (i=0; i<n; i++){p = (Node *)malloc(sizeof(Node)); /* 生成新结点 */p->data = rand()%100+1; /* 随机生成100以内的数字 */r->next=p; /* 将表尾终端结点的指针指向新结点 */r = p; /* 将当前的新结点定义为表尾终端结点 */}r->next = NULL; /* 表示当前链表结束 */}
单链表整表删除
/* 初始条件:链式线性表L已存在。操作结果:将L重置为空表 */Status ClearList(LinkList *L){LinkList p,q;p=(*L)->next; /* p指向第一个结点 */while(p) /* 没到表尾 */{q=p->next;free(p);p=q;}(*L)->next=NULL; /* 头结点指针域为空 */return OK;}
2.5.2 单链表结构与顺序存储结构的优缺点
存储分配方式
顺序存储结构:一段连续存储单元依次存储线性的数据元素
链式存储结构(单链表):一组任意的存储单元存放线性表的元素
时间性能
查找:
顺序存储结构O(1)
单链表O(n)
插入与删除
顺序存储结构:需要平均移动表长一半的元素,时间复杂度为O(n)
单链表:找出位置的指针后,插入和删除时间复杂度仅为O(1)
空间性能
顺序存储结构:需要预分配存储空间,分大了,浪费。分小了,易发生上溢。
单链表:不需要分配存储空间,只要有就可以分配,元素个数也不受限制。
2.5.3 二,静态链表
用数组描述的链表叫做静态链表
#include "string.h"#include "ctype.h"#include "stdio.h"#include "stdlib.h"#include "math.h"#include "time.h"#define OK 1#define ERROR 0#define TRUE 1#define FALSE 0#define MAXSIZE 1000 /* 存储空间初始分配量 */typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */typedef char ElemType; /* ElemType类型根据实际情况而定,这里假设为char */Status visit(ElemType c){printf("%c ",c);return OK;}/* 线性表的静态链表存储结构 */typedef struct{ElemType data;int cur; /* 游标(Cursor) ,为0时表示无指向 */} Component,StaticLinkList[MAXSIZE];/* 将一维数组space中各分量链成一个备用链表,space[0].cur为头指针,"0"表示空指针 */Status InitList(StaticLinkList space){int i;for (i=0; i<MAXSIZE-1; i++)space[i].cur = i+1;space[MAXSIZE-1].cur = 0; /* 目前静态链表为空,最后一个元素的cur为0 */return OK;}/* 若备用空间链表非空,则返回分配的结点下标,否则返回0 */int Malloc_SSL(StaticLinkList space){int i = space[0].cur; /* 当前数组第一个元素的cur存的值 *//* 就是要返回的第一个备用空闲的下标 */if (space[0]. cur)space[0]. cur = space[i].cur; /* 由于要拿出一个分量来使用了, *//* 所以我们就得把它的下一个 *//* 分量用来做备用 */return i;}/* 将下标为k的空闲结点回收到备用链表 */void Free_SSL(StaticLinkList space, int k){space[k].cur = space[0].cur; /* 把第一个元素的cur值赋给要删除的分量cur */space[0].cur = k; /* 把要删除的分量下标赋值给第一个元素的cur */}/* 初始条件:静态链表L已存在。操作结果:返回L中数据元素个数 */int ListLength(StaticLinkList L){int j=0;int i=L[MAXSIZE-1].cur;while(i){i=L[i].cur;j++;}return j;}/* 在L中第i个元素之前插入新的数据元素e */Status ListInsert(StaticLinkList L, int i, ElemType e){int j, k, l;k = MAXSIZE - 1; /* 注意k首先是最后一个元素的下标 */if (i < 1 || i > ListLength(L) + 1)return ERROR;j = Malloc_SSL(L); /* 获得空闲分量的下标 */if (j){L[j].data = e; /* 将数据赋值给此分量的data */for(l = 1; l <= i - 1; l++) /* 找到第i个元素之前的位置 */k = L[k].cur;L[j].cur = L[k].cur; /* 把第i个元素之前的cur赋值给新元素的cur */L[k].cur = j; /* 把新元素的下标赋值给第i个元素之前元素的ur */return OK;}return ERROR;}/* 删除在L中第i个数据元素 */Status ListDelete(StaticLinkList L, int i){int j, k;if (i < 1 || i > ListLength(L))return ERROR;k = MAXSIZE - 1;for (j = 1; j <= i - 1; j++)k = L[k].cur;j = L[k].cur;L[k].cur = L[j].cur;Free_SSL(L, j);return OK;}Status ListTraverse(StaticLinkList L){int j=0;int i=L[MAXSIZE-1].cur;while(i){visit(L[i].data);i=L[i].cur;j++;}return j;printf("\n");return OK;}int main(){StaticLinkList L;Status i;i=InitList(L);printf("初始化L后:L.length=%d\n",ListLength(L));i=ListInsert(L,1,'F');i=ListInsert(L,1,'E');i=ListInsert(L,1,'D');i=ListInsert(L,1,'B');i=ListInsert(L,1,'A');printf("\n在L的表头依次插入FEDBA后:\nL.data=");ListTraverse(L);i=ListInsert(L,3,'C');printf("\n在L的“B”与“D”之间插入“C”后:\nL.data=");ListTraverse(L);i=ListDelete(L,1);printf("\n在L的删除“A”后:\nL.data=");ListTraverse(L);printf("\n");return 0;}
输出
初始化L后:L.length=0在L的表头依次插入FEDBA后:L.data=A B D E F在L的“B”与“D”之间插入“C”后:L.data=A B C D E F在L的删除“A”后:L.data=B C D E F
静态链表的优缺点
优点:在插入和删除操作时,只需要修改游标,不需要移动元素,从而改进了在顺序存储结构中插入和删除操作需要移动大量元素的缺点。
缺点:没有解决连续存储带分配来的表长难以确定的问题。失去了链式存储结构随机存取的特性。
2.5.4 三,循环链表
代码示例
#include <stdio.h>#include <stdlib.h>typedef struct List{int data;struct List *next;} list, *p_list;void creat_list(list **p) //如果链表为空,则创建一个链表,指针域指向自己,否则寻找尾节点,将{ //将尾节点的指针域指向这个新节点,新节点的指针域指向头结点int item;list *temp;list *target;printf("输入节点的值,输入0结束\n");while (1){scanf("%d", &item);if (item == 0)break;if (*p == NULL) //如果输入的链表是空。则创建一个新的节点,使其next指针指向自己 (*head)->next=*head;{*p = (list *)malloc(sizeof(list));if (!*p)exit(0);(*p)->data = item;(*p)->next = *p;}else //输入的链表不是空的,寻找链表的尾节点,使尾节点的next=新节点。新节点的next指向头节点{for (target = *p; target->next != *p; target = target->next); //寻找尾节点temp = (list *)malloc(sizeof(list));if (!temp)exit(0);temp->data = item;temp->next = *p; //新节点指向头节点target->next = temp; //尾节点指向新节点}}}void insert(list **pNode, int place, int num) //链表的插入{list *temp, *target;int i;if (place == 1) //如果输入的数字是1,表示要插入头节点。应该特殊处理{ //首先找到尾节点,让后让新节点的next指向头节点,尾节点指向新的头节点,在让头指针指向temp。这要特别注意temp = (list *)malloc(sizeof(list));if (!temp)exit(0);temp->data = num;for (target = *pNode; target->next != *pNode; target = target->next);temp->next = *pNode;target->next = temp;*pNode = temp; //特别注意}else //在其他的地方插入节点。 同样先找到要插入的位置,如果位置超出链表的长度,自动插入队尾。 tar new 原来是2{ //找到要插入位置的前一个节点target,让target->next=temp,插入节点的前驱指向新节点,新节点指向target->next的地址 1 2 3for (i = 1, target = *pNode; target->next != *pNode && i != place - 1; target = target->next, i++);temp = (list *)malloc(sizeof(list));temp->data = num;temp->next = target->next;target->next = temp;}}void Delete(list **pNode, int place) //删除操作{list *temp, *target;int i;temp = *pNode;if (temp == NULL) //首先判断链表是否为空{printf("这是一个空指针 无法删除\n");return;}if (place == 1) //如果删除的是头节点{ //应当特殊处理,找到尾节点,使尾节点的next指向头节点的下一个节点 rear->next=(*head)->next;然后让新节点作为头节点,释放原来的头节点for (target = *pNode; target->next != *pNode; target = target->next);temp = *pNode;*pNode = (*pNode)->next;target->next = *pNode;free(temp);}else{ //删除其他节点for (i = 1, target = *pNode; target->next != *pNode && i != place - 1; target = target->next, i++); //首先找出尾节点if (target->next == *pNode) //判断要删除的位置是否大于链表长度,若大于链表长度,特殊处理直接删除尾节点{for (target = *pNode; target->next->next != *pNode; target = target->next); //找出尾节的前一个节点temp = target->next; // 尾节点的前一个节点直接指向头节点 释放原来的尾节点target->next = *pNode;printf("数字太大删除尾巴\n");free(temp);}else{temp = target->next; // 删除普通节点 找到要删除节点的前一个节点target,使target指向要删除节点的下一个节点 转存删除节点地址target->next = temp->next; // 然后释放这个节点free(temp);}}}int findval(list *pNode, int val) //寻找值{int i = 1;list *node;node = pNode;while (node->data != val && node->next != pNode){i++;node = node->next;}if (node->next == pNode && node->data != val) //尾节点指向头节点就跳出,因此还要检测一次为节点的data{return -1;}return i;}void show(list *p) //遍历,循环链表的遍历最好用do while语句 ,因为头节点就有值{list *temp;temp = p;do{printf("%5d", temp->data);temp = temp->next;} while (temp != p);printf("\n");}int main(){list *head = NULL;// list *val;int place, num;creat_list(&head);printf("原始的链表:");show(head);printf("输入要删除的位置:");scanf("%d", &place);Delete(&head, place);show(head);printf("输入要插入的位置和数据用空格隔开:");scanf("%d %d", &place, &num);insert(&head, place, num);show(head);printf("输入你想查找的值:");scanf("%d", &num);place = findval(head, num);if (place != -1)printf("找到的值的位置是place=%d\n", place);elseprintf("没找到值\n");return 0;}
测试输出
输入节点的值,输入0结束1 2 3 4 5 6 7 8 9 0原始的链表: 1 2 3 4 5 6 7 8 9输入要删除的位置:12 3 4 5 6 7 8 9输入要插入的位置和数据用空格隔开:2 6662 666 3 4 5 6 7 8 9输入你想查找的值:5找到的值的位置是place=5
2.5.5 四,双向链表
2.5.6 五,多项式的表示(待测试)
#include<iostream>#include<string>#include<fstream>using namespace std;#define ERROR 0typedef struct PNode {float coef; //系数int expn; //指数struct PNode *next;} PNode, *Polynomial;string head_1, head_2;int temp;char st = 'A';void CreatPolyn(Polynomial &P, int m) //算法2.18 多项式的创建{//输入m项的系数和指数,建立表示一个多项式的有序链表PPolynomial q, pre, s;int i;P = new PNode;P->next = NULL; //先建立一个带头结点的单链表char filename[20] = { 0 };cout << "请输入有关多项式p" << char(st + 32) << "系数和指数的数据文件名称(文件名+“.txt”,如Poly" << st << ".txt):" << endl;++st;gets(filename);fstream file;file.open(filename);if (!file) {cout << "未找到相关文件,无法打开!" << endl;exit(ERROR);}file >> head_1 >> head_2;while (!file.eof()){s = new PNode; //生成新结点file >> s->coef >> s->expn; //输入元素值pre = P; //pre用于保存q的前驱,初值为头结点q = P->next;while (q && q->expn < s->expn) //通过比较指数找到第一个大于输入项指数的项q{pre = q;q = q->next;} //whiles->next = q; //将输入项s插入到q和其前驱结点pre之间pre->next = s;}//forfile.close();} //CreatPolynvoid AddPolyn(Polynomial &Pa, Polynomial &Pb) //算法2.19 多项式的相加{//多项式加法:Pa=Pa+Pb,利用两个多项式的结点构成“和多项式”Polynomial r, p1, p2, p3;float sum;p1 = Pa->next;p2 = Pb->next; //p1和p2初值分别指向Pa和Pb的第一个结点p3 = Pa; //p3指向和多项式的当前结点,初值为Pawhile (p1 && p2) //p1和p2均非空{if (p1->expn == p2->expn) //指数相等{sum = p1->coef + p2->coef; //sum保存两项的系数和if (sum != 0) //系数和不为0{p1->coef = sum; //修改Pa当前结点p1的系数值为两项系数的和p3->next = p1;p3 = p1; //将修改后的Pa当前结点p1链在p3之后,p3指向p1p1 = p1->next; //p1指向后一项r = p2;p2 = p2->next;delete r; //删除Pb当前结点r} else //系数和为0{r = p1;p1 = p1->next;delete r; //删除Pb当前结点p1r = p2;p2 = p2->next;delete r; //删除Pb当前结点p2}} else if (p1->expn < p2->expn) //Pa当前结点p1的指数值小{p3->next = p1; //将p1链在p3之后p3 = p1; //p3指向p1p1 = p1->next; //p1指向后一项} else //Pa当前结点p2的指数值小{p3->next = p2; //将p2链在p3之后p3 = p2; //p3指向p2p2 = p2->next; //p2指向后一项}} //whilep3->next = p1 ? p1 : p2; //插入非空多项式的剩余段delete Pb; //释放Pb的头结点} //AddPolynint main() {Polynomial Pa, Pb;Polynomial p;int i;//创建多项式PaCreatPolyn(Pa, temp); //调用函数,输入Pa每一项的系数和指数//创建多项式PbCreatPolyn(Pb, temp); //调用函数,输入Pa每一项的系数和指数AddPolyn(Pa, Pb);cout << "多项式Pa和Pb相加后的结果是:\n";p = Pa->next;i = 0;while (p) //输出相加后的结果,每一项以x^n表示{if (i)cout << " + ";cout << "(" << p->coef << ") * x^" << p->expn;p = p->next;i = 1;}cout << endl;return 0;}
3. 第三章 栈和队列
3.1 栈
3.1.1 栈的抽象数据类型的定义
/*栈的抽象数据类型的定义*/ADT Stack{数据对象:D={a_i|a_i属于ElemSet,i=1,2,...,n,n>=0}数据关系:R1={<a_i-1,a_i>|a_i-1,a_i属于D,i=1,2,...,n}约定a_n端为栈顶,a_1端为栈底。基本操作:InitStack(&S)操作结果:构造一个空栈S。DestroyStack(&S)初始条件:栈S已存在。操作结果:栈S被销毁。ClearStack(&S)初始条件:栈S已存在。操作结果:将S清为空栈。StackEmpty(S)初始条件:栈S已存在。操作结果:若S为空栈,则返回TRUE,否则FALSE。StackLength(S)初始条件:栈S已存在。操作结果:返回S的元素个数,即栈的长度。GetTop(S,&e)初始条件:栈S已存在,并且非空。操作结果:用e返回S的栈顶元素。Push(&S,e)初始条件:栈S已存在。操作结果:插入e为新的栈顶元素。Pop(&S,&e)初始条件:栈S已存在且非空。操作结果:删除S栈顶元素,并用e返回其值。StackTraverse(S,visit())初始条件:栈S已存在且非空。操作结果:从栈底到栈顶依次对S的每个数据元素调用函数visit()。一旦visit()失败,则操作失败。}ADT Stack;
3.2 顺序栈的实现
#include "stdio.h"#include "stdlib.h"#include "math.h"#include "time.h"#define OK 1#define ERROR 0#define TRUE 1#define FALSE 0#define MAXSIZE 20 /* 存储空间初始分配量 */typedef int Status;typedef int SElemType; /* SElemType类型根据实际情况而定,这里假设为int *//* 顺序栈结构 */typedef struct{SElemType data[MAXSIZE];int top; /* 用于栈顶指针 */}SqStack;Status visit(SElemType c){printf("%d ",c);return OK;}/* 构造一个空栈S */Status InitStack(SqStack *S){/* S.data=(SElemType *)malloc(MAXSIZE*sizeof(SElemType)); */S->top=-1;return OK;}/* 把S置为空栈 */Status ClearStack(SqStack *S){S->top=-1;return OK;}/* 若栈S为空栈,则返回TRUE,否则返回FALSE */Status StackEmpty(SqStack S){if (S.top==-1)return TRUE;elsereturn FALSE;}/* 返回S的元素个数,即栈的长度 */int StackLength(SqStack S){return S.top+1;}/* 若栈不空,则用e返回S的栈顶元素,并返回OK;否则返回ERROR */Status GetTop(SqStack S,SElemType *e){if (S.top==-1)return ERROR;else*e=S.data[S.top];return OK;}/* 插入元素e为新的栈顶元素 */Status Push(SqStack *S,SElemType e){if(S->top == MAXSIZE -1) /* 栈满 */{return ERROR;}S->top++; /* 栈顶指针增加一 */S->data[S->top]=e; /* 将新插入元素赋值给栈顶空间 */return OK;}/* 若栈不空,则删除S的栈顶元素,用e返回其值,并返回OK;否则返回ERROR */Status Pop(SqStack *S,SElemType *e){if(S->top==-1)return ERROR;*e=S->data[S->top]; /* 将要删除的栈顶元素赋值给e */S->top--; /* 栈顶指针减一 */return OK;}/* 从栈底到栈顶依次对栈中每个元素显示 */Status StackTraverse(SqStack S){int i;i=0;while(i<=S.top){visit(S.data[i++]);}printf("\n");return OK;}int main(){int j;SqStack s;int e;if(InitStack(&s)==OK)for(j=1;j<=10;j++)Push(&s,j);printf("栈中元素依次为:");StackTraverse(s);Pop(&s,&e);printf("弹出的栈顶元素 e=%d\n",e);printf("栈空否:%d(1:空 0:否)\n",StackEmpty(s));GetTop(s,&e);printf("栈顶元素 e=%d 栈的长度为%d\n",e,StackLength(s));ClearStack(&s);printf("清空栈后,栈空否:%d(1:空 0:否)\n",StackEmpty(s));return 0;}
输出
栈中元素依次为:1 2 3 4 5 6 7 8 9 10弹出的栈顶元素 e=10栈空否:0(1:空 0:否)栈顶元素 e=9 栈的长度为9清空栈后,栈空否:1(1:空 0:否)
3.2.1 顺序存储进栈
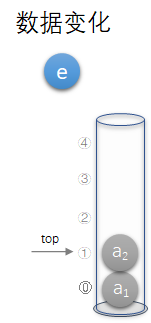
Status Push(SqStack *S,SElemType e){if(S->top == MAXSIZE -1){return ERROR;}S->top++;S->data[S->top]=e;return OK;}
3.2.2 顺序存储出栈
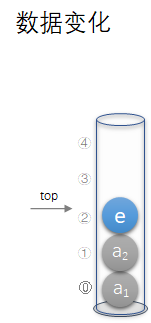
Status Pop(SqStack *S,SElemType *e){if(S->top==-1)return ERROR;*e=S->data[S->top];S->top--;return OK;}
3.3 两栈共享空间
#include "stdio.h"#include "stdlib.h"#include "math.h"#include "time.h"#define OK 1#define ERROR 0#define TRUE 1#define FALSE 0#define MAXSIZE 20 /* 存储空间初始分配量 */typedef int Status;typedef int SElemType; /* SElemType类型根据实际情况而定,这里假设为int *//* 两栈共享空间结构 */typedef struct{SElemType data[MAXSIZE];int top1; /* 栈1栈顶指针 */int top2; /* 栈2栈顶指针 */}SqDoubleStack;Status visit(SElemType c){printf("%d ",c);return OK;}/* 构造一个空栈S */Status InitStack(SqDoubleStack *S){S->top1=-1;S->top2=MAXSIZE;return OK;}/* 把S置为空栈 */Status ClearStack(SqDoubleStack *S){S->top1=-1;S->top2=MAXSIZE;return OK;}/* 若栈S为空栈,则返回TRUE,否则返回FALSE */Status StackEmpty(SqDoubleStack S){if (S.top1==-1 && S.top2==MAXSIZE)return TRUE;elsereturn FALSE;}/* 返回S的元素个数,即栈的长度 */int StackLength(SqDoubleStack S){return (S.top1+1)+(MAXSIZE-S.top2);}/* 插入元素e为新的栈顶元素 */Status Push(SqDoubleStack *S,SElemType e,int stackNumber){if (S->top1+1==S->top2) /* 栈已满,不能再push新元素了 */return ERROR;if (stackNumber==1) /* 栈1有元素进栈 */S->data[++S->top1]=e; /* 若是栈1则先top1+1后给数组元素赋值。 */else if (stackNumber==2) /* 栈2有元素进栈 */S->data[--S->top2]=e; /* 若是栈2则先top2-1后给数组元素赋值。 */return OK;}/* 若栈不空,则删除S的栈顶元素,用e返回其值,并返回OK;否则返回ERROR */Status Pop(SqDoubleStack *S,SElemType *e,int stackNumber){if (stackNumber==1){if (S->top1==-1)return ERROR; /* 说明栈1已经是空栈,溢出 */*e=S->data[S->top1--]; /* 将栈1的栈顶元素出栈 */}else if (stackNumber==2){if (S->top2==MAXSIZE)return ERROR; /* 说明栈2已经是空栈,溢出 */*e=S->data[S->top2++]; /* 将栈2的栈顶元素出栈 */}return OK;}Status StackTraverse(SqDoubleStack S){int i;i=0;while(i<=S.top1){visit(S.data[i++]);}i=S.top2;while(i<MAXSIZE){visit(S.data[i++]);}printf("\n");return OK;}int main(){int j;SqDoubleStack s;int e;if(InitStack(&s)==OK){for(j=1;j<=5;j++)Push(&s,j,1);for(j=MAXSIZE;j>=MAXSIZE-2;j--)Push(&s,j,2);}printf("栈中元素依次为:");StackTraverse(s);printf("当前栈中元素有:%d \n",StackLength(s));Pop(&s,&e,2);printf("弹出的栈顶元素 e=%d\n",e);printf("栈空否:%d(1:空 0:否)\n",StackEmpty(s));for(j=6;j<=MAXSIZE-2;j++)Push(&s,j,1);printf("栈中元素依次为:");StackTraverse(s);printf("栈满否:%d(1:否 0:满)\n",Push(&s,100,1));ClearStack(&s);printf("清空栈后,栈空否:%d(1:空 0:否)\n",StackEmpty(s));return 0;}
输出
栈中元素依次为:1 2 3 4 5 18 19 20当前栈中元素有:8弹出的栈顶元素 e=18栈空否:0(1:空 0:否)栈中元素依次为:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20栈满否:0(1:否 0:满)清空栈后,栈空否:1(1:空 0:否)
3.4 栈的链式存储结构
链栈的实现
#include "stdio.h"#include "stdlib.h"#include "math.h"#include "time.h"#define OK 1#define ERROR 0#define TRUE 1#define FALSE 0#define MAXSIZE 20 /* 存储空间初始分配量 */typedef int Status;typedef int SElemType; /* SElemType类型根据实际情况而定,这里假设为int *//* 链栈结构 */typedef struct StackNode{SElemType data;struct StackNode *next;}StackNode,*LinkStackPtr;typedef struct{LinkStackPtr top;int count;}LinkStack;Status visit(SElemType c){printf("%d ",c);return OK;}/* 构造一个空栈S */Status InitStack(LinkStack *S){S->top = (LinkStackPtr)malloc(sizeof(StackNode));if(!S->top)return ERROR;S->top=NULL;S->count=0;return OK;}/* 把S置为空栈 */Status ClearStack(LinkStack *S){LinkStackPtr p,q;p=S->top;while(p){q=p;p=p->next;free(q);}S->count=0;return OK;}/* 若栈S为空栈,则返回TRUE,否则返回FALSE */Status StackEmpty(LinkStack S){if (S.count==0)return TRUE;elsereturn FALSE;}/* 返回S的元素个数,即栈的长度 */int StackLength(LinkStack S){return S.count;}/* 若栈不空,则用e返回S的栈顶元素,并返回OK;否则返回ERROR */Status GetTop(LinkStack S,SElemType *e){if (S.top==NULL)return ERROR;else*e=S.top->data;return OK;}/* 插入元素e为新的栈顶元素 */Status Push(LinkStack *S,SElemType e){LinkStackPtr s=(LinkStackPtr)malloc(sizeof(StackNode));s->data=e;s->next=S->top; /* 把当前的栈顶元素赋值给新结点的直接后继,见图中① */S->top=s; /* 将新的结点s赋值给栈顶指针,见图中② */S->count++;return OK;}/* 若栈不空,则删除S的栈顶元素,用e返回其值,并返回OK;否则返回ERROR */Status Pop(LinkStack *S,SElemType *e){LinkStackPtr p;if(StackEmpty(*S))return ERROR;*e=S->top->data;p=S->top; /* 将栈顶结点赋值给p,见图中③ */S->top=S->top->next; /* 使得栈顶指针下移一位,指向后一结点,见图中④ */free(p); /* 释放结点p */S->count--;return OK;}Status StackTraverse(LinkStack S){LinkStackPtr p;p=S.top;while(p){visit(p->data);p=p->next;}printf("\n");return OK;}int main(){int j;LinkStack s;int e;if(InitStack(&s)==OK)for(j=1;j<=10;j++)Push(&s,j);printf("栈中元素依次为:");StackTraverse(s);Pop(&s,&e);printf("弹出的栈顶元素 e=%d\n",e);printf("栈空否:%d(1:空 0:否)\n",StackEmpty(s));GetTop(s,&e);printf("栈顶元素 e=%d 栈的长度为%d\n",e,StackLength(s));ClearStack(&s);printf("清空栈后,栈空否:%d(1:空 0:否)\n",StackEmpty(s));return 0;}
输出
栈中元素依次为:10 9 8 7 6 5 4 3 2 1弹出的栈顶元素 e=10栈空否:0(1:空 0:否)栈顶元素 e=9 栈的长度为9清空栈后,栈空否:1(1:空 0:否)
栈的应用——递归
斐波那契数列的实现
#include "stdio.h"/* 斐波那契的递归函数 */int Fbi(int i){if( i < 2 )return i == 0 ? 0 : 1;return Fbi(i - 1) + Fbi(i - 2); /* 这里Fbi就是函数自己,等于在调用自己 */}int main(){int i;int a[40];printf("迭代显示斐波那契数列:\n");a[0]=0;a[1]=1;printf("%d ",a[0]);printf("%d ",a[1]);for(i = 2;i < 40;i++){a[i] = a[i-1] + a[i-2];printf("%d ",a[i]);}printf("\n");printf("递归显示斐波那契数列:\n");for(i = 0;i < 40;i++)printf("%d ", Fbi(i));return 0;}
输出
迭代显示斐波那契数列:0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 10946 17711 28657 46368 75025 121393 196418 317811 514229 832040 1346269 2178309 3524578 5702887 9227465 14930352 24157817 3908816963245986递归显示斐波那契数列:0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 10946 17711 28657 46368 75025 121393 196418 317811 514229 832040 1346269 2178309 3524578 5702887 9227465 14930352 24157817 3908816963245986
递归:直接调用自己或通过一系列的调用语句间接地调用自己的函数,称作递归函数。
每个递归定义必须至少有一个条件,满足时递归不再进行,即不再引用自身而是返回值退出。
栈的应用——链栈实现表达式求值
/***链栈实现表达式求值***/#include<iostream>using namespace std;const char oper[7] = { '+', '-', '*', '/', '(', ')', '#' };#define OK 1#define ERROR 0#define OVERFLOW -2typedef char SElemType;typedef int Status;typedef struct SNode {int data;struct SNode *next;} SNode, *LinkStack;Status InitStack(LinkStack &S) {S = NULL;return OK;}bool StackEmpty(LinkStack S) {if (!S)return true;return false;}Status Push(LinkStack &S, SElemType e) {SNode *p = new SNode;if (!p) {return OVERFLOW;}p->data = e;p->next = S;S = p;return OK;}Status Pop(LinkStack &S, SElemType &e) {SNode *p;if (!S)return ERROR;e = S->data;p = S;S = S->next;delete p;return OK;}Status GetTop(LinkStack &S) {if (!S)return ERROR;return S->data;}bool In(char ch) {//判断ch是否为运算符for (int i = 0; i < 7; i++) {if (ch == oper[i]) {return true;}}return false;}char Precede(char theta1, char theta2) {//判断运算符优先级if ((theta1 == '(' && theta2 == ')') || (theta1 == '#' && theta2 == '#')) {return '=';} else if (theta1 == '(' || theta1 == '#' || theta2 == '(' || (theta1== '+' || theta1 == '-') && (theta2 == '*' || theta2 == '/')) {return '<';} elsereturn '>';}char Operate(char first, char theta, char second) {//计算两数运算结果switch (theta) {case '+':return (first - '0') + (second - '0') + 48;case '-':return (first - '0') - (second - '0') + 48;case '*':return (first - '0') * (second - '0') + 48;case '/':return (first - '0') / (second - '0') + 48;}return 0;}//算法3.22 表达式求值char EvaluateExpression() {//算术表达式求值的算符优先算法,设OPTR和OPND分别为运算符栈和操作数栈LinkStack OPTR, OPND;char ch, theta, a, b, x, top;InitStack(OPND); //初始化OPND栈InitStack(OPTR); //初始化OPTR栈Push(OPTR, '#'); //将表达式起始符“#”压入OPTR栈cin >> ch;while (ch != '#' || (GetTop(OPTR) != '#')) //表达式没有扫描完毕或OPTR的栈顶元素不为“#”{if (!In(ch)) {Push(OPND, ch);cin >> ch;} //ch不是运算符则进OPND栈elseswitch (Precede(GetTop(OPTR), ch)) //比较OPTR的栈顶元素和ch的优先级{case '<':Push(OPTR, ch);cin >> ch; //当前字符ch压入OPTR栈,读入下一字符chbreak;case '>':Pop(OPTR, theta); //弹出OPTR栈顶的运算符Pop(OPND, b);Pop(OPND, a); //弹出OPND栈顶的两个运算数Push(OPND, Operate(a, theta, b)); //将运算结果压入OPND栈break;case '=': //OPTR的栈顶元素是“(”且ch是“)”Pop(OPTR, x);cin >> ch; //弹出OPTR栈顶的“(”,读入下一字符chbreak;} //switch} //whilereturn GetTop(OPND); //OPND栈顶元素即为表达式求值结果}int menu() {int c;cout << "0-9以内的多项式计算" << endl;cout << "1.计算" << endl;cout << "0.退出\n" << endl;cout << "选择:";cin >> c;return c;}int main() {while (1) {switch (menu()) {case 1: {cout << "请输入要计算的表达式(操作数和结果都在0-9的范围内,以#结束):" << endl;char res = EvaluateExpression();//算法3.22 表达式求值cout << "计算结果为" << res - 48 << endl << endl;}break;case 0:cout << "退出成功\n" << endl;exit(0);default:break;}}return 0;}
输出
0-9以内的多项式计算1.计算0.退出选择:1请输入要计算的表达式(操作数和结果都在0-9的范围内,以#结束):((6*(8+9))+(8*(7+9)))#计算结果为-260-9以内的多项式计算1.计算0.退出选择:0退出成功
后缀(逆波兰)表示法的定义
中缀表达式转后缀表达式
栈的应用——链栈实现数制的转换
/***链栈实现数制的转换***/#include<iostream>using namespace std;#define OK 1#define ERROR 0#define OVERFLOW -2typedef int Status;typedef struct SNode {int data;struct SNode *next;} SNode, *LinkStack;Status InitStack(LinkStack &S) {S = NULL;return OK;}bool StackEmpty(LinkStack S) {if (!S)return true;return false;}Status Push(LinkStack &S, int e) {LinkStack p;p = new SNode;if (!p) {return OVERFLOW;}p->data = e;p->next = S;S = p;return OK;}Status Pop(LinkStack &S, int &e) {LinkStack p;if (!S)return ERROR;e = S->data;p = S;S = S->next;delete p;return OK;}//算法3.20 数制的转换(链栈实现)void conversion(int N) {//对于任意一个非负十进制数,打印输出与其等值的八进制数int e;LinkStack S;InitStack(S); //初始化空栈Swhile (N) //当N非零时,循环{Push(S, N % 8); //把N与8求余得到的八进制数压入栈SN = N / 8; //N更新为N与8的商}while (!StackEmpty(S)) //当栈S非空时,循环{Pop(S, e); //弹出栈顶元素ecout << e; //输出e}}int main() {//对于输入的任意一个非负十进制数,打印输出与其等值的八进制数int n, e;cout << "输入一个非负十进制数:" << endl;cin >> n;conversion(n);return 0;}
输出
输入一个非负十进制数:8881570
栈的应用——链栈实现括号匹配
/***链栈实现括号匹配***/#include<iostream>using namespace std;#define OK 1#define ERROR 0#define OVERFLOW -2typedef char SElemType;typedef int Status;typedef struct SNode {int data;struct SNode *next;} SNode, *LinkStack;Status InitStack(LinkStack &S) {S = NULL;return OK;}bool StackEmpty(LinkStack S) {if (!S)return true;return false;}Status Push(LinkStack &S, SElemType e) {SNode *p = new SNode;if (!p) {return OVERFLOW;}p->data = e;p->next = S;S = p;return OK;}Status Pop(LinkStack &S, SElemType &e) {SNode *p;if (!S)return ERROR;e = S->data;p = S;S = S->next;delete p;return OK;}Status GetTop(LinkStack &S) {if (!S)return ERROR;return S->data;}//算法3.21 括号的匹配Status Matching() {//检验表达式中所含括号是否正确匹配,如果匹配,则返回true,否则返回false//表达式以“#”结束char ch;SElemType x;LinkStack S;InitStack(S); //初始化空栈int flag = 1; //标记匹配结果以控制循环及返回结果cin >> ch; //读入第一个字符while (ch != '#' && flag) //假设表达式以“#”结尾{switch (ch) {case '[' :case '(': //若是左括号,则将其压入栈Push(S, ch);break;case ')': //若是“)”,则根据当前栈顶元素的值分情况考虑if (!StackEmpty(S) && GetTop(S) == '(')Pop(S, x); //若栈非空且栈顶元素是“(”,则正确匹配elseflag = 0; //若栈空或栈顶元素不是“(”,则错误失败break;case ']': //若是“]”,则根据当前栈顶元素的值分情况考虑if (!StackEmpty(S) && GetTop(S) == '[')Pop(S, x); //若栈非空且栈顶元素是“[”,则正确匹配elseflag = 0; //若栈空或栈顶元素不是“[”,则错误匹配break;} //switchcin >> ch; //继续读入下一个字符} //whileif (StackEmpty(S) && flag)return true; //匹配成功elsereturn false; //匹配失败}int main() {LinkStack S;cout << "请输入待匹配的表达式,以“#”结束:" << endl;int flag = (int) Matching();if (flag)cout << "括号匹配成功!" << endl;elsecout << "括号匹配失败!" << endl;return 0;}
输出(两次测试)
PS F:\Study\c_study\study001\栈与队列> cd "f:\Study\c_study\study001\栈与队列\" ; if ($?) { g++ 链栈实现括号匹配.cpp -o 链栈实现括号匹配 } ; if ($?) { .\链栈实现括号匹配 }请输入待匹配的表达式,以“#”结束:7*(6+7)+(8*(5+6)+7*(9+6))#括号匹配成功!PS F:\Study\c_study\study001\栈与队列> cd "f:\Study\c_study\study001\栈与队列\" ; if ($?) { g++ 链栈实现括号匹配.cpp -o 链栈实现括号匹配 } ; if ($?) { .\链栈实现括号匹配 }请输入待匹配的表达式,以“#”结束:(5+6*(4+6)*(8+9)))#括号匹配失败!
3.5 队列
队列:只允许在一端进行插入操作,而在另一端进行删除操作的线性表。
/*队列的抽象数据类型的定义*/ADT Queue{数据对象:D={a_i|a_i属于ElemSet,i=1,2,...,n,n>=0}数据关系:R1={<a_i-1,a_i>|a_i-1,a_i属于D,i=1,2,...,n}约定a_n端为队列头,a_1端为队列尾。基本操作:InitQueue(&Q)操作结果:构造一个空队列Q。DestroyQueue(&Q)初始条件:队列Q已存在。操作结果:队列Q被销毁,不再存在。ClearQueue(&Q)初始条件:队列Q已存在。操作结果:将Q清为空队列。QueueEmpty(Q)初始条件:队列Q已存在。操作结果:若Q为空队列,则返回TRUE,否则FALSE。QueueLength(Q)初始条件:队列Q已存在。操作结果:返回Q的元素个数,即队列的长度。GetHead(Q,&e)初始条件:队列Q已存在且非空。操作结果:用e返回Q的头元素。EnQueue(&Q,e)初始条件:队列Q已存在。操作结果:插入e为Q的新的队尾元素。DeQueue(&Q,&e)初始条件:队列Q已存在且非空。操作结果:删除Q的队头元素,并用e返回其值QueueTraverse(Q,visit())初始条件:队列Q已存在且非空。操作结果:从队头到队尾,依次对Q每个数据元素调用函数visit()。一旦visit()失败,则操作失败。}ADT Queue
链式存储进队列
Status EnQueue(LinkQueue *Q,QElemType e){QueuePtr s=(QueuePtr)malloc(sizeof(QNode));if(!s)exit(OVERFLOW);s->data=e;s->next=NULL;Q->rear->next=s;Q->rear=s;return OK;}
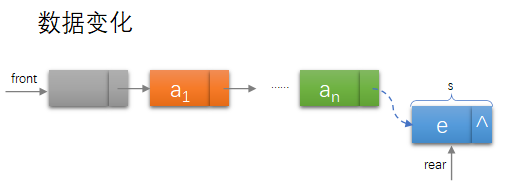
链式存储出队列
Status DeQueue(LinkQueue *Q,QElemType *e){QueuePtr p;if(Q->front==Q->rear)return ERROR;p=Q->front->next;*e=p->data;Q->front->next=p->next;if(Q->rear==p)Q->rear=Q->front;free(p);return OK;}
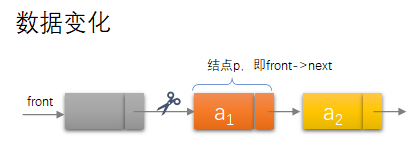
3.5.1 链队列
#include "stdio.h"#include "stdlib.h"#include "math.h"#include "time.h"#define OK 1#define ERROR 0#define TRUE 1#define FALSE 0#define MAXSIZE 20 /* 存储空间初始分配量 */typedef int Status;typedef int QElemType; /* QElemType类型根据实际情况而定,这里假设为int */typedef struct QNode /* 结点结构 */{QElemType data;struct QNode *next;}QNode,*QueuePtr;typedef struct /* 队列的链表结构 */{QueuePtr front,rear; /* 队头、队尾指针 */}LinkQueue;Status visit(QElemType c){printf("%d ",c);return OK;}/* 构造一个空队列Q */Status InitQueue(LinkQueue *Q){Q->front=Q->rear=(QueuePtr)malloc(sizeof(QNode));if(!Q->front)exit(OVERFLOW);Q->front->next=NULL;return OK;}/* 销毁队列Q */Status DestroyQueue(LinkQueue *Q){while(Q->front){Q->rear=Q->front->next;free(Q->front);Q->front=Q->rear;}return OK;}/* 将Q清为空队列 */Status ClearQueue(LinkQueue *Q){QueuePtr p,q;Q->rear=Q->front;p=Q->front->next;Q->front->next=NULL;while(p){q=p;p=p->next;free(q);}return OK;}/* 若Q为空队列,则返回TRUE,否则返回FALSE */Status QueueEmpty(LinkQueue Q){if(Q.front==Q.rear)return TRUE;elsereturn FALSE;}/* 求队列的长度 */int QueueLength(LinkQueue Q){int i=0;QueuePtr p;p=Q.front;while(Q.rear!=p){i++;p=p->next;}return i;}/* 若队列不空,则用e返回Q的队头元素,并返回OK,否则返回ERROR */Status GetHead(LinkQueue Q,QElemType *e){QueuePtr p;if(Q.front==Q.rear)return ERROR;p=Q.front->next;*e=p->data;return OK;}/* 插入元素e为Q的新的队尾元素 */Status EnQueue(LinkQueue *Q,QElemType e){QueuePtr s=(QueuePtr)malloc(sizeof(QNode));if(!s) /* 存储分配失败 */exit(OVERFLOW);s->data=e;s->next=NULL;Q->rear->next=s; /* 把拥有元素e的新结点s赋值给原队尾结点的后继,见图中① */Q->rear=s; /* 把当前的s设置为队尾结点,rear指向s,见图中② */return OK;}/* 若队列不空,删除Q的队头元素,用e返回其值,并返回OK,否则返回ERROR */Status DeQueue(LinkQueue *Q,QElemType *e){QueuePtr p;if(Q->front==Q->rear)return ERROR;p=Q->front->next; /* 将欲删除的队头结点暂存给p,见图中① */*e=p->data; /* 将欲删除的队头结点的值赋值给e */Q->front->next=p->next;/* 将原队头结点的后继p->next赋值给头结点后继,见图中② */if(Q->rear==p) /* 若队头就是队尾,则删除后将rear指向头结点,见图中③ */Q->rear=Q->front;free(p);return OK;}/* 从队头到队尾依次对队列Q中每个元素输出 */Status QueueTraverse(LinkQueue Q){QueuePtr p;p=Q.front->next;while(p){visit(p->data);p=p->next;}printf("\n");return OK;}int main(){int i;QElemType d;LinkQueue q;i=InitQueue(&q);if(i)printf("成功地构造了一个空队列!\n");printf("是否空队列?%d(1:空 0:否) ",QueueEmpty(q));printf("队列的长度为%d\n",QueueLength(q));EnQueue(&q,-5);EnQueue(&q,5);EnQueue(&q,10);printf("插入3个元素(-5,5,10)后,队列的长度为%d\n",QueueLength(q));printf("是否空队列?%d(1:空 0:否) ",QueueEmpty(q));printf("队列的元素依次为:");QueueTraverse(q);i=GetHead(q,&d);if(i==OK)printf("队头元素是:%d\n",d);DeQueue(&q,&d);printf("删除了队头元素%d\n",d);i=GetHead(q,&d);if(i==OK)printf("新的队头元素是:%d\n",d);ClearQueue(&q);printf("清空队列后,q.front=%u q.rear=%u q.front->next=%u\n",q.front,q.rear,q.front->next);DestroyQueue(&q);printf("销毁队列后,q.front=%u q.rear=%u\n",q.front, q.rear);return 0;}
输出
成功地构造了一个空队列!是否空队列?1(1:空 0:否) 队列的长度为0插入3个元素(-5,5,10)后,队列的长度为3是否空队列?0(1:空 0:否) 队列的元素依次为:-5 5 10队头元素是:-5删除了队头元素-5新的队头元素是:5清空队列后,q.front=12129376 q.rear=12129376 q.front->next=0销毁队列后,q.front=0 q.rear=0
3.5.2 循环队列
include “math.h”
include “time.h”
define OK 1
define ERROR 0
define TRUE 1
define FALSE 0
define MAXSIZE 20 / 存储空间初始分配量 /
typedef int Status; typedef int QElemType; / QElemType类型根据实际情况而定,这里假设为int /
/ 循环队列的顺序存储结构 / typedef struct { QElemType data[MAXSIZE]; int front; / 头指针 / int rear; / 尾指针,若队列不空,指向队列尾元素的下一个位置 / }SqQueue;
Status visit(QElemType c) { printf(“%d “,c); return OK; }
/ 初始化一个空队列Q / Status InitQueue(SqQueue *Q) { Q->front=0; Q->rear=0; return OK; }
/ 将Q清为空队列 / Status ClearQueue(SqQueue *Q) { Q->front=Q->rear=0; return OK; }
/ 若队列Q为空队列,则返回TRUE,否则返回FALSE / Status QueueEmpty(SqQueue Q) { if(Q.front==Q.rear) / 队列空的标志 / return TRUE; else return FALSE; }
/ 返回Q的元素个数,也就是队列的当前长度 / int QueueLength(SqQueue Q) { return (Q.rear-Q.front+MAXSIZE)%MAXSIZE; }
/ 若队列不空,则用e返回Q的队头元素,并返回OK,否则返回ERROR / Status GetHead(SqQueue Q,QElemType e) { if(Q.front==Q.rear) / 队列空 / return ERROR; e=Q.data[Q.front]; return OK; }
/ 若队列未满,则插入元素e为Q新的队尾元素 / Status EnQueue(SqQueue Q,QElemType e) { if ((Q->rear+1)%MAXSIZE == Q->front) / 队列满的判断 / return ERROR; Q->data[Q->rear]=e; / 将元素e赋值给队尾 / Q->rear=(Q->rear+1)%MAXSIZE;/ rear指针向后移一位置, / / 若到最后则转到数组头部 */ return OK; }
/ 若队列不空,则删除Q中队头元素,用e返回其值 / Status DeQueue(SqQueue Q,QElemType e) { if (Q->front == Q->rear) / 队列空的判断 / return ERROR; e=Q->data[Q->front]; / 将队头元素赋值给e / Q->front=(Q->front+1)%MAXSIZE; / front指针向后移一位置, / / 若到最后则转到数组头部 */ return OK; }
/ 从队头到队尾依次对队列Q中每个元素输出 / Status QueueTraverse(SqQueue Q) { int i; i=Q.front; while((i+Q.front)!=Q.rear) { visit(Q.data[i]); i=(i+1)%MAXSIZE; } printf(“\n”); return OK; }
int main() { Status j; int i=0,l; QElemType d; SqQueue Q; InitQueue(&Q); printf(“初始化队列后,队列空否?%u(1:空 0:否)\n”,QueueEmpty(Q));
printf("请输入整型队列元素(不超过%d个),-1为提前结束符: ",MAXSIZE-1);do{/* scanf("%d",&d); */d=i+100;if(d==-1)break;i++;EnQueue(&Q,d);}while(i<MAXSIZE-1);printf("队列长度为: %d\n",QueueLength(Q));printf("现在队列空否?%u(1:空 0:否)\n",QueueEmpty(Q));printf("连续%d次由队头删除元素,队尾插入元素:\n",MAXSIZE);for(l=1;l<=MAXSIZE;l++){DeQueue(&Q,&d);printf("删除的元素是%d,插入的元素:%d \n",d,l+1000);/* scanf("%d",&d); */d=l+1000;EnQueue(&Q,d);}l=QueueLength(Q);printf("现在队列中的元素为: \n");QueueTraverse(Q);printf("共向队尾插入了%d个元素\n",i+MAXSIZE);if(l-2>0)printf("现在由队头删除%d个元素:\n",l-2);while(QueueLength(Q)>2){DeQueue(&Q,&d);printf("删除的元素值为%d\n",d);}j=GetHead(Q,&d);if(j)printf("现在队头元素为: %d\n",d);ClearQueue(&Q);printf("清空队列后, 队列空否?%u(1:空 0:否)\n",QueueEmpty(Q));return 0;
}
输出```java初始化队列后,队列空否?1(1:空 0:否)请输入整型队列元素(不超过19个),-1为提前结束符: 队列长度为: 19现在队列空否?0(1:空 0:否)连续20次由队头删除元素,队尾插入元素:删除的元素是100,插入的元素:1001删除的元素是101,插入的元素:1002删除的元素是102,插入的元素:1003删除的元素是103,插入的元素:1004删除的元素是104,插入的元素:1005删除的元素是105,插入的元素:1006删除的元素是106,插入的元素:1007删除的元素是107,插入的元素:1008删除的元素是108,插入的元素:1009删除的元素是109,插入的元素:1010删除的元素是110,插入的元素:1011删除的元素是111,插入的元素:1012删除的元素是112,插入的元素:1013删除的元素是113,插入的元素:1014删除的元素是114,插入的元素:1015删除的元素是115,插入的元素:1016删除的元素是116,插入的元素:1017删除的元素是117,插入的元素:1018删除的元素是118,插入的元素:1019删除的元素是1001,插入的元素:1020现在队列中的元素为:1002 1003 1004 1005 1006 1007 1008 1009 1010 1011 1012 1013 1014 1015 1016 1017 1018 1019 1020共向队尾插入了39个元素现在由队头删除17个元素:删除的元素值为1002删除的元素值为1003删除的元素值为1004删除的元素值为1005删除的元素值为1006删除的元素值为1007删除的元素值为1008删除的元素值为1009删除的元素值为1010删除的元素值为1011删除的元素值为1012删除的元素值为1013删除的元素值为1014删除的元素值为1015删除的元素值为1016删除的元素值为1017删除的元素值为1018现在队头元素为: 1019清空队列后, 队列空否?1(1:空 0:否)
3.5.3 双端循环队列
- 判断队列为空? 当收尾指针相等,队列为空,head == tail
- 判断队列已满? 当尾指针的下一位等于头指针,队列已满,(tail + 1 + capacity) % capacity == head;
- 初始化队列时? 首尾指针从0开始, head = tail = 0
- 从头部插入数据? head 指针向前移动, head = (head - 1 + capacity) % capacity
- 从尾部插入数据? tail 指针向后移动, tail = (tail + 1) % capacity
- 从头部删除数据? head 指针向后移动, head = (head + 1) % capacity
- 从尾部删除数据? tail 指针向前移动, tail = (tail - 1 + capacity) % capacity
- 从尾部读取数据? 考虑头部插入(head 前移一位)和尾部插入(插入后,tail后移一位),所以读取data[(tail - 1 + capacity) % capacity]
- MyCircularDeque(k):构造函数,双端队列的大小为k。
- insertFront():将一个元素添加到双端队列头部。 如果操作成功返回 true。
- insertLast():将一个元素添加到双端队列尾部。如果操作成功返回 true。
- deleteFront():从双端队列头部删除一个元素。 如果操作成功返回 true。
- deleteLast():从双端队列尾部删除一个元素。如果操作成功返回 true。
- getFront():从双端队列头部获得一个元素。如果双端队列为空,返回 -1。
- getRear():获得双端队列的最后一个元素。 如果双端队列为空,返回 -1。
- isEmpty():检查双端队列是否为空。
- isFull():检查双端队列是否满了。

#include <stdio.h>#include <stdlib.h>typedef int bool;#define true 1#define false 0/*判断队列为空? 当收尾指针相等,队列为空,head == tail判断队列已满? 当尾指针的下一位等于头指针,队列已满,(tail + 1 + capacity) % capacity == head;初始化队列时? 首尾指针从0开始, head = tail = 0从头部插入数据? head 指针向前移动, head = (head - 1 + capacity) % capacity从尾部插入数据? tail 指针向后移动, tail = (tail + 1) % capacity从头部删除数据? head 指针向后移动, head = (head + 1) % capacity从尾部删除数据? tail 指针向前移动, tail = (tail - 1 + capacity) % capacity从尾部读取数据? 考虑头部插入(head 前移一位)和尾部插入(插入后,tail后移一位),所以读取data[(tail - 1 + capacity) % capacity]MyCircularDeque(k):构造函数,双端队列的大小为k。insertFront():将一个元素添加到双端队列头部。 如果操作成功返回 true。insertLast():将一个元素添加到双端队列尾部。如果操作成功返回 true。deleteFront():从双端队列头部删除一个元素。 如果操作成功返回 true。deleteLast():从双端队列尾部删除一个元素。如果操作成功返回 true。getFront():从双端队列头部获得一个元素。如果双端队列为空,返回 -1。getRear():获得双端队列的最后一个元素。 如果双端队列为空,返回 -1。isEmpty():检查双端队列是否为空。isFull():检查双端队列是否满了。*/typedef struct {int *data;int head;int tail;int capacity;} MyCircularDeque;// 建立双端循环队列及初始化MyCircularDeque* myCircularDequeCreate(int k) {MyCircularDeque *Dq = (MyCircularDeque *)malloc(sizeof(MyCircularDeque));if(!Dq)return NULL;Dq -> data = (int *)malloc(sizeof(int) * (k + 1));if(!Dq -> data)return NULL;Dq -> head = 0;Dq -> tail = 0;Dq -> capacity = k + 1;return Dq;}bool myCircularDequeIsFull(MyCircularDeque* obj);// 从队头插入数据,成功返回truebool myCircularDequeInsertFront(MyCircularDeque* obj, int value) {if(myCircularDequeIsFull(obj)) {return false;}obj -> head = (obj -> head - 1 + obj -> capacity) % obj -> capacity;obj -> data[obj -> head] = value;return true;}// 从队尾插入数据,成功返回truebool myCircularDequeInsertLast(MyCircularDeque* obj, int value) {if(myCircularDequeIsFull(obj)) {return false;}obj -> data[obj -> tail] = value;obj -> tail = (obj -> tail + 1) % obj -> capacity;return true;}bool myCircularDequeIsEmpty(MyCircularDeque* obj);// 从队头删除数据,成功返回truebool myCircularDequeDeleteFront(MyCircularDeque* obj) {if(myCircularDequeIsEmpty(obj)) {return false;}obj -> head = (obj -> head + 1) % obj -> capacity;return true;}//从队尾删除数据,成功返回truebool myCircularDequeDeleteLast(MyCircularDeque* obj) {if(myCircularDequeIsEmpty(obj)) {return false;}obj -> tail = (obj -> tail - 1 + obj -> capacity) % obj -> capacity;return true;}// 从deque获得前面的项目int myCircularDequeGetFront(MyCircularDeque* obj) {if(myCircularDequeIsEmpty(obj)) {return -1;}return obj -> data[obj -> head];}// 从deque获取最后一项int myCircularDequeGetRear(MyCircularDeque* obj) {if(myCircularDequeIsEmpty(obj)) {return -1;}return obj -> data[(obj -> tail - 1 + obj -> capacity) % obj -> capacity];}// 检查循环deque是否为空.bool myCircularDequeIsEmpty(MyCircularDeque* obj) {return (obj -> head == obj -> tail);}// 检查循环deque是否已满bool myCircularDequeIsFull(MyCircularDeque* obj) {return ((obj -> tail + 1) % obj -> capacity == obj -> head);}void myCircularDequeFree(MyCircularDeque* obj) {free(obj -> data);obj -> data = NULL;free(obj);obj = NULL;}int main(){MyCircularDeque *Dq;Dq=myCircularDequeCreate(20);myCircularDequeIsEmpty(Dq);for (int i = 0; i < 10; i++){myCircularDequeInsertLast(Dq,i);}for (int j = 0; j < 20; j++){printf("%d ",myCircularDequeGetRear(Dq));Dq->tail--;}printf("\n");myCircularDequeInsertFront(Dq,666);printf("从deque获得前面的项目:%d\n",myCircularDequeGetFront(Dq));myCircularDequeInsertLast(Dq,777);printf("从deque获取最后一项:%d\n",myCircularDequeGetRear(Dq));myCircularDequeDeleteFront(Dq);printf("从队头删除数据\n");printf("从deque获得前面的项目:%d\n",myCircularDequeGetFront(Dq));myCircularDequeDeleteLast(Dq);printf("从队尾删除数据\n");printf("从deque获取最后一项:%d\n",myCircularDequeGetRear(Dq));}
输出
从deque获得前面的项目:666从deque获取最后一项:778333539从队头删除数据从deque获得前面的项目:0从队尾删除数据从deque获取最后一项:1546793837