物联12002-翁修林-202004071-18(数据结构课设) - 图1
算法与数据结构课程设计报告
系（院）： 计算机科学学院
专业班级： 物联12002班
姓名： 翁修林
学号： 202004071
指导教师： 周张兰

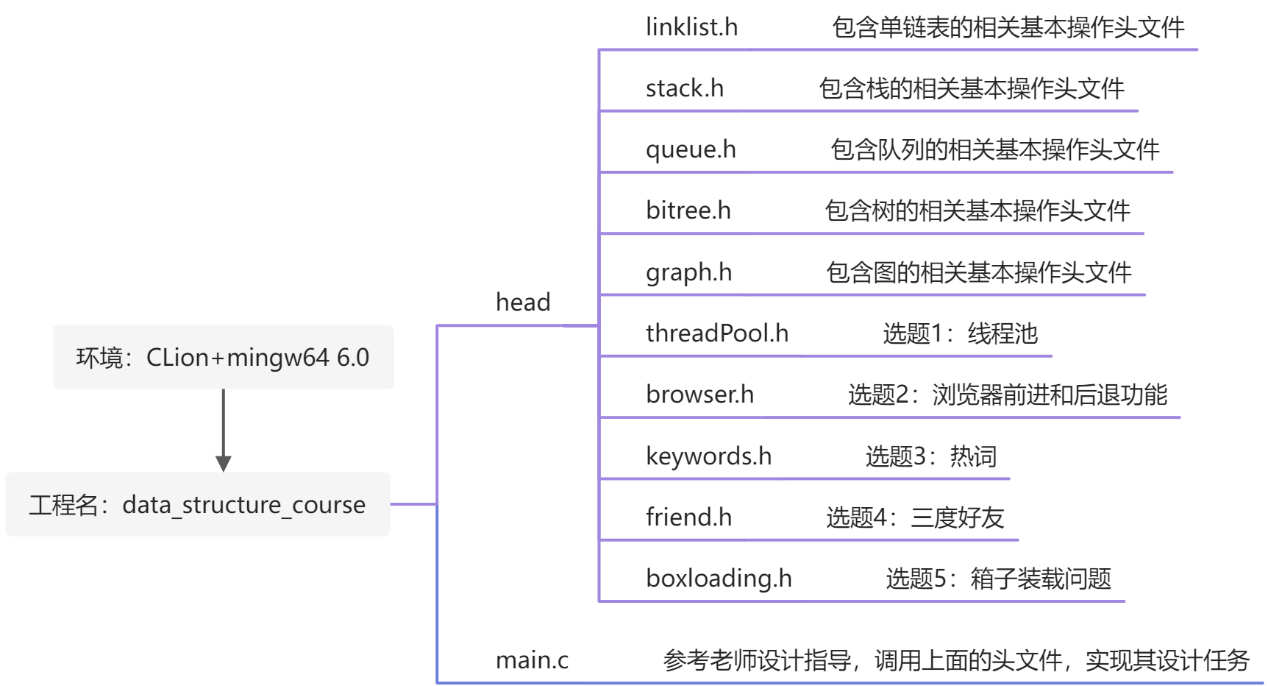
一.设计方案

物联12002-翁修林-202004071-18(数据结构课设) - 图2

二.实现过程

1．单链表的基本操作及应用

物联12002-翁修林-202004071-18(数据结构课设) - 图3

2．栈的基本操作及应用

物联12002-翁修林-202004071-18(数据结构课设) - 图4

3．队列的基本操作及应用

物联12002-翁修林-202004071-18(数据结构课设) - 图5

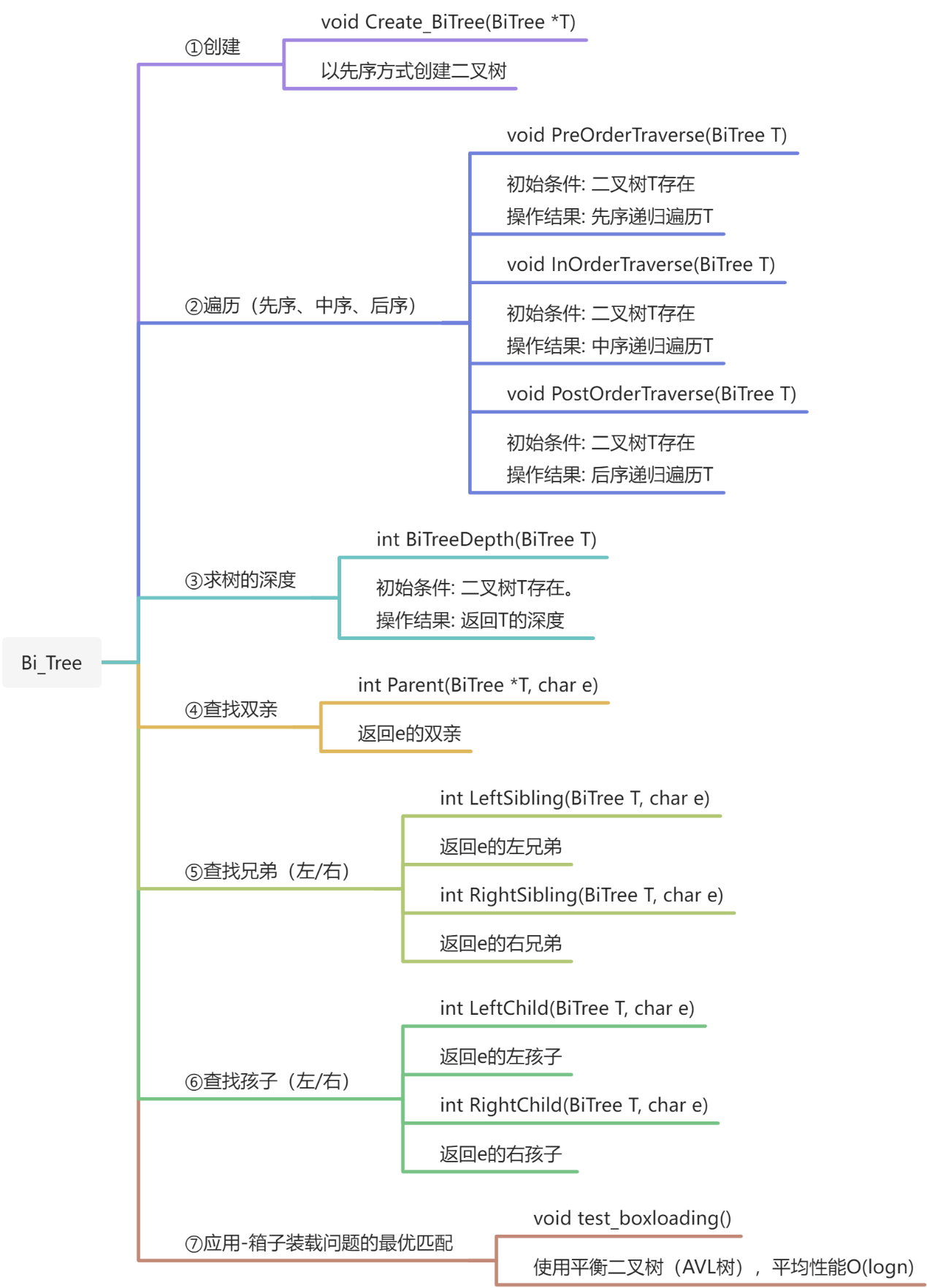
4．二叉树的基本操作及应用

物联12002-翁修林-202004071-18(数据结构课设) - 图6

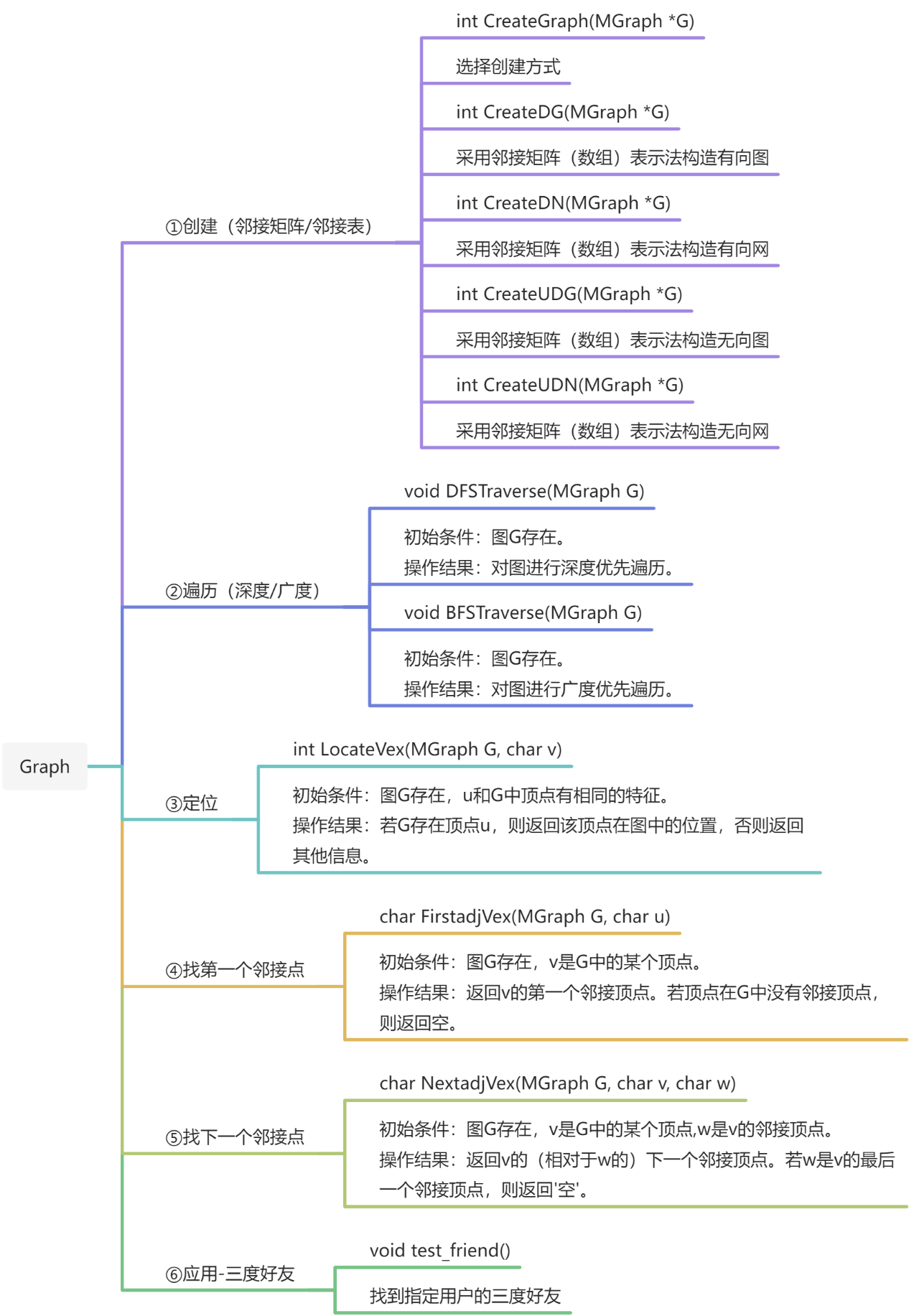
5．图的基本操作及应用

物联12002-翁修林-202004071-18(数据结构课设) - 图7

三.实现代码

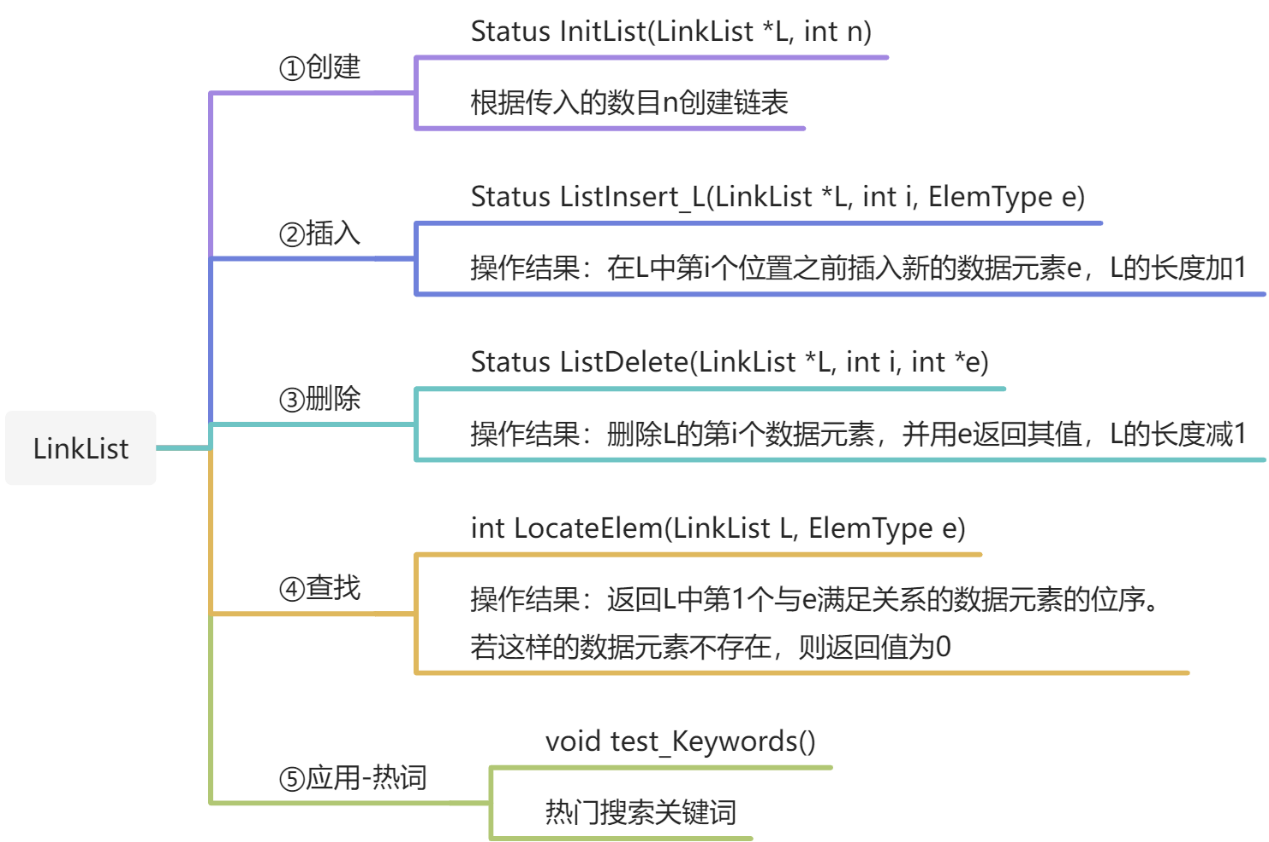
1. linklist链表

typedef struct Node
{
ElemType data;
struct Node next;
}Node;
typedef struct Node LinkList; / 定义LinkList /

/*
①创建
初始化链式线性表
根据传入的数目n创建链表
@param L
@param n
@return
/
Status InitList(LinkList L, int n)
{
L=(LinkList)malloc(sizeof(Node)); / 产生头结点,并使L指向此头结点 /
if(!(L)) / 存储分配失败 /
return ERROR;
(L)->next=NULL; / 指针域为空 /

for (int i = 0; i < n; ++i) {<br />        LinkList p=(LinkList) malloc(sizeof (Node));<br />        scanf("%d",&(p->data));<br />        p->next=(*L)->next;<br />        (*L)->next=p;<br />    }<br />    printf("\n!!链表创建成功!!\n");<br />    return OK;<br />}

/*
②插入
@brief
初始条件：链式线性表L已存在,1≤i≤ListLength(L)
操作结果：在L中第i个位置之前插入新的数据元素e，L的长度加1
@param L
@param i
@param e
@return Status
/
Status ListInsert_L(LinkList L, int i, ElemType e)
{
int j;
LinkList p,s;
p = L;
j = 1;
while (p && j < i)/ 寻找第i个结点 /
{
p = p->next;
++j;
}
if (!p || j > i)
return ERROR;/ 第i个元素不存在 /
s = (LinkList)malloc(sizeof(Node));/ 生成新结点(C语言标准函数) /
s->data = e;
s->next = p->next;/ 将p的后继结点赋值给s的后继 /
p->next = s;/ 将s赋值给p的后继 /
// printf(“\n!!链表第%d位插入%d成功!!\n”,i,e);
return OK;
}

/*
③删除
@brief
初始条件：链式线性表L已存在，1≤i≤ListLength(L)
操作结果：删除L的第i个数据元素，并用e返回其值，L的长度减1
@param L
@param i
@param e
@return Status
/
Status ListDelete(LinkList L, int i, int e)
{
// printf(“%d\n”,i);
int j;
LinkList p,q;
p = L;
j = 1;
while (p->next && j < i)/ 遍历寻找第i个元素 /
{
p = p->next;
++j;
}
if (!(p->next) || j > i)
return ERROR;/ 第i个元素不存在 /
q = p->next;
p->next = q->next;/ 将q的后继赋值给p的后继 /
e = q->data;/ 将q结点中的数据给e /
free(q);/ 让系统回收此结点，释放内存 /
// printf(“\n!!链表第%d,值为%d位删除成功!!\n”,i,*e);
return OK;
}

/*
④查找
@brief
初始条件：链式线性表L已存在
操作结果：返回L中第1个与e满足关系的数据元素的位序。
若这样的数据元素不存在，则返回值为0
@param L
@param e
@return int
/
int LocateElem(LinkList L, ElemType e)
{
int i=0;
LinkList p=L->next;
while(p)
{
i++;
if(p->data==e)/ 找到这样的数据元素 /
{
// printf(“\n!!链表中查找%d成功!!\n”,e);
return i;
}
p=p->next;
}
return 0;
}

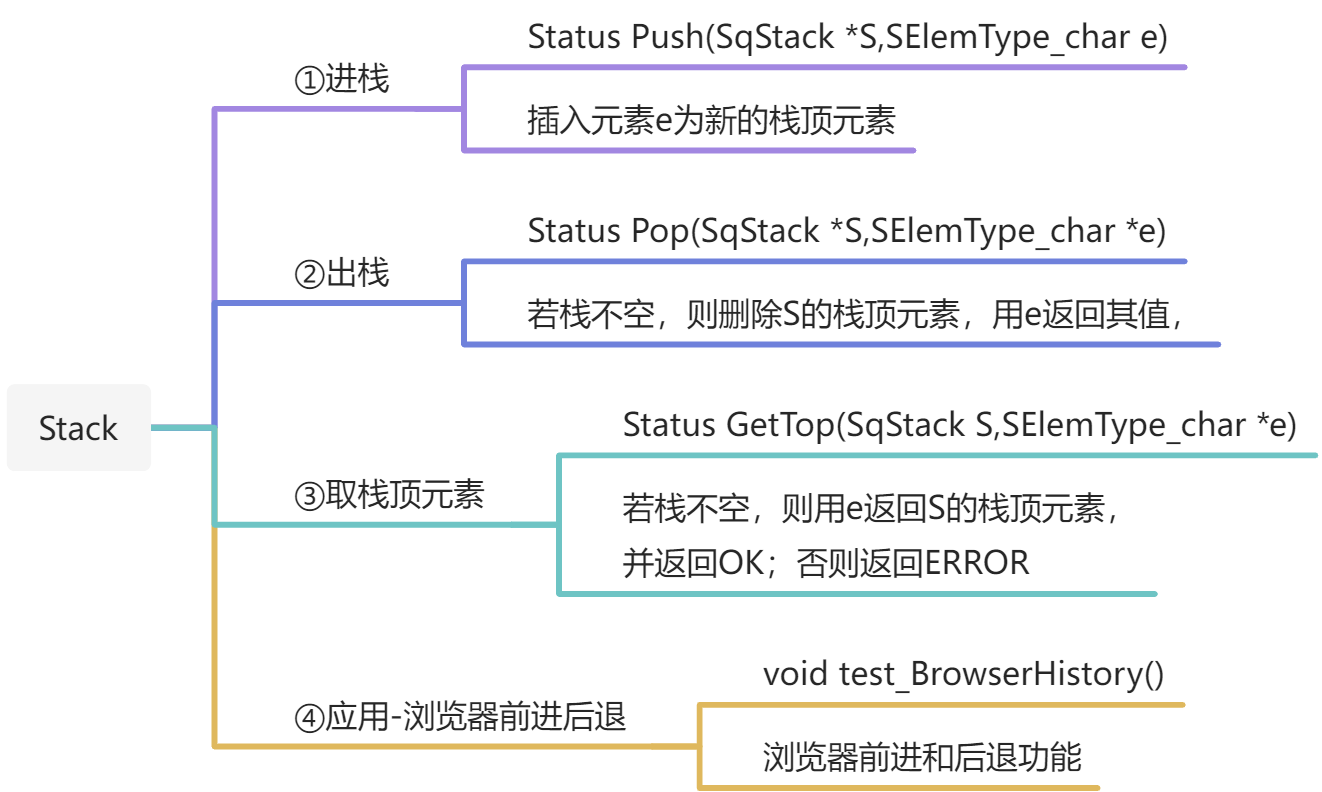
2. stack栈

/ 顺序栈结构 /
typedef struct
{
SElemType_char data[MAXSIZE];
int top; / 用于栈顶指针 /
}SqStack;

/*
①进栈
@brief
插入元素e为新的栈顶元素
@param S
@param e
@return Status
/
Status Push(SqStack S,SElemType_char e)
{
if(S->top == MAXSIZE -1) / 栈满 /
{
return ERROR;
}
S->top++;/ 栈顶指针增加一 /
S->data[S->top]=e; / 将新插入元素赋值给栈顶空间 */
// printf(“\n!!%c进栈成功!!\n”,e);
return OK;
}

/*
②出栈
@brief
若栈不空，则删除S的栈顶元素，用e返回其值，
并返回OK；否则返回ERROR
@param S
@param e
@return Status
/
Status Pop(SqStack S,SElemType_char e)
{
if(S->top==-1)
return ERROR;
e=S->data[S->top];/ 将要删除的栈顶元素赋值给e /
// printf(“\n!!%c出栈成功!!\n”,S->data[S->top]);
S->top—;/ 栈顶指针减一 /
return OK;
}

/*
③取栈顶元素
@brief Get the Top object
若栈不空，则用e返回S的栈顶元素，
并返回OK；否则返回ERROR
@param S
@param e
@return Status
/
Status GetTop(SqStack S,SElemType_char e)
{
if (S.top==-1)
return ERROR;
else
{
*e=S.data[S.top];
// printf(“\n!!%c取栈顶元素成功!!\n”,S.data[S.top]);
}
return OK;
}

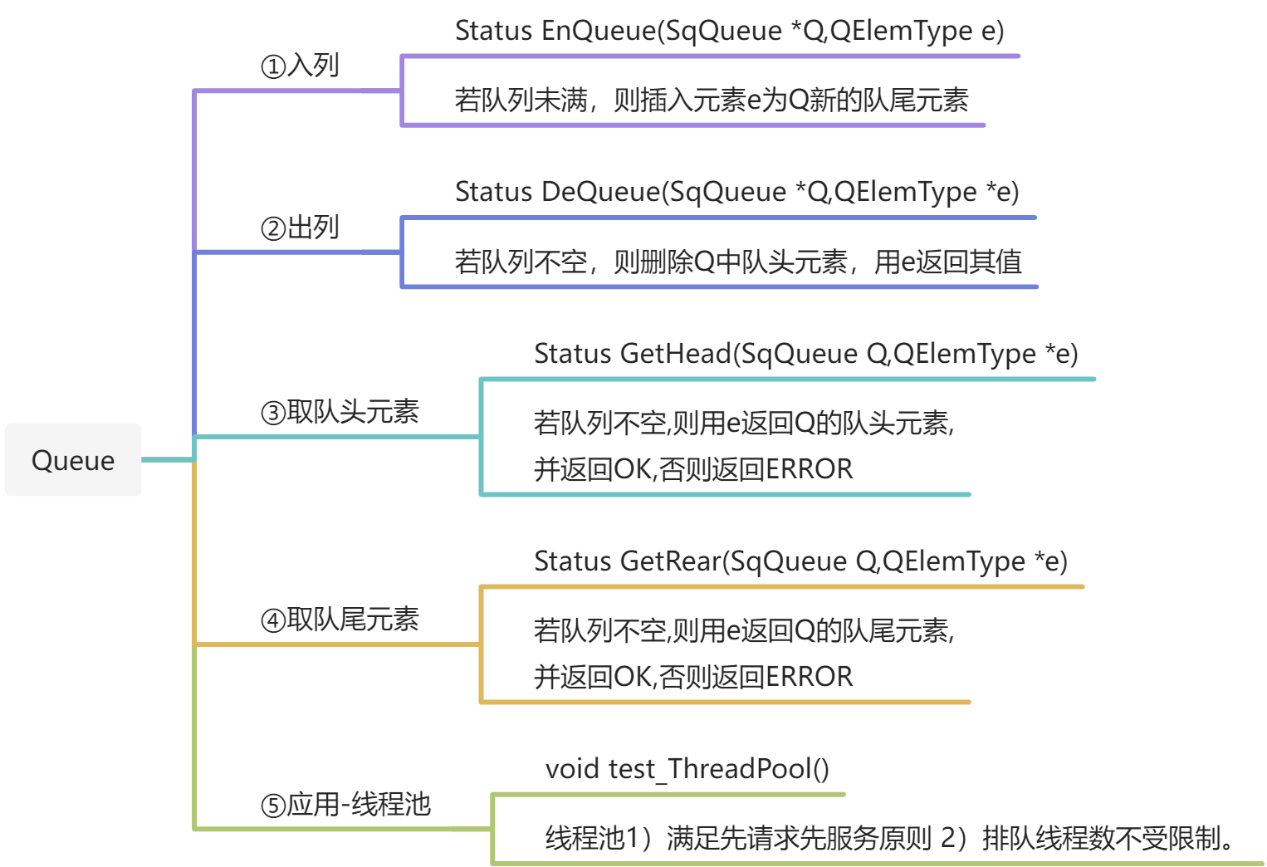
3. queue队列

/ 循环队列的顺序存储结构 /
typedef struct
{
QElemType data[MAXSIZE];
int front; / 头指针 /
int rear; / 尾指针，若队列不空，指向队列尾元素的下一个位置 /
}SqQueue;

/*
①入列
若队列未满，则插入元素e为Q新的队尾元素
@param Q
@param e
@return
/
Status EnQueue(SqQueue Q,QElemType e)
{
if ((Q->rear+1)%MAXSIZE == Q->front) / 队列满的判断 /
return ERROR;
Q->data[Q->rear]=e; / 将元素e赋值给队尾 /
Q->rear=(Q->rear+1)%MAXSIZE;/ rear指针向后移一位置， /
/ 若到最后则转到数组头部 /

// printf(“\n!!%d入列成功!!\n”,e);
return OK;
}

/*
②出列
若队列不空，则删除Q中队头元素，用e返回其值
@param Q
@param e
@return
/
Status DeQueue(SqQueue Q,QElemType e)
{
if (Q->front == Q->rear) / 队列空的判断 /
return ERROR;
e=Q->data[Q->front]; / 将队头元素赋值给e /

// printf(“\n!!%d出列成功!!\n”,*e);

Q->front=(Q->front+1)%MAXSIZE;    /* front指针向后移一位置， */<br />    /* 若到最后则转到数组头部 */<br />    return  OK;<br />}

/*
③取队头元素
若队列不空,则用e返回Q的队头元素,
并返回OK,否则返回ERROR
@param Q
@param e
@return
/
Status GetHead(SqQueue Q,QElemType e)
{
if(Q.front==Q.rear) / 队列空 /
return ERROR;
e=Q.data[Q.front];
// printf(“\n!!取队头元素%d成功!!\n”,*e);
return OK;
}

/*
④取队尾元素
若队列不空,则用e返回Q的队尾元素,
并返回OK,否则返回ERROR
@param Q
@param e
@return
/
Status GetRear(SqQueue Q,QElemType e)
{
if(Q.front==Q.rear) / 队列空 /
return ERROR;
e=Q.data[Q.rear-1];

// printf(“\n!!取队尾元素%d成功!!\n”,*e);
return OK;
}

4. bitree树

/*
@brief
递归定义
/
typedef struct BiTNode / 结点结构 /
{
SElemType_char data;/ 结点数据 /
struct BiTNode lchild,rchild; / 左右孩子指针 /
}BiTNode,*BiTree;

/*
①创建(先序)
@brief Create a Bi Tree object
以先序方式创建二叉树
@param T
@return int
/
void Create_BiTree(BiTree T)
{
//printf(“\n先序方式创建二叉树(以空格相隔)\n”);
char ch;
ch = getchar();
// scanf(“%c”,&ch);
if (ch == ‘ ‘){
T = NULL;
}else{
T = (BiTree)malloc(sizeof(BiTNode));
if (!(T)){
exit(-1);
}
(T)->data = ch; //将ch存入对应节点
Create_BiTree(&((T)->lchild));
Create_BiTree(&((T)->rchild));
}
//printf(“\n!!先序创建二叉树成功!!\n”);
}

/*
②遍历先序
@brief
初始条件: 二叉树T存在
操作结果: 先序递归遍历T
@param T
/
void PreOrderTraverse(BiTree T)
{
if(T==NULL)
return;
printf(“%c “,T->data);/ 显示结点数据，可以更改为其它对结点操作 /
PreOrderTraverse(T->lchild); / 再先序遍历左子树 /
PreOrderTraverse(T->rchild); / 最后先序遍历右子树 */
}

/*
②遍历中序
@brief
初始条件: 二叉树T存在
操作结果: 中序递归遍历T
@param T
/
void InOrderTraverse(BiTree T)
{
if(T==NULL)
return;
InOrderTraverse(T->lchild); / 中序遍历左子树 /
printf(“%c “,T->data);/ 显示结点数据，可以更改为其它对结点操作 /
InOrderTraverse(T->rchild); / 最后中序遍历右子树 */
}

/*
②遍历后序
@brief
初始条件: 二叉树T存在
操作结果: 后序递归遍历T
@param T
/
void PostOrderTraverse(BiTree T)
{
if(T==NULL)
return;
PostOrderTraverse(T->lchild); / 先后序遍历左子树 /
PostOrderTraverse(T->rchild); / 再后序遍历右子树 /
printf(“%c “,T->data);/ 显示结点数据，可以更改为其它对结点操作 */
}

/*
③求树的深度
@brief
初始条件: 二叉树T存在。
操作结果: 返回T的深度
@param T
@return int
1.如果左孩子不为空，递归左孩子
2.如果右孩子不为空，递归右孩子
/
int BiTreeDepth(BiTree T)
{
int i,j;
if(!T)
return 0;
if(T->lchild)
i=BiTreeDepth(T->lchild);
else
i=0;
if(T->rchild)
j=BiTreeDepth(T->rchild);
else
j=0;

// printf(“\n!!求树的深度成功!!\n”);
return i>j?i+1:j+1;
}

/*
④查找双亲
@brief
返回e的双亲
@param T
@param e
@return int
1.T->lchild && T->lchild->data == e，若左孩子的值==e，输出Parent：T->data
2.T->rchild && T->rchild->data == e，若右孩子的值==e，输出Parent：T->data
3.若不满足1，2两点，递归左右子树
/
int Parent(BiTree T, char e)
{
// printf(“%c”,e);
if (((T)->lchild) && ((T)->lchild->data) == e)
{
printf(“双亲节点为：%c\n”, ((T)->data));
return 1;
}else if (((T)->rchild) && ((T)->rchild->data) == e)
{
printf(“双亲节点为：%c\n”, ((T)->data));
return 1;
}
else
{
if (((T)->lchild))
{
Parent(&((T)->lchild), e);
}
if ((T)->rchild)
{
Parent(&((T)->rchild), e);
}
}
// printf(“\n!!查找双亲成功!!\n”);
return OK;
}

/*
⑤查找兄弟（左）
@brief
返回e的左兄弟
@param T
@param e
@return int
1.如果节点左孩子不为空&&节点右孩子值==e，输出节点左兄弟T->lchild->data
2.递归直到找到左孩子不为空&&节点右孩子值==e
3.如果找不到，结束（return 0）
*/
int LeftSibling(BiTree T, char e)
{
if (T->lchild && T->rchild->data == e)
{
printf(“左兄弟节点为：%c\n”, T->lchild->data);
return 1;
}
else
{
if (T->lchild)
{
LeftSibling(T->lchild, e);
}
if (T->rchild)
{
LeftSibling(T->rchild, e);
}
}
return 0;
}

/*
⑤查找兄弟（右）
@brief
返回e的右兄弟
@param T
@param e
@return int
1.如果节点右孩子不为空&&节点左孩子值==e，输出节点右兄弟T->lchild->data
2.递归直到找到右孩子不为空&&节点右孩子值==e
3.如果找不到，结束（return 0）
*/
int RightSibling(BiTree T, char e)
{
if (T->rchild && T->lchild->data == e)
{
printf(“右兄弟节点为：%c\n”, T->rchild->data);
return 1;
}
else
{
if (T->lchild)
{
RightSibling(T->lchild, e);
}
if (T->rchild)
{
RightSibling(T->rchild, e);
}
}
return 0;
}

/*
⑥查找孩子（左）
@brief
返回e的左孩子
@param T
@param e
@return int
1.如果节点值==e&&节点左孩子不为空，输出左孩子节点
2.递归直到找到节点值==e&&节点左孩子不为空
3.如果找不到，结束（return 0）
*/
int LeftChild(BiTree T, char e)
{
if (T->data == e && T->lchild)
{
printf(“左孩子节点为：%c\n”, T->lchild->data);
return 1;
}
else
{
if (T->lchild)
{
LeftChild(T->lchild, e);
}
if (T->rchild)
{
LeftChild(T->rchild, e);
}
}
return 0;
}

/*
⑥查找孩子（右）
@brief
返回e的右孩子
@param T
@param e
@return int
1.如果节点值==e&&节点右孩子不为空，输出右孩子节点
2.递归直到找到节点值==e&&节点右孩子不为空
3.如果找不到，结束（return 0）
*/
int RightChild(BiTree T, char e)
{
if (T->data == e && T->rchild)
{
printf(“右孩子节点为：%c\n”, T->rchild->data);
return 1;
}
else
{
if (T->lchild)
{
RightChild(T->lchild, e);
}
if (T->rchild)
{
RightChild(T->rchild, e);
}
}
return 0;
}

5. graph图

/*
@brief
使用邻接矩阵方式
/
typedef enum
{
DG, //构造有向图
DN, //构造有向网
UDG, //构造无向图
UDN //构造无向网
} GraphKind;

typedef struct ArcCell
{
int adj; //顶点关系类型，对无权图，用1或0表示相邻否；对带权图则为权值类型
char *info; //该弧相关信息指针
} ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];

typedef struct
{
char vers[MAX_VERTEX_NUM]; //顶点向量
AdjMatrix arcs; //邻接矩阵
int vexnum, arcnum; //图的当前顶点数vexnum和弧数arcnum
GraphKind kind; //图的种类标志
int visited1[MAX_VERTEX_NUM];
} MGraph;

/*
③定位
@brief
初始条件：图G存在，u和G中顶点有相同的特征。
操作结果：若G存在顶点u，则返回该顶点在图中的位置，否则返回其他信息。
@param G
@param v
@return int
*/
int LocateVex(MGraph G, char v)
{
int i;
for (i = 0; i < G.vexnum; i++)
{
if (v == G.vers[i])
return i;
}
exit(0); // exit(0)终止当前程序,关闭所有文件
}

/*
①创建（邻接矩阵/邻接表）
@brief
采用邻接矩阵（数组）表示法构造无向网
@param G
@return int
/
int CreateUDN(MGraph G)
{
int i, j, k, w; // w权值
char v1, v2; //顶点v1,v2

printf("请输入无向网G的顶点数：");<br />    scanf("%d", &(G->vexnum));
printf("\n请输入无向网G的弧数：");<br />    scanf("%d", &(G->arcnum));
printf("\n请输入无向网G的顶点：");<br />    fflush(stdin); //关闭一个流，并对缓冲区作处理
for (i = 0; i < G->vexnum; i++)<br />    {<br />        scanf("%c", &G->vers[i]);<br />    }
for (i = 0; i < G->vexnum; i++)<br />        for (j = 0; j < G->vexnum; j++)<br />        {<br />            G->arcs[i][j].adj = INFINITY;<br />            G->arcs[i][j].info = NULL;<br />        }<br />    for (k = 0; k < G->arcnum; k++)<br />    {<br />        printf("\n请输入无向网（顶点v1到v2有弧且权值w）<v1 v2 w>:");<br />        fflush(stdin);<br />        scanf("%c%c%d", &v1, &v2, &w);<br />        i = LocateVex(*G, v1);<br />        j = LocateVex(*G, v2);<br />        G->arcs[i][j].adj = w;<br />        G->arcs[j][i] = G->arcs[i][j];<br />    }<br />    return 1;<br />}

/*
①创建（邻接矩阵/邻接表）
@brief
采用邻接矩阵（数组）表示法构造有向图
@param G
@return int
/
int CreateDG(MGraph G)
{
int i, j, k, w; // w权值
char v1, v2; //顶点v1,v2

printf("请输入有向图G的顶点数：");<br />    scanf("%d", &G->vexnum);
printf("\n请输入有向图G的弧数：");<br />    scanf("%d", &G->arcnum);
printf("\n请输入有向图G的顶点：");<br />    fflush(stdin); //关闭一个流，并对缓冲区作处理
for (i = 0; i < G->vexnum; i++)<br />    {<br />        scanf("%c", &G->vers[i]);<br />    }
for (i = 0; i < G->vexnum; i++)<br />        for (j = 0; j < G->vexnum; j++)<br />        {<br />            G->arcs[i][j].adj = 0;<br />            G->arcs[i][j].info = NULL;<br />        }<br />    for (k = 0; k < G->arcnum; k++)<br />    {<br />        printf("\n请输入有向图（顶点v1到v2有弧且权值w）<v1 v2>:");<br />        fflush(stdin);<br />        scanf("%c%c", &v1, &v2);<br />        i = LocateVex(*G, v1);<br />        j = LocateVex(*G, v2);<br />        G->arcs[i][j].adj = 1;<br />        // G.arcs[j][i] = G.arcs[i][j];//有向图邻接矩阵不对称<br />    }<br />    return 1;<br />}

/*
①创建（邻接矩阵/邻接表）
@brief
采用邻接矩阵（数组）表示法构造有向网
@param G
@return int
/
int CreateDN(MGraph G)
{
int i, j, k, w; // w权值
char v1, v2; //顶点v1,v2

printf("请输入有向网G的顶点数：");<br />    scanf("%d", &G->vexnum);
printf("\n请输入有向网G的弧数：");<br />    scanf("%d", &G->arcnum);
printf("\n请输入有向网G的顶点：");<br />    fflush(stdin); //关闭一个流，并对缓冲区作处理
for (i = 0; i < G->vexnum; i++)<br />    {<br />        scanf("%c", &G->vers[i]);<br />    }
for (i = 0; i < G->vexnum; i++)<br />        for (j = 0; j < G->vexnum; j++)<br />        {<br />            G->arcs[i][j].adj = INFINITY;<br />            G->arcs[i][j].info = NULL;<br />        }<br />    for (k = 0; k < G->arcnum; k++)<br />    {<br />        printf("\n请输入有向网（顶点v1到v2有弧且权值w）<v1 v2 w>:");<br />        fflush(stdin);<br />        scanf("%c%c%d", &v1, &v2, &w);<br />        i = LocateVex(*G, v1);<br />        j = LocateVex(*G, v2);<br />        G->arcs[i][j].adj = w;<br />        // G.arcs[j][i] = G.arcs[i][j];//有向网邻接矩阵不对称<br />    }<br />    return 1;<br />}

/*、
①创建（邻接矩阵/邻接表）
@brief
采用邻接矩阵（数组）表示法构造无向图
@param G
@return int
/
int CreateUDG(MGraph G)
{
int i, j, k, w; // w权值
char v1, v2; //顶点v1,v2

printf("请输入无向图G的顶点数：");<br />    scanf("%d", &G->vexnum);
printf("\n请输入无向图G的弧数：");<br />    scanf("%d", &G->arcnum);
printf("\n请输入无向图G的顶点：");<br />    fflush(stdin); //关闭一个流，并对缓冲区作处理
for (i = 0; i < G->vexnum; i++)<br />    {<br />        scanf("%c", &G->vers[i]);<br />    }
for (i = 0; i < G->vexnum; i++)<br />        for (j = 0; j < G->vexnum; j++)<br />        {<br />            G->arcs[i][j].adj = INFINITY;<br />            G->arcs[i][j].info = NULL;<br />        }<br />    for (k = 0; k < G->arcnum; k++)<br />    {<br />        printf("\n请输入无向图（顶点v1到v2）<v1 v2>:");<br />        fflush(stdin);<br />        scanf("%c%c", &v1, &v2);<br />        i = LocateVex(*G, v1);<br />        j = LocateVex(*G, v2);<br />        G->arcs[i][j].adj = 1;<br />        G->arcs[j][i] = G->arcs[i][j]; //无向图邻接矩阵对称<br />    }<br />    return 1;<br />}

/*
①创建（邻接矩阵/邻接表）
@param G
@return
/
int CreateGraph(MGraph G)
{
printf(“\n请输入类型0,1,2,3;(DG(0)有向图,DN(1)有向网,UDG(2)无向图,UDN(3))无向网:\n”);
getchar();
scanf(“%d”, &G->kind);
switch (G->kind)
{
case DG:
return CreateDG(G);//采用邻接矩阵（数组）表示法构造有向图
case DN:
return CreateDN(G);//采用邻接矩阵（数组）表示法构造有向网
case UDG:
return CreateUDG(G);//采用邻接矩阵（数组）表示法构造无向图
case UDN:
return CreateUDN(G);//采用邻接矩阵（数组）表示法构造无向网
default:
return 0;
}
}

/*
④找第一个邻接点
@brief
初始条件：图G存在，v是G中的某个顶点。
操作结果：返回v的第一个邻接顶点。若顶点在G中没有邻接顶点，则返回空。
@param G
@param u
@return char
*/
char FirstadjVex(MGraph G, char u)
{
int kv, j; // kv:该顶点在图中的位置
int adj;
kv = LocateVex(G, u);
if (kv == -1)
return -1;
if (G.kind == DG || G.kind == UDG)
{
adj = 0; //图
}
else if (G.kind == DN || G.kind == UDN)
{
adj = INFINITY; //网
}
else
{
return 0;
}
for (j = 0; j < G.vexnum; j++)
{
if (G.arcs[kv][j].adj != adj)
{
// printf(“%c第一个邻接点:%c”,u,G.vers[j]);
return G.vers[j];
}
}
return 0;
}

/*
⑤找下一个邻接点
@brief
初始条件：图G存在，v是G中的某个顶点,w是v的邻接顶点。
操作结果：返回v的（相对于w的）下一个邻接顶点。若w是v的最后一个邻接顶点，则返回’空’。
@param G
@param u
@param v
@return char
/
char NextadjVex(MGraph G, char v, char w)
{
int kv, kw, j; // kv,kw:该顶点在图中的位置
int adj;
kv = LocateVex(G, v);
if (kv == -1)
return 0;
kw = LocateVex(G, w);
if (kw == -1)
{
return 0;
}

if (G.kind == DG || G.kind == UDG)<br />    {<br />        adj = 0; //图<br />    }<br />    else if (G.kind == DN || G.kind == UDN)<br />    {<br />        adj = INFINITY; //网<br />    }<br />    else<br />    {<br />        return 0;<br />    }
for (j = kw + 1; j < G.vexnum; j++)<br />    { //从w的下一个开始找邻接顶点<br />        if (G.arcs[kv][j].adj != adj)<br />        {<br />//            printf("%c的邻接顶点%c的下一个邻接顶点:%c\n",v,w,G.vers[j]);<br />            return G.vers[j];<br />        }<br />    }<br />    return 0;<br />}

Boolean visited[MAXVEX]; / 访问标志的数组 /

/*
@brief
邻接矩阵的深度优先递归算法
@param G
@param i
/
void DFS(MGraph G, int i)
{
int adj;
if (G.kind == DG || G.kind == UDG)
{
adj = 0; //图
}
else if (G.kind == DN || G.kind == UDN)
{
adj = INFINITY; //网
}
else
{
printf(“G非图,网”);
}
int j;
visited[i] = TRUE;
printf(“%c “, G.vers[i]); / 打印顶点，也可以其它操作 /
for (j = 0; j < G.vexnum; j++)
if (G.arcs[i][j].adj != adj && !visited[j])
DFS(G, j); / 对为访问的邻接顶点递归调用 /
}

/*
②遍历（深度）
@brief
初始条件：图G存在。
操作结果：对图进行深度优先遍历。在遍历过程中对每个顶点调用
函数Visit一次且仅一次。一旦Visit失败，则操作失败。
@param G
/
void DFSTraverse(MGraph G)
{
int i;
for (i = 0; i < G.vexnum; i++)
visited[i] = FALSE; / 初始所有顶点状态都是未访问过状态 /
for (i = 0; i < G.vexnum; i++)
if (!visited[i]) / 对未访问过的顶点调用DFS，若是连通图，只会执行一次 /
DFS(G, i);
}

/*
②遍历（广度）
@brief
初始条件：图G存在。
操作结果：对图进行广度优先遍历。
@param G
/
void BFSTraverse(MGraph G)
{
int i, j;
int adj;
if (G.kind == DG || G.kind == UDG)
{
adj = 0; //图
}
else if (G.kind == DN || G.kind == UDN)
{
adj = INFINITY; //网
}
else
{
printf(“G非图,网”);
}
SqQueue Q;
for (i = 0; i < G.vexnum; i++)
visited[i] = FALSE;
InitQueue(&Q); / 初始化一辅助用的队列 /
for (i = 0; i < G.vexnum; i++) / 对每一个顶点做循环 /
{
if (!visited[i]) / 若是未访问过就处理 /
{
visited[i] = TRUE; / 设置当前顶点访问过 /
visit_char(G.vers[i]); / 打印顶点，也可以其它操作 /
// printf(“%c “,G.vers[j]);
EnQueue(&Q, i); / 将此顶点入队列 /
while (!QueueEmpty(Q)) / 若当前队列不为空 /
{
DeQueue(&Q, &i); / 将队对元素出队列，赋值给i /
for (j = 0; j < G.vexnum; j++)
{
/ 判断其它顶点若与当前顶点存在边且未访问过 /
if (G.arcs[i][j].adj != adj && !visited[j])
{
visited[j] = TRUE; / 将找到的此顶点标记为已访问 /
visit_char(G.vers[j]); / 打印顶点 /
// printf(“%c “,G.vers[j]);
EnQueue(&Q, j); / 将找到的此顶点入队列 */
}
}
}
}
}
}

6. 应用

1）应用-热词
/
热门搜索关键词
/
void test_Keywords(){
int n,e,m;
List L;
KeywordsInitList(&L);
Keywords K;
do
{
printf(“\n”);
printf(“!!!!!!!!!!!!!!!!!热词!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!\n”);
printf(“！ 1 关键词请求 ———————————— ！\n”);
printf(“！ 2 热度高的关键词 | 选题3 | ！\n”);
printf(“！ 3 退出 ———————————— ！\n”);
printf(“!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!\n”);
printf(“请选择：”);
scanf(“%d”, &n);
switch (n)
{
case 1:
printf(“————关键词请求———-“);
printf(“\n”);
getchar();
scanf(“%s”,K.keywords);
printf(“\nK.keywords:%s\n”,K.keywords);
KeywordsLocateElem(L,K);
break;
case 2:
printf(“————热度高的关键词———-“);
BubbleSort(L);
printf(“\n请输入你想查的热词个数m\n”);
getchar();
/
测试
1 3
2 1
3 4
4 6
5 2

结果
第1个热词:4,热度:6
第2个热词:3,热度:4
第3个热词:1,热度:3
第4个热词:5,热度:2
第5个热词:2,热度:1
/
scanf(“%d”,&m);
KeywordsListTraverse(L,m);
break;
case 3:
break;
default:
printf(“ERROR!”);
break;
}
} while (n != 3);
}

2）应用-浏览器前进后退
/*
依次浏览了页面A、B、C后，当前页面为C。
若使用浏览器后退功能时，则可依次回到页面B和A。
当退到A之后，使用浏览器前进功能，则可以依次回到页面B和C。
但若退到B之后浏览了新页面D，则前进或后退到C都不可实现
/
void test_BrowserHistory(){
char homepage[20];
char url[20];
int steps=1;
int n,e;
do
{
printf(“\n”);
printf(“!!!!!!!!!!!!!!!!!浏览器前进和后退功能!!!!!!!!!!!!!!!!!\n”);
printf(“！ 1 浏览器首页创建 ———————————— ！\n”);
printf(“！ 2 浏览器访问新页面 | 选题2 | ！\n”);
printf(“！ 3 浏览器页面返回 | | ！\n”);
printf(“！ 4 浏览器页面前进 ———————————— ！\n”);
printf(“！ 5 关闭页面！\n”);
printf(“！ 6 退出！\n”);
printf(“!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!\n”);
printf(“请选择：”);
scanf(“%d”, &n);
switch (n)
{
case 1:
printf(“————浏览器首页创建———-“);
printf(“\n请输入浏览器首页地址(21字符内)\n”);
getchar();
scanf(“%s”,homepage);
BrowserHistory obj = browserHistoryCreate(homepage);
break;
case 2:
printf(“————浏览器访问新页面———-“);
printf(“\n请输入浏览器访问新页面(21字符内)\n”);
getchar();
scanf(“%s”,url);
browserHistoryVisit(obj, url);
break;
case 3:
printf(“————浏览器历史返回———-“);
char param_2 = browserHistoryBack(obj, steps);
printf(“\n%s<-“,param_2);
break;
case 4:
printf(“————浏览器历史前进———-“);
char * param_3 = browserHistoryForward(obj, steps);
printf(“\n->%s”,param_3);
break;
case 5:
printf(“————关闭页面———-“);
browserHistoryFree(obj);
printf(“\n关闭页面成功\n”);
break;
case 6:
break;
default:
printf(“ERROR!”);
break;
}
} while (n != 6);
}

3）应用-线程池
void test_ThreadPool(){
int n,e;
SqQueue Thread;//线程池 Thread
SqQueue CPU;//CPU
InitQueue(&Thread);//初始化
for (int i = 0; i < 16; ++i) {
EnQueue(&Thread, i);
}
InitQueue(&CPU);//初始化
for (int i = 0; i < 18; ++i) {
EnQueue(&CPU, i);
}
do
{
printf(“\n”);
printf(“!!!!!!!!!!!!!!!!!线程池!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!\n”);
printf(“！ 1 请求线程 ———————————— ！\n”);
printf(“！ 2 取出CPU进程 | 选题1 | ！\n”);
printf(“！ 3 取出线程池线程 | | ！\n”);
printf(“！ 4 查看线程池排队线程 ———————————— ！\n”);
printf(“！ 5 查看CPU运行进程！\n”);
printf(“！ 6 退出！\n”);
printf(“!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!\n”);
printf(“请选择：”);
scanf(“%d”, &n);
switch (n)
{
case 1:
printf(“————请求线程———-“);
printf(“\n请输入请求线程(数字)\n”);
getchar();
scanf(“%d”,&e);
request_thread(&Thread,&CPU,e);
break;
case 2:
printf(“————取出CPU进程———-“);
DeQueue(&CPU,&e);
printf(“\n取出CPU进程为：%d”,e);
break;
case 3:
printf(“————取出线程池线程———-“);
DeQueue(&Thread,&e);
printf(“\n取出CPU进程为：%d”,e);
break;
case 4:
printf(“————查看线程池排队线程———-“);
printf(“\n”);
QueueTraverse(Thread);
break;
case 5:
printf(“————查看CPU运行进程———-“);
printf(“\n”);
QueueTraverse(CPU);
break;
case 6:
break;
default:
printf(“ERROR!”);
break;
}
} while (n != 6);
}

4）应用-箱子装载问题的最优匹配
/*
使用平衡二叉树（AVL树），平均性能O(logn)
*/
void test_boxloading(){
int n;
char boxs[7]={‘a’,’b’,’c’,’d’,’e’,’f’,’g’};
int capacity[7]={9,10,5,5,6,8,12};
int i;
int j,e;
BiTree1 T=NULL;
Status taller;
int weight;
do
{
printf(“\n”);
printf(“!!!!!!!!!!!!!!!!!箱子装载问题!!!!!!!!!!!!!!!!!!!!!!!!\n”);
printf(“！ 1 初始化箱子 ———————————— ！\n”);
printf(“！ 2 寻找最佳箱子 | 选题5 | ！\n”);
printf(“！ 3 退出 ———————————— ！\n”);
printf(“!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!\n”);
printf(“请选择：”);
scanf(“%d”, &n);
switch (n)
{
case 1:
printf(“————初始化箱子———-“);
for(i=0;i<7;i++)
{
InsertAVL(&T,capacity[i],&taller);
}
printf(“\n初始化箱子成功\n”);
break;
case 2:
printf(“————寻找最佳箱子———-“);
printf(“\n请输入物品重量：”);
scanf(“%d”,&weight);
InOrder(T,weight,&e);
// printf(“\n容量:%d\n”,e);
for (j = 0; j < 7; ++j) {
if(e==capacity[j]){
break;
}
}
printf(“\n最佳箱子%c,容量:%d\n”,boxs[j],e);
break;
case 3:
break;
default:
printf(“ERROR!”);
break;
}
} while (n != 3);
}

5）应用-三度好友
/
应用-三度好友
/
void test_friend(){
int n;
MGraph G;
// G.kind = UDN;
char node;
do
{
printf(“\n”);
printf(“!!!!!!!!!!!!!!!!!应用-三度好友!!!!!!!!!!!!!!!!\n”);
printf(“！ 1 创建关系 ——————————— ！\n”);
printf(“！ 2 找到指定用户的三度好友 | 选题4 | ！\n”);
printf(“！ 3 退出 ——————————— ！\n”);
printf(“!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!\n”);
printf(“请选择：”);
scanf(“%d”, &n);
switch (n)
{
case 1:
printf(“————创建关系———-“);
/
@brief
测试用网
a
/ | \ \
b e c i
/ \ \ \
h d g f
/ \ \
j k l
顶点数：12
弧数：11
顶点：abcdefghijkl
有向图：ab,ae,ac,ai,bd,bh,eg,cf,hj,dk,gl

/
/**
@brief
测试用网
a
/ | \ \
b e c i
/ \ \ \
h d g f
/ \ \ \
j k l s
顶点数：13
弧数：12
顶点：abcdefghijkls
有向图：ab,ae,ac,ai,bd,bh,eg,cf,hj,dk,gl,fs

/
printf(“\n”);
getchar();
CreateUDN(&G);
PrintMatrix(G);
break;
case 2:
printf(“————找到找到指定用户的三度好友的三度好友———-“);
printf(“\n指定用户\n”);
getchar();
scanf(“%c”,&node);
GetThreeDegree(&G,node);
break;
case 3:
break;
default:
printf(“ERROR!”);
break;
}
} while (n != 3);
}

四.测试与结论

1. linklist链表

① 创建
物联12002-翁修林-202004071-18(数据结构课设) - 图8
② 插入

③ 删除

④ 查找

⑤ 应用-热词
测试
热词热度
1 3
2 1
3 4
4 6
* 5 2

2. stack栈

① 进栈
物联12002-翁修林-202004071-18(数据结构课设) - 图14
② 出栈

③ 取栈顶元素

④ 应用-浏览器前进后退

3. queue队列

① 入列
物联12002-翁修林-202004071-18(数据结构课设) - 图26
② 出列

③ 取队头元素

④ 取队尾元素

⑤ 应用-线程池
测试：线程池Thread已有0~15的16个线程，CPU有0~17的18个线程。

4. bitree树

① 创建
/*
@brief
二叉树如下
a
/ \
b c
/ \
d e

abd e c
*/
物联12002-翁修林-202004071-18(数据结构课设) - 图36
② 遍历（先序、中序、后序）

③ 求树的深度

④ 查找双亲

⑤ 查找兄弟（左/右）

⑥ 查找孩子（左/右）

⑦ 应用-箱子装载问题的最优匹配
箱子a，b，c，d，e，f，g
容量9，10，5，6，4，8，12
物联12002-翁修林-202004071-18(数据结构课设) - 图42

5. graph图

① 创建（邻接矩阵/邻接表）
/*
@brief
测试用网
a
/ | \
b \ c
\ \ /
d —— e
顶点数：5
弧数：6
顶点：abcde
有向图：ab,ac,ae,bd,de,ec
*/
物联12002-翁修林-202004071-18(数据结构课设) - 图44
② 遍历（深度/广度）

③ 定位

④ 找第一个邻接点

⑤ 找下一个邻接点

⑥ 应用-三度好友

五.难点与收获

难点

1.在做那5个选题时，对其存储类型的选择。例如应用-箱子装载问题的最优匹配用平衡二叉树。
2.各种存储结构函数的复用性还不是太完美。
3.对存储结构函数的一些细节不是十分熟练。

收获

1.发现一些自己平常时的问题，顺便也算是复习了一下。
2.锻炼了自己的排错能力，和独自思考。

指导老师意见：

成绩: 教师签名：

年月日