第二章 导数与微分
导数和微分是高等数学中的重要内容之一,也是今后讨论一切问题的基础。它从根本上反映了函数的变化情况,我们将陆续介绍倒数和微分的用途。
§2、1 导数的概念
一、 引例
1、 线问题:切线的概念在中学已见过。从几何上看,在某点的切线就是一直线,它在该点和曲线相切。准确地说,曲线在其上某点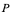 的切线是割线
的切线是割线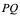 当
当 沿该曲线无限地接近于
沿该曲线无限地接近于 点的极限位置。
点的极限位置。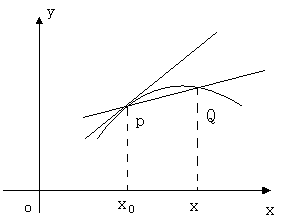
设曲线方程为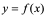 ,设
,设 点的坐标为
点的坐标为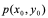 ,动点
,动点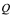 的坐标为
的坐标为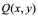 ,要求出曲线在
,要求出曲线在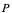 点的切线,只须求出
点的切线,只须求出 点切线的斜率
点切线的斜率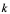 。由上知,
。由上知,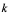 恰好为割线
恰好为割线 的斜率的极限。我们不难求得
的斜率的极限。我们不难求得 的斜率为:
的斜率为: ;因此,当
;因此,当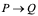 时,其极限存在的话,其值就是
时,其极限存在的话,其值就是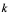 ,即
,即 。
。
若设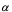 为切线的倾角,则有
为切线的倾角,则有 。
。
2、速度问题:设在直线上运动的一质点的位置方程为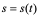 (
(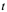 表示时刻),又设当
表示时刻),又设当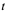 为
为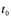 时刻时,位置在
时刻时,位置在 处,问:质点在
处,问:质点在 时刻的瞬时速度是多少?
时刻的瞬时速度是多少?
为此,可取 近邻的时刻
近邻的时刻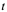 ,
,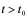 ,也可取
,也可取 ,在由
,在由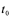 到
到 这一段时间内,质点的平均速度为
这一段时间内,质点的平均速度为 ,显然当
,显然当 与
与 越近,用
越近,用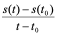 代替
代替 的瞬时速度的效果越佳,特别地,当
的瞬时速度的效果越佳,特别地,当 时,
时,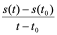
 某常值
某常值 ,那么
,那么 必为
必为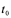 点的瞬时速度,此时,
点的瞬时速度,此时,

3、同理可讨论质量非均匀分布的细杆的线密度问题,设细杆分布在 上的质量
上的质量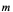 是
是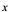 的函数
的函数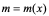 ,那么在
,那么在 处的线密度为
处的线密度为

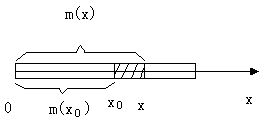
二、 导数的定义
综合上几个问题,它们均归纳为这一极限 (其中
(其中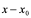 为自变量
为自变量 在
在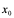 的增量,
的增量, 为相应的因变量的增量),若该极限存在,它就是所要讲的导数。
为相应的因变量的增量),若该极限存在,它就是所要讲的导数。
定义:设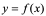 在
在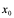 点的某邻域内有定义,且当自变量在
点的某邻域内有定义,且当自变量在 点有一增量
点有一增量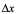 (
(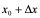 仍在该邻域中)时,函数相应地有增量
仍在该邻域中)时,函数相应地有增量 ,若增量比极限:
,若增量比极限: 即
即 存在,就称其值为
存在,就称其值为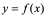 在
在 点的导数,记为
点的导数,记为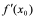 ,
, ,
, 或
或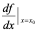 。
。
即 等等,这时,也称
等等,这时,也称 在
在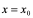 点可导或有导数,导数存在。
点可导或有导数,导数存在。
注 1:导数的常见形式还有: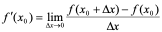 ;
;
 ;
;
 ;
;
2: 反映的是曲线在
反映的是曲线在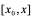 上的平均变化率,而
上的平均变化率,而 是在点
是在点 的变化率,它反映了函数
的变化率,它反映了函数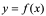 随
随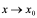 而变化的快慢程度。
而变化的快慢程度。
3:这里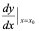 与
与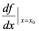 中的
中的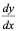 与
与 是一个整体记号,而不能视为分子
是一个整体记号,而不能视为分子 或
或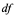 与分母
与分母 ,待到后面再讨论。
,待到后面再讨论。
4:若极限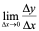 即
即 不存在,就称
不存在,就称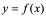 在
在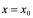 点不可导。特别地,若
点不可导。特别地,若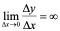 ,也可称
,也可称 在
在 的导数为
的导数为 ,因为此时
,因为此时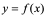 在
在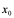 点的切线存在,它是垂直于
点的切线存在,它是垂直于 轴的直线
轴的直线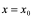 。
。
若 在开区间
在开区间 内的每一点处均可导,就称
内的每一点处均可导,就称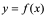 在
在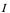 内可导,且对
内可导,且对 ,均有一导数值
,均有一导数值 ,这时就构造了一新的函数,称之为
,这时就构造了一新的函数,称之为 在
在 内的导函数,记为
内的导函数,记为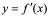 ,或
,或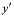 ,
, ,
, 等。
等。
事实上,  或
或
注 5:上两式中, 为
为 内的某一点,一旦选定,在极限过程中就为不变,而
内的某一点,一旦选定,在极限过程中就为不变,而 与
与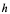 是变量。但在导函数中,
是变量。但在导函数中, 是变量。
是变量。
6: 在
在 的导数
的导数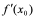 就是导函数
就是导函数 在
在 点的值,不要认为是
点的值,不要认为是 ;
;
7:为方便起见,导函数就称为导数,而 是在
是在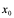 点的导数。
点的导数。
【例1】 设 ,证明欲
,证明欲 ,那么
,那么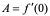 。
。
证明:因为
所以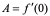 。
。
【例2】 若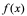 在
在 点可导,问:
点可导,问: ?
?
解: 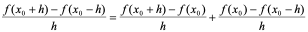
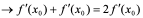 。
。
反过来,亦证明: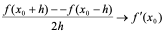 。
。
三、 求导数举例
【例3】 求函数 (
( 为常数)的导数。
为常数)的导数。
解:在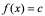 中,不论
中,不论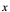 取何值,起其函数值总为
取何值,起其函数值总为 ,所以,对应于自变量的增量
,所以,对应于自变量的增量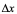 ,有
,有
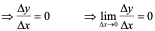 ,即
,即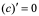 。
。
注:这里是指 在任一点的导数均为0,即导函数为0。
在任一点的导数均为0,即导函数为0。
【例4】 求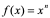 (
( 为正整数)在
为正整数)在 点的导数。
点的导数。
解: 即
即 ,
,
亦即 ,若将
,若将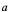 视为任一点,并用
视为任一点,并用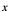 代换,即得
代换,即得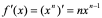
注:更一般地,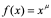 (
( 为常数)的导数为
为常数)的导数为 ,由此可见,
,由此可见,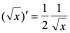 ,
,  。
。
【例5】 求 在
在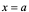 点的导数。
点的导数。
解:  ,即
,即
同理:若视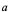 为任意值,并用
为任意值,并用 代换,使得
代换,使得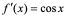 ,即
,即 。
。
注:同理可证: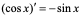 。
。
【例6】 求 的导数。
的导数。
解: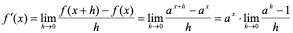
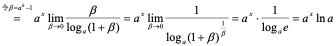
所以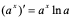 。
。
注:特别地, 。
。
【例7】 求 的导数。
的导数。
解: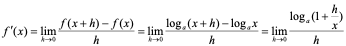
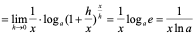 。
。
注 1:等最后讲到反函数求导时,可将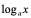 作为
作为 的反函数来求导;
的反函数来求导;
2:一般地说,求导有四步:
一、给出 ;
;
二、算出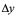 ;
;
三、求增量比 ;
;
四、求极限。
3、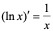 。
。
【例8】 讨论 在
在 处的导数。
处的导数。
解:考虑 ,由§1.4例4知
,由§1.4例4知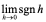 不存在,故
不存在,故 在
在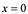 点不可导。
点不可导。
然而,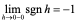 及
及 ,这就提出了一个单侧导数的问题,一般地,若
,这就提出了一个单侧导数的问题,一般地,若 ,即
,即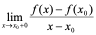 [
[ 即
即
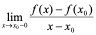 ]存在,就称其值为
]存在,就称其值为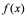 在
在 点的右(左)导数,并记为
点的右(左)导数,并记为 ,即
,即
[ ]。
]。
定理1: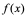 在
在 点可导
点可导
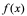 在
在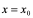 点的左导数和右导数均存在,且相等,即
点的左导数和右导数均存在,且相等,即
 。
。
注1:[例8] 的左导数为-1,右导数为1。因为
的左导数为-1,右导数为1。因为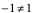 ,所以在
,所以在 点不可导;
点不可导;
2:[例8]也说明左可导又右可导,也不能保证可导;
3:左、右导数统称为单侧导数;
4:若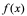 在
在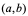 内可导,且在
内可导,且在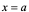 点右可导,在
点右可导,在 点左可导,即
点左可导,即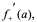
 存在,就称
存在,就称 在
在 上可导。
上可导。
四、 导数的几何意义
由前面的讨论知::函数 在
在 的导数
的导数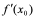 就是该曲线在
就是该曲线在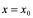 点处的切线斜率
点处的切线斜率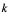 ,即
,即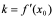 ,或
,或 为切线的倾角。从而,得切线方程为
为切线的倾角。从而,得切线方程为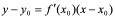 。若
。若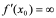 ,
,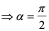 或
或
 切线方程为:
切线方程为: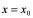 。过切点
。过切点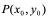 ,且与
,且与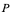 点切线垂直的直线称为
点切线垂直的直线称为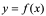 在
在 点的法线。如果
点的法线。如果
 ,法线的斜率为
,法线的斜率为 ,此时,法线的方程为:
,此时,法线的方程为: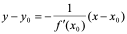 。
。
如果 =0,法线方程为
=0,法线方程为 。
。
【例9】 求曲线 在点
在点 处的切线与法线方程。
处的切线与法线方程。
解:由于 ,所以
,所以 在
在 处的切线方程为:
处的切线方程为:
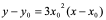
当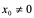 时,法线方程为:
时,法线方程为: 
当 时,法线方程为:
时,法线方程为: 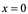 。
。
五、 函数的可导性与连续性之间的关系
定理2:如果函数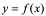 在
在 点可导,那么在该点必连续。
点可导,那么在该点必连续。
证明:由条件知: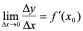 是存在的,其中
是存在的,其中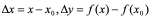 ,
,
由§1、5定理1(i) (
( 为无穷小)
为无穷小)
显然当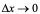 时,有
时,有 ,所以由§1、9定义1",即得函数
,所以由§1、9定义1",即得函数 在
在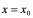 点连续,证毕。
点连续,证毕。
注 1:本定理的逆定理不成立,即连续未必可导。
反例: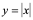 在
在 点连续,但不可导。
点连续,但不可导。
【例10】 求常数 使得
使得 在
在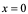 点可导。
点可导。
解:若使 在
在 点可导,必使之连续,故
点可导,必使之连续,故
 。
。
又若使 在
在 点可导,必使之左右导数存在,且相等,由函数知,左右导数是存在的,且
点可导,必使之左右导数存在,且相等,由函数知,左右导数是存在的,且


所以若有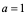 ,则
,则 ,此时
,此时 在
在 点可导,所以所求常数为
点可导,所以所求常数为
 。
。
§2、2 函数的和、差、积、商的求导法则
定理 1:若函数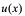 和
和 在点
在点 都可导,则
都可导,则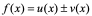 在
在 点也可导,且
点也可导,且
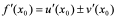 。
。
证明: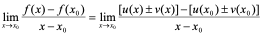
= =
=
所以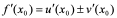 。
。
注 1:本定理可推广到有限个可导函数上去。
2:本定理的结论也常简记为 。
。
定理2:若 和
和 在
在 点可导,则
点可导,则 在
在 点可导,且有
点可导,且有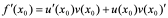 。
。
证明:
=
=
=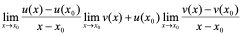
=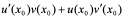
即  。
。
注 1:若取 为常数,则有:
为常数,则有: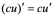 ;
;
2:本定理可推广到有限个可导函数的乘积上去,例如:
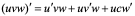
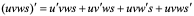 等。
等。
定理3:若 都在
都在 点可导,且
点可导,且 ,则
,则 在
在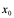 点也可导,且
点也可导,且 。
。
证明:
=
=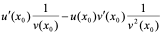
=
即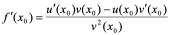
注1:本定理也可通过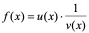 ,及
,及 的求导公式来得;
的求导公式来得;
2:本公式简化为 ;
;
3:以上定理1~3中的 ,若视为任意,并用
,若视为任意,并用 代替,使得函数的和、差、积、商的求导函数公式。
代替,使得函数的和、差、积、商的求导函数公式。
【例1】 设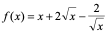 ,求
,求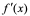 。
。
解: 
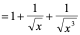 。
。
【例2】 设 ,求
,求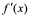 。
。
解: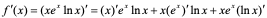

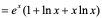 。
。
【例3】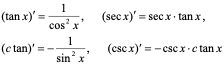
§2.3 反函数的导数、复合函数的求导法则
一、反函数的导数
定理1:设 为
为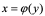 的反函数,若
的反函数,若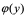 在
在 的某邻域内连续,严格单调,且
的某邻域内连续,严格单调,且 ,则
,则 在
在 (即
(即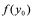 点有导数),且
点有导数),且 。
。
证明:

所以 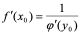 。
。
注1: ,因为
,因为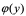 在
在 点附近连续,严格单调;
点附近连续,严格单调;
2:若视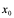 为任意,并用
为任意,并用 代替,使得
代替,使得 或
或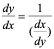 ,其中
,其中 均为整体记号,各代表不同的意义;
均为整体记号,各代表不同的意义;
3: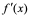 和
和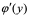 的“′”均表示求导,但意义不同;
的“′”均表示求导,但意义不同;
4:定理1即说:反函数的导数等于直接函数导数的倒数;
5:注意区别反函数的导数与商的导数公式。
【例1】 求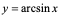 的导数,
的导数,
解:由于 ,是
,是 的反函数,由定理1得:
的反函数,由定理1得: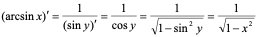 。
。
注1:同理可证: ;
;
2: 。
。
【例2】 求 的导数
的导数 。
。
解:利用指数函数的导数,自己做。
二复合函数的求导公式
复合函数的求导问题是最最常见的问题,对一复合函数往往有这二个问题:1.是否可导?2.即使可导,导数如何求?复合函数的求导公式解决的就是这个问题。
定理2(复合函数求导法则):如果 在
在 点可导,且
点可导,且 在
在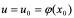 点也可导,那么,以
点也可导,那么,以 为外函数,以
为外函数,以 为内函数,所复合的复合函数
为内函数,所复合的复合函数 在
在 点可导,且
点可导,且 ,或
,或
证明: 
=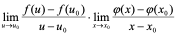 =
=
所以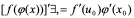 。
。
注 1:若视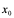 为任意,并用
为任意,并用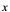 代替,便得导函数:
代替,便得导函数:
 ,或
,或
或 。
。
2: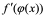 与
与 不同,前者是对变量
不同,前者是对变量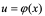 求导,后者是对变量
求导,后者是对变量 求导,注意区别。
求导,注意区别。
3:注意区别复合函数的求导与函数乘积的求导。
4:复合函数求导可推广到有限个函数复合的复合函数上去,如:
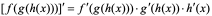 等。
等。
【例3】 求 的导数。
的导数。
解: 可看成
可看成 与
与 复合而成,
复合而成, ,
,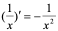 ,
,  。
。
【例4】 求 (
( 为常数)的导数。
为常数)的导数。
解: 是
是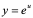 ,
, 复合而成的。
复合而成的。
所以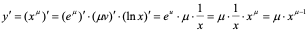 。
。
这就验证了前面§2、1的[例4]。
由此可见,初等函数的求导数必须熟悉(i)基本初等函数的求导;(ii)复合函数的分解;(iii)复合函数的求导公式;只有这样才能做到准确。在解题时,若对复合函数的分解非常熟悉,可不必写出中间变量,而直接写出结果。
【例5】 ,求
,求 。
。
解: 。
。
【例6】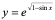 ,求
,求 。
。
解: 
 。
。
【例7】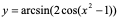 ,求
,求 。
。
解:
=
=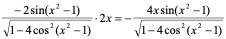 。
。
【例8】 ,求
,求 。
。
解:
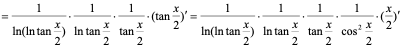
 。
。
【例9】
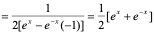 ,
,
即 。同理,
。同理, 。
。
【例10】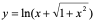 ,求
,求 。
。
解:

 。
。
同理: 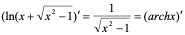 。
。
§2、4 初等函数的求导公式
1、常数和基本初等函数的求导公式:
(1) (2)
(2)
(3) (4)
(4)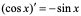
(5) (6)
(6)
(7) (8)
(8)
(9)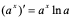 (10)
(10)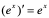
(11) (12)
(12)
(13) (14)
(14)
(15) (16)
(16)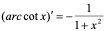
(17)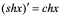 (18)
(18)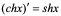
(19)
(20)
(21)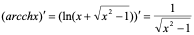
(22)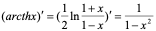
2、函数的四则运算的求导法则:
设 ,则
,则
(i)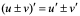 (ii)
(ii)
(iii) (iv)
(iv)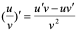
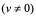
3、复合函数的求导法则:
设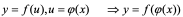 的导数为:
的导数为:  或
或 或
或 
§ 2.5 高阶导数
前面讲过,若质点的运动方程 ,则物体的运动速度为
,则物体的运动速度为 ,或
,或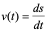 ,而加速度
,而加速度 是速度
是速度 对时间
对时间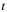 的变化率,即
的变化率,即 是速度
是速度 对时间
对时间 的导数:
的导数: 或
或 ,由上可见,加速度
,由上可见,加速度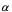 是
是 的导函数的导数,这样就产生了高阶导数,一般地,先给出下列定义:
的导函数的导数,这样就产生了高阶导数,一般地,先给出下列定义:
定义:若函数 的导函数
的导函数 在
在 点可导,就称
点可导,就称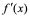 在点
在点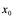 的导数为函数
的导数为函数 在点
在点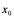 处的二阶导数,记为
处的二阶导数,记为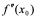 ,即
,即 ,此时,也称函数
,此时,也称函数 在点
在点 处二阶可导。
处二阶可导。
注1:若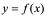 在区间
在区间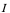 上的每一点都二次可导,则称
上的每一点都二次可导,则称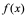 在区间
在区间 上二次可导,并称
上二次可导,并称 为
为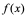 在
在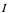 上的二阶导函数,简称二阶导数;
上的二阶导函数,简称二阶导数;
2:仿上定义,由二阶导数 可定义三阶导数
可定义三阶导数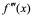 ,由三阶导数
,由三阶导数 可定义四阶导数
可定义四阶导数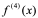 ,一般地,可由
,一般地,可由 阶导数
阶导数 定义
定义 阶导数
阶导数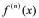 ;
;
3:二阶以上的导数称为高阶导数,高阶导数与高阶导函数分别记为: ,
,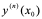 ,
,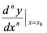 或
或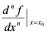 与
与 或
或 ;
;
4:开始所述的加速度就是 对
对 的二阶导数,依上记法,可记
的二阶导数,依上记法,可记 或
或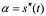 ;
;
5:未必任何函数所有高阶都存在;
6:由定义不难知道,对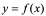 ,其导数(也称为一阶导数)的导数为二阶导数,二阶导数的导数为三阶导数,三阶导数的导数为四阶导数,一般地,
,其导数(也称为一阶导数)的导数为二阶导数,二阶导数的导数为三阶导数,三阶导数的导数为四阶导数,一般地,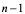 阶导数的导数为
阶导数的导数为 阶导数,否则,因此,求高阶导数是一个逐次向上求导的过程,无须其它新方法,只用前面的求导方法就可以了。
阶导数,否则,因此,求高阶导数是一个逐次向上求导的过程,无须其它新方法,只用前面的求导方法就可以了。
【例1】 ,求
,求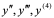 。
。
解: 。
。
【例2】 ,求各阶导数。
,求各阶导数。
解: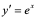 ,
,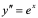 ,
, ,
, ,显然易见,对任何
,显然易见,对任何 ,有
,有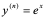 ,
,
即 。
。
【例3】 ,求各阶导数。
,求各阶导数。
解:



……
一般地,有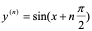 ,即
,即 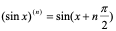 。
。
同样可求得 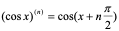 。
。
【例4】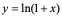 ,求各阶导数。
,求各阶导数。
解: ,
,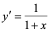 ,
, ,
, ,
,
 ,……
,……
一般地,有 
即 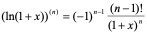 。
。
【例5】 ,
, 为任意常数,求各阶导数。
为任意常数,求各阶导数。
解: ,
,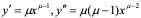 ,
, ,
,
 ,
,
一般地, 
即  。
。
(i) 当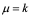 为正整数时,
为正整数时,
a) 时,
时,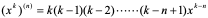 ;
;
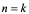 时,
时,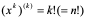 ;
;
 时,
时, ;
;
(ii)当 为正整数时,必存在一自然数
为正整数时,必存在一自然数 ,使得当
,使得当 ,
, 在
在 处不存在。
处不存在。
如: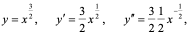 然而,
然而,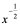 在
在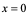 处是无意义,即说明
处是无意义,即说明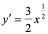 在
在 处无导数,或
处无导数,或 在
在 处不存在。
处不存在。
【例6】 ,求
,求 。
。
解:  ,
,
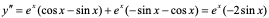 ,
,
 。
。
注:高阶导数有如下运算法则:
(1) ,
,
(2) ,
,
……,
+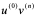 。其中
。其中 。 Leibinz公式
。 Leibinz公式
【例7】上例中,求 。
。
解: 

=
=
=
=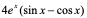 。
。
【例8】验证 满足关系式:
满足关系式: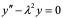 (其中
(其中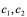 为任意常数)。
为任意常数)。
解:
所以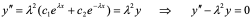 。
。
【例9】验证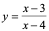 满足关系式:
满足关系式: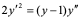 。
。
解:
又
所以 。
。
§2、6 隐函数的导数、由参数方程所确定的函数的导数
一、隐函数的导数
以前,我们所接触的函数,其因变量大多是由其自变量的某个算式来表示的,比如: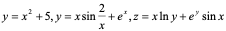 等等,象这样一类的函数称为显函数。
等等,象这样一类的函数称为显函数。
但在实际问题中,函数并不全是如此,设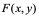 是定义在区域
是定义在区域 上的二元函数,若存在一个区域
上的二元函数,若存在一个区域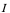 ,对于
,对于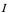 中的每一个
中的每一个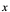 的值,恒有区间
的值,恒有区间 上唯一的一个值
上唯一的一个值 ,使之与
,使之与 一起满足方程:
一起满足方程: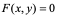 ……(1)
……(1)
就称方程(1)确定了一个定义域为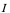 ,值域含于
,值域含于 中的函数,这个函数就称为由方程(1)所确定的隐函数,若将它记为
中的函数,这个函数就称为由方程(1)所确定的隐函数,若将它记为 ,则有:在
,则有:在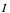 上,
上, 。
。
【例1】 确定了隐函数:
确定了隐函数: 。
。
【例2】 能确定出定义在
能确定出定义在 上的函数值不小于0的隐函数
上的函数值不小于0的隐函数 ,也能确定出定义在
,也能确定出定义在 上的函数值不大于0的隐函数
上的函数值不大于0的隐函数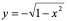 。
。
上面求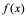 的过程是将一个隐函数转化为显函数,也称为隐函数的显化。
的过程是将一个隐函数转化为显函数,也称为隐函数的显化。
注 1:在不产生误解的情况下,其取值范围可不必一一指明;
2:并不是任一方程(1)都能确定出隐函数,比如: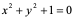 ,不可能找到
,不可能找到 ,使得
,使得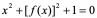 ;
;
3:即使方程(1)能确定一个隐函数,但未必能象上二例一样从方程中解出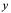 ,如:
,如: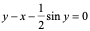 ,我们可证明它确实能确定一个隐函数,但无法表示成
,我们可证明它确实能确定一个隐函数,但无法表示成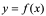 的形式,即不能显化。
的形式,即不能显化。
实际问题中,有时需要计算隐函数的导数,如果隐函数可显化,则求导没什么问题,同前一样,若隐函数不能显化,我们就直接从(1)算出其隐函数的导数。(以后我们还将介绍更一般的方法)。
【例3】 ,求
,求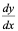 。
。
解:在方程的两边同时对 求导,得
求导,得
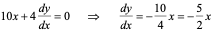 。
。

