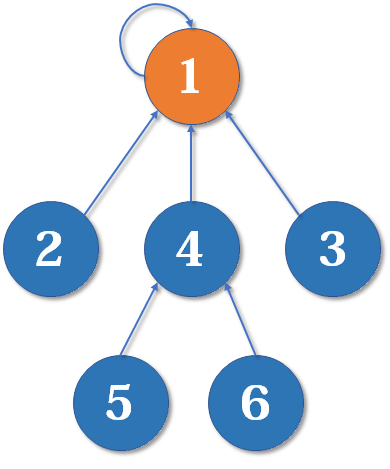
基础知识

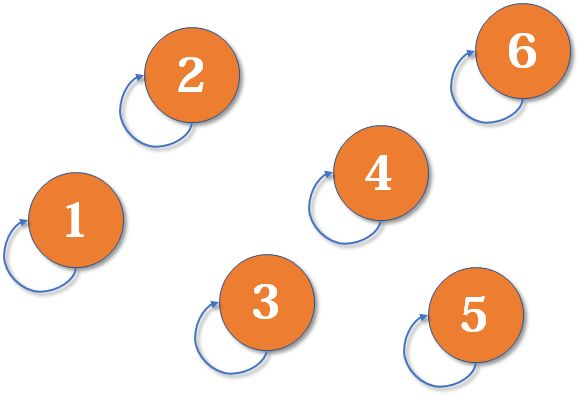
image.png

  • 经过合并最终可得到1为1 2 3的父节点，4为4 5 6的父节点

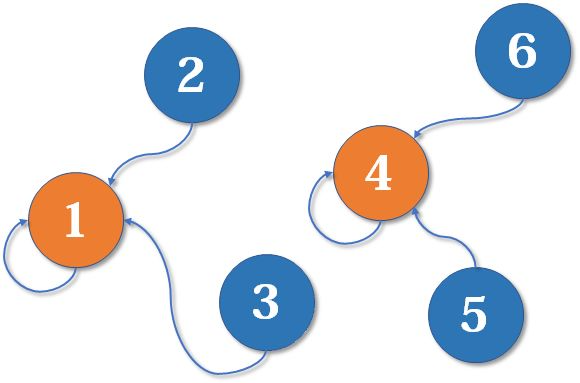
image.png

  • 再经过合并，1战胜4，所有子集的父节点都是1，就可以看成一棵树

image.png

初始化

  • 初始化时，每个节点的父节点都是自己

    1. int fa[MAXN];
    2. void init(int n)
    3. {
    4.   for (int i = 1; i <= n; ++i)
    5.       fa[i] = i;
    6. }

    查询

  • 递归查询两个子节点是否为同一集合，就看他们父节点是否相同：一层一层访问父节点，直至根节点（根节点的标志就是父节点是本身）。要判断两个元素是否属于同一个集合，只需看它们的根节点是否相同。

    1. int find(int x)
    2. {
    3.   if(fa[x] == x)
    4.       return x;
    5.   else
    6.       return find(fa[x]);
    7. }

    合并

  • 将两个节点的根节点设为一样，一般是让前一个节点的根节点设置为后一个节点的根节点

    1. void merge(int i, int j)
    2. {
    3.   fa[find(i)] = find(j);
    4. }

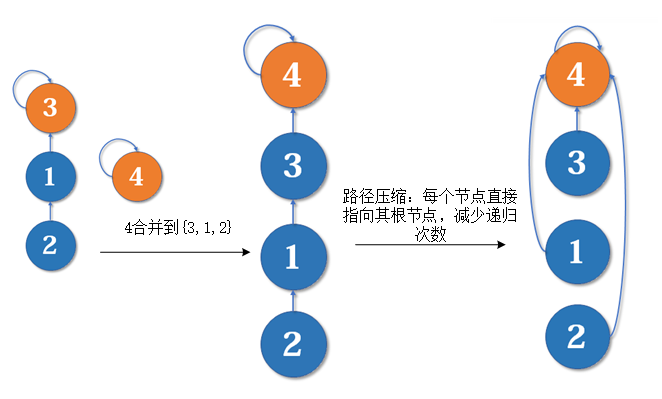
    路径压缩

  • 每次合并时，如果按照原始操作，很可能会形成链表，链表结构的查询效率比树的效率要低。

  • 路径压缩：合并时，让每个节点的父节点设置为根节点，减少递归次数。初始化过程与原始并查集一样。

image.png

查询合并

  1. int find(int x)
  2. {
  3.     if(x == fa[x])
  4.         return x;
  5.     else{
  6.         fa[x] = find(fa[x]);  //父节点设为根节点
  7.         return fa[x];         //返回父节点
  8.     }
  9.     // 也可以写为
  10.     return x == fa[x] ? x : (fa[x] = find(fa[x]));
  11. }

按秩合并

  • 路径压缩的情况下，虽然降低了查询复杂度，但是节点多的树形结构中，由于路径压缩只在查询时进行，也只压缩一条路径，所以并查集最终的结构仍然可能是比较复杂的，进而采用按秩合并。
  • 原理：简单的树往复杂的树上合并，到根节点距离变长的节点个数比较少，尽可能不增树深度。

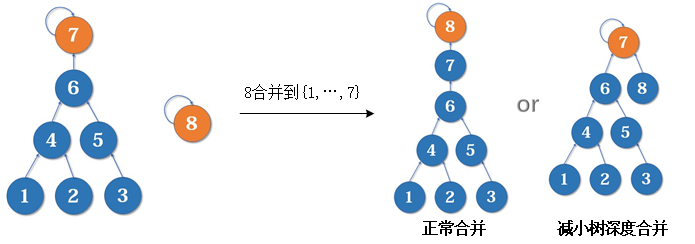
image.png

  • 具体流程

    1. 数组rank[]记录每个根节点对应的树的深度（如果不是根节点，其rank相当于以它作为根节点的子树的深度）。

    2. 一开始，把所有元素的rank（秩）设为1。

      1. void init(int n)
      2. {
      3. for (int i = 1; i <= n; ++i)
      4. {
      5.   fa[i] = i;
      6.   rank[i] = 1;
      7. }
      8. }

    3. 查询过程与路径压缩的查询合并一致

    4. 合并时比较两个根节点，把rank较小者往较大者上合并，如果深度相同且根节点不同，则新的根节点的深度+1，下次再调用时就会把两个节点集合合并在一起
      1. void merge(int i, int j)
      2. {
      3. int x = find(i), y = find(j);    //先找到两个根节点
      4. if (rank[x] <= rank[y])
      5.   fa[x] = y;
      6. else
      7.   fa[y] = x;
      8. if (rank[x] == rank[y] && x != y)
      9.   rank[y]++;                   //如果深度相同且根节点不同，则新的根节点的深度+1
      10. }
      image.png