大O符号

引入：背包问题
组合优化的问题，问题可以描述为：给定一定的物品，每种物品都有自己的重量w和价格v，在限定的重量内，如何组合才能使得总价格最高？
or
在总重量不超过w的情况下，总价值能否达到v？

解决实例如下

什么是算法？ 一些列通过计算来解决问题的明确步骤
什么是最好的解决方法？ 更好的性能，那如何衡量性能？
举例for循环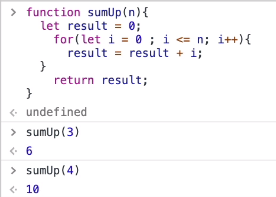

使用Performance提供的api来测量
Performance.now()返回当前时间的时间戳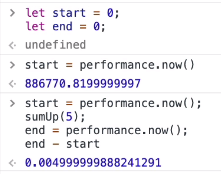

我们不关心具体数字的值，而是它的趋势和方向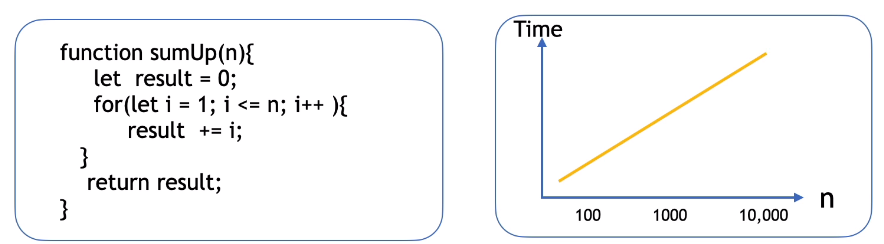

最通用的时间复杂度和空间复杂度分析方法：大O符号

大O符号衡量性能

时间复杂度

常见的是蓝线处的几种复杂度，红线处的则需要被优化

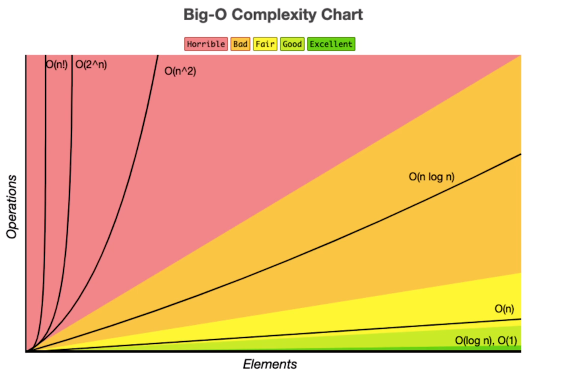
在计算复杂度的时候，O(1)一般会被忽略，因为复杂度是看最高的那个，除非整个算法都是O(1)级别

不是嵌套的for循环也属于O(n)，只是2n，3n的区别
数组的splice方法等会改变原数组的api，也计入时间复杂度O(n)
这种嵌套情况也是O(n)，只是两个循环分摊了一个循环工作，共同完成一个循环

注意：排序具体也分时间空间复杂度操作，若只涉及到编程语言自带的api，则就是N log n 复杂度

O(n^3) 四数之和最优情况
O(2^n) 树中常见，每层有两种分裂情况

1. O(n)遍历的数组是否排好序了？若排好序，则可使用二分搜索，把复杂度降到O(logn)
2. 有道题需要排序去解，能否通过数组、Set、Map去解

3. 遇到嵌套循环，能否先排序？再通过一个for循环

   
   总结：基本就是看for循环的复杂度

空间复杂度

注意：

• 若自定义了长度为固定的的数组，也只是O(1)复杂度，如长度为1/2等
• 题目自己给我们的数据复杂度不计入题内，关注的是做题者在做题过程有无创建复杂度的数据

总结：大部分题都是O(1)复杂度

取舍问题

一般是取时间复杂度的较低的解法，以空间换时间，空间较廉价，除非题目要求“原地算法”

数组

两数之和

输入一个数组，给定一个目标值，在该数组中找出 和为目标值 的两个整数，返回由它们的数组下标构成的数组

思路：

盛水最多的容器

接雨水

字符串

无重复字符的最长子串

子串和子序列的区别
子串：原序列中必须连续的一段
子序列：原序列中可以不连续的一段
无论是子串和子序列，元素的顺序都是原序列的顺序

如：
“abcbbd”子串是abc
“abcbbd”子序列是abcd，即除去连续的子串

滑动窗口技术

滑动窗口技术，本质是双指针作为窗口的两边边界值，在序列数据的某些部分上形成一个窗口，然后在整个数据中移动该窗口以捕获其中的不同部分

链表

链表相比数组的优缺点？
链表的增删改操作比数组快捷方便，只需要node.next改变指向即可，数组需要移位，链表的缺点是查，需要不断的点next以访问到下一个节点

单向链表

尾部指向null

双向链表

尾部n指向n-1，n-1指向n-2

循环链表

举例：尾部n指向头部1，但不一定是尾部指向头部，只要链表某处有构成环状结构即可

二叉树和二叉搜索树

80%的题

二叉树

最后的节点叫叶子，最顶部的一个节点是根
移动当前节点：node = root.right.left.left….

完全二叉树full binary tree

除最底层外，其他各层的子节点数都达到最大个数，且最底层从左到右的叶节点连续存在，只缺右侧若干节点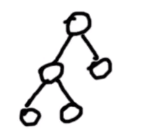

完美/满 二叉树complete binary tree

除了叶节点外，每个节点都有左右子叶，并且叶节点都在最底层的二叉树
（完美二叉树是特殊的完全二叉树）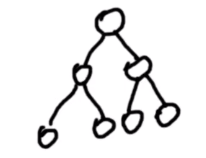

二叉搜索树binary search tree（BST）

非空左子树的所有键值小于其根节点的键值
非空右子树的所有键值大于其根节点的键值
左右子树本身也是二叉搜索树

注意：

• 不可只着眼于一层关系
• 二叉搜索树和递归算法是天然融合的，解二叉搜索树有助于理解递归算法

刷题

步骤

验证约束条件
编写测试例子

• 二分搜索

简单例子：输入排序好的数组和目标值，输出目标值在数组中的index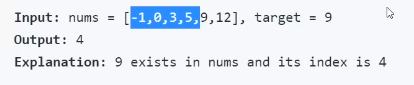

特点：题目一般给定一个排好序的数组，考虑二分搜索，完全乱序数组则不适合

思路：
利用排好序的特征，对半查找，难点在边界值的确定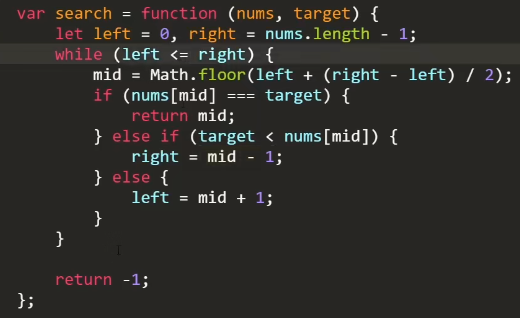

注意：
left + (right + left)/2 //防止值溢出情况，因为整数有最大值
边界值确定的小技巧：试错，根据出错用例进行修改