推理概述
推理:从初始证据出发,按某种策略不断运用知识库中的已知知识,逐步推出结论的过程。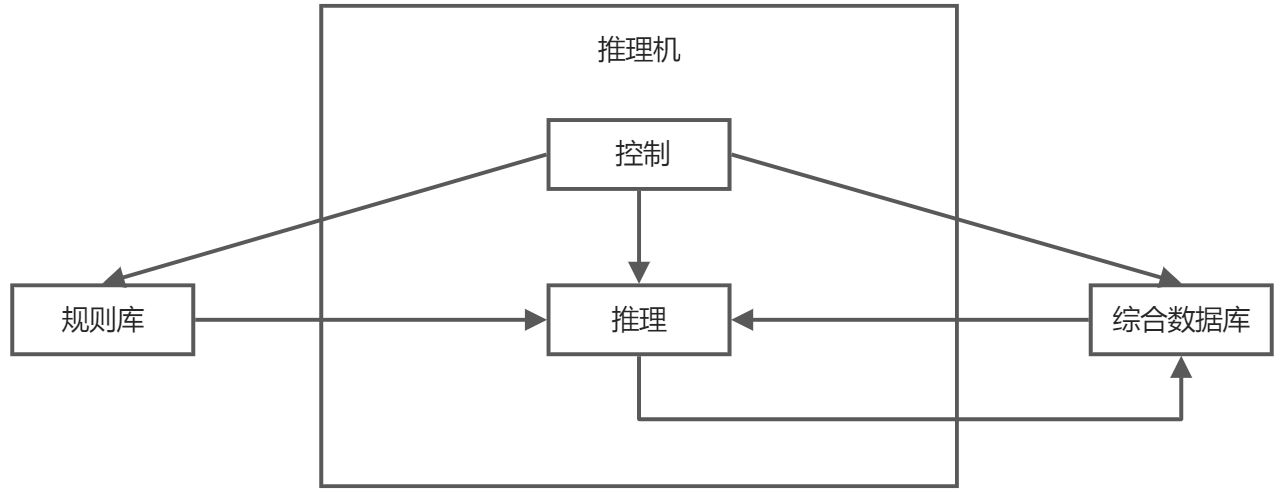
从推出结论的途径
演绎推理
从全称判断推导出单称判断的过程。从一般到个别的推理。
三段论式
大前提:足球运动员身体都是强壮的
小前提:高波是一名足球运动员
结论:高波的身体是强壮的
归纳推理
从足够的多的示例中归纳出一般性结论的推理。从个别到一般的推理。
- 完全归纳推理:全部样本参与
- 不完全归纳推理:抽样
默认推理(缺省推理)
有点儿类似数学归纳法。
在条件A以及成立时,若没有足够的证据证明条件B不成立,则默认B成立,并在此前提下进行推理,若某一时刻发现原先默认不正确,则撤销全部推导出的结论和默认条件。
所用知识的确定性
确定性推理
所用的知识和证据都是确定的,退出的结论也是确定的。
经典逻辑推理
是否越来越接近最终目标
单调推理
非单调推理
在知识不完全的情况下发生的,所以需要做某些假设,并在其基础上进行推理。所以当假设失败时会退回到之前某一步,重新开始。
与推理有关的启发性知识
启发式推理
非启发式推理
冲突消解策略
当(多个)已知事实与知识库中(多个)知识匹配成功,则发生了冲突。按一定的规则从匹配成功的多个知识中挑出一个知识用于当前的推理过程——冲突消解
基本思想:对知识进行排序
按规则的针对性排序
选用针对性较强的产生式规则。若r2中除了r1要求的全部条件外,还包括其他条件,则r2比r1有更大针对性,r1比r2有更大通用性
3个已知事实 r2用了其中三个,产生一个结果 r1用了其中两个,产生一个结果 我们选择r2,因为它用了最全的条件
按已知事实的新鲜性排序
一般把数据库中后添加的事实称为新鲜的事实,新鲜性更大。
设规则r1与事实组A匹配成功,规则r2与事实组B匹配成功,则A与B那一组较新,就采用哪一个规则。
- 逐个比较事实新鲜性,采用多数优先
- 最新鲜事实相比较
- 最不新鲜事实相比较
按匹配对排序
优先采用匹配度较大的产生式规则按条件个数排序
如果有多条产生式规则生成的结论相同,则优先应用条件少的产生式规则,因为其匹配时花费时间较少。
自然演绎推理
从一组已知为真的事实出发,直接运用经典逻辑的推理规则推出结论的过程称为自然推理。
基本的推理是P规则、T规则、假言推理、拒取式推理等。
P规则:就是直接利用推理中给出的前提,即前提引入。
T规则:就是由某一个或几个前提可以通过等价、蕴含得到其他命题公式,即推理规则。
假言推理的形式:
如果X是金属,则X能导电 及 铜是金属,则铜能导电
拒取式:
例1:
设已知如下事实:
- 凡是容易的课程小王都喜欢
- C班的课程都是容易的
- ds是C班的一门课程
求助:小王喜欢ds这门课程
首先定义谓词。
将上述事实及待求职的问题用谓词公式表示
先证ds是容易的课程:
优点:
自然容易理解
缺点:容易产生组合爆炸,推理过程中得到的中间结论呈指数级递增。
谓词公式化为子句集的方法
谓词逻辑中,有如下定义:
原子谓词公式是一个不能再分解的命题,原子谓词公式及其否定,统称为文字(literal),P称为正文字,称为负文字,
与
为互补文字。
子句:任何文字的析取式,任何文字本身也是子句
子句集:由子句构成的集合
空子句:不含任何文字的子句,且是永假的,不可满足的。
在谓词逻辑中,任何一个谓词公式都可以通过应用等价关系及推理规则转换为相应的子句集,从而能够比较容易地判定谓词公式的不可满足性。
定理:谓词公式的不可满足的充要条件是其子句集不可满足——证明子句集不可满足,运用鲁宾孙归结原理
例1:

鲁宾孙归结原理(消解原理)
谓词公式的不可满足性分析转化为子句集中子句的不可满足性分析。而对子句集的不可满足性,需要对子句集中的子句逐一分析,只有当子句对任何非空个体域上的任何一个解释都是不可满足的时候,才能判定该子句是不可满足的,这非常困难。
由于子句集的子句之间是合取关系,当有一个子句不可满足时,整个子句集都不可满足,而空子句是不可满足的,所以当一个子句集包含空子句时,这个子句集一定不可满足。
鲁宾孙归结原理基本方法:检查子句集是否包含空子句,若包含,则不可满足。若不包含,在子句集中选择合适的子句进行归结,一旦通过归结得到空子句,则说明不可满足。
如果没有归结出空子句,则既不能说S不可满足,也不能说S是可满足的。
命题逻辑中的归结原理
设C1与C2是子句集中的任意两个子句,如果C1中的文字L1与C2中的文字L2互补,那么从C1和C2中分别消去L1和L2,并将两个子句中余下的部分析取,构成一个新子句C12,这一过程称为归结。C12称为C1和C2的归结式,C1和C2称为C12的新本子句。
定理1:归结式C12是其亲本子句C1和C2的逻辑结论,即原子句集的不可满足性等价于归结后得到的新子句集的不可满足性。
推论1
推论2
谓词逻辑中的归结原理
由于子句中含有变元,所以不像命题逻辑可以直接消去互补文字,需要先用最一般合一对变元进行代换,然后才能进行归结。
归结反演
归结原理给出了证明子句集不可满足性的方法,根据第二章的知识可知,要证明Q为的逻辑结论,只需证明:



