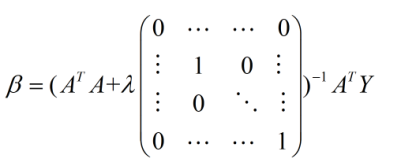广义线性模型Linear Model

引言

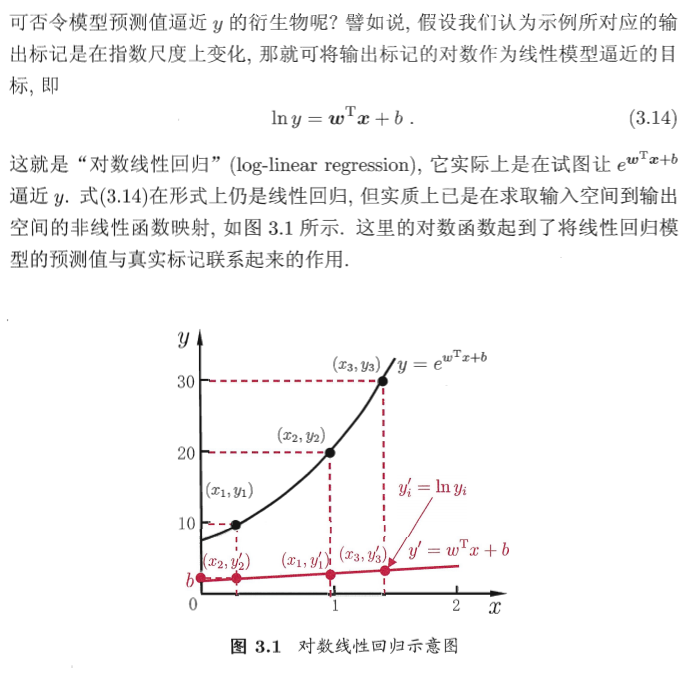
广义线性模型主要用于处理目标值target为特征的线性组合，如果为模型的预测值，则有

为了方便公式推导，将特征系数coef设为，将线性模型在y轴上的截距intercept设为。
线性模型形式简单、易于建模，但却蕴含者机器学习中的一些重要的基本思想，许多功能更为强大的非线性模型（nonlinear model）可在线性模型基础上通过引入层级结构或高维映射而得到，例如多层的神经网络就是在线下分类器的基础上得出。此外，由于系数直观表达了各属性在预测中的重要性，因此线性模型有着很好的可解释性（comprehensibility），因为深层神经网络可解释性较差，所以可解释机器学习现在也是一个研究的热门方向。
线性模型既可以应用于回归任务、也可以应用于分类任务，但目前来看，回归任务还是主流。

机器学习三要素：

• 模型：线性模型
• 策略：损失函数（均方误差、…..）、目标函数（极大似然估计）
• 算法：优化算法，最小二乘法、梯度下降法、牛顿法

  线性回归Linear Regression

  普通最小二乘法

  性能度量Metrics：

  目的是找出一个模型的目标函数或者损失函数
  在回归任务中常用均方误差Mean Square Error：（其他常见的性能度量方式请百度）
  

优化方法（Optimization）：

目的是求解我们定义的目标函数的最优值或者是使得损失函数最小值的参数

最小二乘法（正规方程法）

基于均方误差最小化来求解模型参数的方法被称为最小二乘法（least square）。最小二乘法可以用代数或者几何方式来求解：其实最小二乘法的解法可以理解为我们常说的求导，导数值为0的点有可能为极值点。

• 代数形式，对参数和分别求导，

并使得求导后的结果为0。

这背后的原理为，是关与和的凸函数，当它关于和的导数均为0时，得到和的最优解，也就是使得最小。

• 矩阵形式

再将特征变量也写成向量形式

令 , 对求导得到

令上式为零可以得到最优解的闭式解（closed-form）。
当为满秩矩阵（full-rank matrix）或正定矩阵（positive definite matrix）时，令上式为零可得。

则最终学的的线性回归模型为：

然而，显示任务中往往不是满秩矩阵，有两种可能的情况。

1. 例如在许多任务中我们会遇到大量的变量，其数目甚至超过样例数，导致的列数多与行数，显然不满足秩。
2. 在所有特征中若存在一个特征与另一个特征线性相关或一个特征与若干个特征线性相关时，此时ATA也是不可逆的。

此时可以解出多个，他们都能使均方误差最小化。选择哪一个作为输出，将由学习算法的归纳偏好决定，(1)筛选出线性无关的特征，不保留相同的特征，保证不存在线性相关的特征。 (2)增加样本量。 (3)采用正则化的方法。对于正则化的方法，常见的是L1正则项和L2正则项，L1项有助于从很多特征中筛选出重要的特征，而使得不重要的特征为0(所以L1正则项是个不错的特征选择方法)；如果采用L2正则项的话，实际上解析解就变成了如下的形式：

算法时间复杂度：

使用 X 的奇异值分解来计算最小二乘解。如果 X 是一个形状为 (nsamples, n_features)的矩阵，则

广义线性模型

线性分类

对数几率回归 Logistic Regression

虽然名字是回归，但它解决的确实分类任务。在其他常见中也被称为logit regression, maximum-entropy classification (MaxEnt) 或者 log-linear classifier。
策略（目标函数）：极大似然估计
算法（优化方法）： 梯度下降法或牛顿法或最小二乘法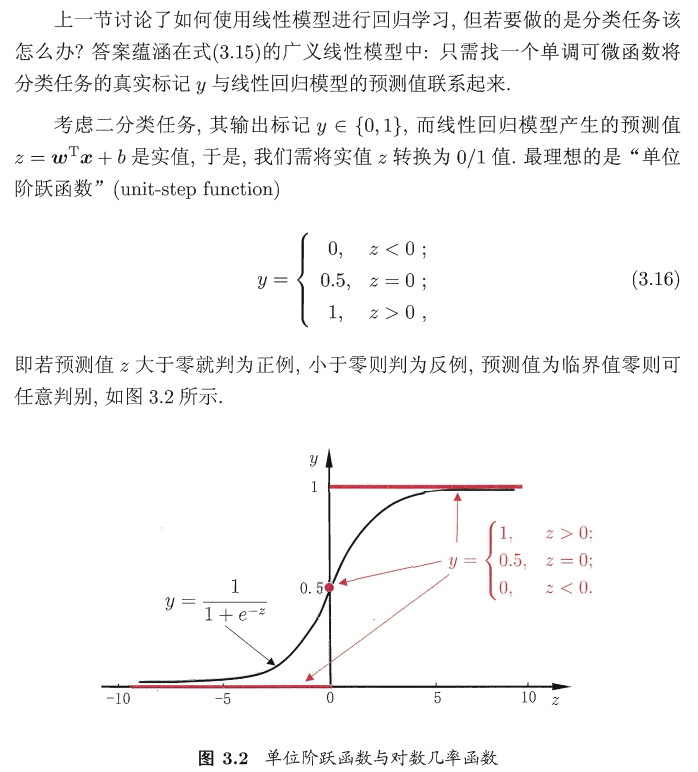

线性判别分析LDA

线性判别分析（Linear Discriminant Analysisi，LDA）是一种经典的线性学习方法，在二分类问题上因为最早由[Fisher,1936]提出，亦称“Fisher判别分析”。
主要思想：给定训练样本，将其降维到二维空间中，设法将样本投影到一条直线，使得同类样本的投影点尽可能接近、异类样本的投影点尽快远离。在对新样本分类时，将其投影到同样的直线上，再根据投影点的位置判断样本的类别。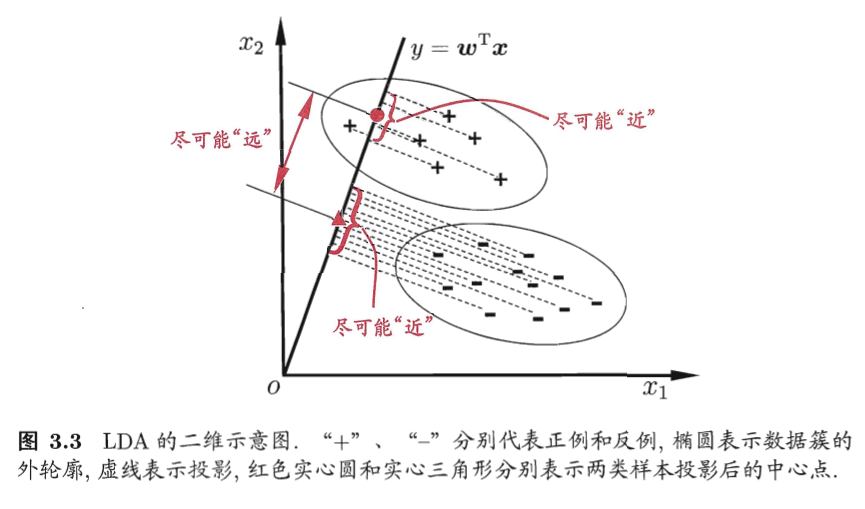

扩展

线性判别分析(discriminant_analysis.LinearDiscriminantAnalysis) 和二次判别分析(discriminant_analysis.QuadraticDiscriminantAnalysis) 是两种经典的分类器，如它们的名字所示，分别具有线性和二次决策平面。
这些分类器之所以有吸引力，是因为它们有一些解析解，可以很容易地计算，本质上是可以扩展至多分类的，在实践中证明工作良好，并且没有需要调优的超参数。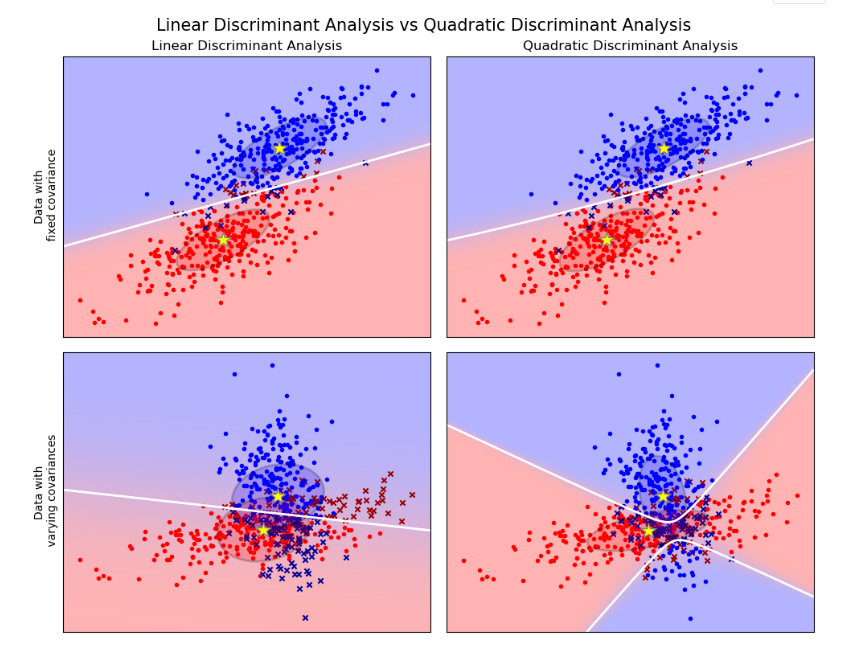

图中给出了线性判别分析和二次判别分析（Quadratic Discriminant Analysis）的决策边界。底部那行证明线性判别分析只能学习线性边界，而二次判别分析可以学习二次边界，因此具有更大的灵活性。

LDA和PCA在鸢尾花数据上降纬

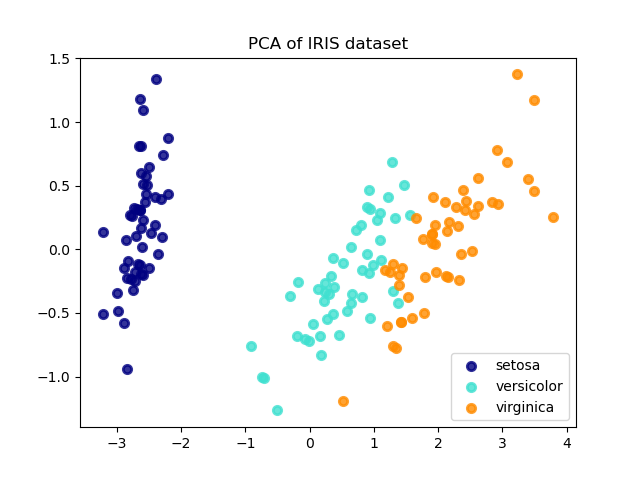
The Iris dataset represents 3 kind of Iris flowers (Setosa, Versicolour and Virginica) with 4 attributes: sepal length, sepal width, petal length and petal width.
Principal Component Analysis (PCA) applied to this data identifies the combination of attributes (principal components, or directions in the feature space) that account for the most variance in the data. Here we plot the different samples on the 2 first principal components.
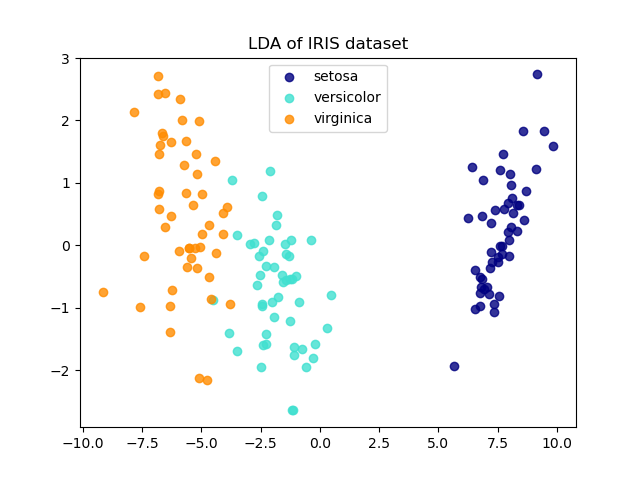
Linear Discriminant Analysis (LDA) tries to identify attributes that account for the most variance between classes. In particular, LDA, in contrast to PCA, is a supervised method, using known class labels.

多分类

有一些二分类学习方法可以直接推广到多分类，但更多情况下，我们是基于一些基本策略，利用二分类学习器来解决多分类问题。分为拆分和测试两个阶段。
一对一（OvO）：将N个类别两两配对，产生N（N-1）/2个二分类任务。
一对其余（OvR）：每次将一个类的样本作为正例，其余类的样本作为反例，训练N个分类器。
多对多（MCM）：纠错输出码（Error Correcting Output Code，ECOC）分为编码和解码阶段。

优化方法分析、

梯度下降法

梯度下降法超参数：初始点、学习率
步骤：

1. 首先设定一个较小的正数步长和一个参数变化量的容忍值tol，以及迭代次数
2. 求当前正数位置处的各个偏导数
3. 迭代修改当前函数的参数值
4. 若参数变化量小于tol或已达迭代次数k，退出，否则返回2

分类：

• 批量梯度下降法BGD：使用全部训练集计算损失函数的梯度，每次全部数据计算梯度更新参数
• 随机梯度下降法SGD ：每次使用一个训练样本更新参数
• 小批量梯度下降法MBGD：每次使用一部分训练样本更新参数 | | BGD | SGD | MBGD | | —- | —- | —- | —- | | 优点 | 非凸函数可保证收敛到全局最优解 | 计算速度快 | 计算速度快，收敛稳定 | | 缺点 | 计算速度缓慢，不允许新样本中途进入 | 计算结果不易收敛，可能会陷入局部最优解 | |

梯度下降法和正规方程法（最小二乘法）

(1)最小二乘法和梯度下降法在线性回归问题中的目标函数是一样的(或者说本质相同)，都是通过最小化均方误差来构建拟合曲线。
(2)二者的不同点可见下图(正规方程就是最小二乘法)：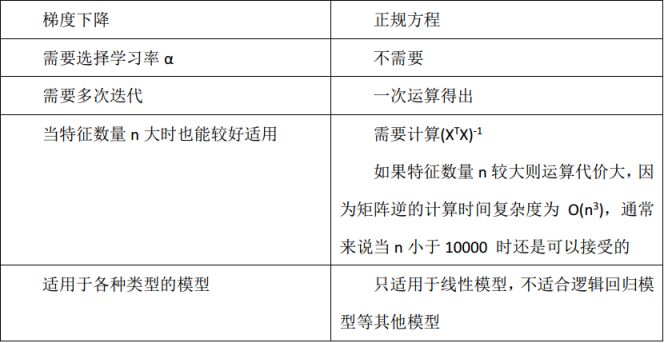

需要注意的一点是最小二乘法只适用于线性模型(这里一般指线性回归)；而梯度下降适用性极强，一般而言，只要是凸函数，都可以通过梯度下降法得到全局最优值(对于非凸函数，能够得到局部最优解)。
梯度下降法只要保证目标函数存在一阶连续偏导，就可以使用。

参考资料

周志华《机器学习》
sklearn-Linear Model
最小二乘法（least sqaure method）
机器学习经典算法&优化算法