二叉树的双旋（左左双旋，右右双旋）

触发条件

如果变化分支的高度比旋转节点的另一侧高度差距超过2，那吗单旋之后依旧不平衡，需要左左双旋或右右双旋

解析

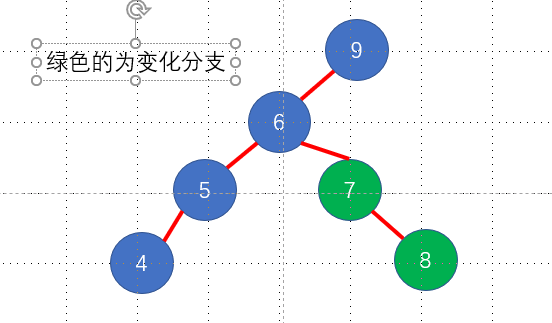
观察上图可得
变化分支的深度为2
旋转节点的另一侧指的就是，根节点9 的右子树，因为变化分支在根节点9的左子树上故另一侧为根节点9的右子树
变化分支的深度 比 旋转节点的深度 差距大于2 符合右右双旋

图例 ：右右双旋

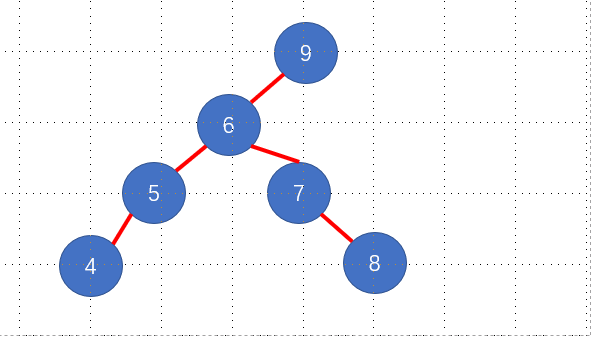
这个二叉树不是平衡二叉树，因为根节点只有左子树，且左子树的深度为三，为此进行右单旋
右单旋后的图示：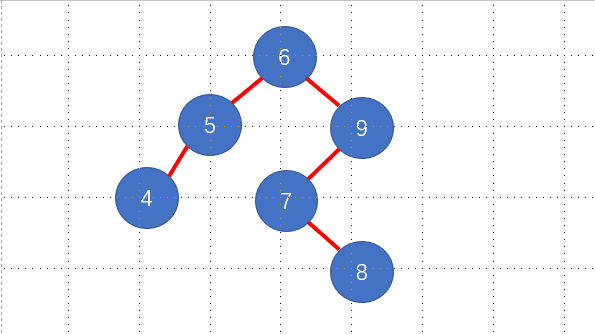

右单旋后你会发现新根节点6 的右子树9不是二叉平衡树因为右子树9的左子树深度为2 右子树深度为0，故无法构成平衡二叉树
将新根节点6的右子树9进行右单旋后到图示：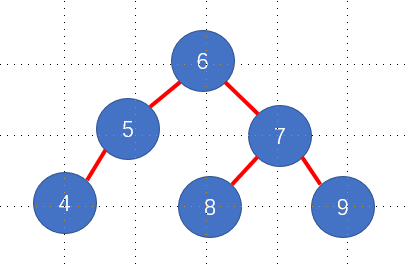


为平衡二叉树
右右单旋的动态示意图

右右双旋

如果变化分支的高度比旋转节点的另一侧高度差距超过2
先进行一次右单旋后，当右单旋后将右子树进行右单旋，之后将整个二叉树判断为是否为平衡二叉树

左左双旋

与右右单旋差不多
如果变化分支的高度比旋转节点的另一侧高度差距超过2
先进行一次左单旋后，当右单旋后将左子树进行左单旋，之后将整个二叉树判断为是否为平衡二叉树

实现代码

class Node {
    constructor(value) {
        this.value = value;
        this.left = null;
        this.right = null;
    }
}
const node9 = new Node('9');
const node8 = new Node('8');
const node7 = new Node('7');
const node6 = new Node('6');
const node5 = new Node('5');
const node4 = new Node('4');
node9.left = node6;
node6.left = node5;
node5.left = node4;
node6.right = node7;
node7.right = node8;
/**
 * 利用单旋将二叉不平衡树变为二叉平衡树
 * @param {*} root 跟节点
 * @returns 返回平衡之后的根节点
 */
function change(root) {
    if (isBalanceTree(root)) return root; // 返回平衡之后的根节点
    // 走到这说明不是二叉平衡树
    // 判断平不平衡需要从下往上判断
    // 判断对二叉树进行平衡操作要按照后序遍历的顺序
    // 后序遍历 先左子树 后右子树 最后自己
    // 为何进行后序遍历，当根节点不是二叉平衡树，可能对子树进行单旋操作就成为二叉平衡树
    if (root.left != null) root.left = change(root.left); // change函数会返回平衡之后的跟节点，故需要接收返回的的根节点
    if (root.right != null) root.right = change(root.right);// change函数会返回平衡之后的跟节点，故需要接收返回的的根节点
    // 获取深度
    let leftTree = getDeep(root.left);
    let rightTree = getDeep(root.right);
    // 判断那里不符合二叉平衡树的要求
    if (Math.abs(leftTree - rightTree) < 2) return root;
    if (leftTree < rightTree) { //左浅 右深 左单旋
        // 获取变化分支的深度
        let changeTree = getDeep(root.right.left)
        // 获取不变分支的深度
        let noChangeTree = getDeep(root.right.right)
        // 当变化分支的深度大于不变化的分支时需要右左双旋
        if (changeTree > noChangeTree) {
            //将右子树进行右单旋
            root.right = rightRotate(root.right)
        }
        // 生成左单旋后的二叉树
        let newRoot =  leftRotate(root)
        // 将其生成后的新二叉树的左子树进行判断
        newRoot.left = change(newRoot.left)
        // 新二叉树的左子树会发生改变，因此将再次判断整个二叉树
        newRoot = change(newRoot)
        return newRoot;
    } else if (leftTree > rightTree) { //左深 右浅 右单旋
        // 获取变化分支的深度
        let changeTree = getDeep(root.left.right)
        // 获取不变分支的深度
        let noChangeTree = getDeep(root.left.left)
        // 当变化分支的深度大于不变化分支的深度将进行左右单旋
        if (changeTree > noChangeTree) {
            // 将其左子树进行左单旋
            root.left = leftRotate(root.left)
        }
        let newRoot =  rightRotate(root);
        // 将其生成后的新二叉树的右子树进行判断
        newRoot.right = change(newRoot.right)
        // 新二叉树的右子树会发生改变，因此将再次判断整个二叉树
        newRoot = change(newRoot)
        return newRoot
    }
    return root
}
/**
 * 判断是否为二叉平衡树
 * 平衡二叉的满足条件
 * 根节点的左子树与右子树的高度差不能超过1
 * 这棵二叉树的每个子树的符合第一条
 * @param {*} root 根节点
 * @returns Boolean
 */
function isBalanceTree(root) {
    if (!root) return true;
    // 获取左右子树的深度
    let left = getDeep(root.left);
    let right = getDeep(root.right);
    // 当左子树与右子树的深度差大于1说明不是二叉平衡树
    if (Math.abs(left - right) > 1) return false;
    // 遍历这个二叉树的每一个子树
    else return isBalanceTree(root.left) && isBalanceTree(root.right);
}
/**
 * 获取二叉树的深度
 * @param {*} root 节点
 * @returns Number 返回左右子树中最深的层数
 */
function getDeep(root) {
    if (!root) return 0;
    let left = getDeep(root.left);
    let right = getDeep(root.right);
    return Math.max(left, right) + 1;
}
/**
 * 左单旋
 * 旋转节点：不平衡的节点为旋转节点
 * 新根：旋转节点的右子树的根节点
 * @param {*} root 旋转节点
 * @returns 新的根节点
 */
function leftRotate(root) {
    // 找到新根
    let newNode = root.right;
    // 找到变化分支
    let changeNode = newNode.left;
    // 当前旋转节点的右孩子为变化分支
    root.right = changeNode;
    // 新根的左孩子为旋转节点
    newNode.left = root;
    // 返回新的根节点
    return newNode;
}
/**
 * 右单旋
 * 旋转节点：不平衡的节点为旋转节点
 * 新根：旋转节点的左子树的根节点
 * @param {*} root 旋转节点
 * @returns 新的根节点
 */
function rightRotate(root) {
    // 找到新根
    let newNode = root.left;
    // 找到变化分支
    let changeNode = newNode.right;
    // 当前旋转节点的左孩子为变化分支
    root.left = changeNode
    // 新根的右孩子为旋转节点
    newNode.right = root;
    // 返回新的根节点
    return newNode;
}
/**
 * 判断是否为平衡二叉树
 * 平衡二叉的满足条件
 * 根节点的左子树与右子树的高度差不能超过1
 * 这棵二叉树的每个子树的符合第一条
 * @param {*} root 节点
 * @returns Boolean
 */
function isBalanceTree(root) {
    if (!root) return true;
    let letTree = getDeep(root.left)
    let rightTree = getDeep(root.right)
    if (Math.abs(letTree - rightTree) > 1) return false
    else return isBalanceTree(root.left) && isBalanceTree(root.right);
}
// 测试右右双旋
let root = change(node9);
console.log(isBalanceTree(root))