首先给出信息熵的定义:
%3D%5Cmathbb%7BE%7D%5BI(X)%5D%5C%5C%3D%5Csum%7Bx%5Cin%20%5Cchi%7Dp(x)%5Clog%5Cfrac%7B1%7D%7Bp(x)%7D%5C%5C%3D-%5Csum%7Bx%5Cin%5Cchi%7Dp(x)%5Clog%20p(x)%20%5Ctag%7B1%7D%0A#card=math&code=H%28X%29%3D%5Cmathbb%7BE%7D%5BI%28X%29%5D%5C%5C%3D%5Csum%7Bx%5Cin%20%5Cchi%7Dp%28x%29%5Clog%5Cfrac%7B1%7D%7Bp%28x%29%7D%5C%5C%3D-%5Csum%7Bx%5Cin%5Cchi%7Dp%28x%29%5Clog%20p%28x%29%20%5Ctag%7B1%7D%0A&id=XGP8U)
其中,为有限个事件
的集合,
是定义在
上的随机变量。
信息熵是随机事件不确定性的度量:事件的概率分布和每个事件的信息量#card=math&code=I%28x%29&id=qheks),也被称作自信息,构成了一个随机变量,这个随机变量的均值(即期望
)就是这个分布产生的信息量的平均值(即熵)。
这里,%3D%5Clog_2(%5Cfrac%7B1%7D%7Bp(x)%7D)#card=math&code=I%28x%29%3D%5Clog_2%28%5Cfrac%7B1%7D%7Bp%28x%29%7D%29&id=xiAcl)是样本携带的信息量的大小。一个较小概率事件发生的时候的信息量较大,一个必然事件发生的时候的信息量较小。而作为整个事件集合的不确定性的度量,非必然且非不可能的事件发生的越多也就意味着更多的不确定性,因此会有更高的信息熵熵值。
由此可以引出针对两个变量和
之间的联合熵:
%3D-%5Csum%7Bx%5Cin%5Cchi%7D%5Csum%7By%5Cin%20Y%7Dp(x%2Cy)%5Clog%20p(x%2Cy)%3D%5Cmathbb%7BE%7D%5BI(p(x%2Cy)%5D%20%5Ctag%7B2%7D%0A#card=math&code=H%28X%2CY%29%3D-%5Csum%7Bx%5Cin%5Cchi%7D%5Csum%7By%5Cin%20Y%7Dp%28x%2Cy%29%5Clog%20p%28x%2Cy%29%3D%5Cmathbb%7BE%7D%5BI%28p%28x%2Cy%29%5D%20%5Ctag%7B2%7D%0A&id=e1epj)
可以推出:
%3DH(X)%2BH(Y%7CX)%20%5Ctag%7B3%7D%0A#card=math&code=H%28X%2CY%29%3DH%28X%29%2BH%28Y%7CX%29%20%5Ctag%7B3%7D%0A&id=KHCJY)
联合熵的物理意义就是,观察一个多个随机变量的随机系统获得的信息量。
可以引出两个变量和
之间的条件熵:
%3D-%5Csum%7Bx%5Cin%5Cchi%7D%5Csum%7By%5Cin%20Y%7Dp(x%2Cy)%5Clog%20%5Cfrac%7Bp(x%2Cy)%7D%7Bp(y)%7D%5C%5C%3D-%5Csum%7Bx%5Cin%5Cchi%7D%5Csum%7By%5Cin%20Y%7Dp(x%2Cy)%5Clog%20p(x%7Cy)%20%5Ctag%7B4%7D%0A#card=math&code=H%28Y%7CX%29%3D-%5Csum%7Bx%5Cin%5Cchi%7D%5Csum%7By%5Cin%20Y%7Dp%28x%2Cy%29%5Clog%20%5Cfrac%7Bp%28x%2Cy%29%7D%7Bp%28y%29%7D%5C%5C%3D-%5Csum%7Bx%5Cin%5Cchi%7D%5Csum%7By%5Cin%20Y%7Dp%28x%2Cy%29%5Clog%20p%28x%7Cy%29%20%5Ctag%7B4%7D%0A&id=wpYGl)
条件熵的贝叶斯规则描述为:
%3DH(X%7CY)-H(X)%2BH(Y)%20%5Ctag%7B5%7D%0A#card=math&code=H%28Y%7CX%29%3DH%28X%7CY%29-H%28X%29%2BH%28Y%29%20%5Ctag%7B5%7D%0A&id=D0ztA)
条件熵的链式法则为:
%3DH(X%2CY)-H(X)%20%5Ctag%7B6%7D%0A#card=math&code=H%28Y%7CX%29%3DH%28X%2CY%29-H%28X%29%20%5Ctag%7B6%7D%0A&id=a0TS1)
条件熵的物理意义为,在得知某一确定信息的基础上获取另外一个信息时所获得的信息量。
因此当且仅当 的值完全由
确定时,
%3D0%7D#card=math&code=%7B%5Cdisplaystyle%20%5Cmathrm%20%7BH%7D%20%28Y%7CX%29%3D0%7D&id=K8z2N)。相反,当且仅当
和
为独立随机变量时
%3D%5Cmathrm%20%7BH%7D%20(Y)%7D#card=math&code=%7B%5Cdisplaystyle%20%5Cmathrm%20%7BH%7D%20%28Y%7CX%29%3D%5Cmathrm%20%7BH%7D%20%28Y%29%7D&id=op0LM)。
给定任何两个随即变量,
,如果联合分布为
#card=math&code=p%28x%2Cy%29&id=BZ0Lq),边缘分布为
#card=math&code=p%28x%29&id=ncMsJ),
#card=math&code=p%28y%29&id=gusP4),则互信息可以定义为:
%3D%5Csum%7Bx%5Cin%20%5Cchi%7D%5Csum%7By%5Cin%20Y%7Dp(x%2Cy)%5Clog%5Cfrac%7Bp(x%2Cy)%7D%7Bp(x)p(y)%7D%20%5Ctag%7B7%7D%0A#card=math&code=I%28X%3BY%29%3D%5Csum%7Bx%5Cin%20%5Cchi%7D%5Csum%7By%5Cin%20Y%7Dp%28x%2Cy%29%5Clog%5Cfrac%7Bp%28x%2Cy%29%7D%7Bp%28x%29p%28y%29%7D%20%5Ctag%7B7%7D%0A&id=JifYA)
对于互信息的定义的推导如下:
%3D%5Csum%7Bx%5Cin%20%5Cchi%7D%5Csum%7By%5Cin%20Y%7Dp(x%2Cy)%5Clog%5Cfrac%7Bp(x%2Cy)%7D%7Bp(x)p(y)%7D%20%5Ctag%7B8%7D%20%5C%5C%20%3D%5Csum%7Bx%5Cin%20%5Cchi%7D%5Csum%7By%5Cin%20Y%7Dp(x%2Cy)%5Clog%20%5Cfrac%7Bp(x%2Cy)%7D%7Bp(x)%7D-%5Csum%7Bx%5Cin%20%5Cchi%7D%5Csum%7By%5Cin%20Y%7Dp(x%2Cy)%5Clog%20p(y)%5C%5C%3D%5Csum%7Bx%5Cin%20%5Cchi%7D%5Csum%7By%5Cin%20Y%7Dp(x)p(y%7Cx)%5Clog%20p(y%7Cx)-%5Csum%7Bx%5Cin%20%5Cchi%7D%5Csum%7By%5Cin%20Y%7Dp(x%2Cy)%5Clog%20p(y)%5C%5C%3D%5Csum%7Bx%5Cin%5Cchi%7Dp(x)(%5Csum%7Bx%5Cin%5Cchi%7D%5Csum%7By%5Cin%20Y%7Dp(y%7Cx)%5Clog%20p(y%7Cx))-%5Csum%7By%5Cin%20Y%7D%5Clog%20p(y)(%5Csum%7Bx%5Cin%20%5Cchi%7Dp(x%2Cy))%5C%5C%3D-%5Csum%7Bx%5Cin%5Cchi%7Dp(x)H(Y%7CX%3Dx)-%5Csum%7By%5Cin%20Y%7D%5Clog%20p(y)p(y)%5C%5C%3D-H(Y%7CX)%2BH(Y)%5C%5C%3DH(Y)-H(Y%7CX)%5C%5C%3DH(X)-H(X%7CY)%0A#card=math&code=I%28X%3BY%29%3D%5Csum%7Bx%5Cin%20%5Cchi%7D%5Csum%7By%5Cin%20Y%7Dp%28x%2Cy%29%5Clog%5Cfrac%7Bp%28x%2Cy%29%7D%7Bp%28x%29p%28y%29%7D%20%5Ctag%7B8%7D%20%5C%5C%20%3D%5Csum%7Bx%5Cin%20%5Cchi%7D%5Csum%7By%5Cin%20Y%7Dp%28x%2Cy%29%5Clog%20%5Cfrac%7Bp%28x%2Cy%29%7D%7Bp%28x%29%7D-%5Csum%7Bx%5Cin%20%5Cchi%7D%5Csum%7By%5Cin%20Y%7Dp%28x%2Cy%29%5Clog%20p%28y%29%5C%5C%3D%5Csum%7Bx%5Cin%20%5Cchi%7D%5Csum%7By%5Cin%20Y%7Dp%28x%29p%28y%7Cx%29%5Clog%20p%28y%7Cx%29-%5Csum%7Bx%5Cin%20%5Cchi%7D%5Csum%7By%5Cin%20Y%7Dp%28x%2Cy%29%5Clog%20p%28y%29%5C%5C%3D%5Csum%7Bx%5Cin%5Cchi%7Dp%28x%29%28%5Csum%7Bx%5Cin%5Cchi%7D%5Csum%7By%5Cin%20Y%7Dp%28y%7Cx%29%5Clog%20p%28y%7Cx%29%29-%5Csum%7By%5Cin%20Y%7D%5Clog%20p%28y%29%28%5Csum%7Bx%5Cin%20%5Cchi%7Dp%28x%2Cy%29%29%5C%5C%3D-%5Csum%7Bx%5Cin%5Cchi%7Dp%28x%29H%28Y%7CX%3Dx%29-%5Csum%7By%5Cin%20Y%7D%5Clog%20p%28y%29p%28y%29%5C%5C%3D-H%28Y%7CX%29%2BH%28Y%29%5C%5C%3DH%28Y%29-H%28Y%7CX%29%5C%5C%3DH%28X%29-H%28X%7CY%29%0A&id=M0xWz)
其中,#card=math&code=H%28X%29&id=EHA0L)是随机变量
的信息量,
#card=math&code=H%28X%7CY%29&id=qUCul)是知道事实
之后
所拥有的信息量,因此互信息
#card=math&code=I%28X%3BY%29&id=RZT16)就是知道事实
之后
的信息量减少的量:
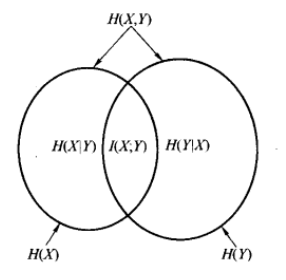
因此如果随机变量和
相互独立,则它们之间的互信息
%3DI(Y%3BX)%3D0#card=math&code=I%28X%3BY%29%3DI%28Y%3BX%29%3D0&id=kskfX)。
互信息可以看成是一个随机变量中包含的关于另一个随机变量的信息量,或者说是一个随机变量由于已知另一个随机变量而减少的不肯定性 。
在上文的基础上,给出更加常用的在两个概率分布之间的相对熵与交叉熵。
在两个概率密度函数#card=math&code=p%28x%29&id=l4Imt)和
#card=math&code=q%28x%29&id=we9jx)之间的相对熵定义为:
%3D%5Csum%7Bx%5Cin%5Cchi%7Dp(x)%5Clog%20%5Cfrac%7Bp(x)%7D%7Bq(x)%7D%20%5Ctag%7B9%7D%5C%5C%3DH(p%2Cq)-H(p)%0A#card=math&code=D%7BKL%7D%28p%7C%7Cq%29%3D%5Csum_%7Bx%5Cin%5Cchi%7Dp%28x%29%5Clog%20%5Cfrac%7Bp%28x%29%7D%7Bq%28x%29%7D%20%5Ctag%7B9%7D%5C%5C%3DH%28p%2Cq%29-H%28p%29%0A&id=j2IV1)
相对熵可以衡量不同策略之间的差异,因为其衡量两个取值为正的函数或概率分布之间的差异,可以计算某个策略和最优策略之间的差异。
基于相同事件测度的两个概率分布和
的交叉熵是指,当基于一个“非自然”(相对于“真实”分布
而言)的概率分布
进行编码时,在事件集合中唯一标识一个事件所需要的平均比特数:
%3D-%5Csum%7Bx%5Cin%5Cchi%7Dp(x)%5Clog%20q(x)%5C%5C%3DH(p)%2BD%7BKL%7D(p%7C%7Cq)%20%5Ctag%7B10%7D%0A#card=math&code=H%28p%2Cq%29%3D-%5Csum%7Bx%5Cin%5Cchi%7Dp%28x%29%5Clog%20q%28x%29%5C%5C%3DH%28p%29%2BD%7BKL%7D%28p%7C%7Cq%29%20%5Ctag%7B10%7D%0A&id=hCyJI)
交叉熵越低,这个策略就越好,最低的交叉熵也就是使用了真实分布所计算出来的信息熵,因为此时%3D(x)#card=math&code=p%28x%29%3D%28x%29&id=ccZmC),交叉熵 = 信息熵。这也是为什么在机器学习中的分类算法中,我们总是最小化交叉熵,因为在同一个随即变量上的估计的概率分布与真实的概率分布之间的 交叉熵越低,就证明由算法所产生的策略最接近最优策略,也间接证明我们算法所算出的非真实分布越接近真实分布。

