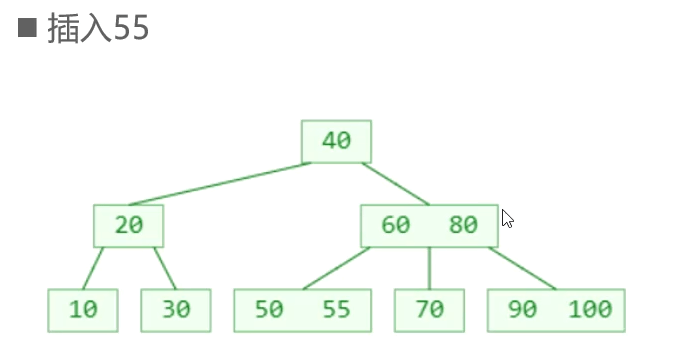
1.复杂度

算法是用于解决特定问题的一系列的执行步骤
使用不同的算法，解决同一个问题，效率可能会相差非常大

例如:求斐波那契额数 (注意：n是从0开始的)
/**
* 0 1 1 2 3 5 8 13 …
* 求斐波那契额数 函数表达式 f(n)=f(n-1)+f(n-2) n>2时 ; n<2时 f(1)=0 f(2)=1
* 使用递归算法,可以先求出函数表达式,直接套进去
*/

  1. public static Integer fib1(Integer n) {
  2.         if (n <= 1) {
  3.             return n;
  4.         }
  5.         return fib1(n - 1) + fib1(n - 2);
  6. }

/**
* 0 1 1 2 3 5 8 13 …
* 使用for循环 n从0开始
*/

  1.  public static Integer fib2(Integer n) {
  2.         if (n == 1) {
  3.             return 0;
  4.         }
  5.         Integer first = 0;
  6.         Integer second = 1;
  7.         //第n个数等于需要加n-1次
  8.         for (int i = 0; i < n - 1; i++) {
  9.             int sum = first + second;
  10.             first = second;
  11.             second = sum;
  12.         }
  13.         return second;
  14.     }

综上对比，当n的数量大的时候，for循环方式要快很多

如何评判一个算法的好坏？
如果单从执行效率上进行评估，可能会想到这么一种解决方案
比较不同算法对同一组输入的执行处理时间
这种方案也叫作:事后统计法

一般从以下维度来评估算法的优劣
正确性、可读性、健壮性(对不合理输入的反应能力)
时间复杂度(time complexity):估算程序指令的执行次数(执行时间)
空间复杂度(space complexity):估算所需占用的存储空间

大O表示法(Big O)
一般用大O表示法来描述复杂度，它表示的是数据规模n对应的复杂度

时间复杂度:
忽略常数、系数、低阶、
9 >>> O(1)
2n+3 >>> O(n)
n²+2n+6 >>>O(n²)
4n³+3n²+22n+100 >>>O(n³)
log5(n) >>>log(n)
常见复杂度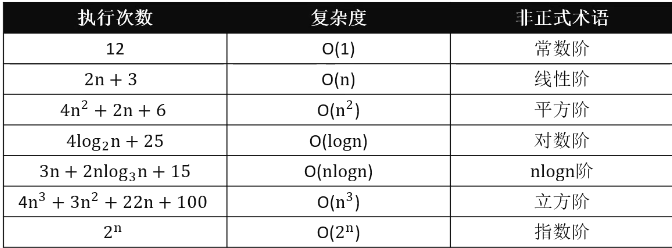
image.png
O(1)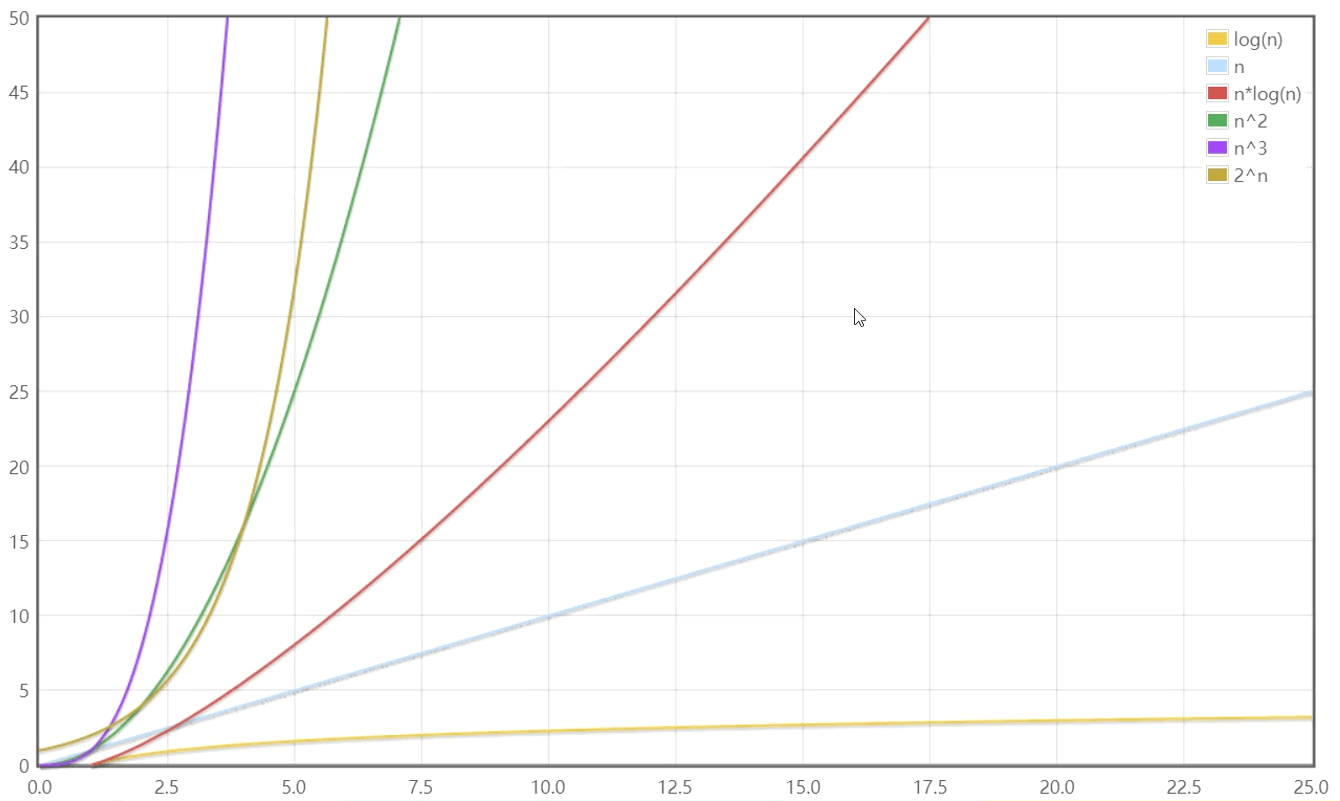 数据模型
image.png空间复杂福
计算斐波那契数递归算法的时间复杂度:
例如:计算n=5的值
1+2+4+8=2^0+2^1+2^2+2^3=2^4-1=2^(n-1)-1
所以时间复杂度是O(2^n)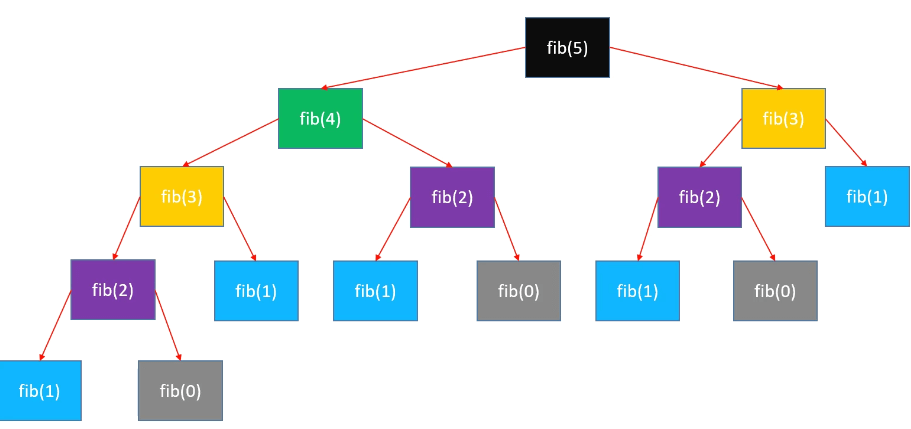
image.png
每次执行一次函数都是做一次加法，只需要计算调用多少次就行
image.png有的时候算法之间的差距，往往比硬件方面的差距还要大

算法优化的方向:
用尽量少的存储空间
用尽量少的执行步骤(执行时间)
根据情况可以空间换时间，时间换空间

多规模数据的情况
image.png
leetcode:一个用于练习算法的好网站
https://leetcode.com
https://leetcode-cn.com

2.动态数组

什么是数据结构?
数据结构是计算机存储，组织数据的方式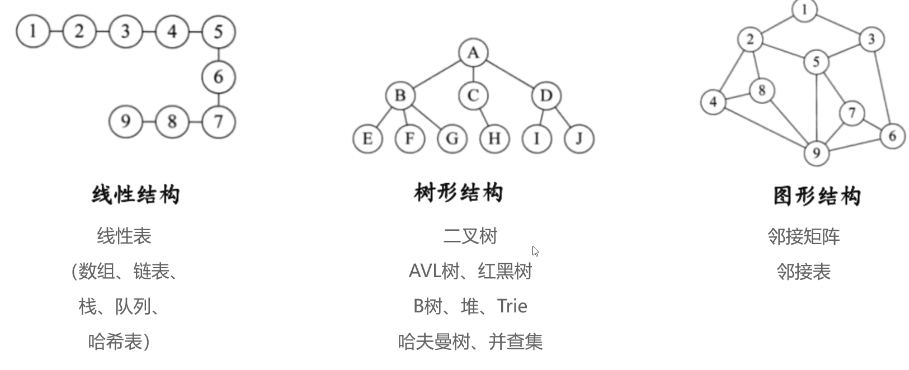
image.png
线性表是具有n个相同类型元素的有限序列(n>=0)image.png

数组（Array）
数组是一种顺序存储的线性表，所有的元素内存地址都是连续的
int[] array =new int[]{11,22,33};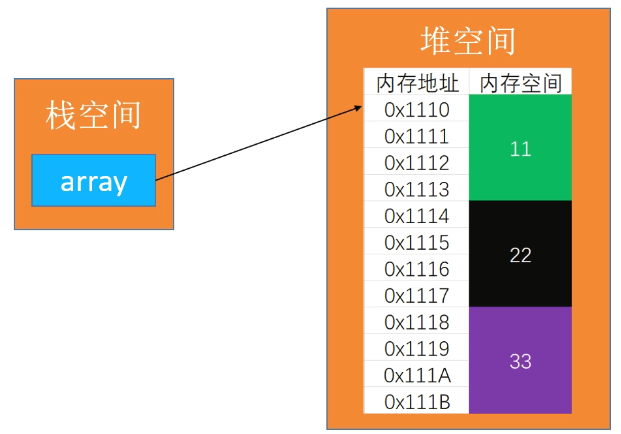
image.png
在很多变成语言中，数组都有个致命的缺点，无法动态修改容量，需要使用动态数组。

动态数组(Dynamic Array)接口设计:
需要的常量:size(数组长度)、elements(声明的数组)、数组默认长度等

add方法原理:
image.png

  1.    /**
  2.      * 添加元素到尾部
  3.      * @param element
  4.      */
  5.     public void add(int element) {
  6.         elements[size++] = element;
  7.     }

remove方法原理：

image.png

  1.     /**
  2.      * 移除该索引的元素
  3.      * @param index
  4.      * @return
  5.      */
  6.     public int remove(int index) {
  7.         if (index < 0 || index >= size) {
  8.             throw new IndexOutOfBoundsException("Index:" + index + ",Size:" + size);
  9.         }
  10.         for (int i = index; i < size - 1; i++) {
  11.             elements[i] = elements[i + 1];
  12.         }
  13.         size--;
  14.         return 1;
  15.     }

add根据索引插入数据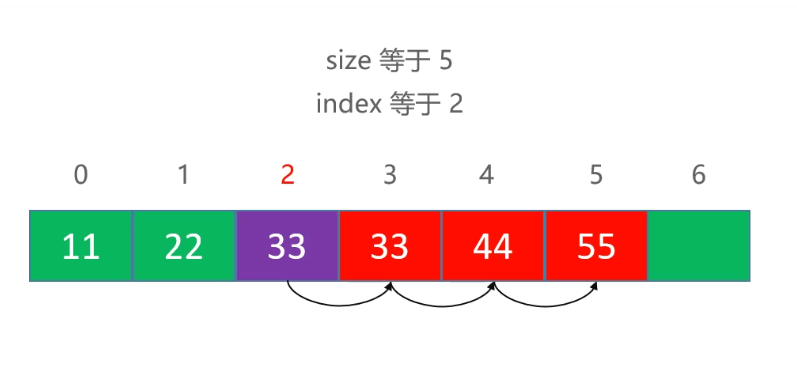
image.png

  1. /**
  2.      * 根据索引添加元素
  3.      *
  4.      * @param element
  5.      */
  6.     public void add(int index, int element) {
  7.         if (index < 0 || index >size) {
  8.             throw new IndexOutOfBoundsException();
  9.         }
  10.         for (int i = size; i > index; i--) {
  11.             elements[i] = elements[i - 1];
  12.         }
  13.         elements[index] = element;
  14.         size++;
  15.     }

动态扩容
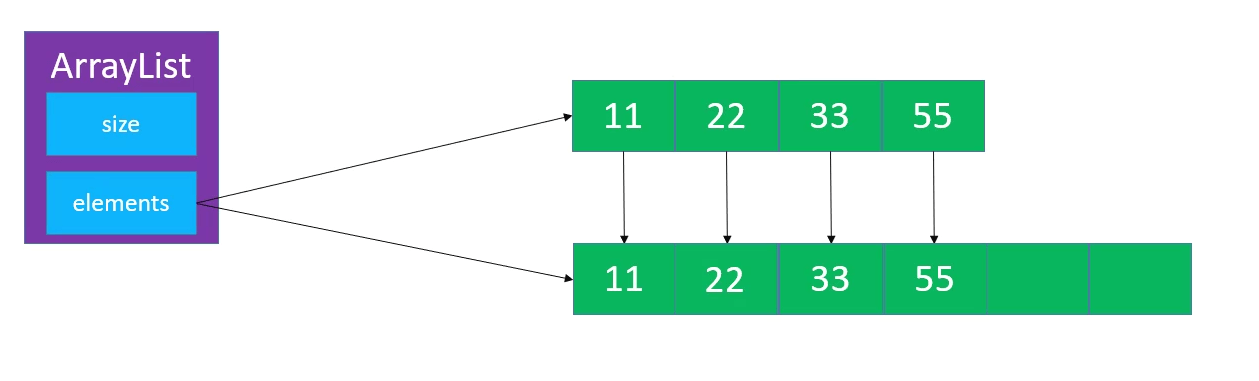
image.png

当数组的长度不足的时候，需要扩容，否则会报错，Arraylist扩容的长度为原长度的1.5倍
两个方法需要使用扩容:
在list后面添加数据:add(String element)
根据索引插入数据:add(int index,String element) 

  1.    /**
  2.      * 添加元素到尾部
  3.      *
  4.      * @param element
  5.      */
  6.     public void add(int element) {
  7.         add(size,element);
  8.     }
  9.     /**
  10.      * 根据索引添加元素 
  11.      * @param element
  12.      */
  13.     public void add(int index, int element) {
  14.         rangCheckForAdd(index);
  15.         ensureCapacity(size+1);
  16.         for (int i = size; i > index; i--) {
  17.             elements[i] = elements[i - 1];
  18.         }
  19.         elements[index] = element;
  20.         size++;
  21.     }
  22.    /**
  23.      * 检查添加时候的索引判断,因为添加的时候索引可以等于list的长度
  24.      * @param index
  25.      */
  26.     private void rangCheckForAdd(int index){
  27.         if (index < 0 || index > size) {
  28.             throw new IndexOutOfBoundsException("Index:" + index + ",Size:" + size);
  29.         }
  30.     }
  31.    /**
  32.      * 数组扩容
  33.      * @param capacity
  34.      */
  35.     private void ensureCapacity(int capacity) {
  36.         int oldCapacity = elements.length;
  37.         if(oldCapacity>=capacity){ return;}
  38.         int newCapacity=oldCapacity+(oldCapacity>>1);
  39.         int[] newElements=new int[newCapacity];
  40.         for (int i = 0; i < oldCapacity; i++) {
  41.             newElements[i] = elements[i];
  42.         }
  43.         elements=newElements;
  44.     }

动态数组加泛型
使用泛型技术可以让动态数组更加通用，可以存放任何数据类型

  1. package com.ruoyi.Algorithms.f2动态数组;
  3. /**
  4.  * 自己手动写一个动态数组
  5.  */
  6. public class ArrayList<E> {
  7.     /**
  8.      * 元素的数量
  9.      */
  10.     private int size;
  11.     /**
  12.      * 所有的元素
  13.      */
  14.     private E[] elements;
  16.     private static final int DEFAULT_CAPACITY = 10;
  18.     private static final int ELEMENT_NOT_FOUND = -1;
  20.     /**
  21.      * 构造方法初始化数组,如果小于10则为大小为10
  22.      *
  23.      * @param capacity
  24.      */
  25.     public ArrayList(int capacity) {
  26.         capacity = Math.max(capacity, DEFAULT_CAPACITY);
  27.         elements = (E[]) new Object[capacity];
  28.     }
  30.     /**
  31.      * 构造方法初始化数组
  32.      */
  33.     public ArrayList() {
  34.         this(DEFAULT_CAPACITY);
  35.     }
  37.     /**
  38.      * 添加元素到尾部
  39.      *
  40.      * @param element
  41.      */
  42.     public void add(E element) {
  43.         add(size,element);
  44.     }
  47.     /**
  48.      * 根据索引添加元素
  49.      * @param element
  50.      */
  51.     public void add(int index, E element) {
  52.         rangCheckForAdd(index);
  53.         ensureCapacity(size+1);
  54.         for (int i = size; i > index; i--) {
  55.             elements[i] = elements[i - 1];
  56.         }
  57.         elements[index] =element;
  58.         size++;
  59.     }
  61.     /**
  62.      * 数组扩容
  63.      * @param capacity
  64.      */
  65.     private void ensureCapacity(int capacity) {
  66.         int oldCapacity = elements.length;
  67.         if(oldCapacity>=capacity){ return;}
  68.         int newCapacity=oldCapacity+(oldCapacity>>1);
  69.         E[] newElements= (E[]) new Object[newCapacity];
  70.         for (int i = 0; i < oldCapacity; i++) {
  71.             newElements[i] = elements[i];
  72.         }
  73.         elements=newElements;
  74.     }
  76.     /**
  77.      * 设置index位置的元素
  78.      *
  79.      * @param index
  80.      * @param element
  81.      * @return
  82.      */
  83.     public E set(int index, E element) {
  84.         rangCheck(index);
  85.         E oldelement = elements[index];
  86.         elements[index] = element;
  87.         return oldelement;
  88.     }
  90.     /**
  91.      * 获取index位置的元素
  92.      *
  93.      * @param index
  94.      * @return
  95.      */
  96.     public E get(int index) {
  97.         if (index < 0 || index >= size) {
  98.             throw new IndexOutOfBoundsException("Index:" + index + ",Size:" + size);
  99.         }
  100.         return elements[index];
  101.     }
  103.     /**
  104.      * 移除该索引的元素
  105.      *
  106.      * @param index
  107.      * @return
  108.      */
  109.     public int remove(int index) {
  110.         rangCheck(index);
  111.         for (int i = index; i < size - 1; i++) {
  112.             elements[i] = elements[i + 1];
  113.         }
  114.         size--;
  115.         return 1;
  116.     }
  118.     /**
  119.      * 查看元素的索引
  120.      *
  121.      * @param element
  122.      * @return
  123.      */
  124.     public int indexOf(E element) {
  125.         for (int i = 0; i < elements.length; i++) {
  126.             if (elements[i] == element) return i;
  127.         }
  128.         return ELEMENT_NOT_FOUND;
  129.     }
  131.     /**
  132.      * 是否包含这个元素
  133.      *
  134.      * @param element
  135.      * @return
  136.      */
  137.     public boolean contains(E element) {
  138.         return indexOf(element) != ELEMENT_NOT_FOUND;
  139.     }
  141.     /**
  142.      * 是否为空
  143.      *
  144.      * @return
  145.      */
  146.     public boolean isEmpty() {
  147.         return size == 0;
  148.     }
  150.     /**
  151.      * 清除所有元素
  152.      *
  153.      * @return
  154.      */
  155.     public void clear() {
  156.         size = 0;
  157.     }
  159.     public int size() {
  160.         return size;
  161.     }
  163.     /**
  164.      * 打印数组的元素
  165.      */
  166.     @Override
  167.     public String toString() {
  168.         StringBuilder sb = new StringBuilder();
  169.         sb.append("size=").append(size).append(",[");
  170.         for (int i = 0; i < size; i++) {
  171.             sb.append(elements[i]);
  172.             if (i != size - 1) {
  173.                 sb.append(",");
  174.             }
  175.         }
  176.         sb.append("]");
  177.         return sb.toString();
  178.     }
  180.     /**
  181.      * 检查范围
  182.      * @param index
  183.      */
  184.     private void rangCheck(int index){
  185.         if (index < 0 || index >= size) {
  186.             throw new IndexOutOfBoundsException("Index:" + index + ",Size:" + size);
  187.         }
  188.     }
  190.     /**
  191.      * 检查添加时候的索引判断,因为添加的时候索引可以等于list的长度
  192.      * @param index
  193.      */
  194.     private void rangCheckForAdd(int index){
  195.         if (index < 0 || index > size) {
  196.             throw new IndexOutOfBoundsException("Index:" + index + ",Size:" + size);
  197.         }
  198.     }
  199. }

对象数组

数组里面的空间都是连续的，不是存储的对象，而是存储的内存地址，
可以节省空间，当需要删除对象的时候，直接清空数组的引用就行了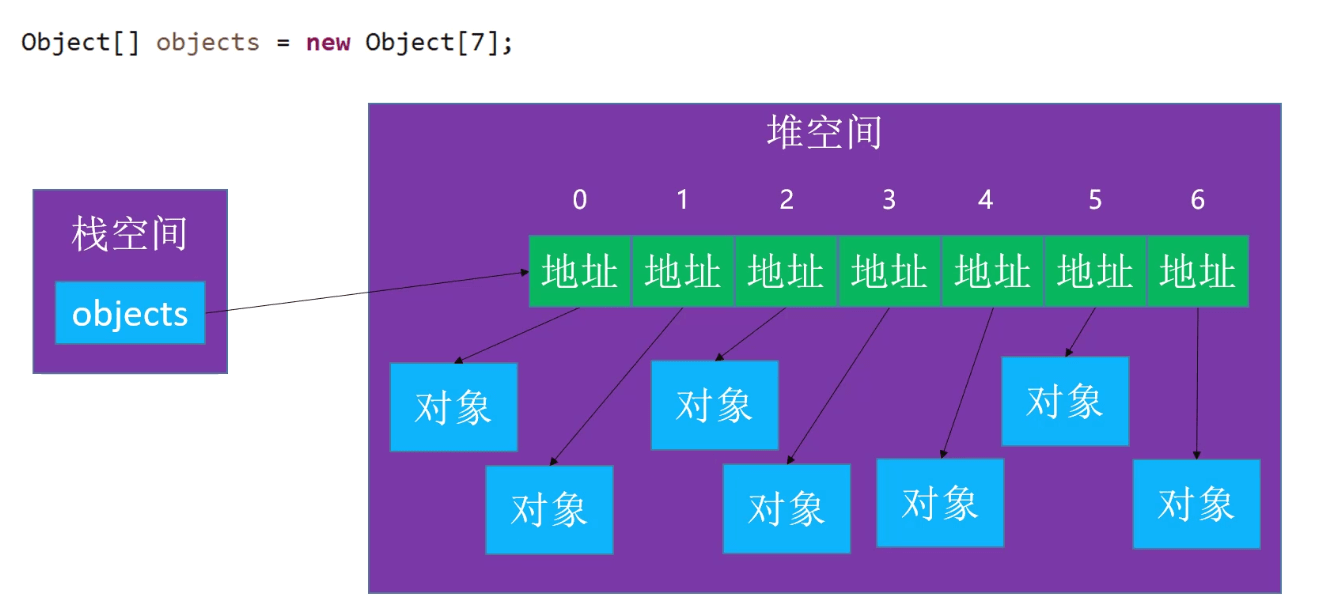
image.png

clear细节
如果像存int类型那样直接把size=0,是行不通的，因为这样清空之后继续add，原来的对象还是存在的，占内存的，会导致浪费内存。

  1. /**
  2. *清除所有元素
  3. */
  4. public void clear(){
  5.      for(int i=0;i<size;i++){
  6.          elements[i]=null;
  7.      }
  8.     size=0;
  9. }

直接设置为空，jvm会销毁对象

remove需要注意的细节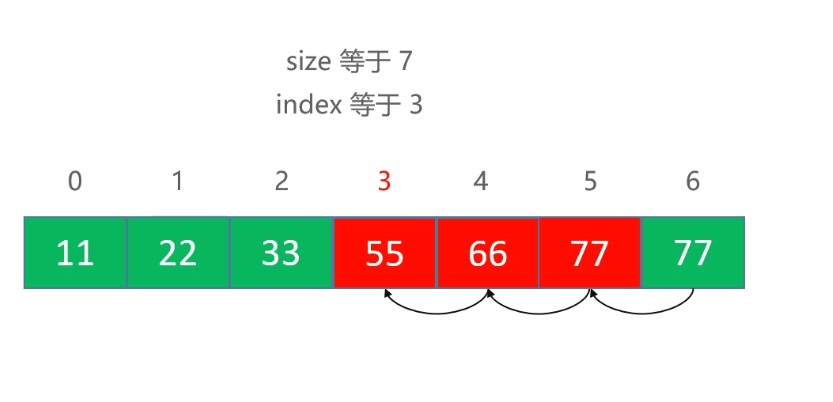
image.png
remove位置的值不需要清空，直接被后面的值覆盖，但是最后一个元素必须要清空，因为引用还存在

  1. public E remove(int index) {
  2.         rangCheck(index);
  3.         E old=elements[index];
  4.         for (int i = index; i < size - 1; i++) {
  5.             elements[i] = elements[i + 1];
  6.         }
  7.         elements[--size]=null;//必须要清空最后一个
  8.         return old;
  9.     }

关于equals方法
比较的时候要注意用equals方法

  1.   /**
  2.      * 查看元素的索引
  3.      *
  4.      * @param element
  5.      * @return
  6.      */
  7.     public int indexOf(E element) {
  8.         for (int i = 0; i < elements.length; i++) {
  9.             if (elements[i].equals(element)) return i;
  10.         }
  11.         return ELEMENT_NOT_FOUND;
  12.     }

null值的处理
添加的方法不用处理
indexof方法需要改变:

  1. public int indexOf(E element) {
  2.     if(){
  3.     }
  4.         for (int i = 0; i < elements.length; i++) {
  5.             if (elements[i].equals(element)) return i;
  6.         }
  7.         return ELEMENT_NOT_FOUND;
  8.     }

ArrayList源码分析
~

3.链表

1.简介
动态数组有一个明显的缺点，扩容的时候会导致内存浪费，导致很多内存用不上、
链表可以办到这一点，用多少内存就申请多少内存
链表是一种链式存储的线性表，所有元素的内存地址不一定是连续的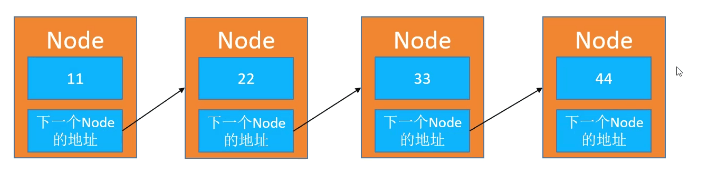
image.png

2.clear()清空元素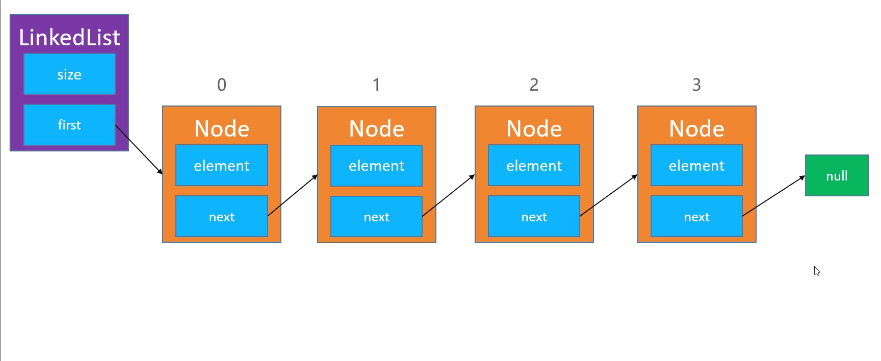
image.png
直接first=null，即可，让第一个节点为空，就无法继续寻找别的节点

3.添加元素

  1.    /**
  2.      * 从该索引插入一个元素
  3.      *
  4.      * @param index
  5.      * @param element
  6.      */
  7.     public void add(int index, E element) {
  8.         if (index == 0) {
  9.             first = new Node<>(element, first);
  10.         } else {
  11.             Node<E> prev = node(index - 1);
  12.             prev.next = new Node<>(element, prev.next);
  13.         }
  14.         size++;
  15.     }
  16.   /**
  17.      * 从后面插入一个元素
  18.      *
  19.      * @param element
  20.      */
  21.     public void add(E element) {
  22. //        Node<E> node = node(size - 1);//获取最后一个元素
  23. //        node.next = new Node<>(element, null);
  24.         add(size,element);
  25.     }

4.删除方法

  1.     /**
  2.      * 删除一个元素
  3.      * 返回被删掉的那个元素
  4.      * @param index
  5.      * @return  E
  6.      */
  7.     public E remove(int index) {
  8.         E old;
  9.         if (index == 0) {
  10.             old=first.element;
  11.             first = first.next;
  12.         } else {
  13.             Node<E> prev = node(index - 1);
  14.             old= prev.next.element;
  15.             prev.next = prev.next.next;
  16.         }
  17.         size--;
  18.         return old;
  19.     }

4.练习:删除链表中的节点_力扣:237题请编写一个函数，使其可以删除某个链表中给定的（非末尾）节点。传入函数的唯一参数为 要被删除的节点 。现有一个链表 — head = [4,5,1,9]，它可以表示为:4—->5—->1—->9示例 1：输入：head = [4,5,1,9], node = 5输出：[4,1,9]解释：给定你链表中值为5的第二个节点，那么在调用了你的函数之后，该链表应变为 4 -> 1 -> 9._

  1. public class Exercises {
  2.     public class ListNode {
  3.         int val;
  4.         ListNode next;
  6.         ListNode(int x) {
  7.             val = x;
  8.         }
  9.     }
  10.     class Solution {
  11.         public void deleteNode(ListNode node) {
  12.             node.val=node.next.val;
  13.             node.next=node.next.next;
  14.         }
  15.     }
  16. }

5.反转链表
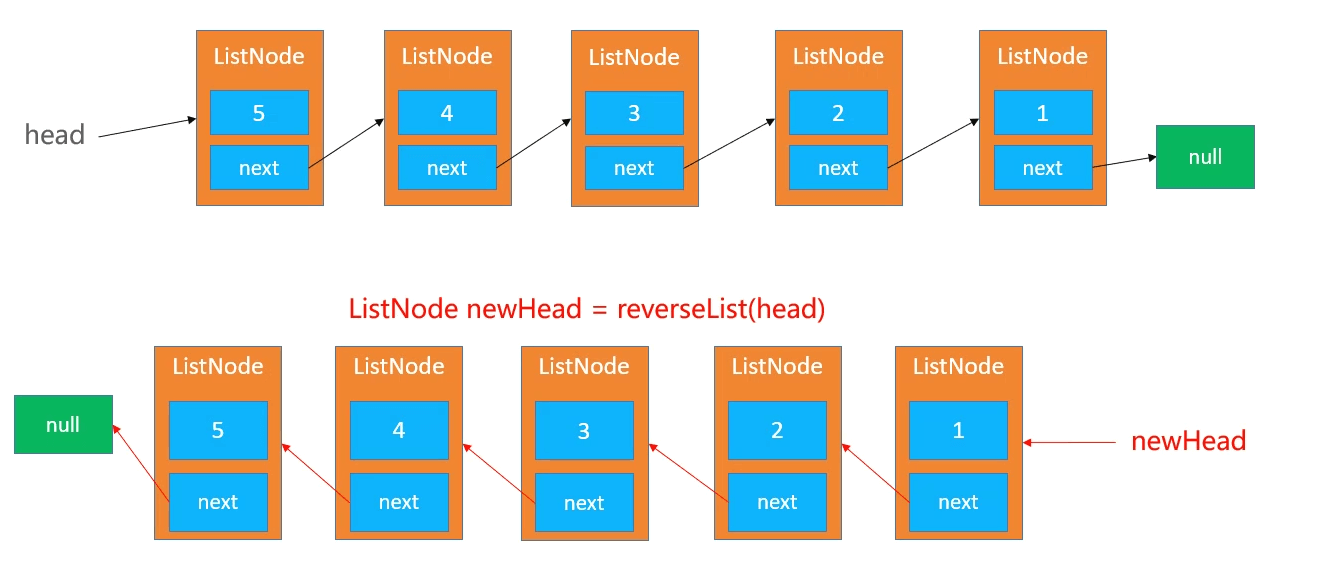
image.png
6.判断一个链表是否有环？

  1.  public boolean hasCycle(ListNode head) {
  2.         if (head == null || head.next == null) {
  3.             return false;
  4.         }
  5.         ListNode slow = head;
  6.         ListNode fast = head.next;
  7.         while (fast != null && fast.next != null) {
  8.             slow = slow.next;
  9.             fast = fast.next.next;
  10.             if (slow == fast) {
  11.                 return true;
  12.             }
  13.         }
  14.         return false;
  15.     }

注意fast != null && fast.next != null两个不能省略其中一个;
否则会报空指针异常；

7.虚拟头结点
有的时候为了让代码更加精简，统一所有节点的处理逻辑，可以考虑加一个虚拟头节点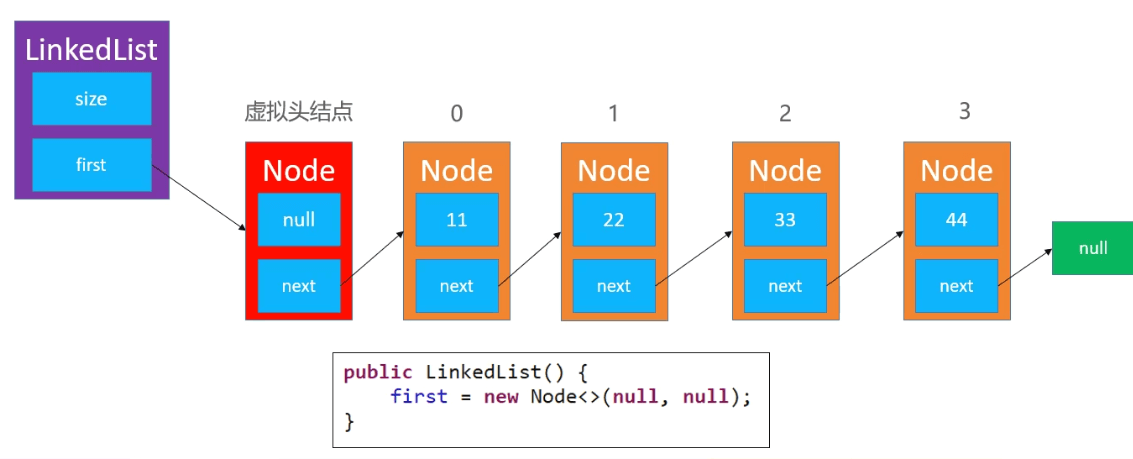
image.png
8.复杂度分析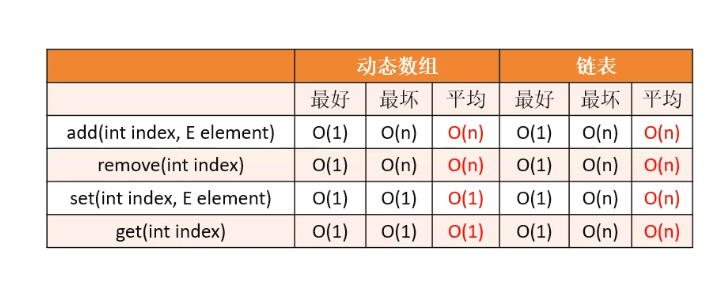
image.png

9.均摊复杂度
可以把扩容的那次操作的复杂度均摊到每次添加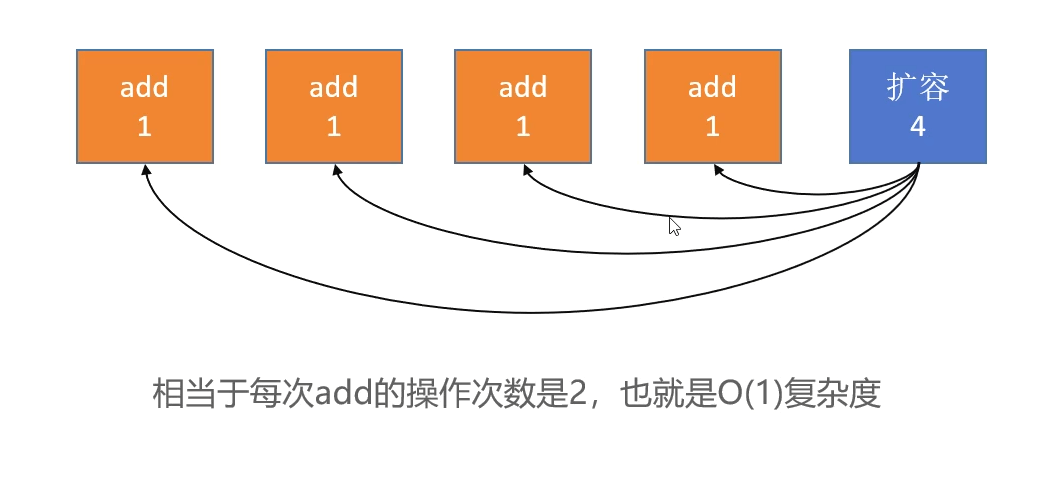
image.png
10.动态数组缩容
如果内存使用比较紧张，动态数组有比较多余的剩余空间，可以考虑进行缩容操作

  1.     /**
  2.      * 进行缩容操作
  3.      */
  4.     public void trim() {
  5.         int capacity = elements.length;
  6.         int newCapacity=capacity>>1;
  7.         if (size>=(capacity)||capacity<=DEFAULT_CAPACITY) {//如果移除后的数组长度大于一半,并且数组的长度小于初始长度,无需操作
  8.            return;
  9.         }
  10.         E[] newElements = (E[]) new Object[newCapacity];//新数组长度为原来的一半
  11.         for (int i = 0; i < size; i++) {
  12.             newElements[i] = elements[i];
  13.         }
  14.         elements = newElements;
  15.     }

复杂度震荡：
如果扩容倍数、缩容时机设计不得当，有可能会导致复杂度震荡
扩大倍数和缩小倍数不要一样，否则在临界点进行添加操作或者删除操作都会导致，频繁扩容和缩容

11.双向链表
使用双向链表可以提升链表的综合性能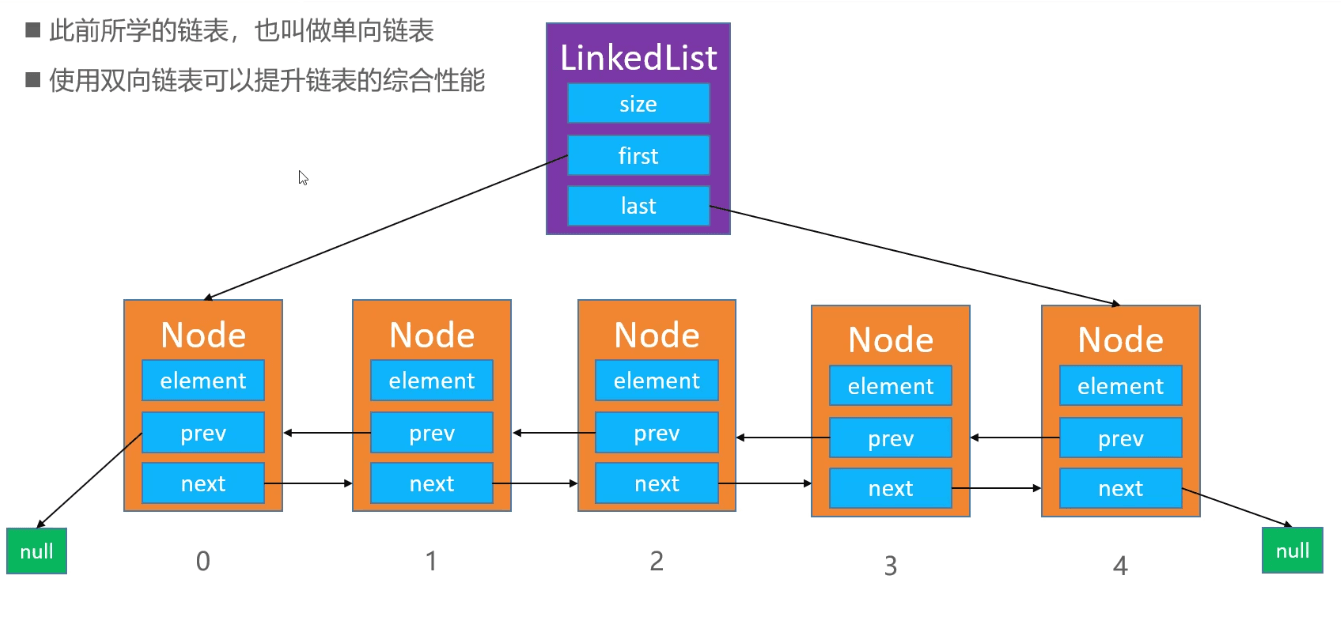
image.png
node方法:

  1.        /*
  2.        * 通过索引获得node节点*
  3.        */
  4.       private Node<E> node(int index) {
  5.             rangCheck(index);
  6.             if (index < (size >> 1)) { //如果索性小于长度的一半，就从头节点开始找
  7.                   Node<E> node = first;
  8.                   for (int i = 0; i < index; i++) {
  9.                         node = node.next;
  10.                   }
  11.                   return node;
  12.             } else {//如果索引大于长度的一半，就从尾节点开始找
  13.                   Node<E> node=last;
  14.                   for (int i = size-1; i > index; i--) {
  15.                    node=node.prev;
  16.                   }
  17.                   return node;
  18.             }
  19.       }

clear方法:

  1.  public void clear() {
  2.             size = 0;
  3.             first = null;
  4.             last = null;
  5.       }

问题：first和last原来所指向的对象会被虚拟机回收吗？
答案：会被回收，因为在虚拟机中没有被gc root所指向的引用都会被回收，比如被局部变量指向的对象就是，list就是被局部变量指向的对象 first<—-linkedlist—->last

add方法：
注意：
如果插入的点是0索引，则前面的结点为空
如果插入的是最后的索引，则后面的结点为空

  1. public void add(int index, E element) {
  2.         if (index == size) {//如果插入的索引等于长度,则表示插入的是最后一个位置
  3.             Node<E> prev =last;
  4.             last = new Node<>(element, prev, null);
  5.             prev.next=last;
  6.         } else {
  7.             Node<E> next = node(index);//获取当前元素
  8.             Node<E> prev = next.prev;//获取前一个元素
  9.             Node<E> newNode = new Node<E>(element, prev, next);
  10.             next.prev = newNode;
  11.             if (prev == null) {//如果当前结点的前一个节点为null,则表示插入的结点为0结点
  12.                 first = newNode;
  13.             } else {
  14.                 prev.next = newNode;
  15.             }
  16.         }
  17.     }

remove方法：
注意：跟add方法有点相似
如果插入的点是0索引，则前面的结点为空
如果插入的是最后的索引，则后面的结点为空

  1.     public void remove(int index) {
  2.             Node<E> node = node(index);
  3.             Node<E> next = node.next;
  4.             Node<E> prev = node.prev;
  5.             if (prev == null) {
  6.                 first = next;
  7.             } else {
  8.                 prev.next = next;
  9.             }
  10.             if(next==null){
  11.                 last = prev;
  12.             }else {
  13.                 next.prev = prev;
  14.             }
  15.            size--;
  16.     }

12.总结
单向链表vs双向链表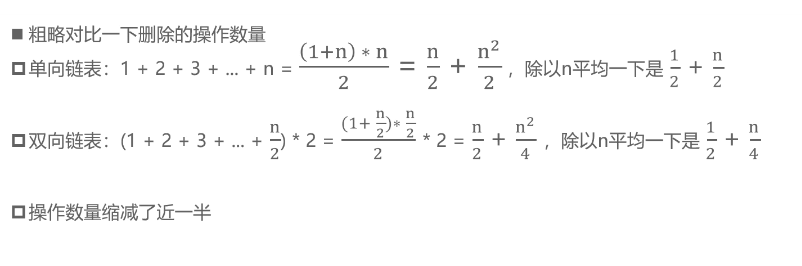
image.png
双向链表vs动态数组
动态数组：开辟、销毁内存空间的次数相对较少，但可能造成内存空间浪费(可以通过缩容解决)
双向链表：开辟、销毁内存空间的次数相对较多，但不会造成内存空间的浪费

如果频繁在尾部进行添加、删除操作，动态数组、双向链表均可选择
如果频繁在头部进行添加、删除操作，建议选择使用双向链表
如果有频繁的(在任意位置添加)添加、删除操作，建议使用双向链表
如果有频繁的查询操作(随机访问操作)，建议选择使用动态数组

有了双向链表，单向链表是否就没有任何作用了？
并非如此，在哈希表的设计中就用到了双链表

13.源码分析
在源码中的删除代码是把每个节点都清空
因为在源码中有用到迭代器，迭代器引用某个结点的话会导致内存不会被回收

14.单向循环链表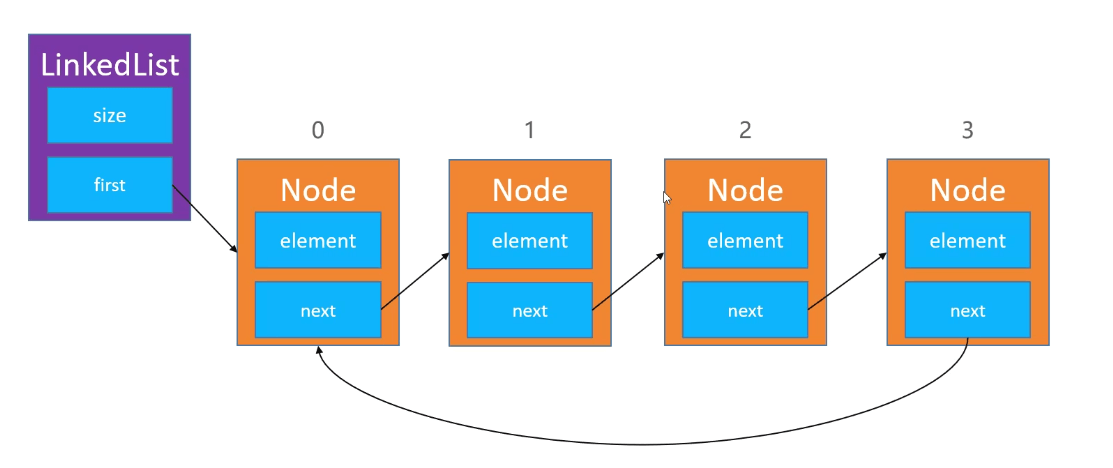
image.png

15.双向循环链表
只需要修改添加和修改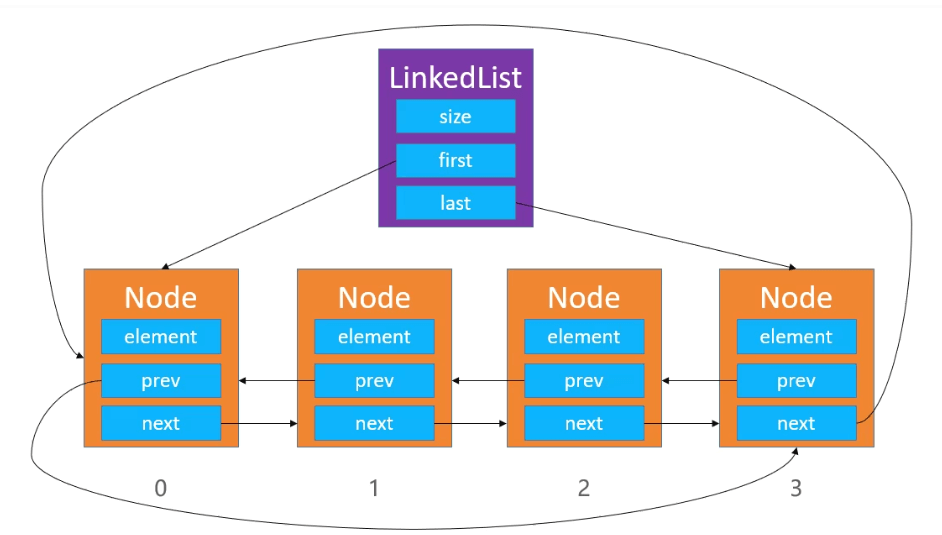
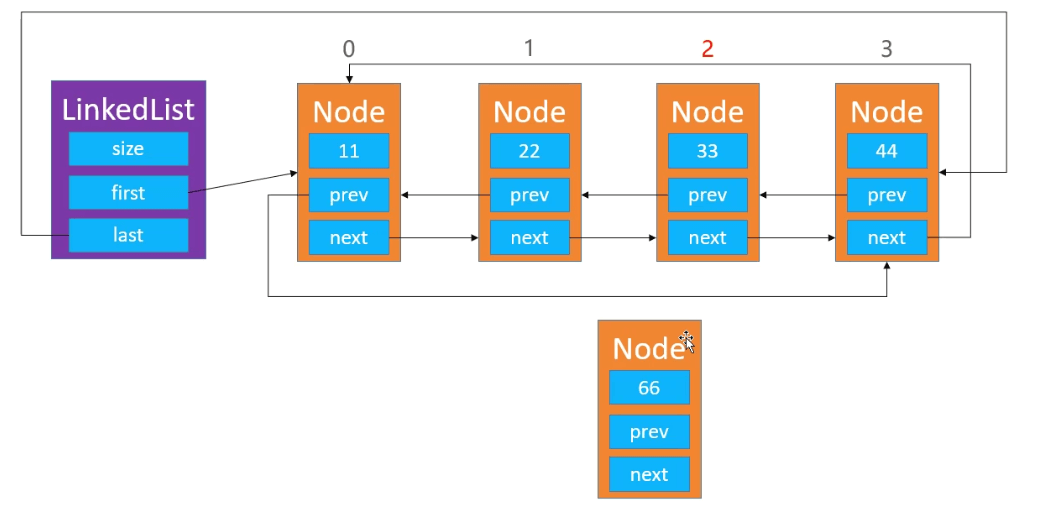
image.png

image.png
双向循环链表如果只有一个结点，那么他会自己指向自己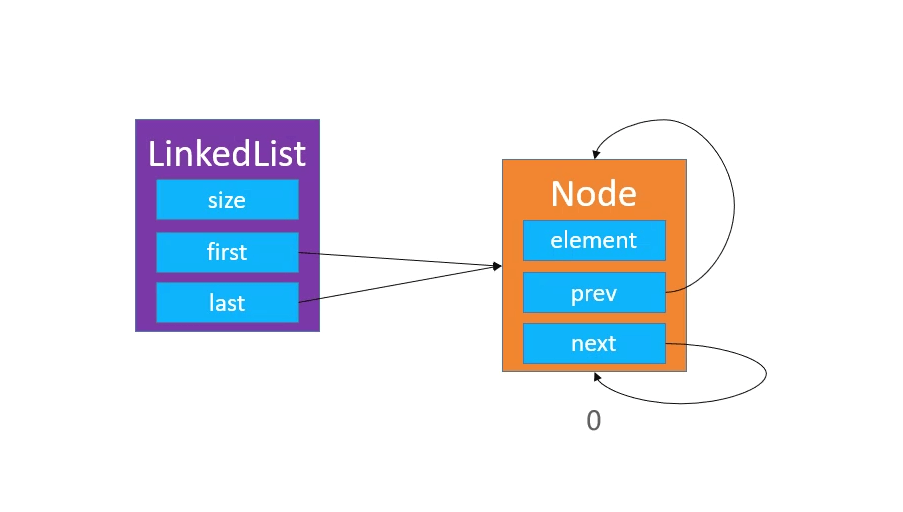
image.png
add方法:
需要注意的点：环形链表只有一个结点

  1.     public void add(int index, E element) {
  2.         if (index == size) {//如果插入的索引等于长度,则表示插入的是最后一个位置,即从最后面添加
  3.             Node<E> oldNode =last;
  4.             last = new Node<>(element, oldNode, first);//新增的节点
  5.             if(oldNode==null){   //说明这个链表是空链表
  6.                 first=last;
  7.                 last.next=last;
  8.                 last.prev=last;
  9.             }else {//说明不是空链表
  10.                 oldNode.next=last;
  11.                 last.next=first;
  12.             }
  13.         } else {
  14.             Node<E> next = node(index);//获取当前元素
  15.             Node<E> prev = next.prev;//获取前一个元素
  16.             Node<E> newNode = new Node<E>(element, prev, next);
  17.             next.prev = newNode;
  18.             if (prev == null) {//如果当前结点的前一个节点为null,则表示插入的结点为0结点
  19.                 first = newNode;
  20.             } else {
  21.                 prev.next = newNode;
  22.             }
  24.         }
  25.         size++;
  26.     }

remove方法：
理解:因为环形链表是一个环，只有一个元素的时候需要特殊考虑，别的情况都是一样，头尾结点只需要指明头尾结点即可

  1.     public E remove(int index) {//至少有一个元素
  2.         Node<E> node = node(index);
  3.         Node<E> next = node.next;
  4.         Node<E> prev = node.prev;
  5.         if (size == 1) {
  6.             first = null;
  7.             last = null;
  8.         } else {
  9.             prev.next = next;
  10.             next.prev = prev;
  11.             if (node == first) {//则代表这是第一个元素
  12.                 first = next;
  13.             }
  14.             if (node.next == first) {//则代表这是最后一个元素
  15.                 last = prev;
  16.             }
  17.         }
  18.         size--;
  19.         return node.element;
  20.     }
  1.                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                     <br />**16.约瑟夫问题：**<br />![image.png](https://cdn.nlark.com/yuque/0/2021/png/301083/1622125869594-8e3d0619-6e9d-42af-9a3f-73d5b5c4ec39.png#crop=0&crop=0&crop=1&crop=1&height=374&id=X4OcA&margin=%5Bobject%20Object%5D&name=image.png&originHeight=499&originWidth=932&originalType=binary&ratio=1&rotation=0&showTitle=false&size=132510&status=done&style=none&title=&width=699)<br />如何发挥出循环链表的最大威力？<br />可以考虑增设一个成员变量、三个方法<br />current：用于指向某个节点<br />void  reset()：让current指向头节点first<br />E  next()：让current往后走一步，也就是current=current.next<br />E  remove()：删除current指向的节点，删除成功后让current指向下一个节点

17.静态链表
前面所学的链表，是依赖于指针(引用)实现的
有些编程语言是没有指针的，比如早期的BASIC、FORTRAN语言
在没有指针的情况下，如何实现链表？
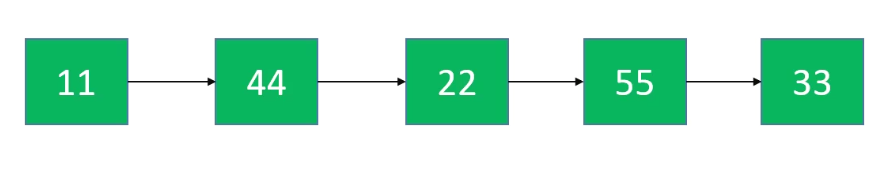
可以通过数组来模拟链表，称为静态链表
数组的每个元素存放2个数据：值、下个元素的索引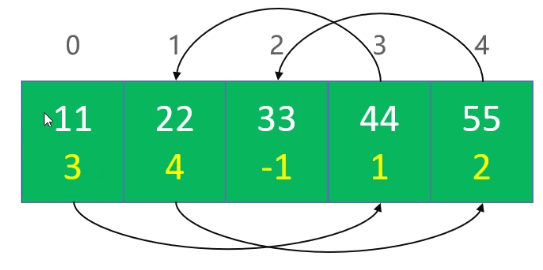
image.png
image.png
18.ArrayList优化

4.栈

1.设计和实现
栈是一种特殊的线性表，只能在一端进行操作
往栈中添加元素的操作，一般叫做push,入栈
从栈中移除元素的操作，一般叫做pop,出栈(只能移除栈顶元素，也叫做：弹出栈顶元素)
后进先出的原则，Last In First Out ,LIFO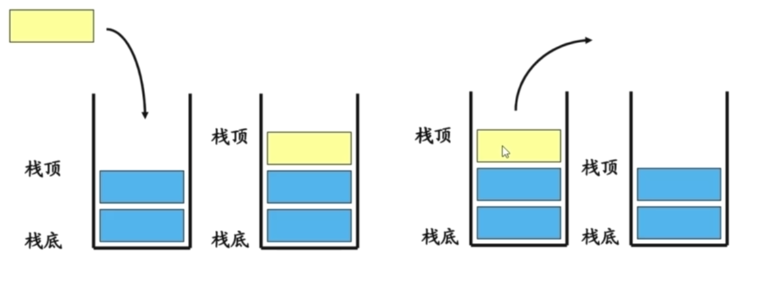
image.png
注意:这里说的”栈”与内存中的”栈空间”是两个不同的概念

image.png
image.png
栈的内部实现是否可以直接利用以前学过的数据结构？
动态数组、链表

栈的实现

  1. package com.ruoyi.Algorithms.f4栈;
  3. import java.util.ArrayList;
  4. import java.util.List;
  6. public class Stack1<E> {
  7.     private List<E> list=new ArrayList<E>();
  8.     /**
  9.      * 入栈操作
  10.      * @param element
  11.      */
  12.     public void push(E element){
  13.         list.add(element);
  14.     }
  16.     /**
  17.      * 出栈操作
  18.      * @return
  19.      */
  20.     public E pop(){
  21.         return list.remove(list.size()-1);
  22.     }
  24.     /**
  25.      * 获取栈顶的元素
  26.      * @return
  27.      */
  28.     public E top(){
  29.         return list.get(list.size() - 1);
  30.     }
  32.     /**
  33.      * 判断是否为空
  34.      * @return
  35.      */
  36.     public boolean isEmpty(){
  37.        return list.isEmpty();
  38.     }
  39. }

2.栈的应用
浏览器的前进和后退

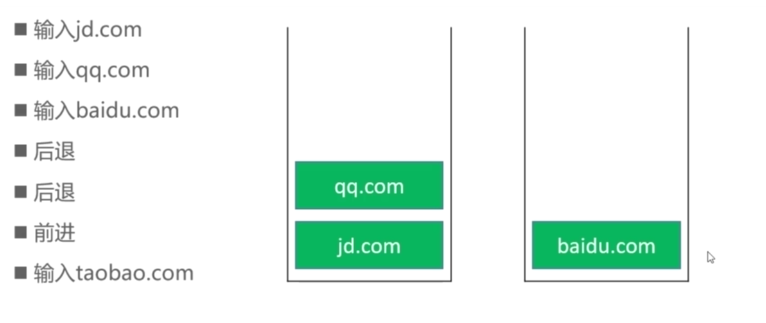
image.png
前进：左边栈顶元素弹出右边
后退：右边栈元素弹出左边
输入网址跳转，往左边栈顶加元素，清空右边栈
类似的应用场景：
软件的撤销、恢复功能

3.有效的括号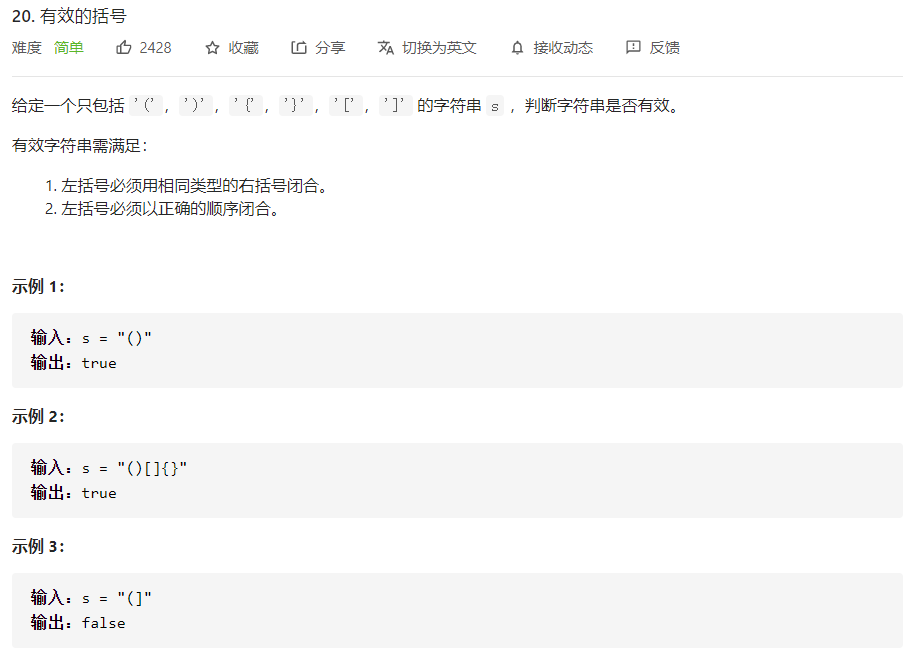
image.png
方法一：直接使用字符串操作替换，容易想到，但是效率非常低，因为String还是不可变的字符串，适合新手

  1. class Solution {
  2.     public boolean isValid(String s) {
  3.         while(s.contains("()")||s.contains("{}")||s.contains("[]")){
  4.             s.replace("{}","");
  5.             s.replace("[]","");
  6.             s.replace("()","");
  7.         }
  8.       return s.isEmpty();
  9.     }
  10. }

方法二：直接使用栈

  1. public boolean isValid(String s){
  2.         java.util.Stack<Character> stack=new java.util.Stack<Character>();
  3.         int len=s.length();
  4.         for (int i = 0; i < len; i++) {
  5.             char c=s.charAt(i);
  6.             //如果是左边括号的话,就进行入栈操作
  7.             if(c=='('||c=='{'||c=='['){
  8.               stack.push(c);
  9.             }else {
  10.               if(stack.isEmpty()){
  11.                 return false;
  12.               }
  13.               char left = stack.pop();
  14.               if(left=='('&& c!=')') return false;
  15.               if(left=='['&& c!=']') return false;
  16.               if(left=='{'&& c!='}') return false;
  17.             }
  18.         }
  19.         return stack.isEmpty();
  20.     }

clear方法: list.clear()即可

6.二叉树

1.树的基本概念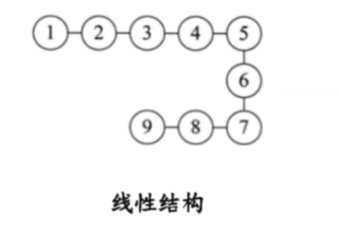
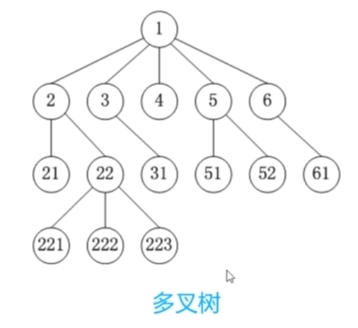
image.png
image.pngimage.png
节点、根节点、父节点、子节点、兄弟节点
一棵树没有任何节点，成为空树
一颗树可以只有一个节点，也就是只有根节点
子树、左子树、右子树

节点的度：子树的个数
树的度：所有节点度中的最大值
叶子节点：度为0的节点
非叶子节点：度不为0的节点
层数：根节点在第1层，根节点的子节点在第2层，以此类推(有些教程也从第0层开始计算)
节点的深度：从根节点到当前节点的唯一路径
节点的高度：从当前节点到最远叶子节点的路径上的节点总数
树的深度：所有节点深度中的最大值
树的高度：所有节点高度中的最大值
树的深度等于树的高度

有序树：树中任意节点的子节点之间有顺序关系
无序树：树中任意节点的子节点之间没有顺序关系
森林：由m(m>=0)颗互不相交的树组成的集合

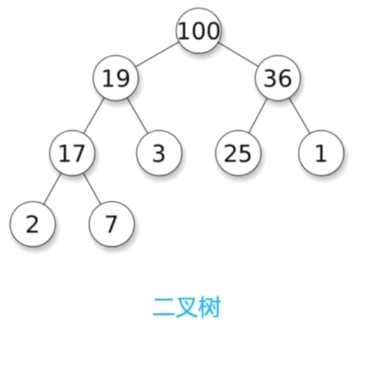
2.二叉树
每个节点的度最大为2(最多拥有2颗子树)
左子树和右子树是有顺序的
即使某节点只有一颗子树，也要区分左右子树
二叉树是有序树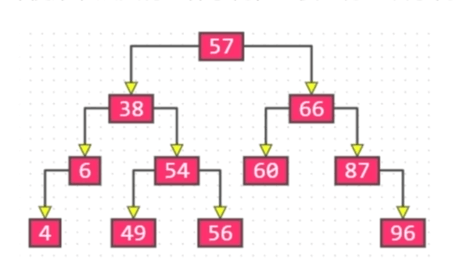
image.png
二叉树的性质:
非空二叉树的第i层，最多有2^(i-1) 个节点 (i>=1)
在高度为h的二叉树上最多有2^(h-1)个结点 (h>=1)
对于任何一颗非空二叉树，如果叶子节点个数为n0，度为2的节点个数为n2，则有：n0=n2+1
假设度为1的节点个数为n1，那么二叉树的节点总数n=n0+n1+n2
二叉树的边数T=n1+2*n2=n-1=n0+n1+n2-1

3.真二叉树、满二叉树
真二叉树：所有的节点的度都要么为0，要么为2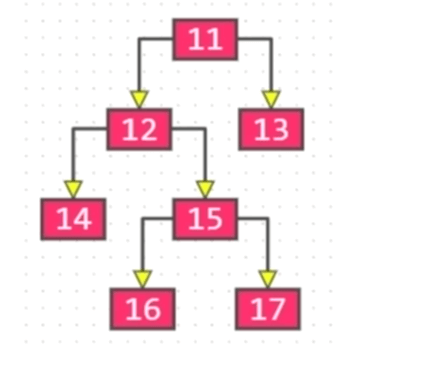
image.png
满二叉树：所有的节点的度要么为0，要么为2。且所有的叶子节点都在最后一层

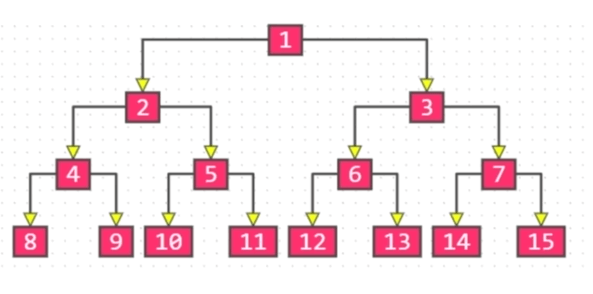
image.png
同样高度的二叉树中，满二叉树的叶子节点数量最多、总节点数量最多
满二叉树一定是真二叉树，真二叉树不一定是满二叉树
假设满二叉树的高度为h (h>=1),那么
第 i 层的节点数量：2^(i-1)
叶子节点数量2^(h-1)
总节点数量n
n=2^h-1=2^0+2^1+…+2^(h-1)
h=log2(n+1)

完全二叉树
叶子节点只会出现在最后两层，且最后一层的叶子节点都靠左对齐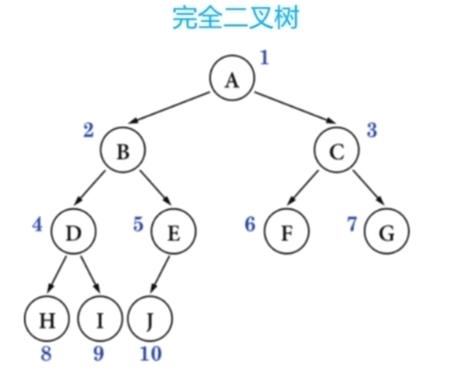
image.png
完全二叉树从根节点到倒数第二层是满二叉树
满二叉树一定是完全二叉树
性质:
度为1的节点只有左子树
度为1的节点要么是1个，要么是0个
同样节点数量的二叉树，完全二叉树的高度最小
假设完全二叉树的高度为h(h>=1)，那么
1.至少有2^(h-1)个节点(2^0+2^1+2^2+…+2^(h-2) +1)
2.最多有(2^h)-1个节点(2^0+2^1+2^2+…+2^(h-1),满二叉树)0
假设总节点数量为n，求高度
2^(h-1)<=n<2^h
h-1<=log(2^n)<h
h=floor(log2n)+1
floor是向下取整，ceiling是向上取整

一颗有n个节点的完全二叉树(n>0),从上到下，从左到右对节点从1开始进行编号，对任意第i个节点
如果 i=1，它是根节点
如果 i>1,它的父节点编号为 floor(i/2)
如果 2i<=n,它的左子节点编号为 2i
如果 2i>n，它无左子节点
如果 2i+1<=n ,它的右子节点编号为2i+1

面试题：如果一颗完全二叉树有768个节点，求叶子节点的个数
假设叶子节点的个数为能n0,度为1的节点个数为n1，度为2的节点个数为n2
总结点个数n=n0+n1+n2 , 而且n0 = n2+1
n=2n0+n1-1
完全二叉树的n1要么为0，要么为1
n1为1时，n=2n0 ,n必然是偶数
叶子节点个数n0=n/2,非叶子节点个数n1+n2=n/2
n1=0时，n=2n0-1,n必然是奇数
叶子节点个数n0=(n+1)/2,非叶子节点个数n1+n2=(n-1)/2

通用公式:n0=floor（(n+1)/2）

7.二叉搜索树

二叉搜索树是二叉树的一种，是应用非常广泛的一种二叉树，英文简称BST
又被成为：二叉查找树、二叉排序树
任意一个节点的值都大于其左子树所有节点的值
任意一个节点的值都小于其右子树所有节点的值
它的左右子树也是一颗二叉搜索树
二叉搜索树可以大大提高搜索数据的效率

二叉搜索树存储的元素必须具备可比较性
比如int、double等
如果是自定义类型，需要指定比较方式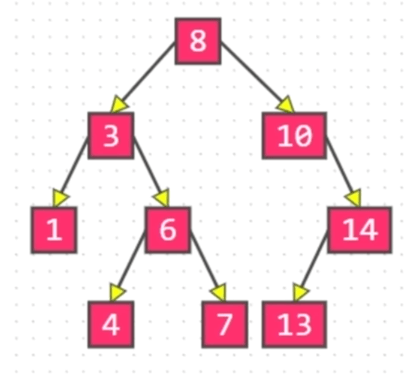
image.png

二叉搜索树的接口
int size() //元素的数量
boolean isEmpty() //是否为空
void clear() //请空所有元素
void add(E element) //添加元素
void remove(E element) //删除元素
boolean contains(E element) //是否包含某种元素

需要注意的是
对于我们现在使用的二叉树来说，它的元素没有索引的概念
为什么?

基本实现:

  1. package com.ruoyi.Algorithms.f5二叉搜索树;
  4. public class BinarySearchTree<E> {
  6.     private int size;//长度
  7.     private Node<E> root;//根节点属性
  9.     private static class Node<E> {
  10.         E element;
  11.         Node<E> left;
  12.         Node<E> right;
  13.         Node<E> parent;
  15.         public Node(E element, Node<E> parent) {
  16.             this.element = element;
  17.             this.parent = parent;
  18.         }
  19.     }
  21.     //判断节点是否为null
  22.     private void elementNotNullCheck(E element) {
  23.         if (element == null) {
  24.             throw new IllegalArgumentException("element must not be null");
  25.         }
  26.     }
  28.     //元素的数量
  29.     public int size() {
  30.         return 0;
  31.     }
  33.     //是否为空
  34.     public boolean isEmpty() {
  35.         return false;
  36.     }
  38.     //请空所有元素
  39.     public void clear() {
  41.     }
  43.     //添加元素
  44.     public void add(E element) {
  45.     }
  47.     //移除元素
  48.     public void remove(E element) {
  49.     }
  51.     //是否包含某种元素
  52.     public boolean contains(E element) {
  53.         return false;
  54.     }
  55. }

add方法实现：
先找到父节点，然后再进行操作

  1. //添加元素
  2.     public void add(E element) {
  3.         elementNotNullCheck(element);
  4.         //添加第一个节点
  5.         if (root == null) {
  6.             root = new Node<>(element, null);
  7.             size++;
  8.             return;
  9.         }
  10.         //添加不是第一个节点
  11.         //找到父节点
  12.         Node<E> parent=null;
  13.         Node<E> node = root;
  14.         int cmp=0;
  15.         while (node != null) {
  16.             //跟节点比较
  17.             cmp = compare(element, node.element);
  18.             parent=node;
  19.             if (cmp > 0) {
  20.                 node = node.right;
  21.             } else if (cmp < 0) {
  22.                 node = node.left;
  23.             } else {
  24.                 return;
  26.             }
  27.         }
  29.         //看看插入到父节点的哪个位置
  30.         Node<E> newNode=new Node<>(element,parent);
  31.         if(cmp>0){
  32.            parent.right=newNode;
  33.         }else {
  34.            parent.left=newNode;
  35.         }
  36.         size++;
  37.     }

比较器方法:
在二叉搜索树中的元素必须是可比较的，所有必须要传入比较器或者实现比较器

  1. public class BinarySearchTree<E> {  
  2. private int size;//长度
  3.     private Node<E> root;//根节点属性
  4.     private Comparator<E> comparator;
  6.     public BinarySearchTree() {
  7.         this(null);
  8.     }
  10.     public BinarySearchTree(Comparator<E> comparator) {
  11.         this.comparator = comparator;
  12.     }
  13. public int compare(E element1, E element2) {
  14.         if(comparator!=null){
  15.             return comparator.compare(element1,element2);
  16.         }
  17.         return ((Comparable<E>)element1).compareTo(element2);
  18.     }
  19. }
  20.  public static void main(String[] args) {
  21.         //像Integer这些都是默认有比较器的
  22.         BinarySearchTree binarySearchTree=new BinarySearchTree<Person>(Comparator.comparingInt(Person::getAge));
  23.         binarySearchTree.add(new Person("何华宇",15));
  24.     }

未完待续…

8.B树

初识红黑树: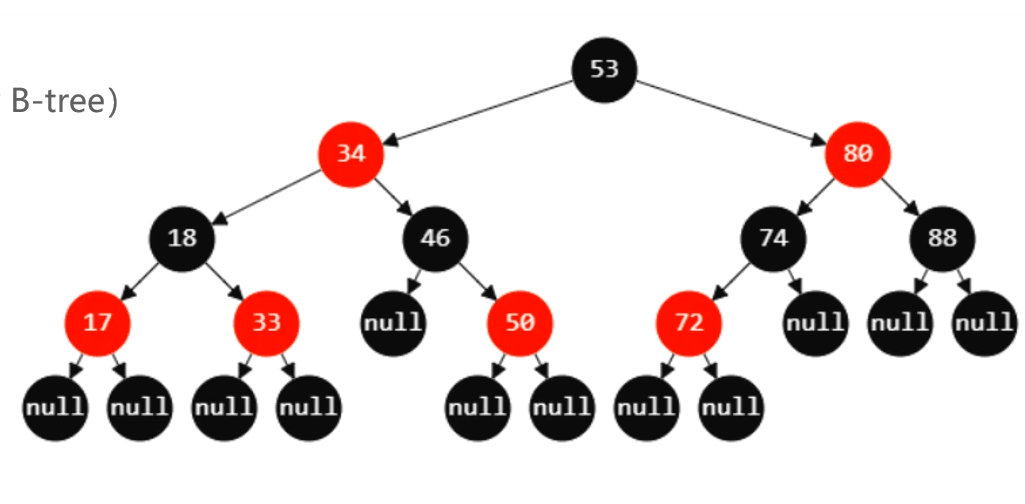
image.png
红黑树是一种自平衡二叉搜索树
以前也叫做平衡二叉B树
红黑树必须满足以下5个性质
1.节点是RED或者BLACK
2.根节点是BLACK
3.叶子节点(外部节点,空节点)都是BLACK
4.RED节点的子节点都是BLACK
RED节点的parent都是BLACK
从根节点到叶子节点的所有路径上不能有2个连续的RED节点
5.从任一节点到叶子节点的所有路径都包含相同数目的BLACK节点

B树(B-tree,b-树):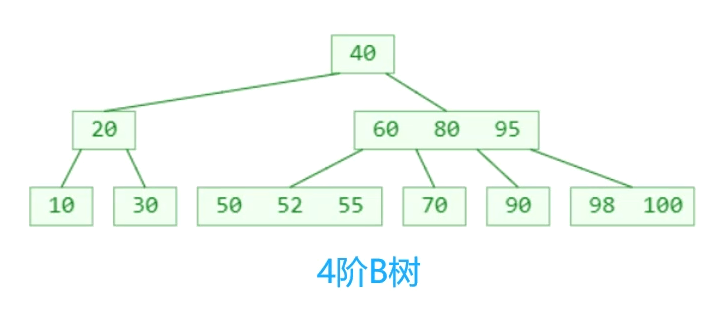
image.png
B树是一种平衡的多路搜索树,多用于文件系统,数据库的实现
仔细观察B树,有什么眼前一亮的特点?
1个节点可以存储超过2个元素,可以拥有超过2个子节点
拥有二叉搜索树的一些性质
平衡,每个节点的所有子树高度一致
比较矮

m阶B树的性质(m>=2)
阶数怎么区分:一个节点最多拥有的节点数称为阶数
假设一个节点存储的元素个数为X
根节点:1<=x<=m-1;

非根节点: ⌈m/2 ⌉ -1 <= x <= m-1;

如果有子节点,子节点个数y=x+1;
1)根节点:2<=y<=m
2)非根节点:⌈m/2 ⌉ -1<=y<=m,
比如m=3, 2<=y<=3, 因此可以称为(2,3)树,2-3树
比如m=4,2<=y<=4,因此可以称为(2,4)树,2-3-4树
以此类推

B树和二叉搜索树的区别: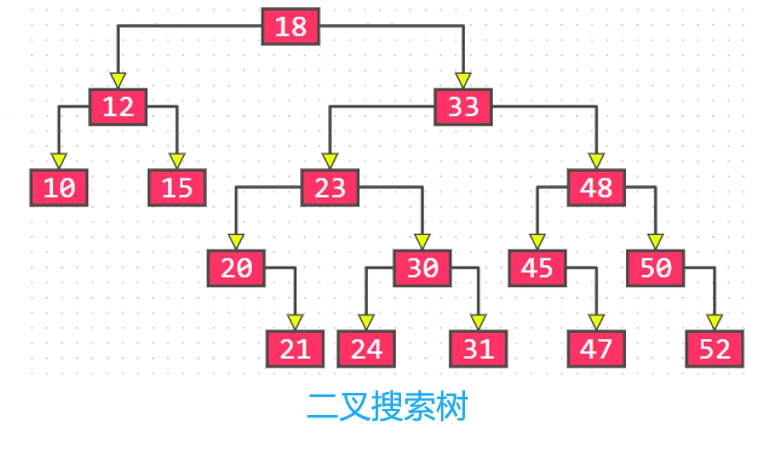
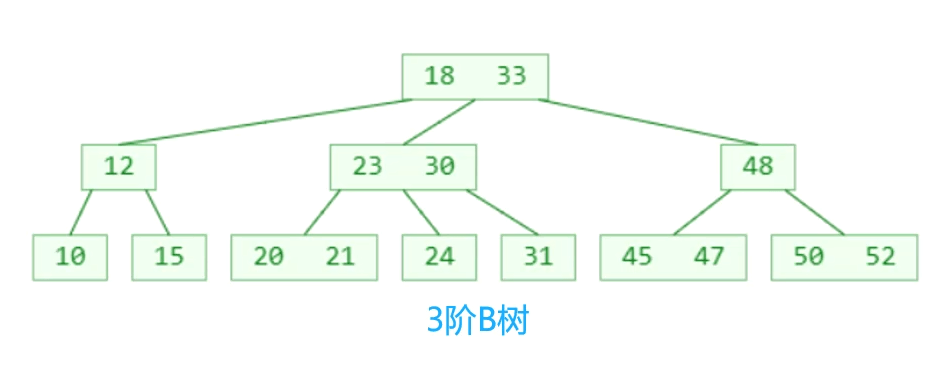
image.png

image.png
B树和二叉搜索树,在逻辑上是等价的
多代节点合并,可以获得一个超级节点
2代合并的超级节点,最多拥有4个子节点(至少是4阶B树)
3代合并的超级节点,最多拥有8个子节点(至少是8阶B树)
n代合并的超级节点,最多拥有2^n个子节点(至少是2^n阶B树)

m阶段B树,最多需要log2(m)代合并

搜索:
1.先在节点内部从小到大开始搜索元素
2.如果命中,搜索结束
3.如果未命中,再去对应的子节点中搜索元素,重复步骤1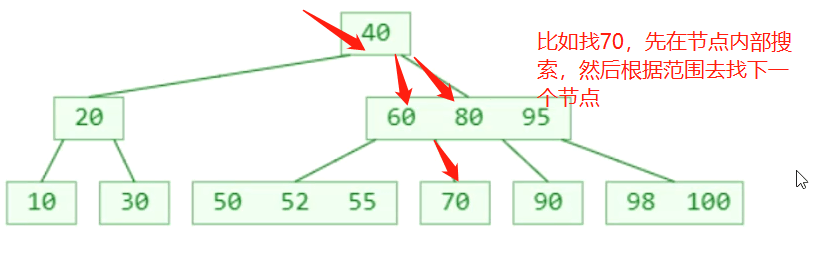
image.png
添加:
新添加的元素必定是添加到叶子节点
image.png