概念

单调队列是指：队列中元素之间的关系具有单调性，而且，队首和队尾都可以进行出队操作，只有队尾可以进行入队操作。

而这个队列的单调性就是指，所有在队列里的数都必须按照递增（或递减）的顺序列队，如果真有这么一个队列，那么队列的头就是该队列中的最小（或最大）值。

用单调队列来解决的问题一般都是：需要得到当前某个范围内的最小值或最大值。

实际生活中也有单调队列的例子：

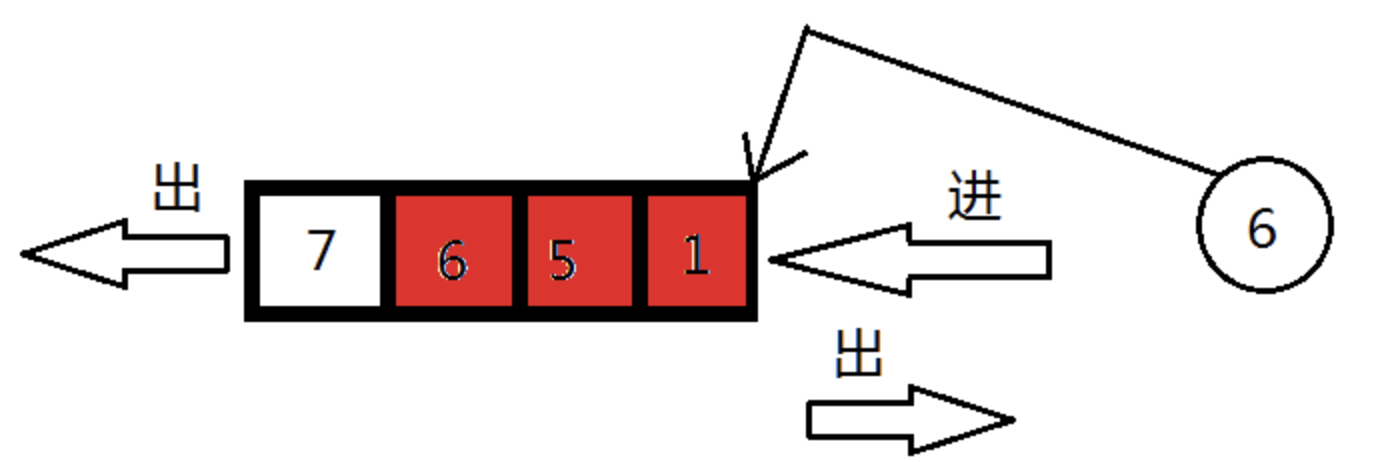
假如你在食堂打饭，有个人人高马大，急匆匆跑过来，看排了这么一长串队，心中急躁，从队列的最后一个开始，看见好欺负的就赶走，自己站着，直到干不过就停下，这就是双端队列。也就是允许两端弹出，只允许一端插入的队列（允许两端插入，只允许一端弹出的也属于双端队列）。这个人的插队行为类似于下面这幅图。

image.png

经典使用

题目：LC239.滑动窗口最大值

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回滑动窗口中的最大值。

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置 最大值
————————— ——-
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7

输入：nums = [1,-1], k = 1
输出：[1,-1]

输入：nums = [9,11], k = 2
输出：[11]

滑动窗口最大值.gif

  1. var maxSlidingWindow = function (nums, k) {
  2.     //单调队列数组，存放的是元素的下标，为了取值方便(存放窗口中值的下标)
  3.     const queue = [];
  4.     // 结果数组
  5.     const ans = [];
  6.     for (let i = 0; i < nums.length; i++) {
  7.         // 若队列有值 且 当前元素大于等于队尾所存下标的元素，则弹出队尾(当前元素>队尾元素，则弹出队列)
  8.         while (queue.length && nums[i] >= nums[queue[queue.length - 1]]) {
  9.             queue.pop();
  10.         }
  11.         // 入队 当前元素的下标
  12.         queue.push(i)
  13.         // 判断当前最大值（即队首元素）是否在窗口中，若不在便将其出队(队首值的下标大于i-k)
  14.         while (queue[0] <= i - k) {
  15.             queue.shift();
  16.         }
  17.         // 当达到窗口大小时便开始向结果中添加元素
  18.         if (i >= k - 1) ans.push(nums[queue[0]]);
  19.     }
  20.     return ans
  21. };
  23. console.log(maxSlidingWindow([1, 3, -1, -3, 5, 3, 6, 7], k = 3))

image.png

由于我们需要求出的是滑动窗口的最大值，如果当前的滑动窗口中有两个下标 ii 和 jj，其中 ii 在 jj 的左侧（i < ji<j），并且 ii 对应的元素不大于 jj 对应的元素（\textit{nums}[i] \leq \textit{nums}[j]nums[i]≤nums[j]），那么会发生什么呢？

当滑动窗口向右移动时，只要 ii 还在窗口中，那么 jj 一定也还在窗口中，这是 ii 在 jj 的左侧所保证的。因此，由于 \textit{nums}[j]nums[j] 的存在，\textit{nums}[i]nums[i] 一定不会是滑动窗口中的最大值了，我们可以将 \textit{nums}[i]nums[i] 永久地移除。

因此我们可以使用一个队列存储所有还没有被移除的下标。在队列中，这些下标按照从小到大的顺序被存储，并且它们在数组 \textit{nums}nums 中对应的值是严格单调递减的。因为如果队列中有两个相邻的下标，它们对应的值相等或者递增，那么令前者为 ii，后者为 jj，就对应了上面所说的情况，即 \textit{nums}[i]nums[i] 会被移除，这就产生了矛盾。

当滑动窗口向右移动时，我们需要把一个新的元素放入队列中。为了保持队列的性质，我们会不断地将新的元素与队尾的元素相比较，如果前者大于等于后者，那么队尾的元素就可以被永久地移除，我们将其弹出队列。我们需要不断地进行此项操作，直到队列为空或者新的元素小于队尾的元素。

由于队列中下标对应的元素是严格单调递减的，因此此时队首下标对应的元素就是滑动窗口中的最大值。但与方法一中相同的是，此时的最大值可能在滑动窗口左边界的左侧，并且随着窗口向右移动，它永远不可能出现在滑动窗口中了。因此我们还需要不断从队首弹出元素，直到队首元素在窗口中为止。

为了可以同时弹出队首和队尾的元素，我们需要使用双端队列。满足这种单调性的双端队列一般称作「单调队列」。