滑动窗口算法(Sliding Window Algorithm)
滑动窗口算法是给特定窗口大小的数组或字符串上执行要求的操作。
简而言之,滑动窗口算法在一个特定大小的字符串或者数组上进行操作,而不在整个字符串或者数组上操作,这样就降低了问题的复杂度,从而达到降低了循环的嵌套深度。其实这里就可以看出来滑动窗口算法主要应用在数组和字符串上。
算法思路
为了便于理解,以下采用的是字符串来讲解。但是对于数组其实也是一样的。
滑动窗口算法的思路是这样:
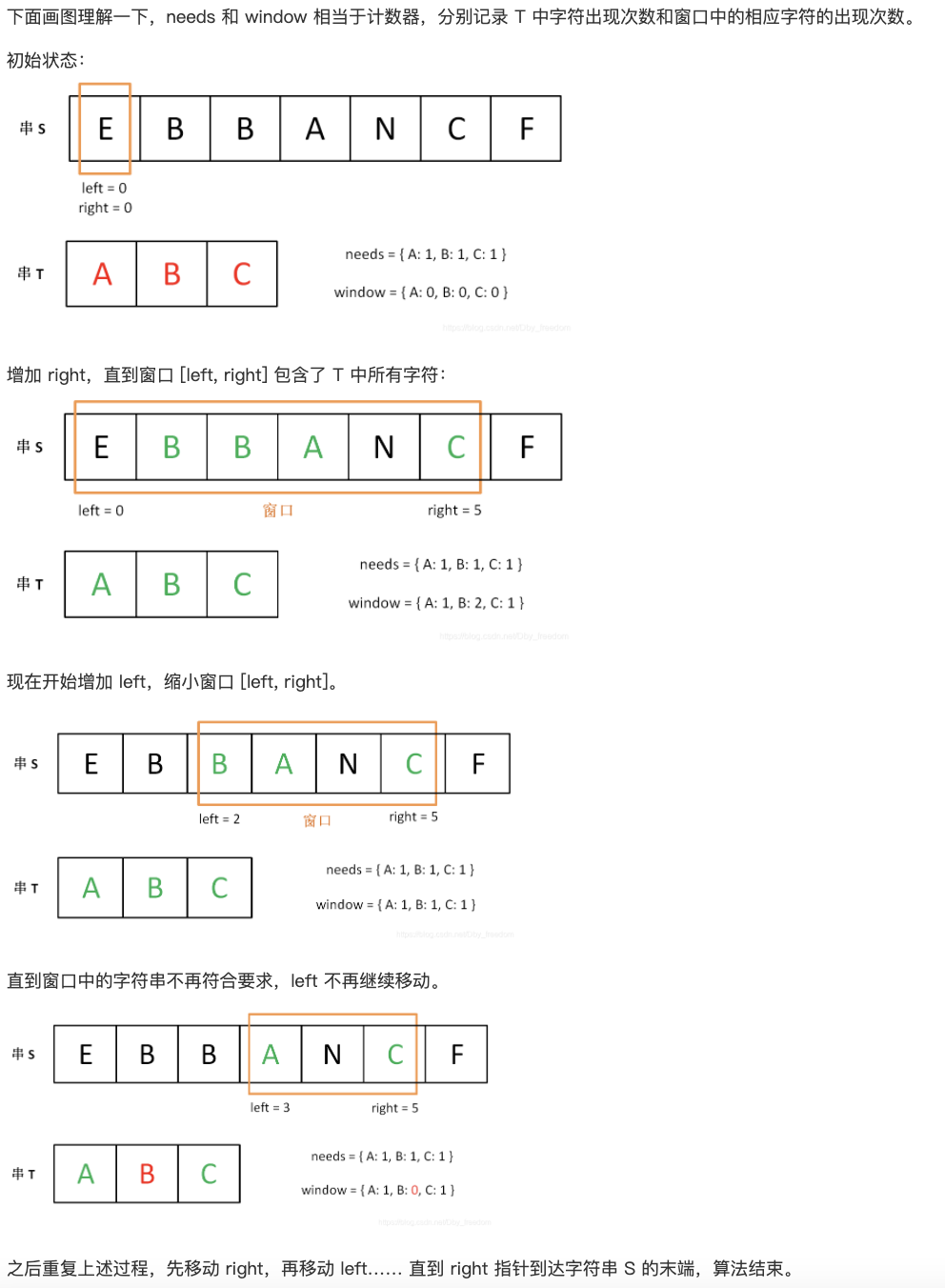
- 我们在字符串S中使用双指针中的左右指针技巧,初始化 left = right = 0,把索引闭区间 [left,right] 称为一个「窗口」。
- 我们先不断地增加 right 指针扩大窗口 [left,right] ,直到窗口中的字符串符合要求(包含了T中的所有字符串)。
- 此时,我们停止增加 right ,转而不停增加 left 指针缩小窗口 [left,right],直到窗口中的字符串不再符合要求(不包含T中的所有字符串了)。同时,每次增加left,我们都需要更新一轮新结果。
- 重复第2和第3步,直到 right 到达字符串S的尽头。
步骤2用于寻找一个「可行解」,然后步骤3用于优化这个「可行解」,最终找到最优解。
画解算法
伪代码
int left = 0, right = 0;while (right < s.size()) {// 增大窗口window.add(s[right]);right++;while (window needs shrink) {// 缩小窗口window.remove(s[left]);left++;}}
经典使用
题目:连续元素最大和
给定数组,获取数组中n个连续元素,最大的和

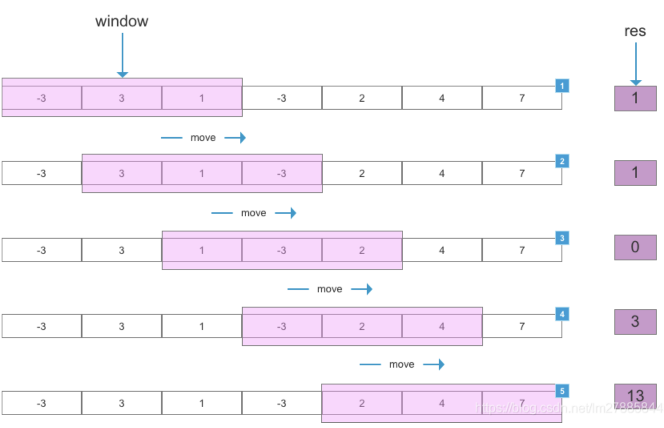
暴力算法 ```javascript function maxSumSub(arr, n) { let maxSum = 0;
if (n > arr.length) {
return arr;
}
for (let i = 0; i + n - 1 < arr.length; i++) {
let tempSum = arr[i]; for (let j = 1; j < n; j++) { tempSum += arr[i + j]; } maxSum = Math.max(maxSum, tempSum);} return maxSum; }
console.log(maxSumSub([-3, 3, 1, -3, 2, 4, 7], n = 3));
因为包含两个for循环,它的时间复杂度是O(k*n)。
- **滑动窗口算法**
```javascript
function maxSumSub(arr, n) {
let maxSum = 0;
if (n > arr.length) {
return arr;
}
// 定义窗口并确定值
for (let i = 0; i < n; i++) {
maxSum += arr[i];
}
let windowSum = maxSum;
// 窗口逻辑
for (let i = n; i < arr.length; i++) {
windowSum += arr[i] - arr[i - n];
maxSum = Math.max(maxSum, windowSum);
}
return maxSum
}
时间复杂度是O(n)。
题目:LC3.无重复字符串的最长子串
给定一个字符串,请找出其中不含有重复字符的 最长子串 的长度。
输入: s = “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
输入: s = “bbbbb”
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
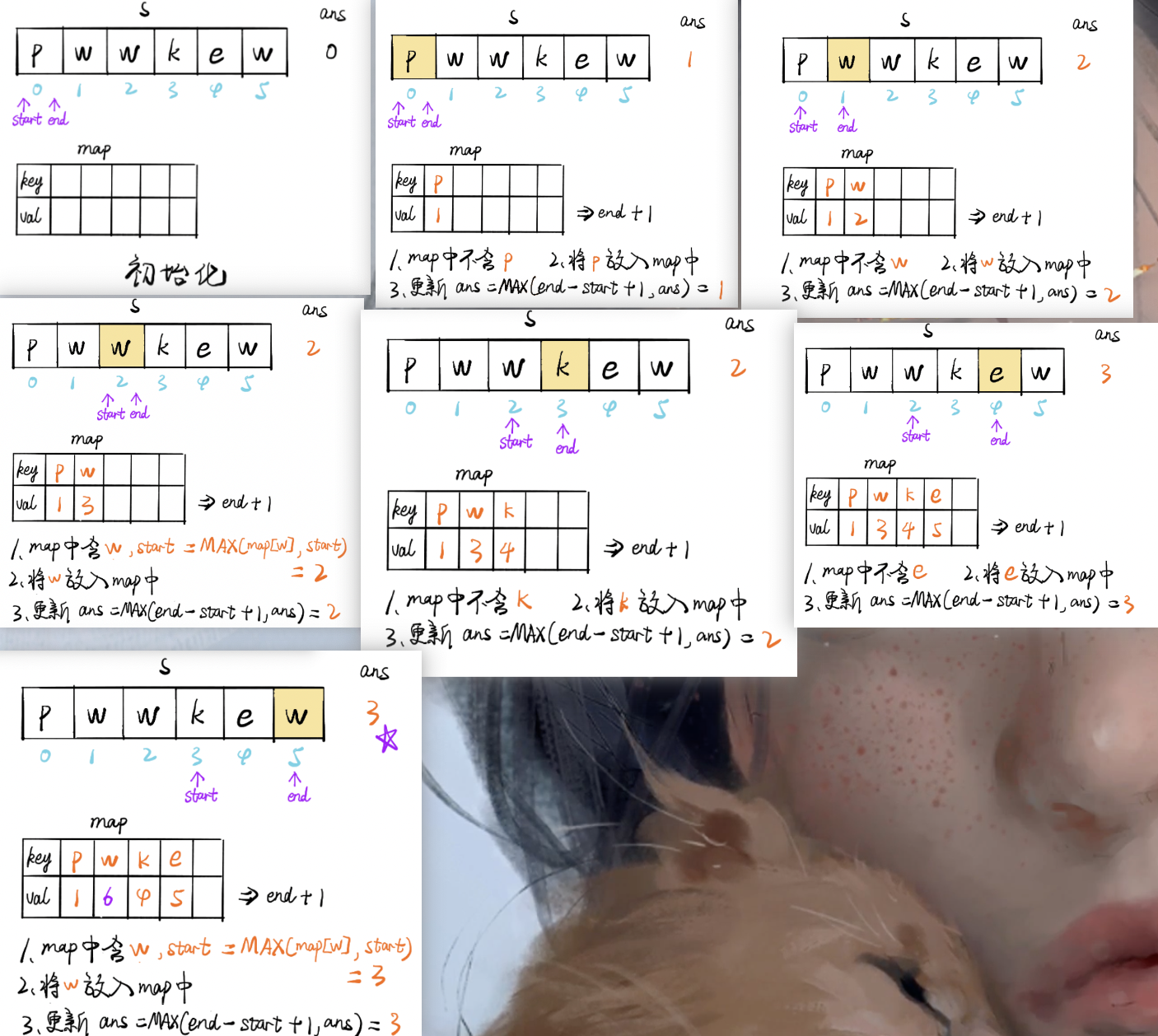
输入: s = “pwwkew”
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
输入: s = “”
输出: 0
- 暴力破解:
逐个生成子字符串,看它是否不含有重复的字符
两层for循环生成子串,第一层遍历子串的起始字符,第二层遍历子串的终止字符。对于每个子串再遍历判断是否不含有重复字符。
执行用时:258ms(13.83%)、内存消耗43.8MB(27%)
var lengthOfLongestSubstring = function (s) {
let maxLength = 0;
if (s.length === 1) return maxLength = 1;
for (let i = 0; i < s.length; i++) {
let curString = s.charAt(i);
for (let j = i + 1; j < s.length; j++) {
if (curString.indexOf(s.charAt(j)) === -1) {
curString += s.charAt(j);
} else {
maxLength = Math.max(curString.length, maxLength);
break;
}
}
maxLength = Math.max(curString.length, maxLength);
}
return maxLength;
};
- 模拟滑动窗口算法思路:
执行用时:128ms(43%)、内存消耗43.9MB(24%)
var lengthOfLongestSubstring = function (s) {
let maxLength = 0;
let curString = [];
for (let i = 0; i < s.length; i++) {
if (curString.indexOf(s.charAt(i)) === -1) {
curString.push(s.charAt(i));
} else {
maxLength = Math.max(maxLength, curString.length);
curString.push(s.charAt(i));
// 确定left指针;
curString = curString.slice(curString.indexOf(s.charAt(i)) + 1)
}
}
maxLength = Math.max(maxLength, curString.length);
return maxLength;
};
滑动窗口算法:
设置 left 作为左指针,指无重复字符串的首字符下标
设置 right 作为右指针用于记录无重复字符串的尾字符下标,因为当前无重复字符串可能不是最大字符串,所以需要用 ans 记录
遍历字符串,right 作为遍历索引
设置 Map 作为字符字典,存放遍历过程中的每个字符上次出现的索引,以当前字符作为 key,上次出现的下标作为 value。如果遇到重复字符则更新
用此种规则存放字符,如果出现重复字符则会更新,比如字符串 “abcba”,当 right === 3 时 map 中的 “key = b” 的值就会从 1 更新到 3
同时 map 中还会存放着垃圾数据,比如字符串 “abcba”,当 right === 3 时 map 中的 “key = b” 的值更新为了 3,此时说明窗口已经滑动到了 “c” 字符的位置,所以此时 map 中的 “key = a” 则为无效字符;当 right === 4 时当前字符为 “a” 此时查询 map 能查到对应的字符 “key = a” 但是因为它已经是无效字符,所以此时的“a”不是重复字符,因此需要 left 来控制窗口左边位置,当从 map 中查询到的字符时,此字符对应的索引 value 只有在 left 要求的范围内,才算重复字符
设置 Previous ( Map.get(key) )存放当前项在 map 中取出的值,即是当前字符上次出现的下标位置。
遍历过程中,如果 Previous存在 && curIndex>= left 代表当前字符已经出现过,并且在窗口内,则证明此时发生了重复,所以可以将左指针移向与当前位置重复的位置的下一个位置,比如字符串 “abcba”,当 i===3 时,与 i===1 的位置重复了,此时将左指针移动到 i===2 的位置
当前无重复字符串的长度等于当前索引 right + 1 - left,如果当前长度比历史的最大长度长,则更新历史的最大长度
执行用时:88ms(87.99%)、内存消耗40.1MB(83.37%)
var lengthOfLongestSubstring = function (s) {
if (!s || s.length < 1) return 0;
// 字符字典 存放当前字符上次出现的索引
let dic = new Map();
// 左右指针
let left = 0, right = 0;
// 答案answer
let ans = 0;
while (right < s.length) {
// 如果上次出现的索引比左指针大,则证明字符重复发生在窗口内,重复有效
if (dic.get(s[right]) >= left) {
// 将左指针移动到上此出现的索引的下一位,缩小当前窗口
left = dic.get(s[right]) + 1
}
// 将当前字符存放到 map 中,并记录最新索引
dic.set(s[right], right)
// 将当前统计的不重复字符串的长度与历史不重复字符串的长度对比,存储最大值
right++;
ans = Math.max(right - left, ans)
}
return ans
}
console.log(lengthOfLongestSubstring('pwwkew'))
题目:LC239.滑动窗口最大值
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回滑动窗口中的最大值。
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
————————— ——-
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
输入:nums = [1,-1], k = 1
输出:[1,-1]
输入:nums = [9,11], k = 2
输出:[11]

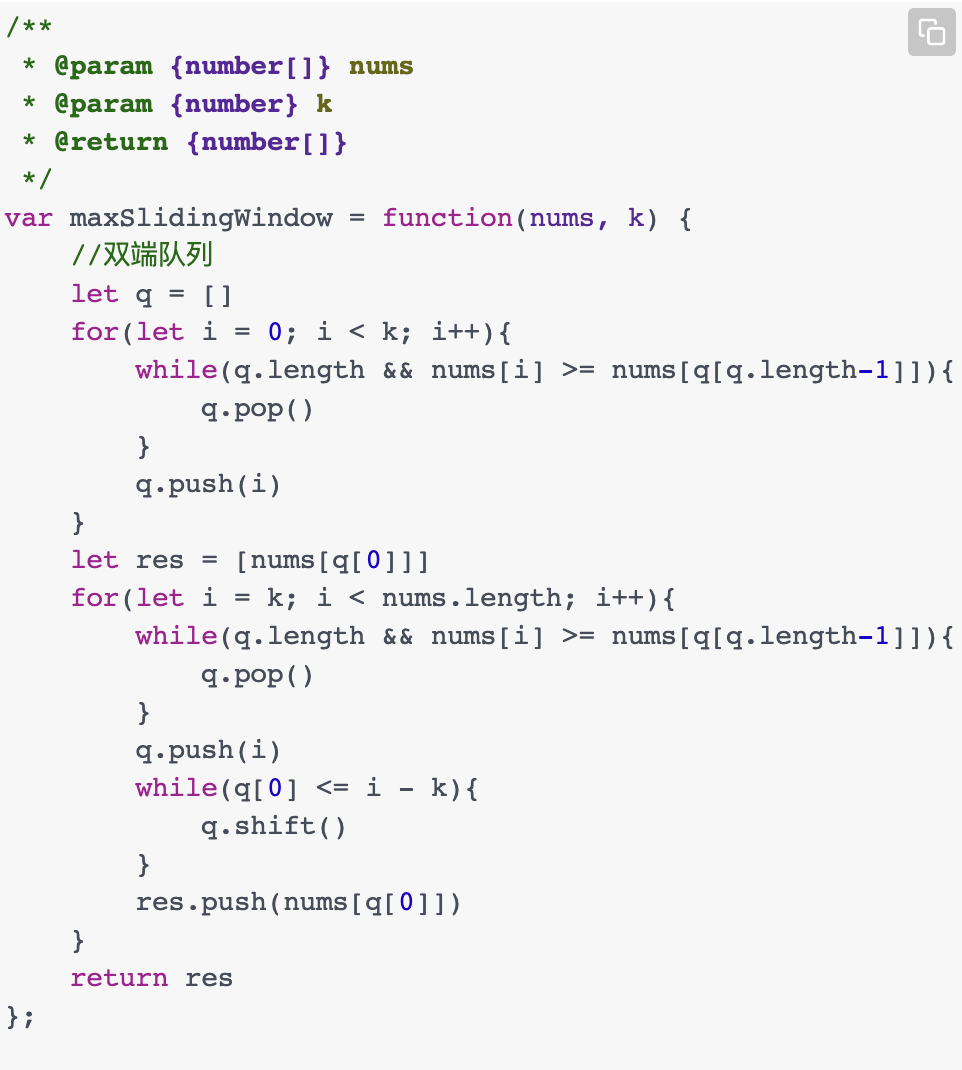
var maxSlidingWindow = function (nums, k) {
//单调队列数组,存放的是元素的下标,为了取值方便(存放窗口中值的下标)
const queue = [];
// 结果数组
const ans = [];
for (let i = 0; i < nums.length; i++) {
// 若队列有值 且 当前元素大于等于队尾所存下标的元素,则弹出队尾(当前元素>队尾元素,则弹出队列)
while (queue.length && nums[i] >= nums[queue[queue.length - 1]]) {
queue.pop();
}
// 入队 当前元素的下标
queue.push(i)
// 判断当前最大值(即队首元素)是否在窗口中,若不在便将其出队(队首值的下标大于i-k)
while (queue[0] <= i - k) {
queue.shift();
}
// 当达到窗口大小时便开始向结果中添加元素
if (i >= k - 1) ans.push(nums[queue[0]]);
}
return ans
};
console.log(maxSlidingWindow([1, 3, -1, -3, 5, 3, 6, 7], k = 3))
由于我们需要求出的是滑动窗口的最大值,如果当前的滑动窗口中有两个下标 ii 和 jj,其中 ii 在 jj 的左侧(i < ji<j),并且 ii 对应的元素不大于 jj 对应的元素(\textit{nums}[i] \leq \textit{nums}[j]nums[i]≤nums[j]),那么会发生什么呢?
当滑动窗口向右移动时,只要 ii 还在窗口中,那么 jj 一定也还在窗口中,这是 ii 在 jj 的左侧所保证的。因此,由于 \textit{nums}[j]nums[j] 的存在,\textit{nums}[i]nums[i] 一定不会是滑动窗口中的最大值了,我们可以将 \textit{nums}[i]nums[i] 永久地移除。
因此我们可以使用一个队列存储所有还没有被移除的下标。在队列中,这些下标按照从小到大的顺序被存储,并且它们在数组 \textit{nums}nums 中对应的值是严格单调递减的。因为如果队列中有两个相邻的下标,它们对应的值相等或者递增,那么令前者为 ii,后者为 jj,就对应了上面所说的情况,即 \textit{nums}[i]nums[i] 会被移除,这就产生了矛盾。
当滑动窗口向右移动时,我们需要把一个新的元素放入队列中。为了保持队列的性质,我们会不断地将新的元素与队尾的元素相比较,如果前者大于等于后者,那么队尾的元素就可以被永久地移除,我们将其弹出队列。我们需要不断地进行此项操作,直到队列为空或者新的元素小于队尾的元素。
由于队列中下标对应的元素是严格单调递减的,因此此时队首下标对应的元素就是滑动窗口中的最大值。但与方法一中相同的是,此时的最大值可能在滑动窗口左边界的左侧,并且随着窗口向右移动,它永远不可能出现在滑动窗口中了。因此我们还需要不断从队首弹出元素,直到队首元素在窗口中为止。
为了可以同时弹出队首和队尾的元素,我们需要使用双端队列。满足这种单调性的双端队列一般称作「单调队列」。

