概念

链表实际上是线性表的链式存储结构，与数组不同的是，它是用一组任意的存储单元来存储线性表中的数据，存储单元不一定是连续的，
且链表的长度不是固定的，链表数据的这一特点使其可以非常的方便地实现节点的插入和删除操作。

链表是有序的数据结构
可以从首、尾、中间进行数据存取。
Q：为什么不使用数组
A：数组在内存中占用一段连续的空间，添加、移除会导致后续元素位移，性能开销大。

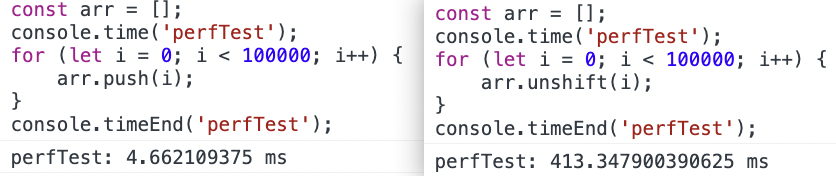
总结：

链表是有序的数据结构，链表中的每个部分称为节点。
链表可以从首、尾、中级进行数据存取。
链表的元素在内存中不必是连续的空间。
优点：添加与删除不会导致其余元素位移。
缺点：无法根据索引快速定位元素。
链表的实现

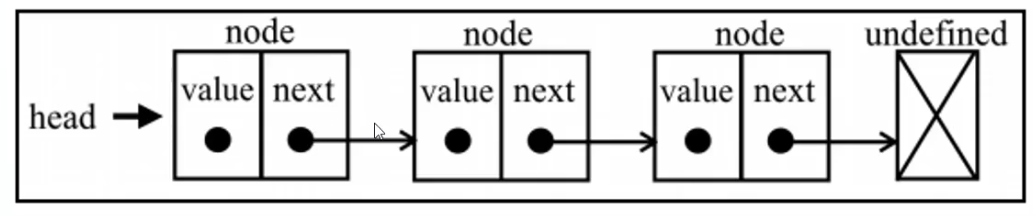
我们需要实现以下功能：

节点类：
- value 存储当前节点数据
- next 存储下一个节点的指针
链表类：
- addAtTail(value) 尾部添加节点
- addAtHead(value) 头部添加节点
- addAtIndex(value, index) 指定位置添加节点
- get(index) 获取节点
- removeAtIndex(index) 删除指定节点

// 节点类
class LinkedNode {
    constructor(value) {
        // 存储当前节点数据
        this.value = value;
        // 用于存储下一个节点的引用
        this.next = null;
    }
}
// 链表类
class LinkedList {
    constructor() {
        this.count = 0;
        this.head = null;
    }
    // 添加节点(尾)
    addAttail(value) {
        // 创建新节点
        const node = new LinkedNode(value);
        // 检测链表是否存在数据
        if (this.count === 0) {
            this.head = node;
        } else {
            // 找到链表尾部节点，将尾部节点的 next 设置为 node
            // Q：如何找到尾部节点呢？
            // A：链表不同数组可以通过 length-1 找到尾部节点，所以我们需要使用 head 一直访问 next 直到没有next为止。
            let cur = this.head;
            while (cur.next !== null) {
                cur = cur.next;
            }
            cur.next = node;
        }
        this.count++;
    }
    // 添加节点(头)
    addAtHead(value) {
        const node = new LinkedNode(value);
        if (this.count === 0) {
            this.head = node;
        } else {
            // 将 node 添加到 head 的前面
            node.next = this.head;
            this.head = node;
        }
        this.count++;
    }
    // 获取节点(根据索引，类似数组，索引0指向head)
    get(index) {
        // 合法检测
        if (this.count === 0 || index < 0 || index >= this.count) {
            console.log('不合法，获取节点失败');
            return;
        }
        // 迭代链表，找到对应节点
        let current = this.head;
        for (let i = 0; i < index; i++) {
            current = current.next;
        }
        return current;
    }
    // 添加节点(根据索引)
    addAtIndex(value, index) {
        // 合法检测
        if (this.count === 0 || index >= this.count) {
            console.log('不合法，添加节点失败');
            return;
        }
        // 如果 index <= 0，默认添加到头部即可。
        if (index <= 0) {
            return this.addAtHead(value);
        }
        // 后面为正常区间处理，将 node 添加到 get(index) 前面
        const prev = this.get(index - 1);
        const node = new LinkedNode(value);
        node.next = prev.next;
        prev.next = node;
        this.count++;
    }
    // 删除节点(根据索引)
    removeAtIndex(index) {
        // 合法检测
        if (this.count === 0 || index < 0 || index >= this.count) {
            console.log('不合法，删除节点失败');
            return;
        }
        if (index === 0) {
            this.head = this.head.next;
        } else {
            const prev = this.get(index - 1);
            prev.next = prev.next.next;
        }
        this.count--;
    }
}
const l = new LinkedList();

链表的多种形式

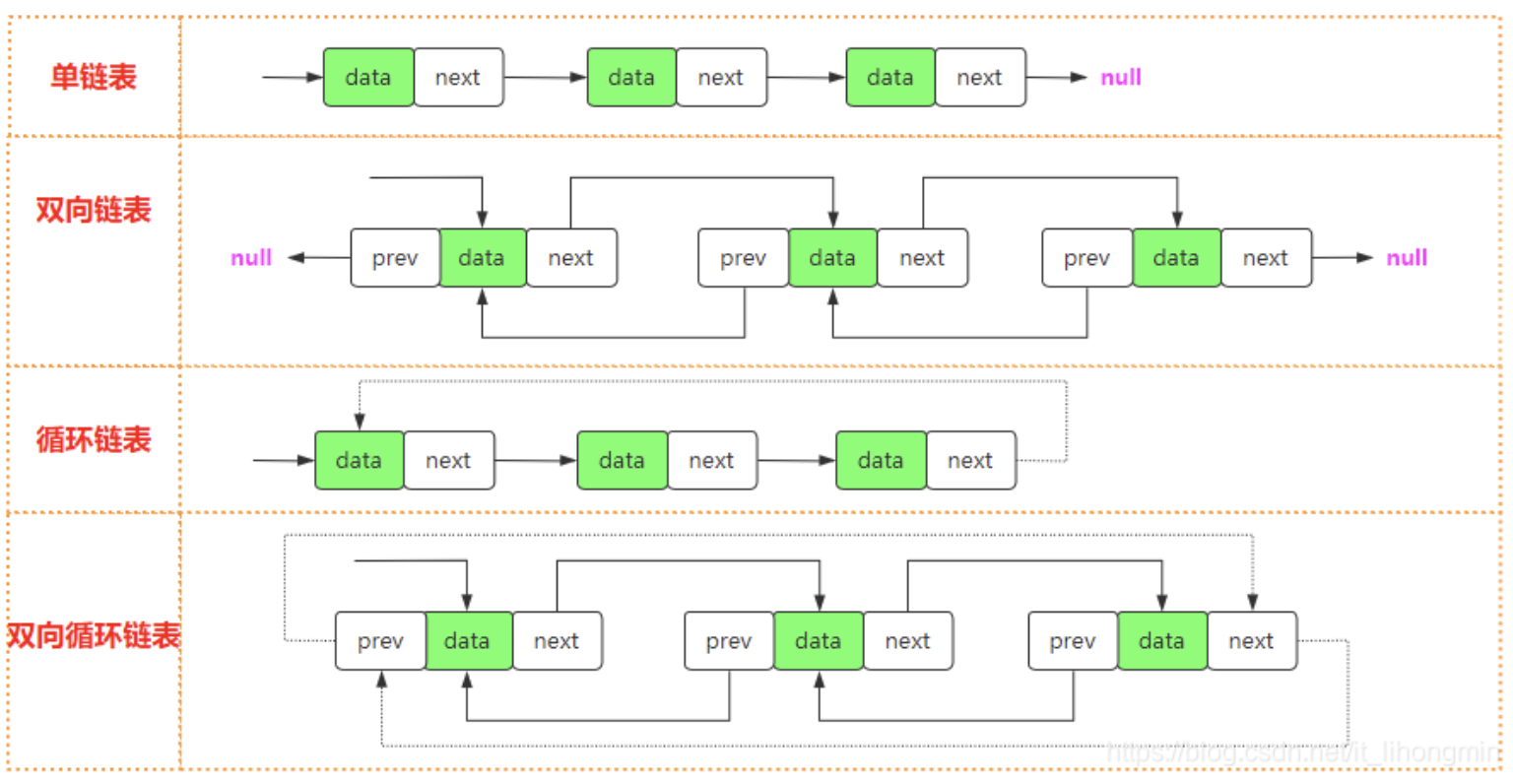
双向链表（双端链表）

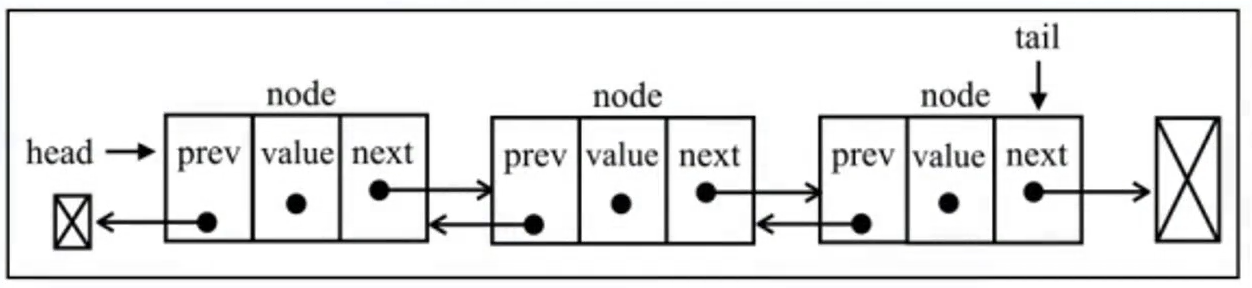
双向链表指的是在普通链表的基础上，增加一个用于记录上一个节点的属性 prev ，可以进行双向访问。

循环链表（环形链表）

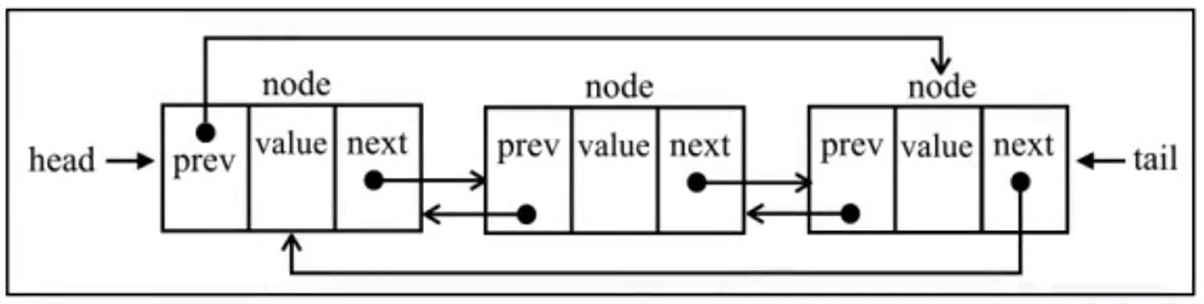
循环链表指的是链表最后一个节点的 next 指向第一个节点 head ，形成首尾相连的循环结构。
在实际使用中，环的结束点可以为链表的任意节点。（尾部节点next 指向任意节点都可以成为循环链表）

力扣精选题

leetcode 206.反转链表

206. 反转链表(简单)

方法一：迭代反转链表

思路：迭代链表，将当前项的 next = next的前一项

var reverseList = function (head) {
    // 声明变量记录 prev、curr
    let prev = null;
    let curr = head;
    // 当 curr 是节点时，进行迭代
    while (curr !== null) {
        // 先保存当前节点的下一个节点
        const next = curr.next;
        curr.next = prev;
        prev = curr;
        curr = next;
    }
    return prev;
};

时间复杂度：O(n)，n 为链表的长度。需要遍历一次链表。
空间复杂度：O(1)，只需要常数的空间存放若干变量。

方法二：递归反转链表（尚未理解）

思路：用递归函数不断传入 head.next ，直到 head === null 或者 head.next === null ，到了递归的最后一层的时候，让后面一个节点指向前一个节点，然后让前一个节点的 next 置为空，直到到达第一层，就是链表的第一个节点，每一层都返回最后一个节点。

var reverseList = function (head) {
    if (head === null || head.next === null) {
        return head;
    }
    const newHead = reverseList(head.next);
    // 此时的 head 为4 最后一个节点指向前一个节点。
    head.next.next = head;
    head.next = null; // 前一个节点的 next 置为空。
    return newHead;
};

时间复杂度：O(n)，n 为链表的长度。需要对链表的每一个节点进行反转操作。
空间复杂度：O(n)，n 为链表的长度。递归的深度为 n。

面试题 02.08. 环路检测

LeetCode 面试题 02.08. 环路检测(中等)

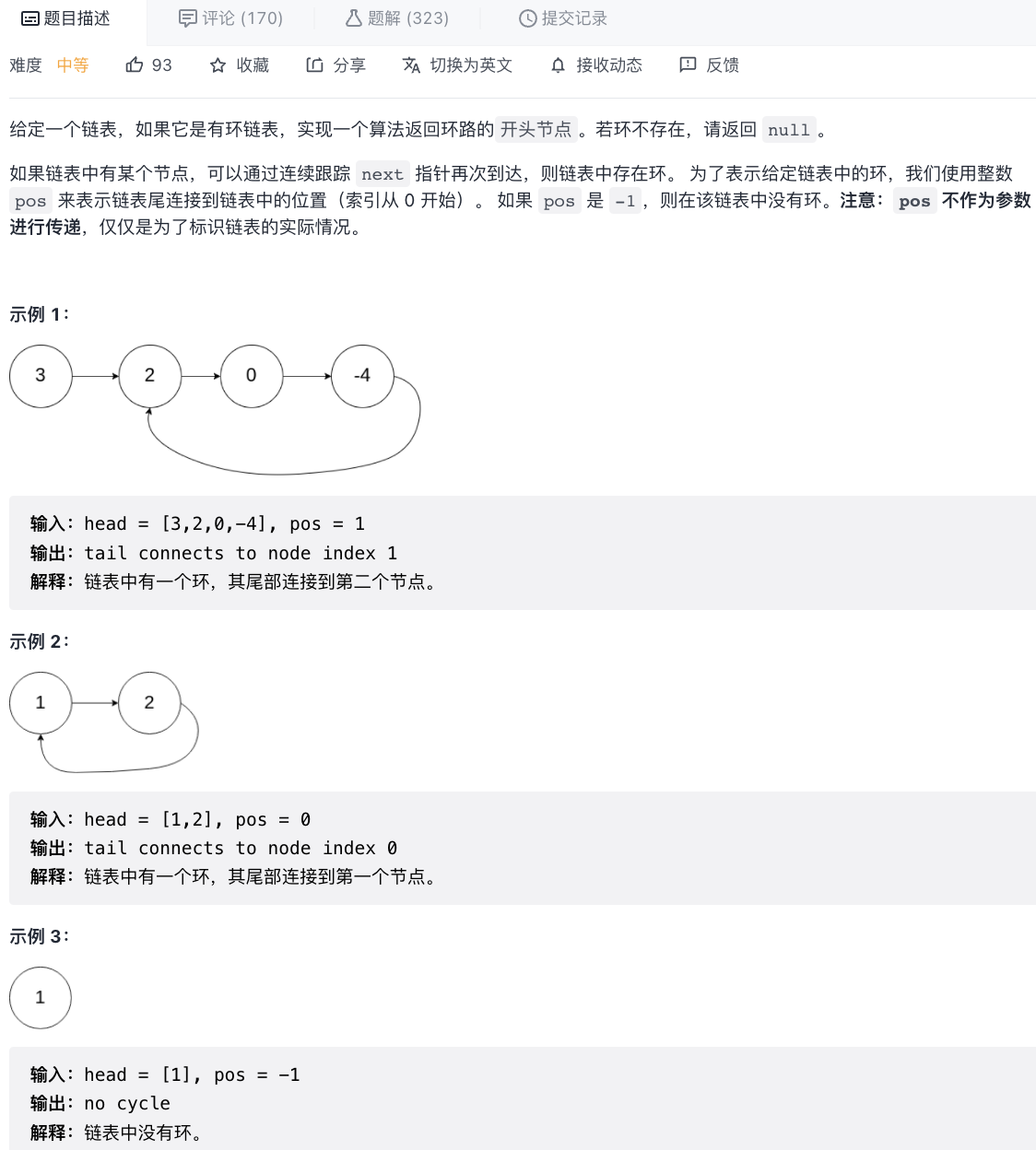
方法一：集合

思路：迭代遍历链表的每一个节点，并且将其记录与集合中，如果某个节点在集合中出现过，就可以判定链表中存在环。

var detectCycle = function (head) {
    const visited = new Set();
    while (head !== null) {
        // 判断集合中是否存在当前节点
        if (visited.has(head)) {
            return head;
        }
        // 不存在，则添加到集合中
        visited.add(head);
        head = head.next;
    }
    return head;
};

时间复杂度：O(n)，n 为链表的节点数目。我们需要访问链表的每一个节点。
空间复杂度：O(n)，n 为链表的节点数目。我们需要将链表中的每一个节点都保存到集合中。

方法二：快慢指针

步骤一：判断是否为有环链表定义两个指针 fast slow。fast 每次移动 2 位，slow 每次移动 1 位。如果相遇，则说明链表中存在环。

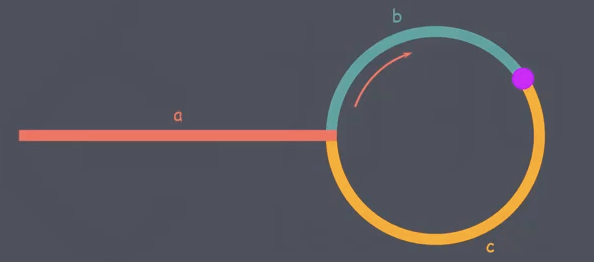
步骤二：找到入环点如下图所示，设链表中环外部分的长度为 a。slow 指针进入环后，又走了 b 的距离与 fast 相遇。此时，fast 指针已经走完了环的 n 圈。 fast 移动距离为：a+n(b+c)+b slow 移动距离为：a+b 又因：速度比为 2:1 即在任意时刻 fast 指针走过的距离都为 slow 的 2倍得：a+n(b+c)+b = 2(a+b) 交互处理的：a = (n-1)(b+c)+c 根据这层等量关系，我们可得：从相遇点到入环点的距离(图中c的长度)，恰好等于从链表头部到入环点的距离。此时再定一个一个新指针 ptr 因此，当 slow 和 fast 相遇时，我们再额外定义一个 ptr 指针。起始阶段指向链表头部，然后 prt 和 slow 每次向后移动一个位置。最终会在入环点相遇。

var detectCycle = function (head) {
    // 特殊情况处理 
    if (head === null || head.next === null) {
        return null;
    }
    // 使用快慢指针判断是否存在环
    let fast = head, slow = head;
    while (fast !== null) {
        slow = slow.next;
        // fast 为尾部节点，则不存在环 返回null，否则移动两位
        if (fast.next === null) {
            return null;
        }
        fast = fast.next.next;
        // 判断是否快慢指针是否相遇，相遇则存在环
        if (slow === fast) {
            // 找到入环点
            let prt = head;
            while (prt !== slow) {
                prt = prt.next;
                slow = slow.next;
            }
            // slow 和 prt 的交点即是入环点
            return prt;
        }
    }
    // while循环结束，说明 fast 为 null，即不存在环，返回null
    return null;
};

时间复杂度：O(n)，n 为链表的节点数目。

第一步判断是否存在节点，slow 指针走过的距离不会超过链表的总长度；
第二步寻找入环点，走过的距离也不会超过链表的总长度。

空间复杂度：O(1)，只需要常数的空间存放若干变量，即 slow fast prt 三个指针。

链表