树的概念
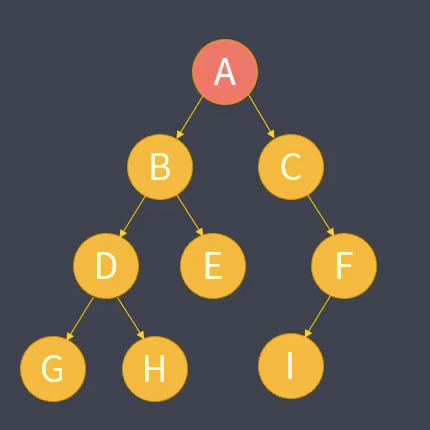
数形结构是一种非线性数据结构。
树中的每个部分称为结点,结点间存在分支结构与层次关系。
结点:
- 每个树形结构都存在一个根结点(A)。
- 根据结点之间的关系,存在 父结点、子结点、兄弟结点 的概念。
- 不含子结点的结点称为叶结点(G、H、I)。
子树:
- 对某个结点与其后代结点的整体称呼。
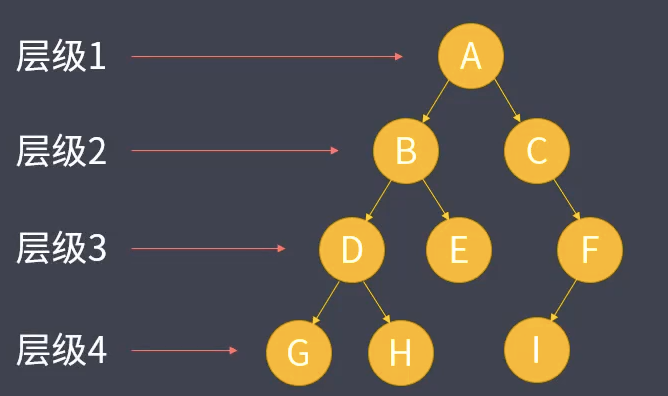
由于存在父子关系,树中的结点形成多级结构,称为层级。
- 根结点层级为 1 ,向下依次递增。
- 树中最深结点的层级称为树的高度(层级4)。
二叉树
二叉树是树形结构中的一种,二叉树中的每个结点最多只能存在2个子结点,因此有 左子结点、右子结点、左子树、右子树。
满二叉树
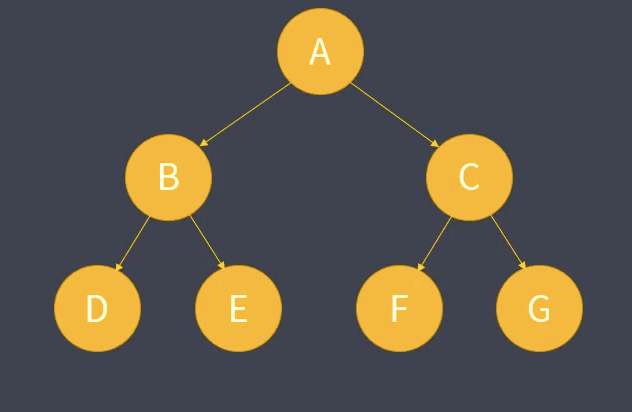
如上图,二叉树的每一层结点都达到最大值,称为满二叉树。
完全二叉树
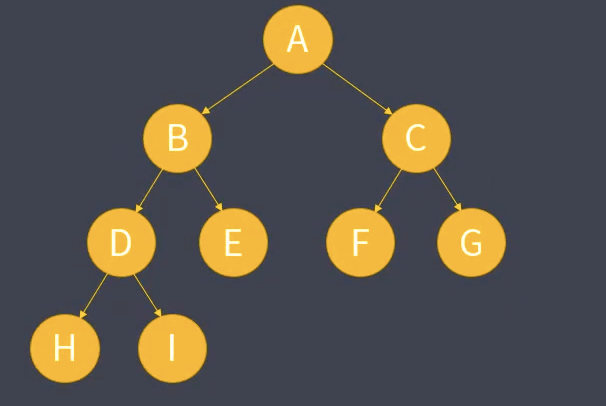
二叉树除最后一层外,每层结点都达到最大值,且最后一层结点都位于左侧,这种形式称为完全二叉树。
满二叉树也属于完全二叉树。
Q:为什么二叉树会有这么多分类?
A:对于不同的二叉树形式,我们可以使用不同的存储方式进行存储。
二叉搜索树
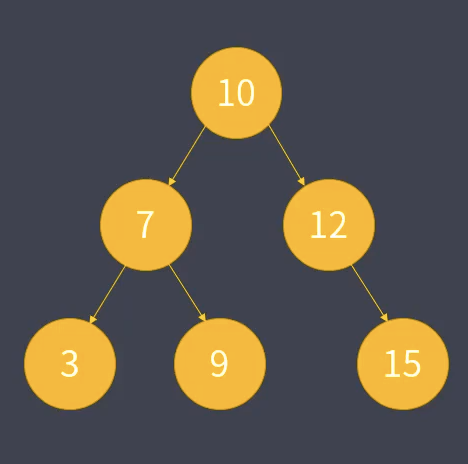
二叉搜索树是一种特殊的二叉树,简称BST(Binary Search Tree)
目的:是为了提高查找的性能,其查找在平均和最坏的情况下都是logn级别,接近二分查找。
其特点是:左子树的结点小于根结点,右子树的结点大于根结点。 
二叉查找树还有一个性质,即对二叉查找树进行中序遍历,即可得到有序的数列。
二叉树的存储形式
顺序存储(数组)
由于完全二叉树的结构连续,有迹可循,可采用顺序存储方式。
如按照从左往右,从上到下的顺序将结点存储在数组中。
非完全二叉树也可以采用顺序存储方式,遇到空结点用 null 占位即可,但是对空间有所浪费,得不偿失。
链式存储(链表)
普通二叉树由于结构不规则,不适合使用顺序存储,为了记录结点之间的关系,可使用链式存储方式。
每个结点通过 value 表示值,left、right 表示左右子结点。
二叉树的遍历方式
二叉树的遍历从根结点开始,根据数据访问的顺序不同存在三种遍历形式:前序遍历、中序遍历、后序遍历。
这里的序表示树根结点的访问顺序。
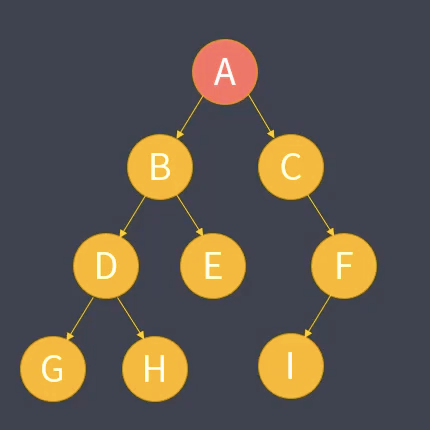
以该二叉树讲解遍历顺序。
前序遍历
按 根结点 -> 左子树 -> 右子树 顺序进行遍历。
上述二叉树前序遍历结果为:A BDGH E CFI
中序遍历
按 左子树 -> 根结点 -> 右子树 顺序进行遍历。
上述二叉树中序遍历结果为:GDH BE ACIF
后序遍历
按 左子树 -> 右子树 -> 根结点 顺序进行遍历。
上述二叉树后序遍历结果为:GHD EB IFC A
👍👍👍 史上最全遍历二叉树详解:
转自:LeetCode解题,Go语言全干工程师
力扣精选题
📖目录
🧭二叉树相关例题刷题指北
以下题目的题解和思路位于GitHub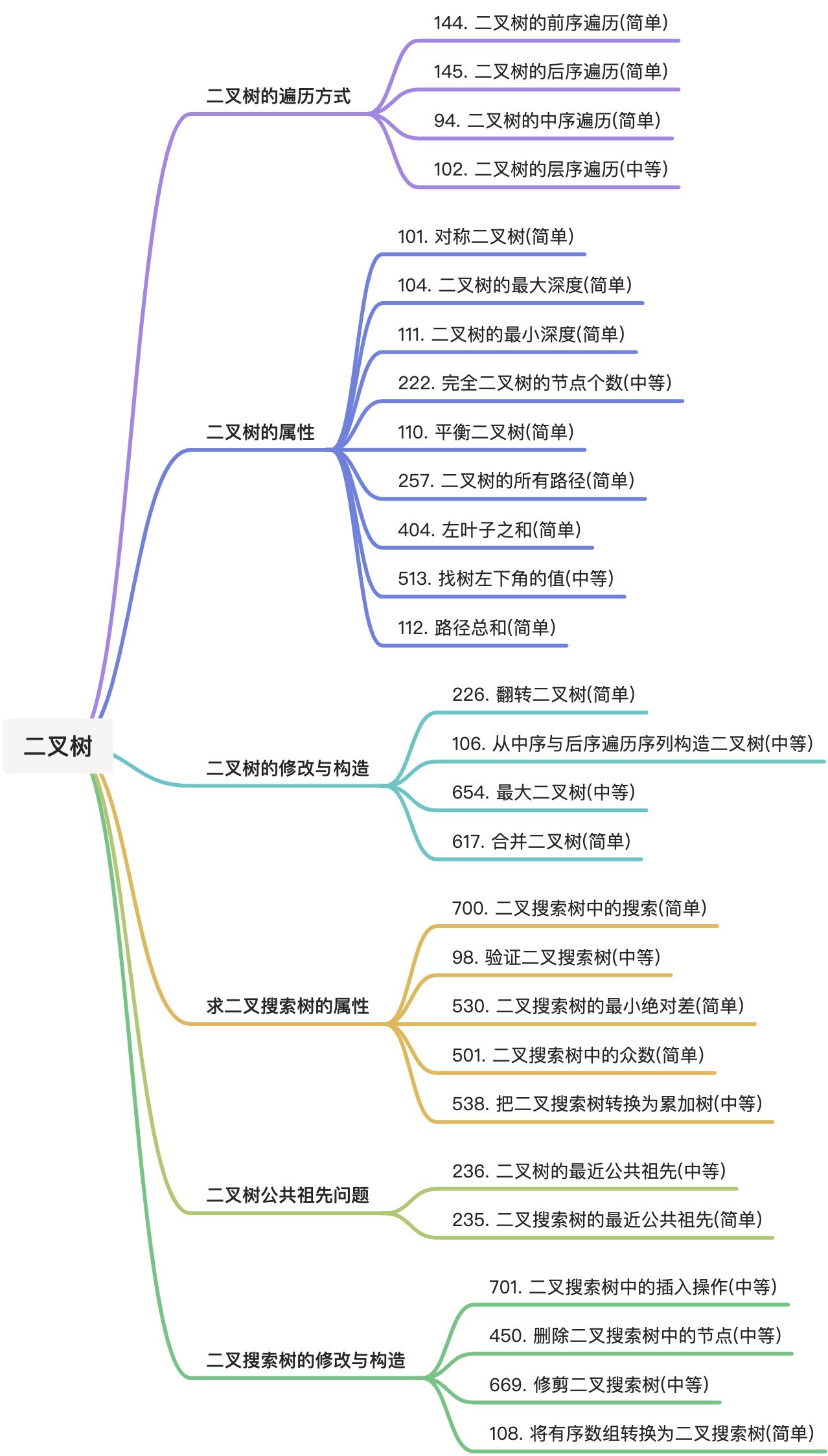
144. 二叉树的前序遍历
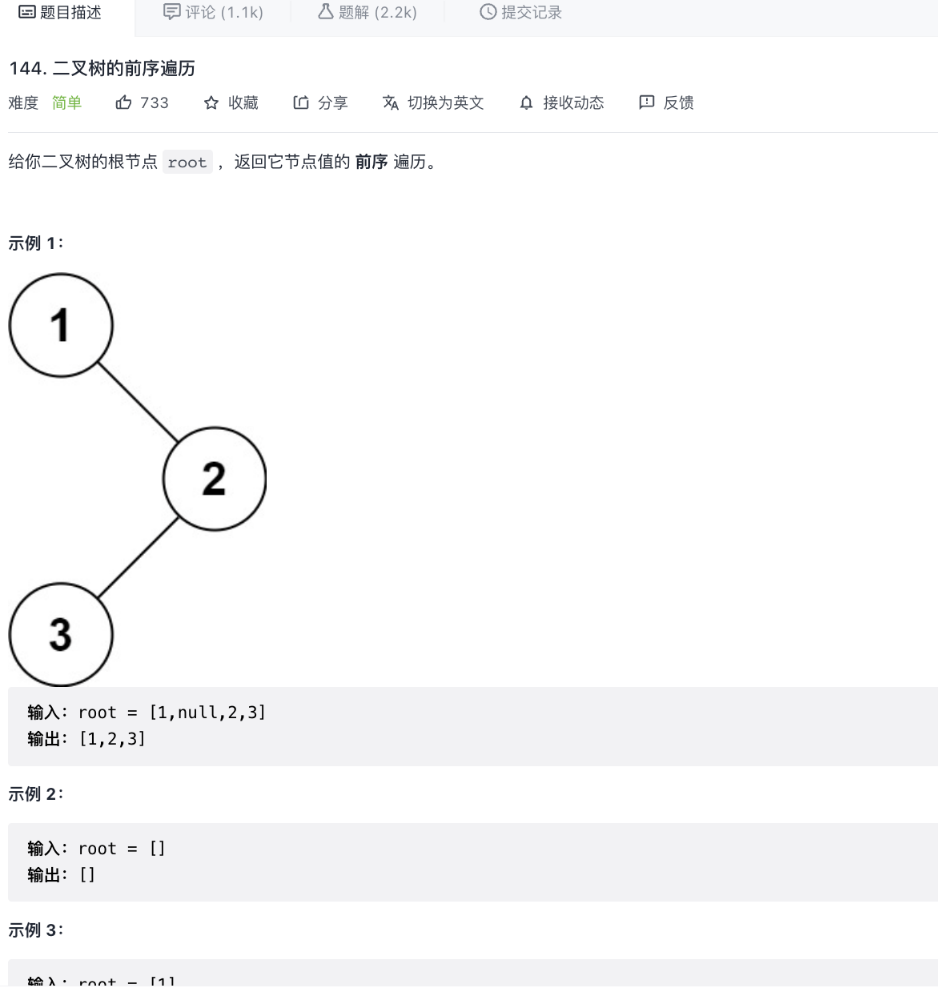
方法一:递归
var preorderTraversal = function (root) {
// 用于存储遍历的结果
const res = [];
const preorder = function (root) { // 参数root 为每个子树的根结点
if (root === null) return; // 设置递归出口
res.push(root.val); // 记录遍历到的根节点值
preorder(root.left); // 前序遍历左子树
preorder(root.right); // 前序遍历右子树
};
preorder(root);
return res;
};
时间复杂度:O(n),其中 n 为二叉树的节点,每一个节点只被遍历一次。
空间复杂度:O(n),为递归过程中栈的开销,平均情况为O(logn),最坏情况为树呈现链状,为O(n)。
方法二:迭代
额外声明一个栈,迭代二叉树。 先遍历左子树,记录节点,并将之后要遍历的右子树存入栈中。 左子树遍历完,查看栈是否有值,有值则表示还有未遍历的右子树,栈顶的右子树出栈作为根节点继续迭代。 直到栈为空,结束循环。
// 写法一:
var preorderTraversal = function (root) {
// 用于存储遍历的结果
const res = [];
// 用于存储未遍历的右子树
const stack = [];
// 迭代二叉树 根节点不为null 或 栈中有值
while (root !== null || stack.length) {
// 遍历左子树
while (root !== null) {
res.push(root.val); // 记录根节点
stack.push(root.right); // 未遍历的右子树入栈
root = root.left; // 迭代
}
// 迭代 遍历右子树
root = stack.pop();
}
return res;
};
// 写法二:每一个结点都入栈。
// 右结点后遍历所以先入栈,然后左结点入栈。一次性出栈。
var preorderTraversal = function (root) {
if (root === null) return [];
// 用于存储遍历的结果
const res = [];
// 用于存储未遍历的右子树
const stack = [root];
// 迭代二叉树 栈中有值
while (stack.length !== 0) {
root = stack.pop();
res.push(root.val); // 记录根节点
if (root.right !== null) stack.push(root.right);
if (root.left !== null) stack.push(root.left);
}
return res;
};
时间复杂度:O(n),n 为二叉树的节点,每一个节点只被遍历一次。
空间复杂度:O(n),为迭代过程中显示栈的开销,平均情况为O(logn),最坏情况为树呈链状,为O(n)。
104. 二叉树的最大深度(深度优先DFS)
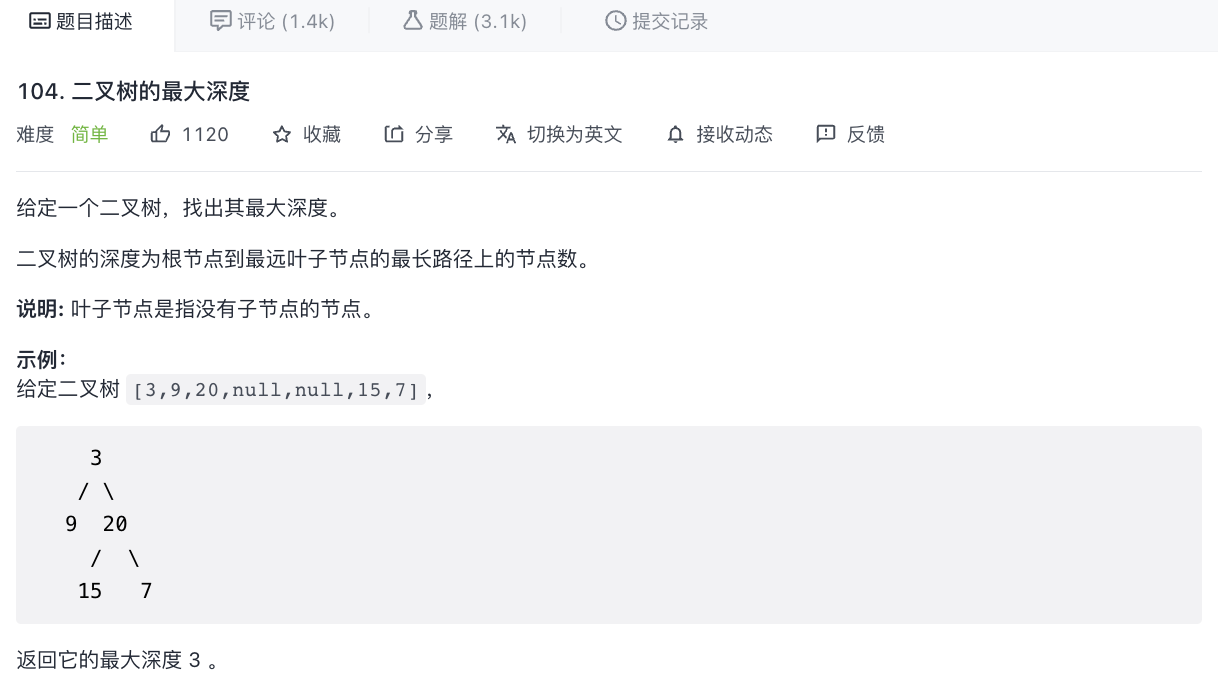
var maxDepth = function (root) {
if (root === null) return 0; // 递归设置出口
return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
};
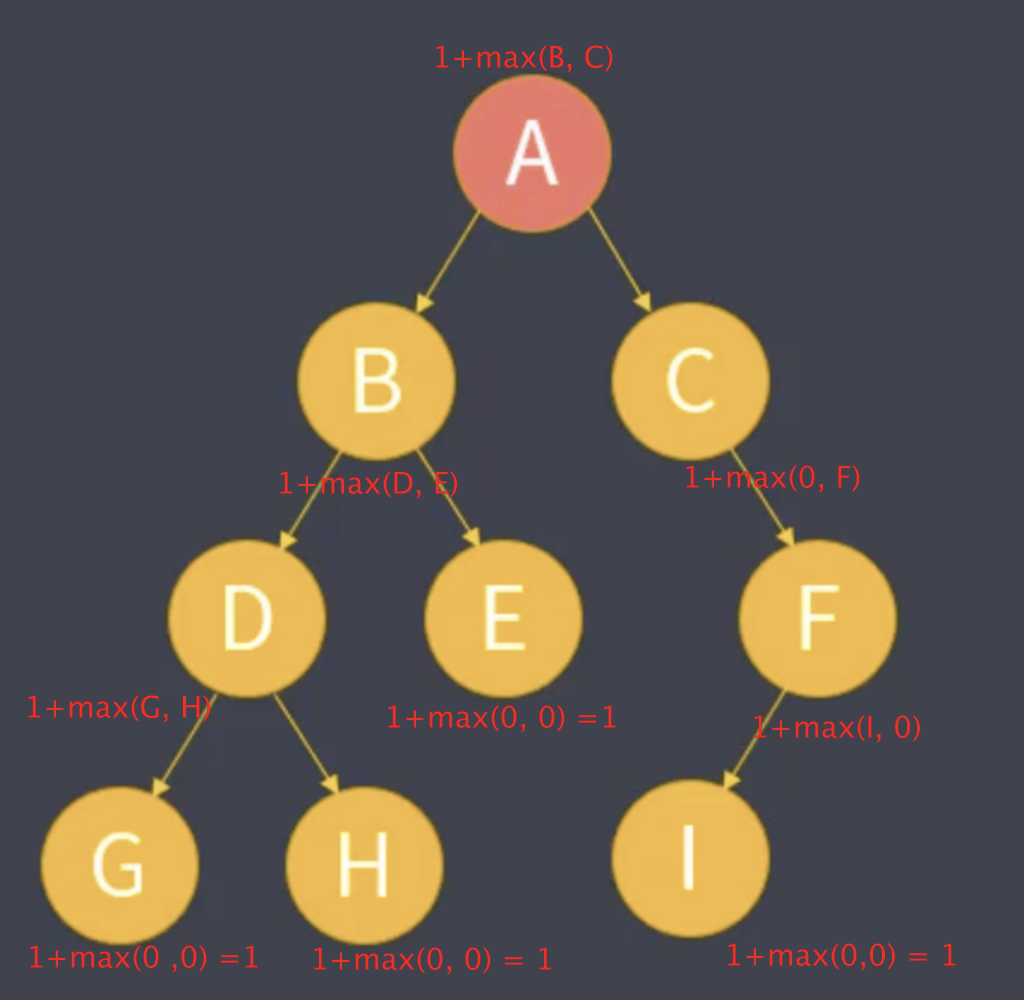
时间复杂度:O(n),n 为二叉树的结点数目,每一个节点只被遍历一次。
空间复杂度:O(n),n 为二叉树的深度,递归函数需要栈空间,栈空间取决于递归的深度。
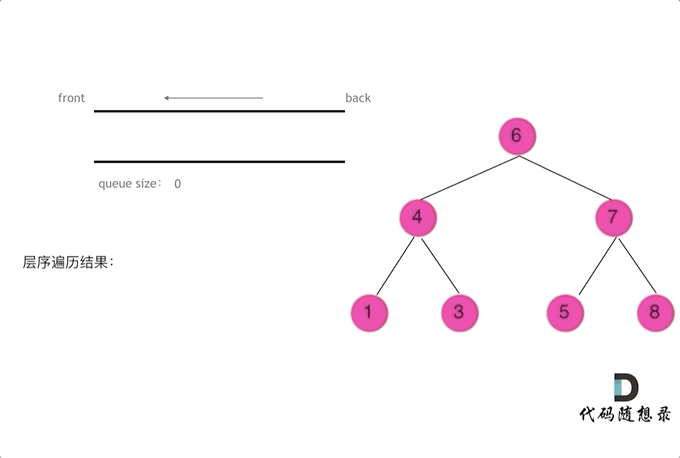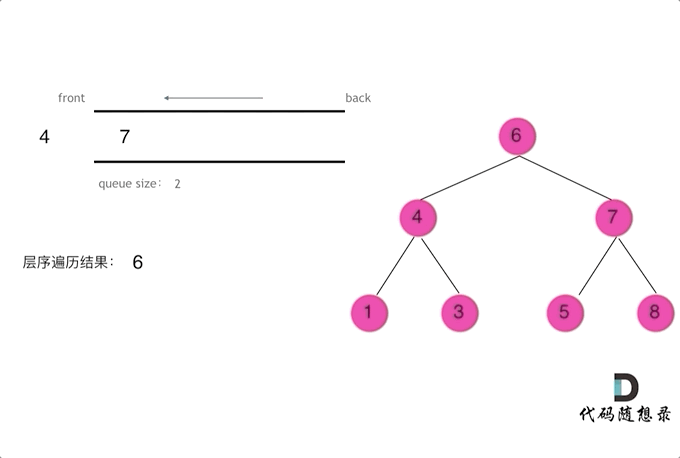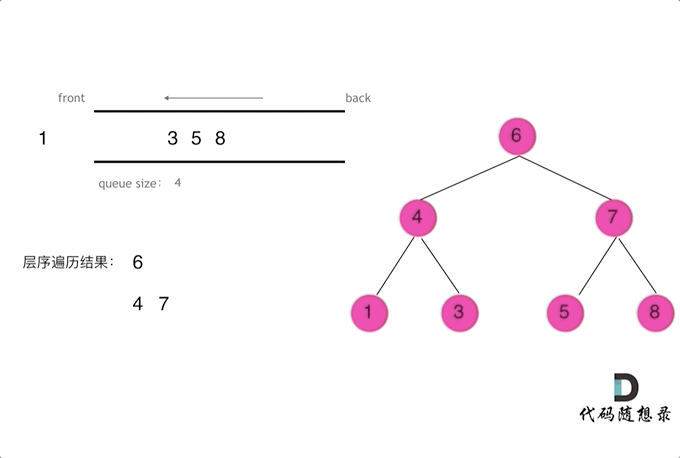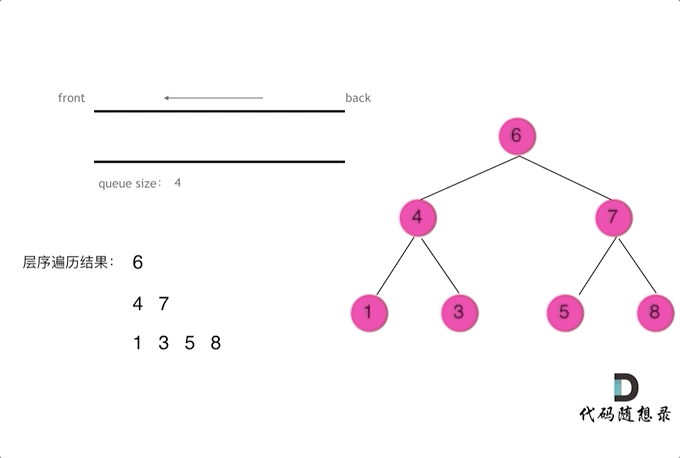
102. 二叉树的层序遍历(广度优先遍历BFS)
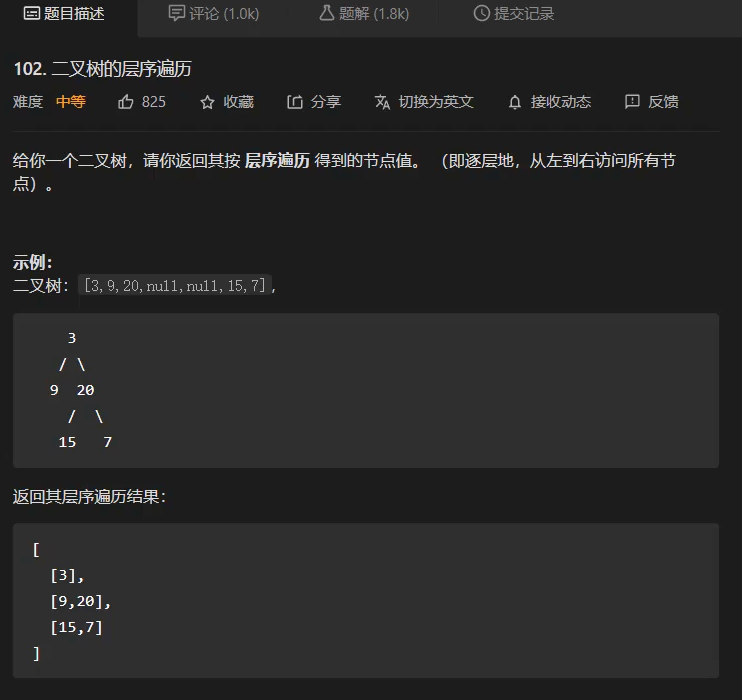
- 普通BFS遍历的结果:一维数组 [1, 2, 3, 4, 5, 6, 7, 8, 9]
无法区分队列中的结点来自那一层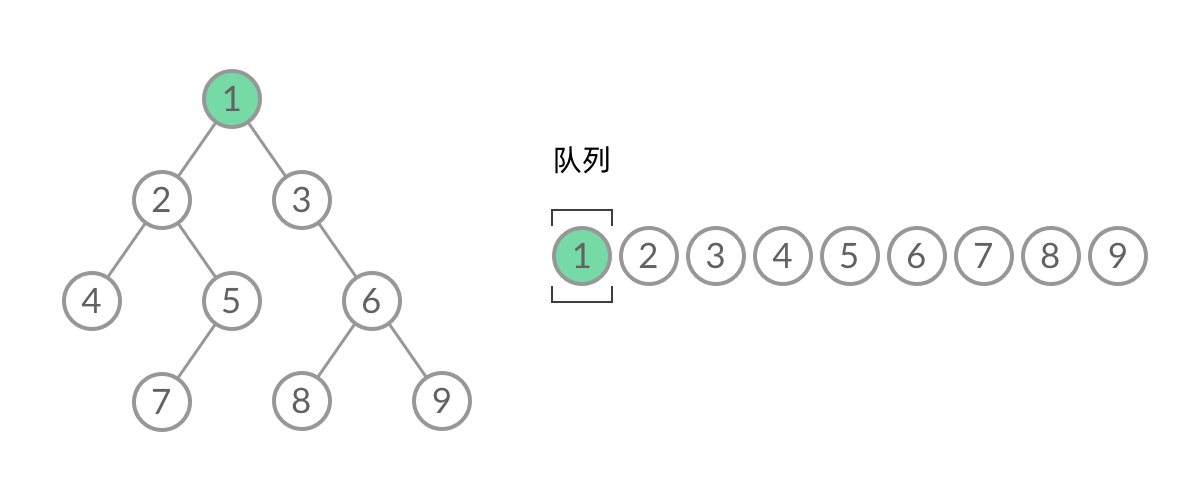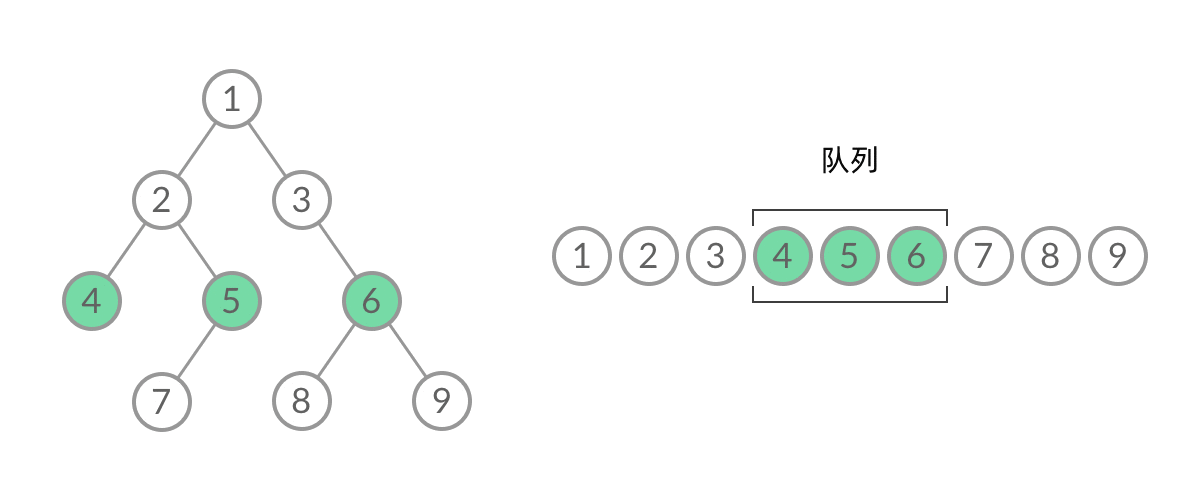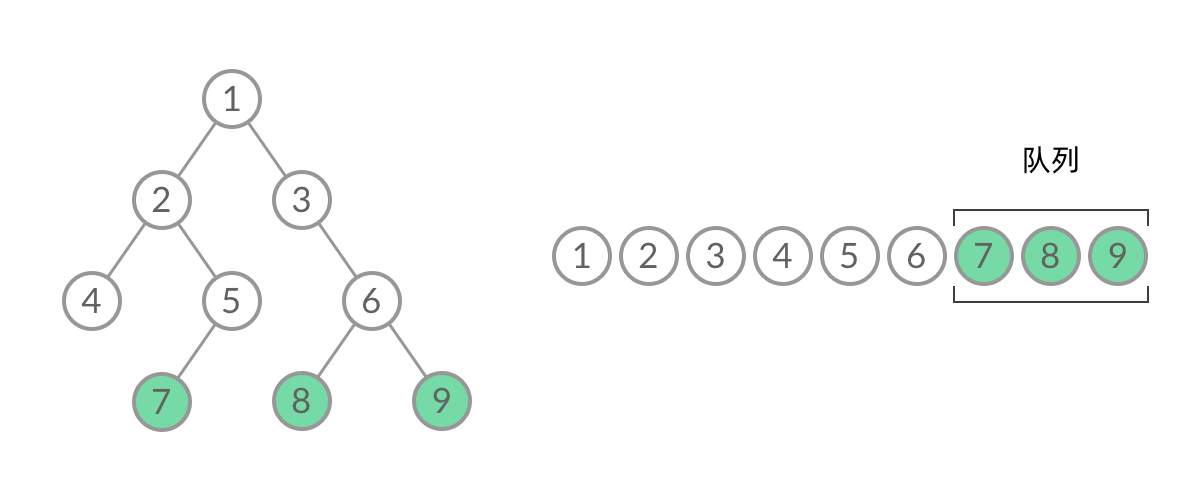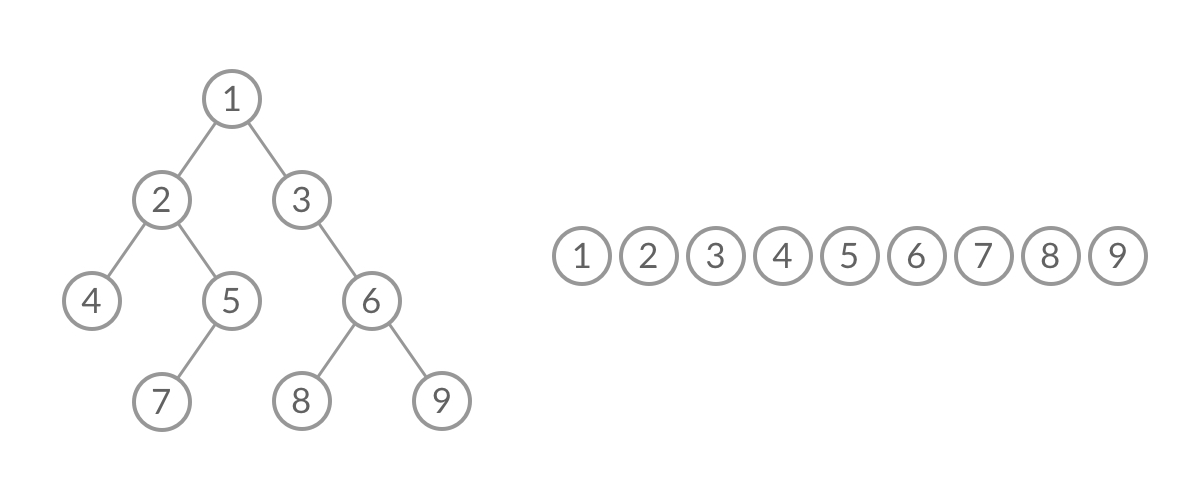
- 将BFS遍历改造成层序遍历:
在每一层遍历开始前,先记录队列中的结点数量 n(也就是这一层的结点数),然后一口气处理完这层的 n 个几点。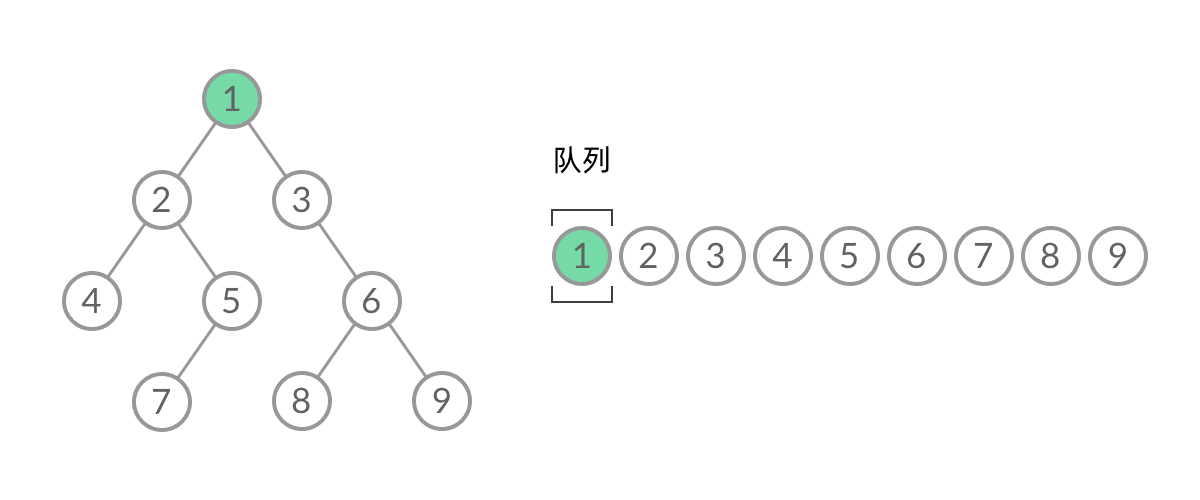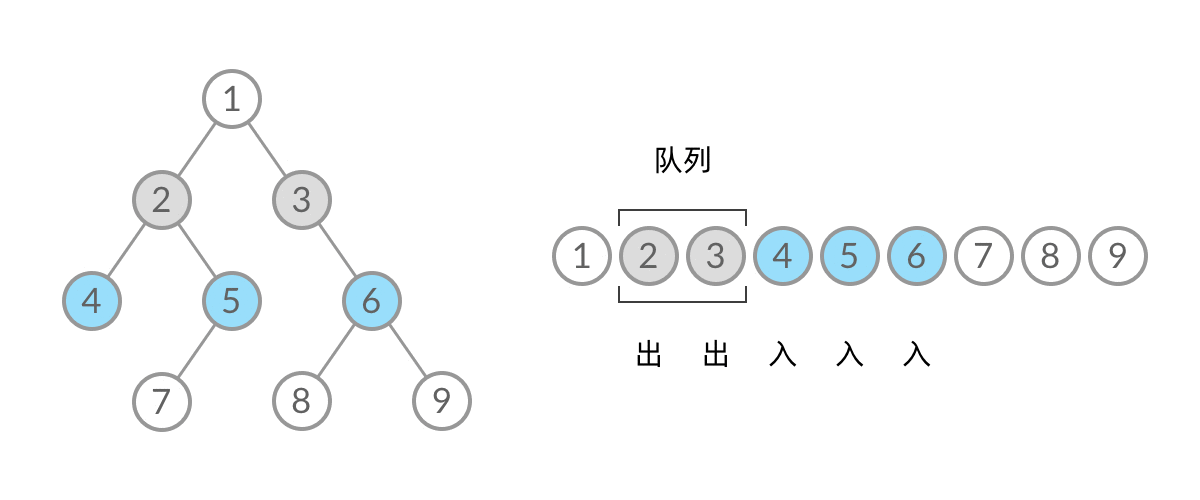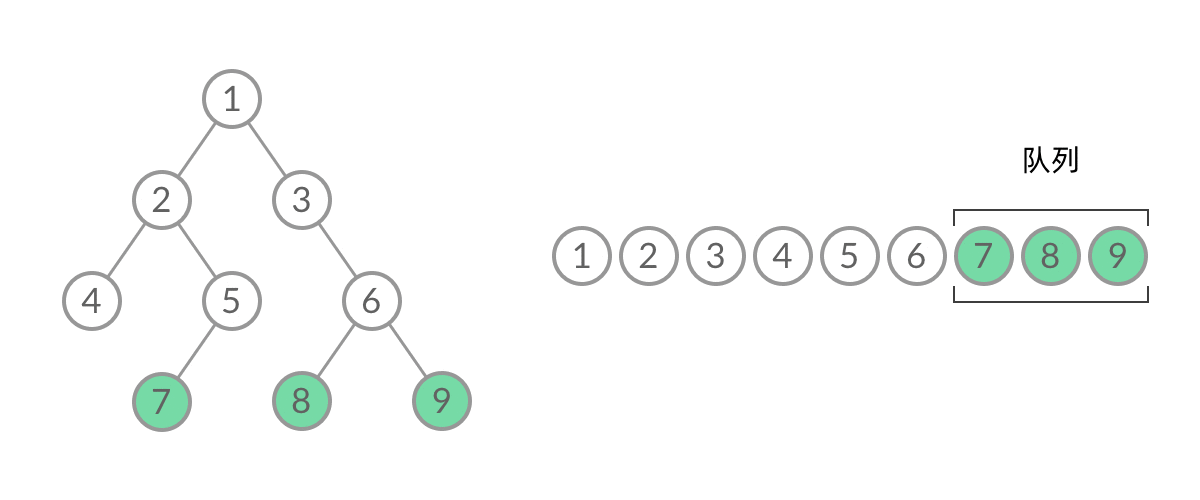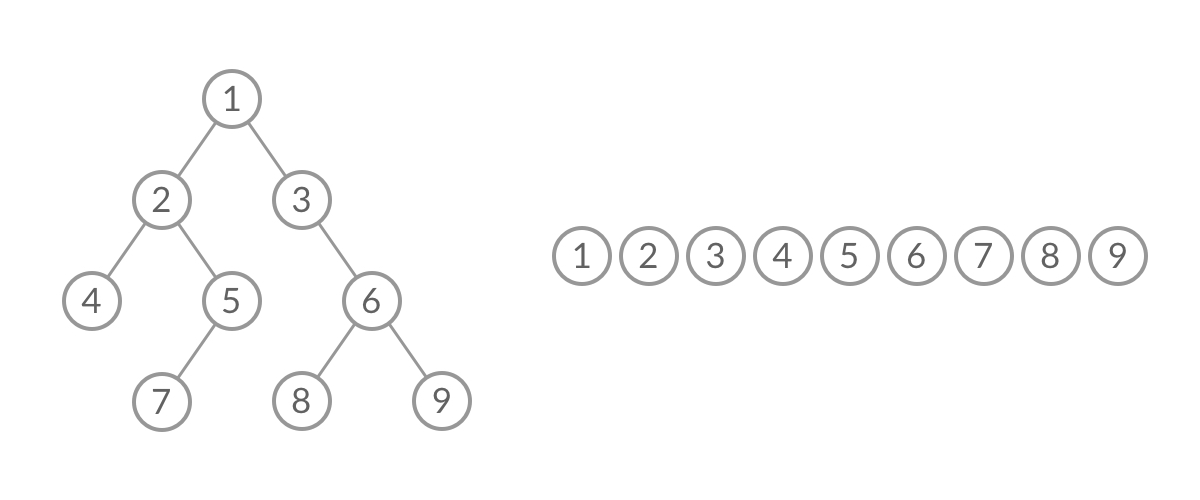
- ⬇️ 找到的认为最直观的图:
var levelOrder = function (root) {
const res = []; // 存放结果数组
if (root === null) return res;
// 声明队列,用于存储下一层需要遍历的结点
const queue = [];
queue.push(root);
// 遍历队列
while (queue.length !== 0) {
// 针对本轮操作,创建一个新的二维数组,对于本层找到的结点值都存储在该数组中。
res.push([]);
const len = queue.length; // 记录本层结点数
for (let i = 0; i < len; i++) {
// 将遍历过的结点出队
const curNode = queue.shift();
res[res.length - 1].push(curNode.val);
// 检测该结点是否存在左右子结点,有则入队,作为下一层的遍历结点
if (curNode.left) queue.push(curNode.left);
if (curNode.right) queue.push(curNode.right);
}
}
return res;
};
时间复杂度:O(n),n 为二叉树的结点数目,每一个结点入队出队各一次。
空间复杂度:O(n),n 为二叉树的结点数目,队列中存储的结点数目不超过 n 个。
94. 二叉树的中序遍历
方法一:递归
var inorderTraversal = function (root) {
const res = [];
const inorder = function (root) {
if (root === null) return;
inorder(root.left);
res.push(root.val);
inorder(root.right);
}
inorder(root);
return res;
};
时间复杂度:O(n),n 为二叉树的节点,每一个节点只被遍历一次。
空间复杂度:O(n),为递归过程中栈道开销,平均情况为O(logn),最坏情况为树呈现链状,为O(n)。
方法二:迭代
额外声明一个栈,迭代二叉树 如果当前结点不为空就把当前结点入栈,然后节点指向左子树进行迭代。 当迭代的右子树为空时,栈顶的第一个节点就是我们需要记录的第一个节点,出栈并记录。 然后节点指向右子树进行迭代。
// 写法一:
var inorderTraversal = function (root) {
const res = [];
const stack = [];
while (root !== null || stack.length !== 0) {
if (root !== null) {
stack.push(root);
root = root.left;
} else {
root = stack.pop();
res.push(root.val);
root = root.right;
}
}
return res;
};
// 写法二:
var inorderTraversal = function (root) {
const res = [];
const stack = [];
while (root !== null || stack.length !== 0) {
while (root !== null) {
stack.push(root);
root = root.left;
}
root = stack.pop();
res.push(root.val);
root = root.right;
}
return res;
};
时间复杂度:O(n),n 为二叉树的节点,每一个节点只被遍历一次。
空间复杂度:O(n),为迭代过程中显示栈道开销,平均情况为O(logn),最坏情况为树呈链状,为O(n)。
98. 验证二叉搜索树
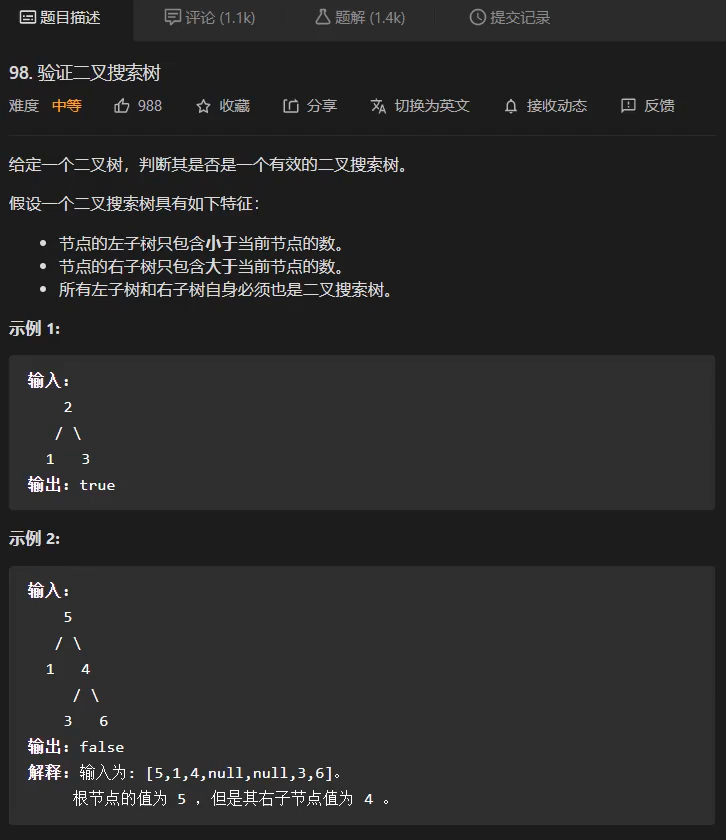
方法一:递归
额外定义一个辅助函数 boolean recurse(TreeNode node, int lower, int upper),参数分别为:
- 对于左子树 当前结点(curr) 当前结点的下限值(curr.left) 当前结点的上限值(root)
- 对于右子树 当前结点(curr) 当前结点的下限值(root) 当前结点的上限值(curr.right)
var isValidBST = function (root) {
return helper(root, -Infinity, Infinity);
};
const helper = function (root, lower, upper) {
if (root === null) return true;
// 检测当前结点值是否超过上下边界,超过返回false
if (root.val <= lower || root.val >= upper) return false;
// 没超过边界,检测左右子结点。
// 将当前结点的值作为上界对 node.left 进行递归
// 将当前结点的值作为下界对 node.right 进行递归
return helper(root.left, lower, root.val) && helper(root.right, root.val, upper);
}
时间复杂度:O(n),n 为二叉树的结点数目,在递归调用过程中每一个节点只被遍历一次。
空间复杂度:O(n),n 为二叉树的深度,递归函数需要栈空间,栈空间取决于递归的深度。
方法二:中序遍历
二叉搜索树「中序遍历」得到的值构成的序列一定是升序的,这启示我们在中序遍历的时候实时检查当前节点的值是否大于前一个中序遍历到的节点的值即可。
var isValidBST = function (root) {
const stack = [];
// 声明一个变量,记录当前操作结点,用于与下次获取的节点进行对比
let prev = -Infinity;
while (root !== null || stack.length !== 0) {
while (root !== null) {
stack.push(root);
root = root.left;
}
root = stack.pop();
// 如果中序遍历得到的节点的值小于等于前一个 prev,说明不是二叉搜索树,返回false
if (root.val <= prev) return false;
prev = root.val; // 存储当前结点的值作为下一个节点的比较对象
root = root.right;
}
return true;
};
时间复杂度:O(n),n 为二叉树的节点,每一个节点只被遍历一次。
空间复杂度:O(n),n 为二叉树的节点,栈栈最多存储 n 个节点。
笨方法:递归获取树结点数组
递归中序遍历二叉树,将二叉树转变成一个数组,判断结点数组是否是单调递增的,是返回 true。
var isValidBST = function (root) {
const arr = [];
// 递归函数
const inorder = function (root) {
if (root === null) return;
inorder(root.left);
arr.push(root.val); // 将二叉搜索树转换为有序数组
inorder(root.right);
}
inorder(root);
// 判断是否递增
let isasc = true;
for (let i = 1; i < arr.length; i++) {
if (arr[i] <= arr[i - 1]) isasc = false;
}
return isasc;
};