Big O notation

大O表示法：我们讲算法执行运算大操作数丢弃掉低阶项，再去掉所有的系数，在它前面加上一个O，就是大O表示法。

  • O(1)：Constant Complexity 常数复杂度
  • O(log n)：Logarithmic Complexity 对数复杂度
  • O(n)：Linear Complexity 线性时间复杂度
  • O(n^2)：N square Complexity 平方
  • O(n^3)：N cubic Complexity 立方
  • O(2^n)：Exponential Growth 指数
  • O(n!)：Factorial 阶乘

一些简单的例子

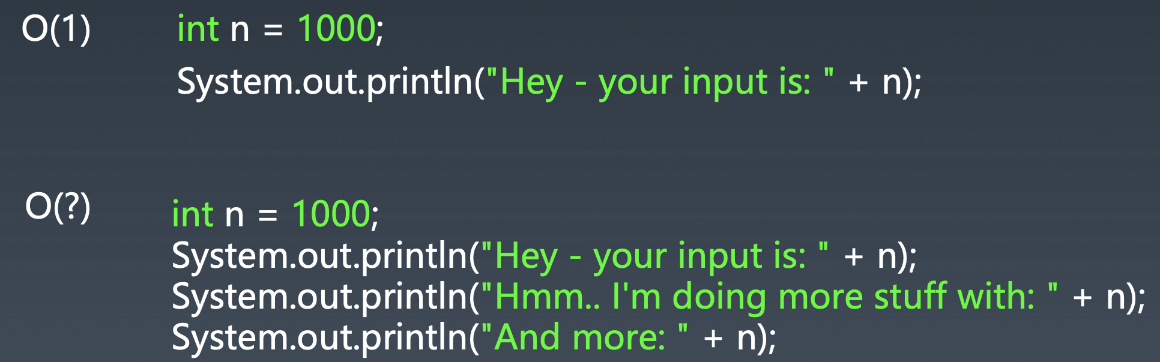
image.png
1 2段代码无论n为多少，分别都只执行1次和3次，也就是O(1)和O(3)，但是我们都统称为 O(1) ，因为它们都是 常数级 的 ，但是面试的时候都要说是 O(1)或者叫常数时间复杂度 。

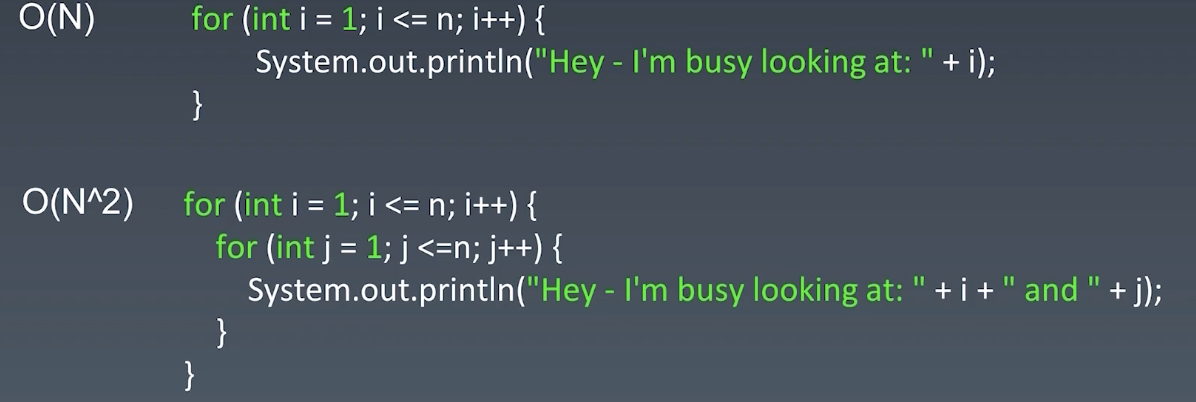
image.png
1 段代码随着n的不同，这段代码它执行的次数也会不一样。他的时间复杂度和n是成线性关系，所以我们记为 O(n) 。假设n为多少的话，它的执行速度，执行次数，运行复杂度就是n的一次方，所以叫做O(n)线性的时间复杂度。
同理，2段代码是嵌套型的循环，如果n=100，我们会看到System.out.printIn执行了100100=10000次，所以它的时间复杂度就是 O(n^2) 。
思考：若2 段代码 这两个循环不是嵌套的，而是并列的执行，那么它的时间复杂度是多少呢？
*答案：即使它们是并列的，那么就相当于2n次，前面的常数系数我们不关系，就是O(n)的时间复杂度

image.png
1段代码，执行次数是log2(n)，所以他的时间复杂度是 O(log n) 。
2段代码，求Fibonacci数列的第n项是多少。这就是牵扯到递归程序在执行的时候，怎么计算它的时间复杂度。答案是 k^n ，这里的k是一个常数，它是指数级的。

时间复杂度曲线图

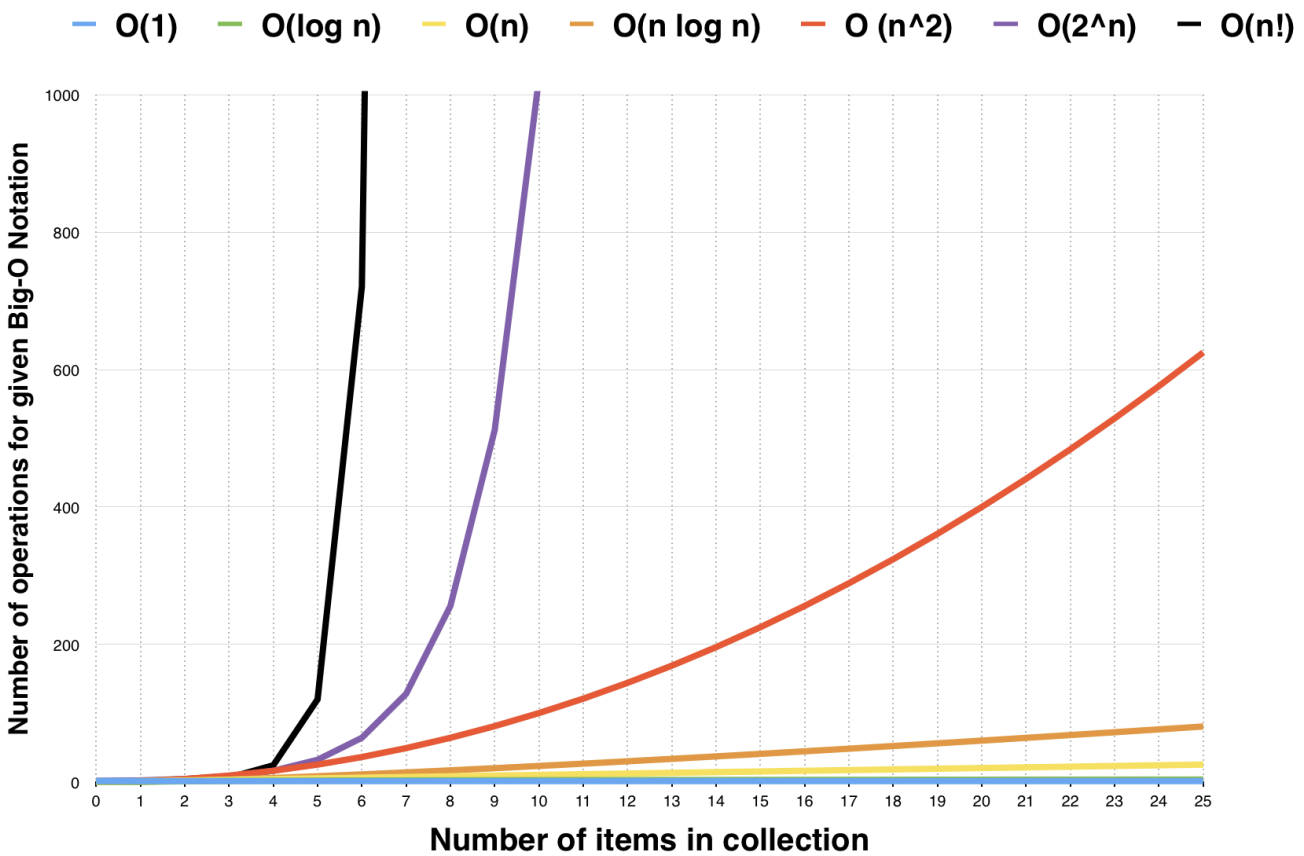
image.png

不同程序在写法当中，完成同样的目标，它可能会导致时间复杂度的不同。一个简单例题感受一下：

从1加到2一直加到n的话它的求和。

  • 暴力解法：从1到n的循环累加。

时间复杂度：O(n) 一重循环，n值即为循环次数

  1. let y = 0
  2. for i = 1 to n:
  3.     y += i
  • 数学求和公式：sum = n (n+1) / 2

时间复杂度：O(1) 常数时间复杂度 这段代码用于只执行一次

y = n * (n + 1) / 2

递归条件下分析时间复杂度

关键：了解递归总共执行了语句多少次。
借助递归状态的状态树（把递归的执行顺序，画出一个树型结构）
我们通过 求Fibonacci数列的第n项
Fib-> 0, 1, 1, 2, 3, 5, 8, 13, 21, …

F(n) = F(n - 1) + F(n - 2)
  • 递归
    int fib (int n){
  if(n < 2) return n;
  return fib(n - 1) + fib(n - 2);
}
    假设 n = 6，要算F(6)就要算F(5)和F(4)，此时多出了两次运算，再接下去算F(5)和F(4)，此时我们可以发现两个现象。
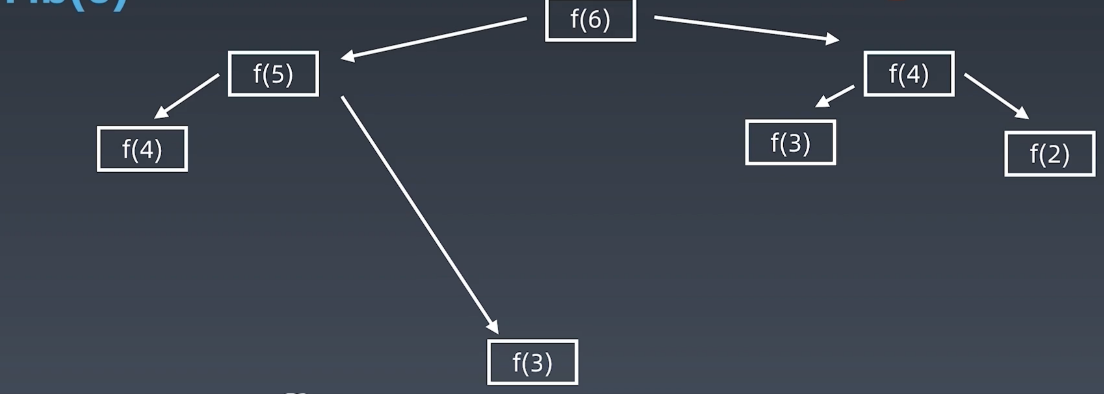
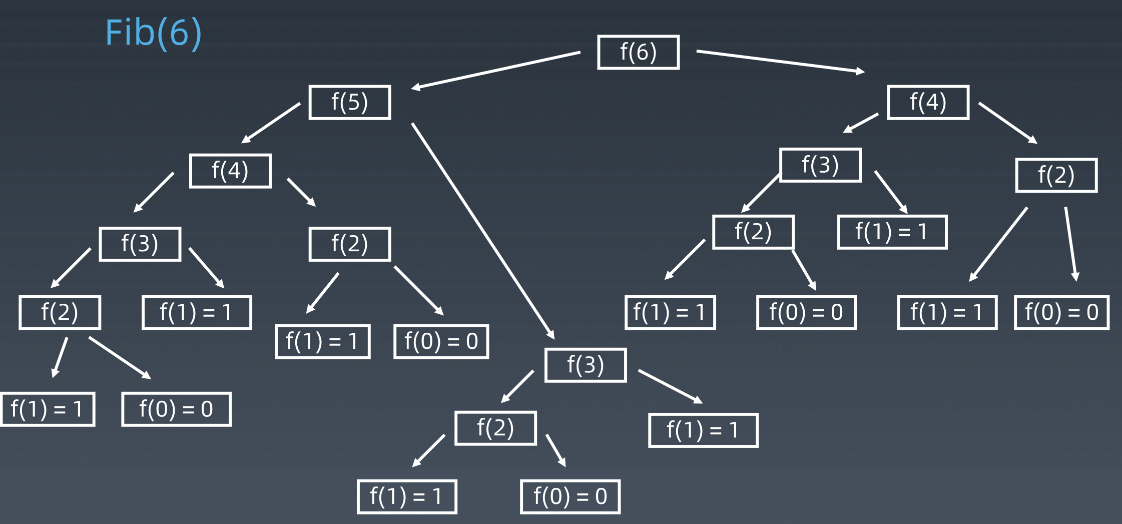
    image.png
    image.png
  1. 它每多展开一层，运行的节点数就是上面一层的两倍。所以每一层的节点数也就是它的执行次数是按指数级递增的。由此可见，在最后一层时就变成了2^n
  2. 有重复的节点出现在我们执行的状态树里，我们会发现F3、F2、F1被计算了很多次。就是因为有这么多冗余的计算，导致求Fibonacci数的第6项，变成了2^6这么一个繁复的时间复杂度

Master Theorem主定理

主定理，用来解决所有递归的函数，怎么计算它的时间复杂度

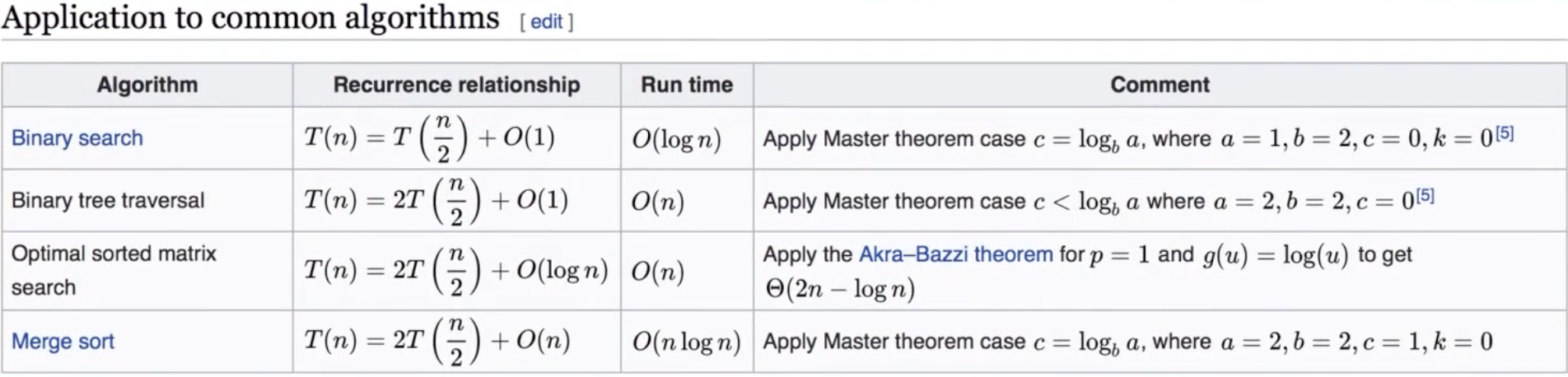
image.png

思考：

  1. 二叉树便利 - 前序、中序、后序：时间复杂度是多少？
    1. O(N) N代表二叉树里面的数的节点总数
  2. 图的遍历：时间复杂度是多少？
    1. O(N) N代表图的里面的节点总数
  3. 搜索算法：DFS、BFS 时间复杂度是多少？
    1. O(N) N代表搜索空间里面的节点总数
  4. 二分查找：时间复杂度是多少？
    1. O(logN) N代表？？？？？？

空间复杂度

分析空间复杂度和时间复杂度的情况类似，但是它更加简单。
遵循两个主要原则：

  1. 数组的长度。
    1. 如果你的代码里开了数组，那么数组的长度基本上就是你的空间复杂度。一维数组长度为n，则空间复杂度为O(n)，二维数组长度为n^2空间复杂度为O(n^2)
  2. 递归的深度。
    1. 如果你的代码里有递归，那么递归最深的深度就是你的空间复杂度的最大值
    2. 如果你的代码又是递归里面又开了数组，那么两者之间的最大值就是你的空间复杂度

例题LC.70爬楼梯

从 Climbing Stairs 这题不同的解法分析它不同的时间和空间复杂度。
这题的通项公式就是Fibonacci的公式
- 第1级台阶：1种方法（爬 1 级）
- 第2级台阶：2种方法（爬 1 级或爬 2 级）
- 第n级台阶：从第 n-1 级台阶爬1级或从第 n-2 级台阶爬2级
台阶数：1，2，3，4，5
方法数：1，2，3，5，8

F(n) = F(n - 1) + F(n - 2)

image.png

方法1：暴力解法 递归

class Solution {
    public int climbStairs(int n) {
        if(n==1){
            return 1;
        }
        if(n==2){
            return 2;
        }
        return climbStairs(n-1)+climbStairs(n-2);
    }
}

在 n=5 时的递归树是这样的：

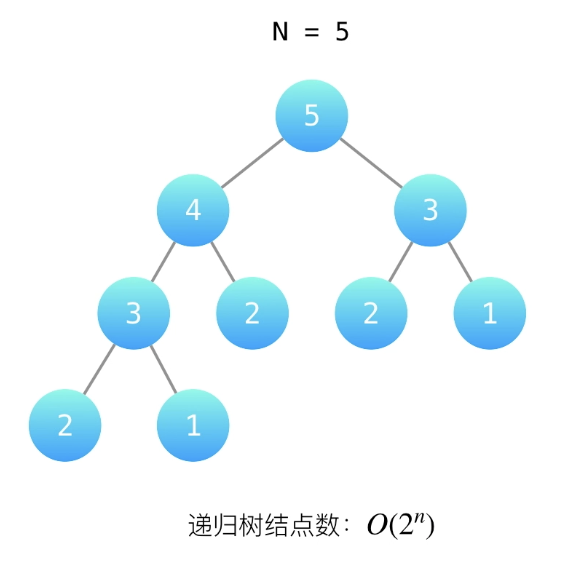
image.png
递归数深度为n，所以空间复杂度为 O(n)
递归树有2^n个结点，所以时间复杂度为 O(2^n)

方法2：记忆化递归

使用memo存储中间结果，避免重复计算。

class Solution {
    public int climbStairs(int n) {
        int memo[]=new int[n + 1];
        return climbStairsMemo(n,memo);
    }
    public int climbStairsMemo(int n,int memo[]){
        if(memo[n]>0){
            return memo[n];
        }
        if(n == 1){
            memo[n] = 1;
        }else if(n == 2){
            memo[n] =2;
        }else{
            memo[n] = climbStairsMemo(n - 1,memo) + climbStairsMemo(n - 2,memo);
        }
        return memo[n];
    }
}

当递归爬到n级台阶的时，如果这个n级台阶的方法已经计算过了就直接返回memo中的保存的结果。这样我们就可以保证爬到各级台阶的方法只被计算了一次，从而将时间复杂度优化到 O(n)
虽然它递归状态减少了，但是他多了一个memo数组，这个数组的长度为n，所以它的空间复杂度还是 O(n)

方法3：动态规划

不难发现，这个问题可以被分解为一些包含最优子结构的子问题，即它的最优解可以从其子问题的最优解来有效地构建，我们可以使用动态规划来解决这一问题。

第 i 阶可以由一下两种方法得到：

  1. 在第(i - 1)阶后向上爬1阶。
  2. 在第(i - 2)阶后向上爬2阶。

所以到达第 i 阶第方法总数就是到第(i - 1)阶和第(i - 2)阶的方法之和。
令dp[i]表示能到达第i阶的方法总数：
dp[i] = dp[i - 1] + dp[i - 2]

class Solution {
    public int climbStairs(int n) {
        if(n==1){
            return 1;
        }
        int[] dp = new int[n + 1];
        dp[1] = 1;
        dp[2] = 2;
        for(int i = 3;i <= n;i++){
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

代码中开来dp这个数组数组长度为 n+1 ，所以空间复杂度为 O(n) 。
循环了n次，所以时间复杂度为 O(n)

方法4：滚动数组

观察动态规划的代码，dp中存储了全部n个状态，但是只有两个状态会在更新下一个状态的过程中被使用到，如果只记录这两个状态我们就可以将空间复杂度从 O(n) 降到 O(1) 

public class Solution{
    public int climbStairs(int n){
        if(n==1){
            return 1;
        }
        int first = 1;
        int second = 2;
        for(int i = 3;i <= n;i++){
            int third = first + second;
            first = second;
            second = third;
        }
        return second;
    }
}
  • 时间复杂度：O(n) ，单循环到n，需要计算第n个斐波那契数
  • 空间复杂度：O(1) ，使用常量级空间。