概念
单调栈(Monotone Stack)是指:栈中元素之间的关系具有单调性,元素只能通过栈顶进出,且遵循先进后出的逻辑顺序。
单调递增栈:从栈底到栈顶元素是从小到大
单调递减栈:从栈底到栈顶元素是从大到小
- 单调递增栈,利用波谷剔除栈中的波峰,留下波谷;
- 单调递减栈,利用波峰剔除栈中的波谷,留下波峰;
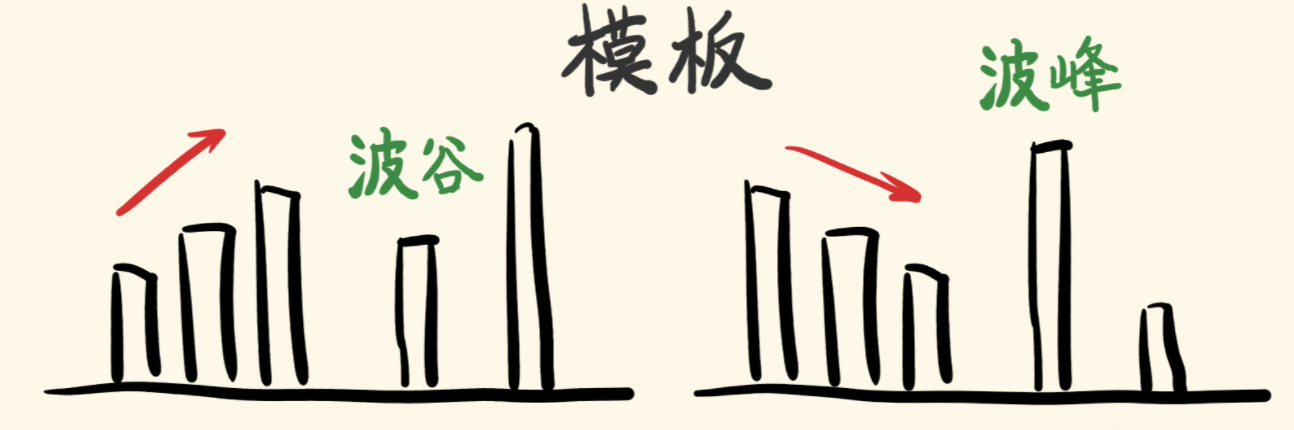
用单调栈来解决的问题一般都是:一维数组,要寻找任一元素右边(左边)第一个比自己大(小)的元素。
栈是辅助的数据结构,保存了我们在遍历过程中的信息,后面看到的数据优于之前看到的数据,计算出结果,以后进先出的形式完成计算,使用栈是典型的空间换时间思想的体现,学习数据结构和算法的意义就在于此,通过使用恰当的符合问题场景的数据结构和算法,加快了我们计算的时间效率,避免了重复的计算。
建立模板
给你一个数组nums,请你返回一个等长的结果数组,结果数组中对应下标存储着下一个更大(下一个更小、上一个更大、上一个更小)元素,如果没有就存储-1。
辅助函数
为代码更具清晰明了添加的辅助函数,不如代码会有点长不好理解
Array.prototype.top = function () {return this[this.length - 1]}Array.prototype.empty = function () {return !this.length}// 用于代替// !stack.length// stack[stack.length-1]
下一个更大元素
/**
* @param {number[]}nums
* @return {number[]}
*/
// 正向遍历
var nextGreaterElement_1 = function (nums) {
const res = new Array(nums.length).fill(-1); // 存放结果数组 默认值为-1表示没有找到
const stack = []; // 单调递减栈 保证栈中元素未找到下一个更大元素(存放索引)
for (let i = 0; i < nums.length; i++) {
// 栈中有值 且 当前元素大于栈顶元素,说明栈中部分元素的下一个更大元素已找到,需要记录并弹栈
// [4,2,1] current->3
while (!stack.empty() && nums[i] > nums[stack.top()]) {
res[stack.top()] = nums[i];
stack.pop();
}
stack.push(i);
}
return res;
}
- 懒人福音 ⬇️⬇️⬇️ 看这一个就好了 ⬇️⬇️⬇️
/**
* @param {number[]}nums
* @return {number[]}
*/
// 逆向遍历(相较正向遍历清晰很多)
var nextGreaterElement_2 = function (nums) {
const res = new Array(nums.length); // 存放结果数组
const stack = []; // 单调递减栈,保证栈顶元素即是当前元素下一个更大元素
for (let i = nums.length - 1; i >= 0; i--) {
// 栈中有值 且 当前元素 大于等于 栈顶元素 则弹栈
while (!stack.empty() && nums[i] >= stack.top()) {
// 矮个子起开,反正也被挡着
stack.pop();
}
// 此时栈顶元素就是当前元素元素下一个更大元素,提前是栈中有值
res[i] = stack.empty() ? -1 : stack.top();
// 压栈
stack.push(nums[i]);
}
return res;
}
下一个更小元素
/**
* @param {number[]}nums
* @return {number[]}
*/
// 正向遍历
var nextLesserElement_1 = function (nums) {
const res = new Array(nums.length).fill(-1); // 存放结果数组 默认值为-1表示没有找到
const stack = []; // 单调递增栈,保证栈中元素为找到下一个更小元素(存放索引)
for (let i = 0; i < nums.length; i++) {
// 栈中有值 且 当前元素 小于 栈顶元素,说明栈中部分元素的下一个更小元素已经找到,需要记录并弹栈
while (!stack.empty() && nums[i] < nums[stack.top()]) {
res[stack.top()] = nums[i];
stack.pop();
}
stack.push(i);
}
return res;
}
/**
* @param {number[]}nums
* @return {number[]}
*/
// 逆向遍历(相较正向遍历清晰很多)
var nextLesserElement_2 = function (nums) {
const res = new Array(nums.length); // 存储结果数组
const stack = []; // 单调递增栈,保证栈顶元素即是当前元素下一个更小元素
for (let i = nums.length - 1; i >= 0; i--) {
// 栈中有值 且 当前元素 小于等于 栈顶元素 则弹栈
while (!stack.empty() && nums[i] <= stack.top()) {
stack.pop();
}
// 此时栈顶元素就是当前元素下一个更小元素,提前是栈中有值
res[i] = stack.empty() ? -1 : stack.top();
// 压栈
stack.push(nums[i]);
}
return res;
}
上一个更大元素
/**
* @param {number[]}nums
* @return {number[]}
*/
// 正向遍历(相较逆向遍历清晰很多)
var lastGreaterElement_1 = function (nums) {
const res = new Array(nums.length); // 存放结果数组
const stack = []; // 单调递减栈,保证栈顶元素即是当前元素上一个更大元素
for (let i = 0; i < nums.length; i++) {
// 栈中有值 且 当前元素 大于等于 栈顶元素 则弹栈
while (!stack.empty() && nums[i] >= stack.top()) {
stack.pop()
}
// 此时有栈顶元素即使当前元素上一个更大元素,前提是栈中有值
res[i] = stack.empty() ? -1 : stack.top();
// 压栈
stack.push(nums[i]);
}
return res;
}
/**
* @param {number[]}nums
* @return {number[]}
*/
// 逆向遍历
var lastGreaterElement_2 = function (nums) {
const res = new Array(nums.length).fill(-1); // 存放结果数组
const stack = []; // 单调递减栈,保证栈中元素未找到上一个更大元素(存索引)
for (let i = nums.length - 1; i >= 0; i--) {
// 栈中有值 且 当前元素 大于 栈顶元素 ,说明栈中部分元素上一更大元素已找到,需要记录并弹栈
while (!stack.empty() && nums[i] > nums[stack.top()]) {
res[stack.top()] = nums[i];
stack.pop();
}
stack.push(i);
}
return res;
}
上一个更小元素
// 上一个更小元素
/**
* @param {number[]}nums
* @return {number[]}
*/
// 正向遍历(相较逆向遍历清晰很多)
var lastLesserElement_1 = function (nums) {
const res = new Array(nums.length); // 存放结果数组
const stack = []; // 单调递增栈,保证栈顶元素即使当前元素上一个更小元素
for (let i = 0; i < nums.length; i++) {
// 栈中有值 且 当前元素 小于等于 栈顶元素 则弹栈
while (!stack.empty() && nums[i] <= stack.top()) {
stack.pop();
}
// 此时有栈顶元素即是当前元素上一个更小元素,前提是栈中有值
res[i] = stack.empty() ? -1 : stack.top();
// 压栈
stack.push(nums[i]);
}
return res;
}
/**
* @param {number[]}nums
* @return {number[]}
*/
// 逆向遍历
var lastLesserElement_2 = function (nums) {
const res = new Array(nums.length).fill(-1); // 存放结果数组
const stack = []; // 单调递增,保证栈中元素未找到上一个更小元素(存放索引)
for (let i = nums.length - 1; i >= 0; i--) {
// 栈中有值 且 当前元素 小于 栈顶元素,说明栈中部分元素的下一个更大元素已经找到,需要记录并弹栈
while (!stack.empty() && nums[i] < nums[stack.top()]) {
res[stack.top()] = nums[i];
stack.pop();
}
stack.push(i);
}
return res;
}
总结:
第一个大元素就单调递减栈,第一个小元素就单调递增栈 左边第一个就从左向右正向遍历,右边第一个就从右向左逆向遍历

下一个更大(更小)关注点在当前元素的右边,所以我们从右边开始遍历,维护一个单调递减(递增)栈,保证栈顶元素即是当前元素的目标元素。
上一个更大(更小)关注点在当前元素的左边,所以我们从左边开始遍历,维护一个单调递减(递增)栈,保证栈顶元素即是当前元素的目标元素。
- 左边第一个大 从左向右遍历 单调递减
- 右边第一个大 从右向左遍历 单调递减
- 左边第一个小 从左向右遍历 单调递增
- 右边第一个小 从右向左遍历 单调递增
复杂度分析:
这个算法的时间复杂度不是那么直观,如果你看到 for 循环嵌套 while 循环,可能认为这个算法的复杂度也是 O(n^2) ,但实际上这个算法但复杂度只有 O(n) 。
分析它的时间复杂度,要从整体来看:总共有 n 哥元素,每个元素都被 push 入栈了一次,而最多被 pop 一次 ,没有任何冗余操作。所以总都计算规模是和元素规模 n 成正比的,也就是 O(n) 的复杂度。
经典使用
题目:LC496.下一个更大元素I

暴力解法
- 遍历nums1,寻找当前元素在nums2中的位置,然后寻找当前元素在nums2中的下一个更大元素
var nextGreaterElement = function (nums1, nums2) {
let res = new Array(nums1.length).fill(0);
for (let i = 0; i < nums1.length; i++) {
// 寻找nums1中元素在nums2中对应的位置
let targetIndex = 0; // 储存nums1[i]在 nums2中的下标
while (targetIndex < nums2.length && nums1[i] !== nums2[targetIndex]) {
targetIndex++;
}
// 寻找下一个更大元素
let nextIndex = targetIndex + 1;
while (nextIndex < nums2.length && nums2[nextIndex] < nums2[targetIndex]) {
nextIndex++;
}
// 判断存不存在并存储相应结果
// nextIndex小于nums2.length 或 nums2[nextIndex] > nums2[targetIndex]
res[i] = nextIndex < nums2.length ? nums2[nextIndex] : -1;
}
return res;
};
时间复杂度:O(mn),其中m是nums1的长度,n是nums2的长度
空间复杂度:O(1)
单调栈+哈希表(正向遍历)
从左向右正向遍历nums2,维护一个单调栈(单调递减),当遇到大于栈顶的元素时,此元素就是栈中小于该元素的下一个更大元素,需要出栈并且记录哈希表中。
var nextGreaterElement = function (nums1, nums2) {
const dic = new Map(); // 哈希表 键为nums2中的元素 值为该元素下一个更大元素
const stack = []; // 单调递减 保证栈中元素未找到下一个更大元素
for (let i = 0; i < nums2.length; i++) {
// 栈中有值 且 当前元素大于栈顶元素,说明栈中部分元素的下一个更大元素已找到,需要弹栈
while (stack.length && nums2[i] > stack[stack.length - 1]) {
dic.set(stack[stack.length - 1], nums2[i]);
stack.pop();
}
// 压栈
stack.push(nums2[i]);
}
// 此时哈希表建设完毕,返回结果元素 两种方法⬇️
// const res = new Array(nums1.length).fill(0).map((_, i) => {
// if(dic.has(nums1[i])){
// return dic.get(nums1[i]);
// }else{
// return -1;
// }
// });
const res = [];
for (let i = 0; i < nums1.length; i++) {
res[i] = dic.get(nums1[i]) || -1;
}
return res;
};
时间复杂度:O(m+n),其中m是nums1的长度,n为nums2的长度。我们需要遍历nums2以计算nums2中每个元素右边的第一个更大元素,需要遍历nums1以生成查询结果。
空间复杂度:O(n),用于存储哈希表
最优 - 单调栈+哈希表(逆向遍历)
从右向左逆向遍历,维护一个单调栈(单调递减),当遇到大于(数组不重复,重复就是大于等于)栈顶元素时,进行弹栈,此时栈顶元素即是当前元素的下一个更大元素(栈中有值),使用哈希表记录后压栈。
var nextGreaterElement = function (nums1, nums2) {
const dic = new Map();
const stack = [];
for (let i = nums2.length - 1; i >= 0; i--) {
// 栈中有值 且 当前元素 大于 栈顶元素 则弹栈
while (stack.length && nums2[i] > stack[stack.length - 1]) {
stack.pop();
}
// 此时栈顶元素及时当前元素下一个更大元素,前提是栈中有值。用哈希表保存
dic.set(nums2[i], stack[stack.length - 1] || -1);
// 压栈
stack.push(nums2[i]);
}
// 此时哈希表建设完毕,返回结果值。
const res = new Array(nums1.length).fill(0).map((_, i) => dic.get(nums1[i]));
return res;
};
时间复杂度:O(m+n),其中m是nums1的长度,n为nums2的长度。我们需要遍历nums2以计算nums2中每个元素右边的第一个更大元素,需要遍历nums1以生成查询结果。
空间复杂度:O(n),用于存储哈希表
题目:LC739.每日温度
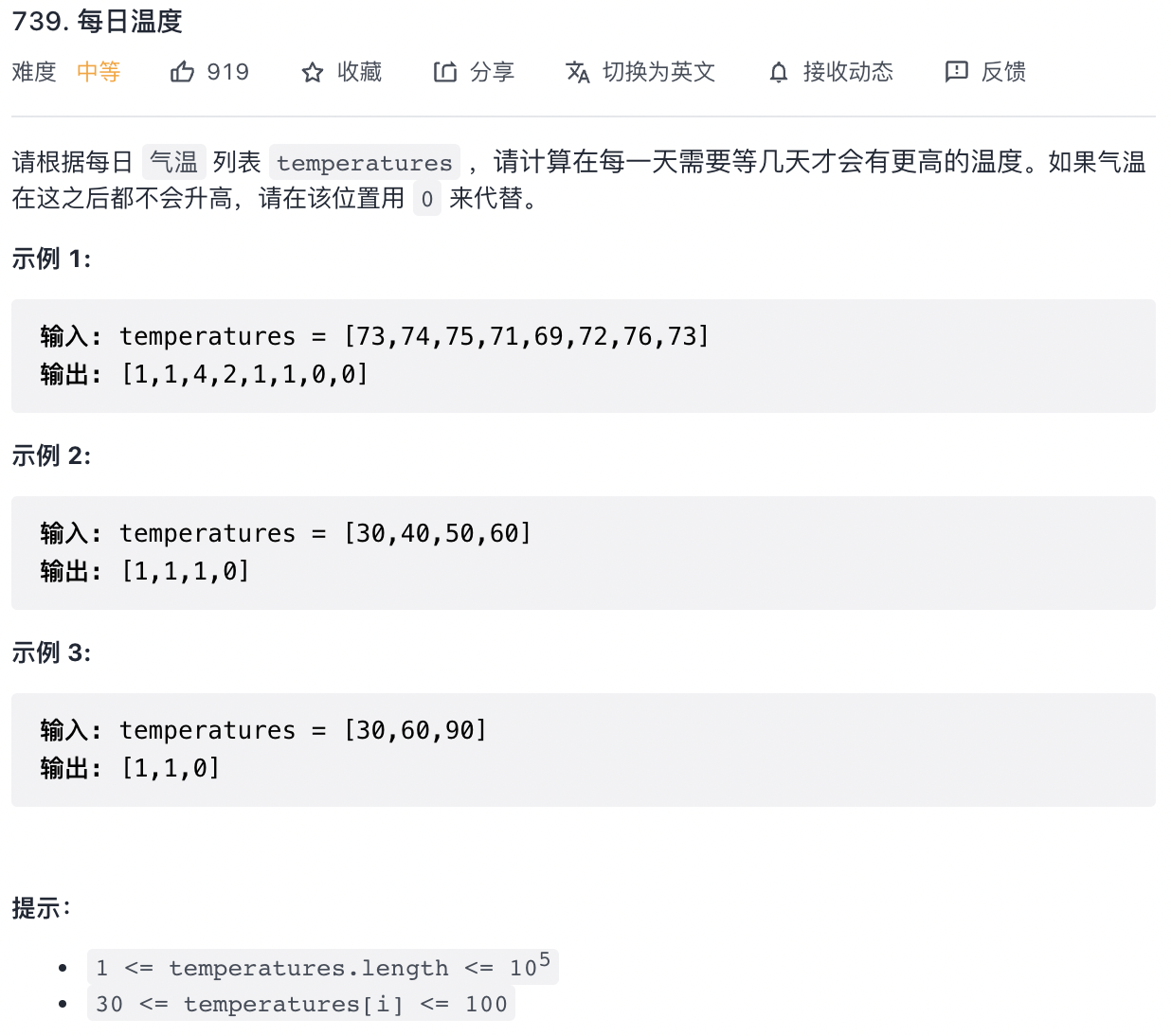
暴力解法
- 双重 for 循环如果匹配到大于当天的,就把相差的天数放入返回的数组,并跳出循环
var dailyTemperatures = function (temperatures) {
let ans = new Array(temperatures.length).fill(0);
for (let i = 0; i < temperatures.length; i++) {
for (let j = i + 1; j < temperatures.length; j++) {
if (temperatures[i] < temperatures[j]) {
ans[i] = j - i;
break;
}
}
}
}
单调栈(正向遍历)
var dailyTemperatures = function (temperatures) {
const res = new Array(temperatures.length).fill(0);
const stack = []; // 单调递减,存储温度列表的下标,保证栈中元素未找到下一个更大元素
for (let i = 0; i < temperatures.length; i++) {
// 单调栈中有值 且 栈顶下标对应的元素 小于 当前元素 ,说明栈中部分元素下一个更大元素以及找到-> 出栈
while (stack.length && temperatures[stack[stack.length - 1]] < temperatures[i]) {
let previousIndex = stack.pop();
res[previousIndex] = i - previousIndex;
}
stack.push(i);
}
return res;
};
单调栈(逆向遍历)
var dailyTemperatures = function (temperatures) {
// 维护一个单调递减的栈,栈顶就是当前项右边第一个大元素
const res = new Array(temperatures.length).fill(0);
const stack = []; // 单调递减 存储温度列表的下标 保证栈顶元素即使当前元素下一个更大元素
// 逆向遍历
for (i = temperatures.length - 1; i >= 0; i--) {
// 如果单调栈中有值 且 栈顶元素 小于等于 当前项 -> 弹栈
while (stack.length && temperatures[stack[stack.length - 1]] <= temperatures[i]) {
stack.pop();
}
// 此时有栈顶下标对应的元素即为当前项下一个更大值
res[i] = stack.length ? stack[stack.length - 1] - i : 0;
// 压栈
stack.push(i);
}
return res;
}
题目:LC907.子数组的最小值之和
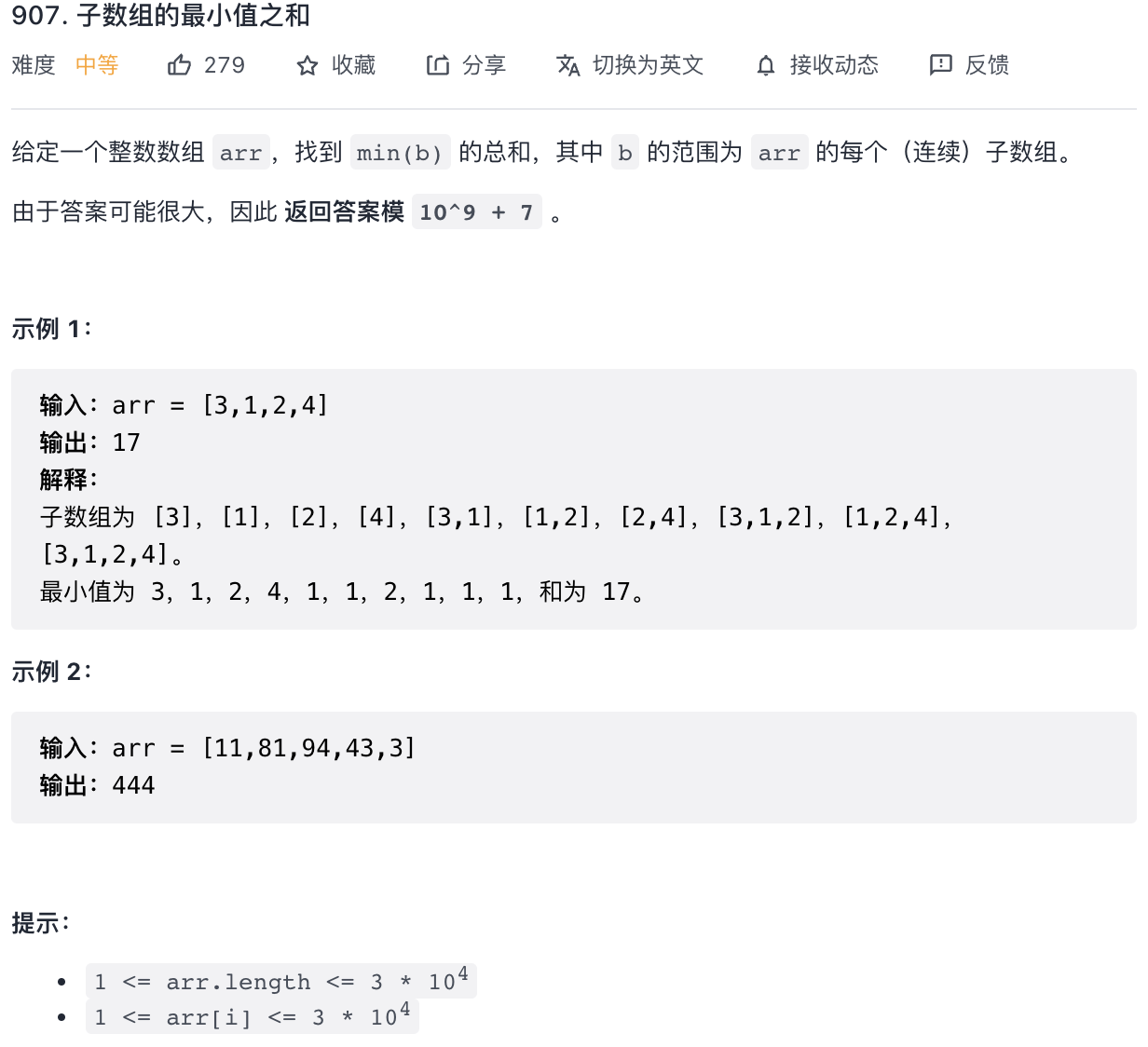
暴力解法
var sumSubarrayMins = function (arr) {
let res = 0;
for (let i = 0; i < arr.length; i++) {
let min_ = Infinity;
for (let j = i; j < arr.length; j++) {
min_ = Math.min(min_, arr[j]);
res += min_;
}
}
return res % (1e9 + 7);
};
时间复杂度:O(n^2)
空间复杂度:O(1)
单调栈+贡献值
对于一个数字 arr[i] 来说,如果在某个区间 [j, k] 里面它是最小值,那么 [j, k] 包含 arr[i] 的子数组的最小值也一定是 arr[i] 。所以我们只需要找出最大的那个区间,使得 arr[i] 是最小值就行了。
比如 [2,4,1,2] ,以1 为最小数。能构成的数组数为 (2+1)(1+1) ,2 表示 1 左面有两个比它大的数,1 表示 1 右面有一个比它大的数。
contribution = value amount
= value (currentIndex - expandLeft)(expandRight - currentIndex)
var sumSubarrayMins = function (arr) {
const stack = []; // 单调递增栈
const expandLeft = []; // 每个元素的左扩张边界
const expandRight = []; // 每个元素的右扩张边界
// step1 寻找左边扩张边界(寻找左边第一个小)
for (let i = 0; i < arr.length; i++) {
while (stack.length && arr[i] <= arr[stack[stack.length - 1]]) stack.pop();
// 此时有栈顶元素即是当前元素左边第一个更小元素
expandLeft[i] = stack.length ? stack[stack.length - 1] : -1;
stack.push(i);
}
// step2 - 寻找右扩张边界(寻找右边第一个小)
stack.length = 0; // stack初始化
for (let i = arr.length - 1; i >= 0; i--) {
// 此处选择 < 而不是 <= ,避免重复区间
while (stack.length && arr[i] < arr[stack[stack.length - 1]]) stack.pop();
// 此时有栈顶元素即使当前元素右边第一个更小元素
expandRight[i] = stack.length ? stack[stack.length - 1] : arr.length;
stack.push(i);
}
// step3 - 套用贡献值公式计算结果
let sum = 0;
for (let i = 0; i < arr.length; i++) {
sum += arr[i] * (i - expandLeft[i]) * (expandRight[i] - i);
}
return sum %= 1e9 + 7;
}
时间复杂度:O(N),其中 N 是 arr 的长度。
空间复杂度:O(N)。
单调栈+DP动态规划
知乎
博客院
力扣解答
dp(i) 表示以第i个结尾的子数组最小值之和,那么我们有转移方程:
dp(i) = (i - j) * A[i] + dp(j),j 是满足 A[x] < A[i] 且 x < i 的最大的 x(即i往左找第一个比A[i]小的数的序号)

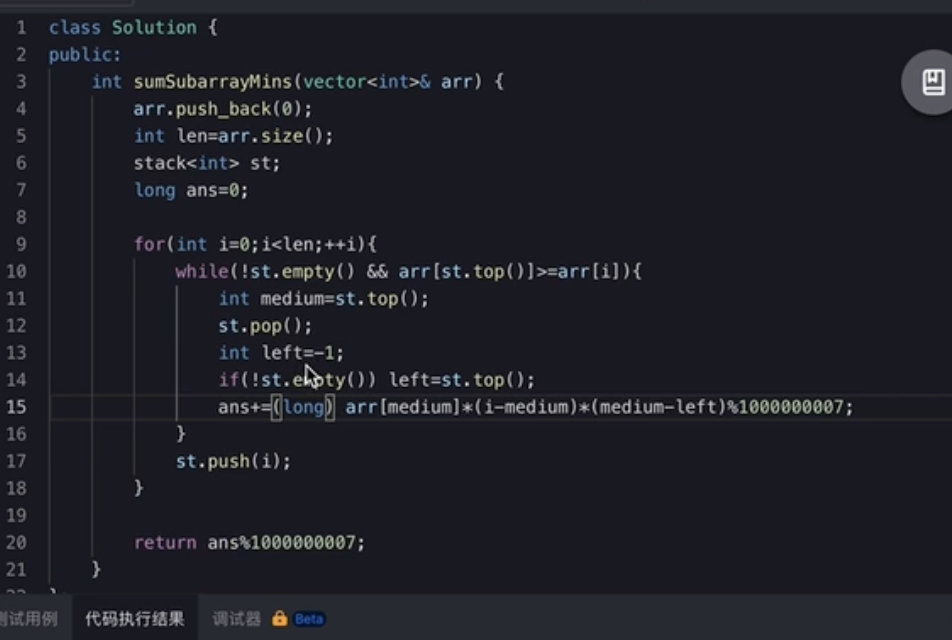
var sumSubarrayMins = function (arr) {
const stack = []; // 单调栈
stack.push(-1);
const DP = new Array(arr.length + 1).fill(0);
let sum = 0;
for (let i = 0; i < arr.length; i++) {
while (stack[stack.length - 1] !== -1 && arr[i] <= arr[stack[stack.length - 1]]) stack.pop();
// 此时有栈顶元素即是当前元素左边第一个更小元素
DP[i + 1] = DP[stack[stack.length - 1] + 1] + (i - stack[stack.length - 1]) * arr[i];
stack.push(i);
sum += DP[i + 1];
}
return sum %= 1e9 + 7;
}
时间复杂度:O(N),N为 arr 的长度。
空间复杂度:O(N),
单调栈+DP动态规划 2
var sumSubarrayMins = function (arr) {
const stack = []; // 单调栈
const DP = new Array(arr.length).fill(0);
let sum = 0;
for (let i = 0; i < arr.length; i++) {
while (stack.length && arr[i] <= arr[stack[stack.length - 1]]) stack.pop();
// 此时有栈顶元素即是当前元素左边第一个更小元素
if (stack.length) {
DP[i] = DP[stack[stack.length - 1]] + (i - stack[stack.length - 1]) * arr[i];
} else {
DP[i] = (i + 1) * arr[i];
}
stack.push(i);
sum += DP[i];
}
return sum %= 1e9 + 7;
}
题目:LC84.柱状图中最大的矩形
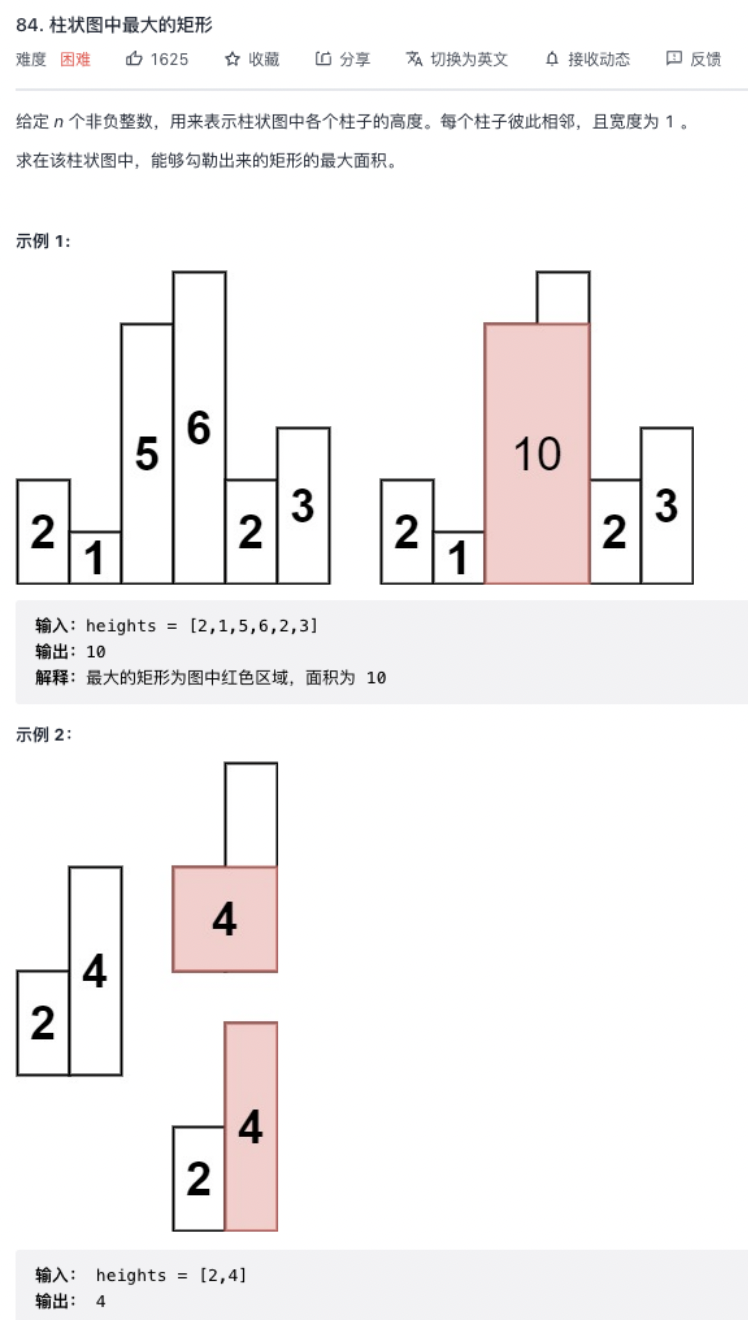
暴力解法
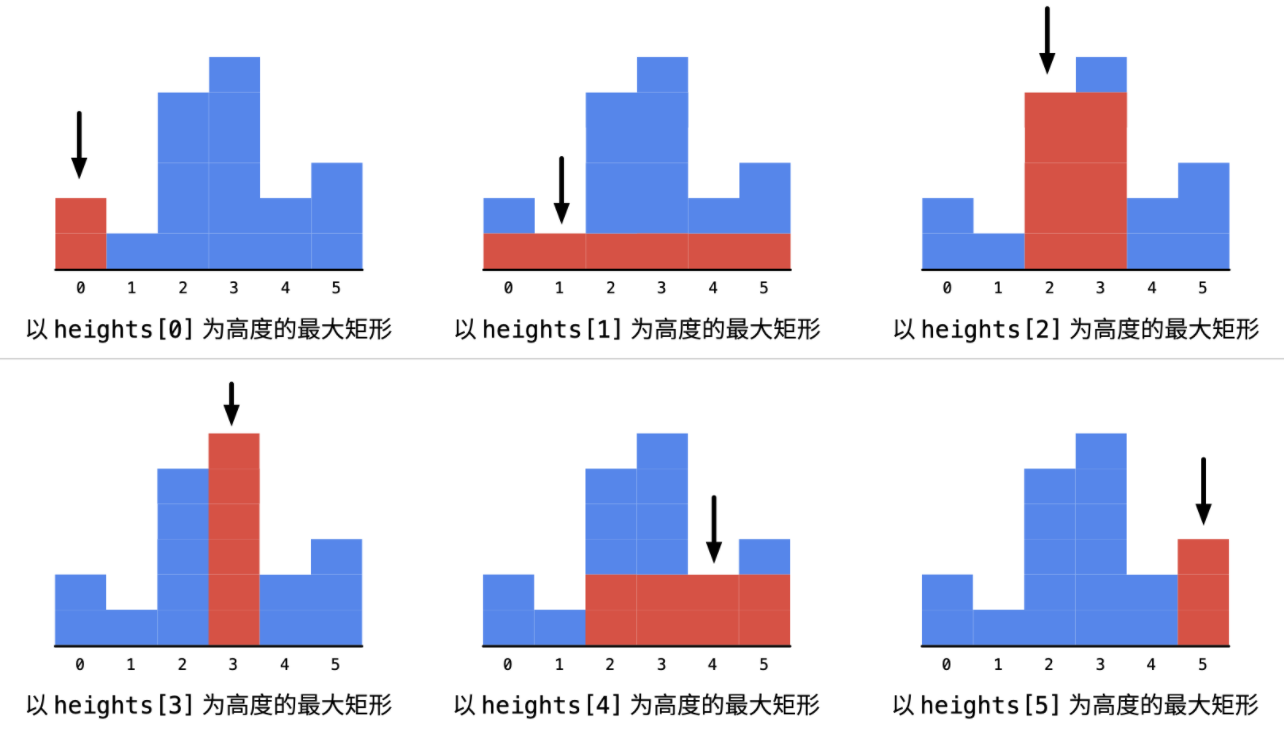
- 矩形面积 = 底 * 高,固定底求最大高度不好求,可以固定高求最长底边。从i向两边遍历,找到左边和右边第1个严格小于height[i]的时候停下,中间长度即是当前高度下最长底边。
- 依次遍历柱形的高度,对于每一个高度分别向两边扩散,求出以当前高度为矩形的最大宽度多少。
var largestRectangleArea = function (heights) {
let Square = 0; // 存放面积
for (let i = 0; i < heights.length; i++) {
// 寻找左扩展边界 左边第一个 小于 hieghts[i]的下标 的上一个
let expandLeft = i;
while (expandLeft > 0 && heights[expandLeft - 1] >= heights[i]) expandLeft--;
// 寻找右扩展边界 右边第一个 小于 heights[i]的下标 的上一个
let expandRight = i;
while (expandRight < heights.length - 1 && heights[expandRight + 1] >= heights[i]) expandRight++;
Square = Math.max(Square, heights[i] * (expandRight - expandLeft + 1));
}
return Square;
};
时间复杂度:O(n^2),n是数组 height 的长度,需要遍历一次数组,在每一个位置向两边扩散,每一次扩散最坏情况需要看完整个数组。
空间复杂度:O(1),使用常数个临时变量。
单调栈 (处理实参)
- 末尾添加一个元素,代表高度为0,避免栈中还有值时错过最大面积(处理全部单调递增 或 栈中有值的情况)
- 维护一个单调递增栈,当遇到 小于(小于等于也行) 栈顶元素时,进行弹栈,此时有 当高度为弹栈元素时 当前元素即使右扩展边界 栈顶元素为左扩展边界
- 即 弹栈元素为高计算举行面积 高为:弹栈元素,底为:当前元素下标 - 栈顶元素下标(栈中无元素即为-1) - 1
var largestRectangleArea = function (heights) {
heights.push(0); // 避免栈中还有值时错过最大面积(处理全部单调递增 或 栈中有值的情况)
const stack = []; // 单调递增栈
let Square = 0; // 存储面积
for (let i = 0; i < heights.length; i++) {
// 栈中有值 且 当前元素 小于(小于等于也行) 栈顶元素时有 当高度为弹栈元素 当前元素即使右扩展边界 栈顶元素为左扩展边界
while (stack.length && heights[i] < heights[stack[stack.length - 1]]) {
let middle = stack.pop();
// 如果栈中无值 则left为-1 有值为栈顶下标
let left = stack.length ? stack[stack.length - 1] : -1
let curSquare = heights[middle] * (i - left - 1);
Square = Math.max(Square, curSquare);
}
// 压栈
stack.push(i);
}
return Square;
}
时间复杂度:O(n),n为数组 heights 的长度,每一个元素入栈一次,出栈一次
空间复杂度:O(n),n为使用栈的最大保存容量,最多为数组 heights 的长度
单调栈 + 哨兵技巧
使用 「哨兵」 (Sentinel),避免特殊情况的讨论
哨兵1 解决栈为非空的判断
哨兵2 解决栈中所有元素都单调递增的情况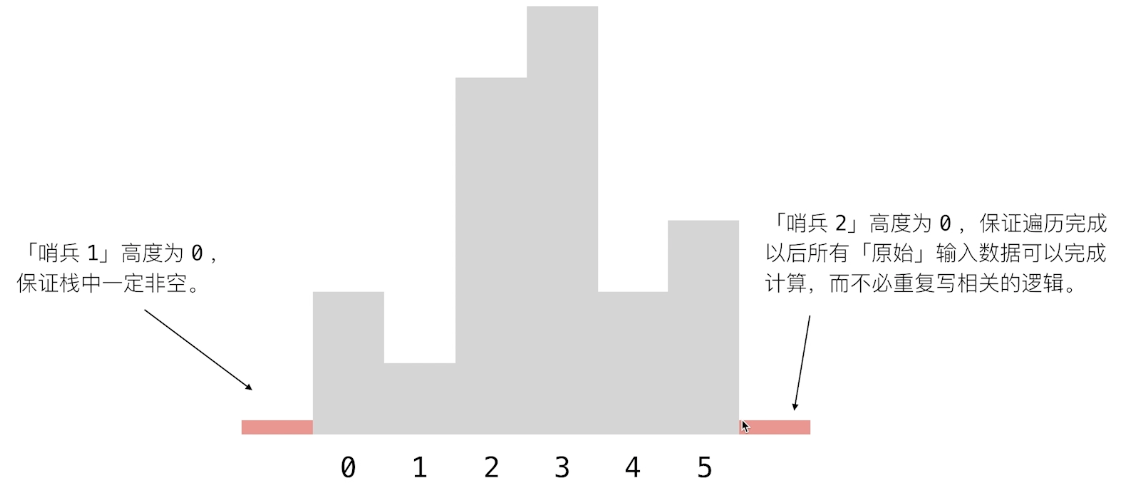
var largestRectangleArea = function (heights) {
const stack = []; // 单调递增栈
let Square = 0; // 存储面积
let newHeights = [0, ...heights, 0]; // 添加两个哨兵
for (let i = 0; i < newHeights.length; i++) {
// 栈中有值 且 当前元素 小于等于 栈顶元素时有 当高度为弹栈元素 当前元素即使右扩展边界 栈顶元素为左扩展边界
while (stack.length && newHeights[i] < newHeights[stack[stack.length - 1]]) {
let middle = stack.pop();
let curSquare = newHeights[middle] * (i - stack[stack.length - 1] - 1);
Square = Math.max(Square, curSquare);
}
// 压栈
stack.push(i);
}
return Square;
}
时间复杂度:O(n),n为数组 heights 的长度,每一个元素入栈一次,出栈一次
空间复杂度:O(n),n为使用栈的最大保存容量,最多为数组 heights 的长度
题目:LC42.接雨水
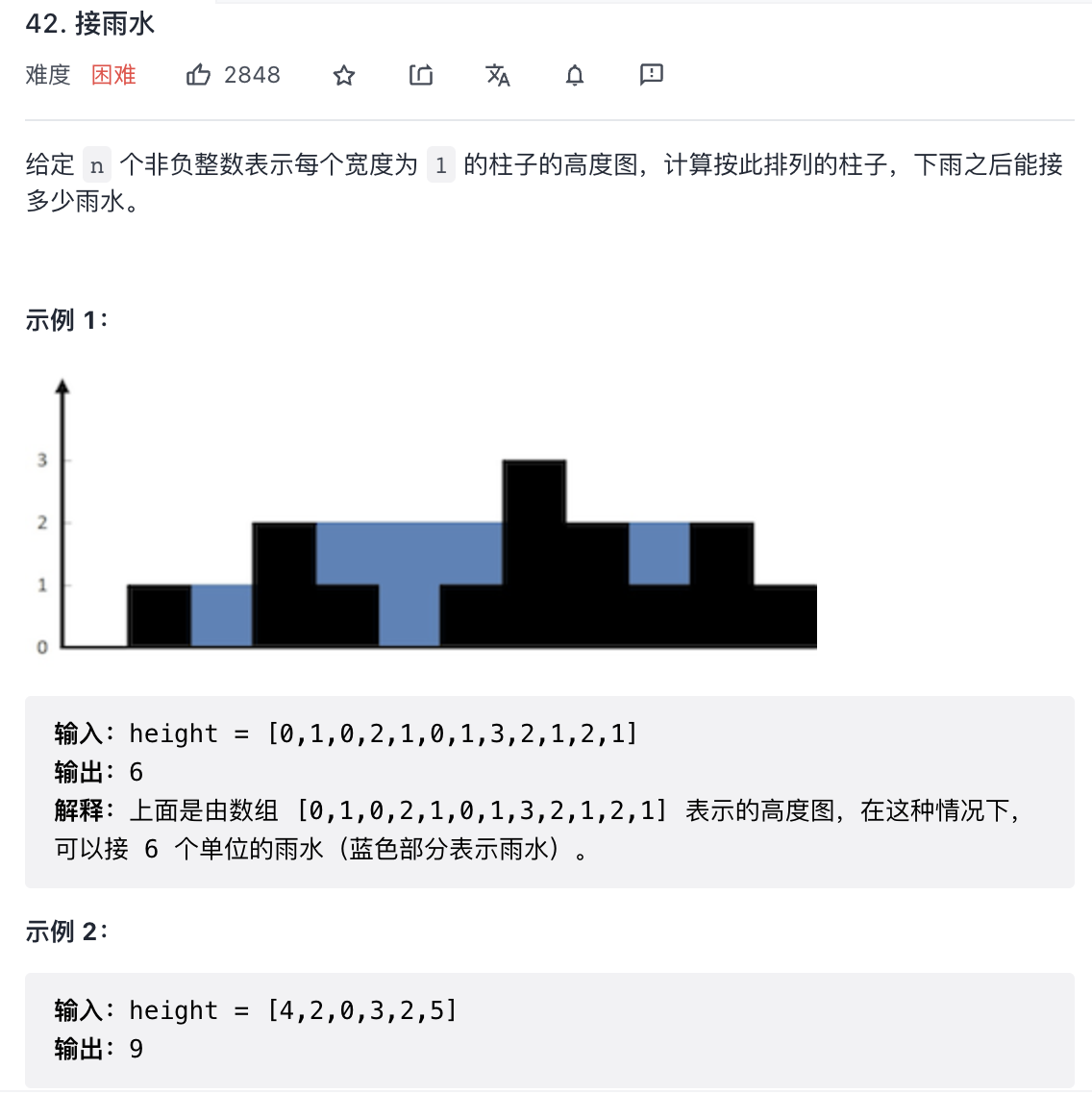
单调栈
维护一个单调递减栈,当遇到大于栈顶元素时,进行弹栈后栈中仍有值,此时形成了凹槽,左边有积水。
[0,1,0,2,1,0,1,3,2,1,2,1]
stack = [1,0] i=2
积水高度为:Math.min(当前元素高,栈顶元素高)-弹栈元素高
积水宽度为:当前索引-栈顶下标-1
宽度是 i-left-1,高度是 Math.mid(height[left],height[i])-height[top] 。
var trap = function (height) {
const stack = []; // 单调递减栈,当遇到大于栈顶的元素时候说明形成凹槽可以积累雨水,储存索引用于计算trap宽高
let sumTrap = 0; // 记录结果值 雨水面积
for (let i = 0; i < height.length; i++) {
// 栈中有值 且 当前元素 大于 栈顶元素 则弹栈
while (stack.length && height[i] > height[stack[stack.length - 1]]) {
let mid = height[stack.pop()];
if (stack.length === 0) break; // 弹栈后 如果栈为空 则没有trap无法积累雨水 结束本次循环;
// 弹栈后 如果栈中有值 则栈顶元素、弹栈元素、当前元素形成trap 计算积雨量
// 有 trap 底宽为:i-栈顶-1 高为:Math.mid(栈顶元素高,当前元素高)-弹栈元素高
sumTrap += (i - stack[stack.length - 1] - 1) * (Math.min(height[i], height[stack[stack.length - 1]]) - mid);
}
// 压栈
stack.push(i);
}
return sumTrap;
};
时间复杂度:O(n),n是数组 height 的长度。从0到n-1的每一个下标最多只会入栈出栈各一次。
单次遍历O(n),每个条形块最多访问两次(入栈和出栈),并且入栈和出栈都是O(1)的。
空间复杂度:O(n),n是数组 height 的长度。空间复杂度主要取决于栈空间,栈的大小不会超过n,最多在阶梯型或平坦型条形块结构中占用O(n)的空间。
题目:LC402.移掉k位数字

单调栈(删除数组高位的大数)
提示:对于两个相同长度的数字序列,最左边不同的数字决定了这两个数字的大小
例如,对于 A = 1axxx,B = 1bxxx,如果 a > b 则 A > B。
基于此,我们可以知道,若要使得剩下的数字最小,需要保证靠前的数字尽可能小。
从左到右遍历num数组,维护一个单调递增的栈,但遇到当前元素小于栈顶的元素时,进行弹栈,因为,栈顶的数在高位,删掉它,小的顶上,高位变小,整个数变小。
特殊情况:
- 如果我们删除了 m 个数字且 m < k,这种情况下我们需要从序列尾部删除额外的 k−m 个数字
- 如果最终的数字序列存在前导零,我们要删去前导零
- 如果最终数字序列为空,我们应该返回 ‘0’
var removeKdigits = function (num, k) {
const stack = []; // 单调递增栈
for (let i = 0; i < num.length; i++) {
// 栈中有值 且 当前元素 大于 栈顶元素 弹栈(弹栈元素不得超过k个)
while (k > 0 && stack.length && num[i] < stack[stack.length - 1]) {
stack.pop(); // 栈顶元素为位于高位的大数,应删除小树顶上
k--; // 记录删除个数
}
stack.push(num[i]);
}
for (; k > 0; k--) {
stack.pop();
}
// 处理结果
// 栈中无值,返回 0
// 栈底元素为0,将其删除
while (stack.length && stack[0] === '0') {
stack.shift();
}
return stack.length ? stack.join('') : '0';
}
时间复杂度:O(n),其中 n 为字符串的长度。尽管存在嵌套循环,但内部循环最多运行 k 次。由于 0 < k ≤ n,主循环的时间复杂度被限制在 2n 以内。对于主循环之外的逻辑,它们的时间复杂度是 O(n),因此总时间复杂度为 O(n)。
空间复杂度:O(n),栈存储数字需要线性的空间。

