幂的运算：X的n次幂

计算X的n次幂，有多种算法
例子：计算2的62次方。
method 1 ：time = 2099 纳秒。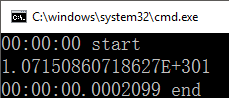

常规思路，进行61次的乘法！

 Stopwatch sw = new Stopwatch();
 Console.WriteLine($"{sw.Elapsed} start");
 sw.Start();
 Console.WriteLine(Math.Pow(2,62));
 sw.Stop();

method 2 ：time = 113 纳秒
进行拆分：2^62 = (2^31)^2 = (2^31)(2^31) // 得到 2^31 的值的情况下，需要 1 次乘法
　　　　　2^31 = (2^15)^22 = (2^15)(2^15)2 // 得到 2^15 的值的情况下，需要 2 次乘法
　　　　 2^15 = (2^7)^22 = (2^7)(2^7)2 // 得到 2^7 的值的情况下，需要 2 次乘法
　　　　 2^7 = (2^3)^22 = (2^3)(2^3)2 // 得到2^3 的值的情况下，需要 2 次乘法　
　　　　　2^3 = 222 　　　　　　　　　　 // …………………………，需要2次乘法
所以：该方法需 2+2+2+2+1 = 9 次乘法！

class Program
{
    static void Main(string[] args)
    {
        Stopwatch sw = new Stopwatch();
        Console.WriteLine($"{sw.Elapsed} start");
        sw.Start();
        Console.WriteLine(Math.Pow(2,1000));
        sw.Stop();
        Console.WriteLine($"{sw.Elapsed} end");
        sw.Restart();
        pow(2, 1000);
        Console.WriteLine(sw.Elapsed);
        Console.ReadKey();
    }
    public static long pow(long x, long n)
    {
        if (n == 0)
        {
            return 1;
        }
        // 如果是偶数
        if (isEven(n))
        {
            return pow(x * x, n / 2);
        }
        else
        {
            return pow(x * x, n / 2) * x;
        }
    }
    private static Boolean isEven(long x)
    {
        if (x % 2 == 0)
        {
            return true;
        }
        if (x % 2 == 1)
        {
            return false;
        }
        return false;
    }
}